基于随机响应面法的结构可靠度敏感性分析理论及其工程应用
季 昀,段 杭,孟亚运,王 霄,李同春
(1.国家能源局大坝安全监察中心,浙江 杭州 310014;2.中国电建集团华东勘测设计研究院有限公司,浙江 杭州 310014;3.中国三峡建工(集团)有限公司白鹤滩工程建设部,四川 成都 610041;4.中国电建集团中南勘测设计研究院有限公司,湖南 长沙 410014;5.淮安市水利勘测设计研究院有限公司,江苏 淮安 223001;6.河海大学水利水电学院,江苏 南京 210024)
0 引 言
结构可靠度敏感性分析,或称为结构可靠度灵敏度分析,是结构可靠度分析的重要组成部分。通过结构可靠度敏感性分析,可以得到各输入随机变量分布参数的变化引起失效概率变化的不同程度,从而确定各参数对结构安全影响的重要程度,为工程设计、施工和管理供有益的指导与反馈。
依据结构可靠度敏感性分析的定义,不难得到一次二阶矩法等结构可靠度算法所对应的敏感性分析公式。然而,由于一次二阶矩等方法仅适用于功能函数为显式的情况,而重力坝等复杂结构的可靠度分析功能函数通常为隐式函数,此时,基于一次二阶矩法的结构可靠度敏感性分析公式将不再适用。作为一种新兴的代理模型方法(Metamodel,Model of model),随机响应面法采用随机多项式[1](一般为Hermite正交多项式)作为响应面函数,相比于经典响应面法所采用的序列多项式,具有明确的数学意义和理论证明的收敛特性[2]。近年来,随机响应面法及基于随机响应面法的非侵入式随机有限元法在工程结构可靠度分析中得到了一定的推广和应用[3-7]。然而,目前尚未出现有关结构可靠度随机响应面法敏感性分析及其应用方面的文献。Sudret[8]采用随机多项式进行了系统敏感性分析,但其研究的对象是物理系统,且对应的敏感性分析研究本质上属于方差分析的范畴,与结构可靠度敏感性分析的定义并不相同。Isukapalli[9]在其博士论文中研究了“Coupling of the SRSM with sensitivity analysis methods”,并编写了相关计算程序SRSM-ADIFOR。但是,Isukapalli的研究仅仅是得到了随机响应面方程对于各随机变量的偏导公式,而结构可靠度敏感性分析真正需要求解的应是失效概率对于各随机变量及其特征参数的偏导公式。
一般地,由于随机响应面法的基本变量均为标准正态随机变量,故可以将随机响应面法与几何法结合起来求解结构可靠指标和失效概率。本文将推导几何法与随机响应面法相结合的结构可靠度敏感性分析公式,并应用于工程实例。
1 基于一次二阶矩方法的结构可靠度敏感性分析
一次二阶矩法在均值点将功能函数进行展开,在应用时具有诸多的局限性[10]。但是,作为最早出现的结构可靠度计算方法,该方法概念清晰,便于阐述结构可靠度敏感性分析的概念。因此,在介绍基于随机响应面法的结构可靠度敏感性分析理论前,首先给出基于一次二阶矩方法的结构可靠度敏感性分析计算公式及其推导过程。
一般情况下,可以认为失效概率与可靠指标具有如下一一对应的关系
Pf=1-Φ(β)
(1)
式中,Pf为失效概率;Φ(·)为标准正态分布的累积概率分布函数;β为可靠指标。
由式(1),可得

(2)
式中,φ(·)为标准正态分布的概率密度函数;其他各变量含义同前。
当输入基本随机变量向量x相互独立且功能函数为线性时,有
(3)
(4)
式中,μxi为输入随机变量xi的均值;ai为线性功能函数g的表达式中xi所对应的系数;σg为功能函数g的标准差。则失效概率Pf对于均值μxi和标准差σxi的敏感性可表示为
(5)
(6)
当基本随机变量向量x中各变量相互独立且功能函数为非线性时,可得失效概率Pf对于均值μxi和标准差σxi的敏感性为
(7)
(8)
2 基于随机响应面法的结构可靠度敏感性分析
随机响应面法是一种全局响应面法,因而基于该方法的敏感性分析是具有实际物理意义的,而以经典响应面法(序列多项式响应面法)为代表的局部响应面法通常并不具有这样的特性。此外随机响应面法的基本变量均为标准正态随机变量,可以方便地将随机响应面法与几何法结合起来求解结构可靠指标和失效概率。
对任意设计变量b(可以代表任一随机变量的均值或标准差),结构的失效概率对其敏感性可表述为
(9)
式中,b为任意设计变量;其余各符号含义同前。
当在结构可靠度随机响应面法中采用几何法计算结构的可靠指标时,可靠指标的求解可等效表述为几何法中的约束问题。当分析结构失效概率对设计变量b的敏感性时,有

(10)
式中,ξ为结构的输入随机变量向量为输入变量向量x经一定的变量转换运算得到一组新的标准正态随机空间内的随机变量向量,且ξ=(x-μx)/σx={ξ1,ξ2,…,ξn}T;其他各符号含义同前。

δβ=∇ξL(ξ)δξ
(11)
式中,δβ为可靠指标β相对于变量b的变分;δξ为输入随机变量向量ξ相对于变量b的变分;L(ξ)=(ξTξ)1/2;∇ξL(ξ)表示L(ξ)对于正态分布的随机向量ξ的矢量导数。

δg=∇bgδb+∇ξgδξ=0
(12)
式中,∇bg为极限状态方程g在点ξ*和b0处对不同取值的变量b构成的向量b的矢量导数;∇ξg为极限状态方程g在点ξ*和b0处对输入随机向量ξ的矢量导数。
根据非线性规划的相关理论,上式须在b*处满足Kuhn-Tucker条件,而这可以通过引入拉格朗日乘子λ来实现。于是,式(10)所示的约束问题最终转化为
∇ξL(ξ)+λ∇ξg(ξ)=0
Subject toZ=g(ξ*,b0)=0
(13)
由式(12),易得
∇bgδb=-∇ξgδξ
(14)
将式(14)代入式(13),可得
∇ξLδξ=λ∇bgδb
(15)
综上,可靠指标对于任意变量b的敏感性可表示为
(16)
式(16)中的拉格朗日乘子λ可以由Kuhn-Tucker条件∇ξL(ξ)+λ∇ξg(ξ)=0求得。对该方程两边同取欧式范数(2-范数),有

(17)

由于拉格朗日乘子λ为负实数,因此有
(18)
当上述推导过程中的变量b表示为任一输入随机变量ξi(i=1,2,…,n)的均值时,有
(19)
(20)
故可靠指标β对于输入随机变量向量的均值的敏感性计算公式可表示为
(21)
同理,若将变量b表示为任一输入随机变量ξi(i=1,2,…,n)的标准差时,类似可得
(22)
式(21)、式(22)与式(3)、式(4)在形式上是一致的,这表明,式(3)、式(4)为式(21)、式(22)的一种特殊形式。类似地,可得采用几何法的结构可靠度随机响应面中失效概率Pf对于均值μxi和标准差σxi的敏感性计算公式为
(23)
(24)
显然,式(23)与式(24)结果均为无量纲的数值,可以用于衡量失效概率对于不同输入随机变量的敏感性。如用随机响应面函数替代式(23)和式(24)中的极限状态方程g,即得到几何法与随机响应法相结合的结构可靠度算法的敏感性分析公式。
3 算例验证及工程应用
3.1 算例——非线性方程
(25)
式中,ξ1、ξ2均为标准正态随机变量,分别由结构输入随机变量x1、x2转化而来。
令ξ={ξ1,ξ2},x={x1,x2},则有
(26)
式中,μx为输入随机变量向量x的均值向量,且μx={1 000,250};μx为输入随机向量x的标准差向量,且σx={200,37.5}。
可以认为,随机响应面法拟合得到的功能函数即为结构实际的功能函数。则求得结构功能函数分别对各基本变量ξi(i=1,2)的偏导表达式如下

(27)
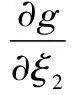
(28)
采用几何法求得标准正态空间内的设计验算点为ξ={ξ1,ξ2}={0.625 6,-2.244 9},将其代入式(27)和式(28),分别得到在设计验算点附近结构功能函数对各基本随机变量ξi(i=1,2)的偏导数分别为-3.103和6.596 3。
于是,不难得到结构功能函数对输入随机变量的2-范数为
(29)
根据前述推导得到的采用几何法的结构可靠度随机响应面敏感性分析公式,求得结构失效概率对各输入随机变量的均值敏感度如式(30)和式(31)所示,对标准差的敏感度如式(32)和式(33)所示。
(30)
(31)
(32)
(33)
由式(30)和式(31)可见,在设计验算点附近,结构失效概率将随着输入随机变量x1均值的增加而增大,随着输入随机变量x2均值的增加而减小;当随机变量x1和x2的标准差增加(或称随机变量的变异系数增加)时,结构的失效概率都会增加。
由文献[11]中对输入随机变量x1和x2的描述可知,x1为悬臂梁所受荷载,x2为悬臂梁的截面尺寸。由此可以认为,该悬臂梁的结构失效概率将随着荷载均值的增加而增大,随着截面尺寸均值的增加而减小,符合工程经验认识。同时,荷载与截面尺寸的标准差的增大(或称变异系数的增大)将导致结构失效概率的增大,也即结构可靠指标减小。
3.2 工程应用——重力坝
某水电站位于柬埔寨的Kamchay河干流,挡水建筑物为混凝土重力坝,最大坝高112 m,坝顶宽6.0 m,坝体上游面84m高程以上为竖直面以下坡度为1∶0.3;下游面折坡点高程为145.00 m,折坡点以下坡度为1∶0.75。
选取最大坝高断面(5号坝段)进行分析,该坝段建基面高程为41 m,坝顶高程为153 m,坝底宽97 m,上游正常蓄水位150 m。建立该坝段的二维有限元分析网格模型,坝基在上下游方向各延伸200 m,坝基深度取为200 m,有限元网格模型如图1所示。根据坝体混凝土所采用的型号,坝体弹性模量取值范围为21.5~25.5 GPa;试验得到的坝基岩体弹性模量取值范围为3~8 GPa。利用实测位移监测数据对其进行反演分析后,得到该坝段的坝体弹性模量均值为21.88 GPa,坝基弹性模量均值为4.64 GPa。参考类似工程,假定坝体弹模Ec、坝基弹模Er及大坝上游水位Hu3个随机变量的变异系数分别取为0.15、0.20、0.06,如表1所示。

图1 重力坝有限元网格模型

表1 各随机变量统计特性
采用非侵入式随机有限元法(随机响应面法+有限元法)进行结构可靠度分析时的计算流程如图2所示。

图2 基于非侵入式随机有限元法的结构可靠度随机响应面法计算流程
根据图2所示的计算流程,首先,建立本实例的重力坝坝踵抗拉可靠度功能函数为
Z=g(x)=g(Hu,Ec,Er)=6.79-wt
(34)
式中,x为输入随机变量向量;wt为重力坝坝踵的拉应力区宽度,m。
与式(34)意义类似,如果坝踵的拉应力区是连续的,可以以坝基面上距离坝踵6.79 m处的垂直向应力σy的正负来形成重力坝的抗拉功能函数
Z=g(x)=-σy
(35)
式中,σy为坝基面上距离坝踵7/100坝底宽度处的垂直向应力,应力符号以拉为正,以压为负。
显然,由于引入了有限元分析,得wt到关于输入随机变量向量x的显式表达式是比较困难的,因此,式(34)与式(35)所示的功能函数均为隐式方程。
将输入的非标准正态分布随机变量向量x=(x1,x2,x3)转换为服从N(0,12)的标准正态随机向量ξ=(ξ1,ξ2,ξ3),其中,x1代表大坝上游水位Hu;x2代表坝体弹性模量Ec;x3代表坝基弹性模量Er。
应用自编结构可靠度随机响应面法程序,得到重力坝抗拉可靠度的二阶随机响应面函数如式(36)所示。经验算,二阶随机响应面函数和三阶随机响应面函数精度相差较小,故选择二阶随机响应面函数用于重力坝结构抗拉可靠度计算是合适的。
(36)
以式(36)作为重力坝结构抗拉可靠度的功能函数,应用几何法求得重力坝抗拉可靠指标为1.629,对应的失效概率为5.17%。标准正态空间的设计验算点为[-0.765,-0.387,-1.385],将其转换至原始变量空间为[143.115 m,20.609 GPa,3.355 GPa]。
求得结构功能函数分别对各基本变量ξi(i=1,2,3)的偏导
(37)
(38)
(39)
采用几何法,得到标准正态空间内的设计验算点为ξ=(-0.765,-0.387,-1.385),将其代入式(37)~式(39),得到在设计验算点附近结构功能函数分别对各基本变量ξi(i-1,2,3)的偏导数依次为89.573 1、45.247 0和161.992 3。
于是,不难得到结构功能函数对输入变量向量偏导的2-范数为
(40)
根据前述推导得到的采用几何法的结构可靠度随机响应面敏感性分析公式,求得结构失效概率对各输入随机变量的均值敏感度如式(41)~式(43)所示,对标准差的敏感度如式(44)~式(46)所示。
(41)
(42)
(43)
(44)
(45)
(46)
分析式(41)~(43)可知,在设计验算点处,该重力坝的结构抗拉失效概率对于各输入随机变量均值的敏感性排序为:坝基弹性模量Er>坝体弹性模量Ec>大坝上游水位Hu。同时,结构抗拉失效概率对于各输入随机变量均值的敏感度均为负值,这说明在设计验算点处,坝基弹性模量越大、坝体弹性模量越大或大坝上游水位越高(设计验算点处的上游水位为143.115 m,低于正常蓄水位150 m)都将降低结构的抗拉失效概率。
分析式(44)~(46)可知,在设计验算点处,该重力坝的结构抗拉功能函数对于各输入随机变量标准差的敏感性排序为:坝基弹性模量Er>大坝上游水位Hu>坝体弹性模量Ec。同时,结构抗拉失效概率对于各输入随机变量标准差的敏感度均为正值,这说明在设计验算点处,坝基弹性模量变异越大、坝体弹性模量变异越大或大坝上游水位波动越大都将增加结构的抗拉失效概率。
综上所述,坝基弹性模量的均值与标准差对其抗拉可靠度最为敏感。因此,建议通过补强灌浆等方式提高坝基的弹性模量,可以显著提高该重力坝结构抗拉可靠指标。
4 结 论
本文推导了几何法与随机响应面法相结合的结构可靠度敏感性分析公式,并应用于工程实例,得到了相关结论。研究表明:
(1)本文给出的基于随机响应面法和几何法的结构可靠度敏感性分析公式可有效分析和比较失效概率和可靠指标对于各随机变量的敏感程度。
(2)将本文给出的计算公式应用于悬臂梁和某重力坝结构可靠度分析的实例,收到了良好的效果,得到了有益的结论。对于该重力坝,坝基弹性模量的均值与标准差对其抗拉可靠度最为敏感。因此,本文建议通过补强灌浆等方式提高坝基的弹性模量,可显著提高其坝踵抗拉可靠指标。

