基于小波包分频的自适应模糊神经网络风电功率平抑策略

刘树伟，李 欣，王 红，韩 伟，胡 月，张海宁，张宇宁

(1.河北民族师范学院物理与电子工程学院，河北 承德 067000；2.国网冀北电力有限公司承德公司，河北 承德 067000；3.国网冀北电力有限公司北京超高压公司，北京 102488)

0 引 言

近年来国家对碳中和的高度重视使得新能源得到快速发展，其中高比例的风力发电装机持续增加，受风速波动影响较大风电出力更是难以调控，这给并网发电时的电网的调度带来一定困难，今后很长一段时间也将严重制约风力发电的开发与利用规模，实现精准跟踪调度指令，减小风电出力波动对电网的影响是专家学者研究的热点课题[1-2]。尽量减小风力发电的随机性和间歇性给电网调度带来的调度困难，配备合适容量的混合储能是提高电网系统的稳定性考虑最多的。采用循环寿命长、功率密度和能量密度高、环保节约的混合储能以超级电容与蓄电池的应用最为广泛[3-4]。对于目前的混合储能的控制策略，为得到储能系统补偿功率和目标并网功率，有学者采用滑动平均算法或低通滤波算法，此方法容易造成电池的过充过放，影响电池的寿命是由于算法未考虑电池荷电状态的变化的影响[5-8]，为完成对储能设备荷电状态的实时调节，有专家学者在滑动平均算法或低通滤波算法控制策略的基础上加入模糊控制算法，此方法中的模糊控制费时费力，是因为对隶属函数和模糊规则的调整困难，在采用经验值计算时的自学习、自组织、自适应功能功能弱[9-11]。将表达能力、推理能力较强的Sugeno型模糊模型和神经网络结合可以有效提高控制效果，但在功率分频上存在不足[12-15]，而小波包分解分频原理在传统小波包分解的基础上，使得分解结果既可以满足并网标准，也可以减少储能冗余容量。因此将自适应小波包分解分频原理与模糊神经网络结合建立自适应小波包分频的模糊神经网络系统可对混合储能控制系统进行优化，MATLAB/simulink仿真结果表明在配有混合储能的风电出力跟踪调度指令偏差小，频率波动小，混合储能电池充放电均衡。

1 风储系统

1.1 风储系统模型

风储系统模型如图1所示。此系统混合储能由功率型电池超级电容和能量型电池磷酸铁锂电池组成，将对风电功率分解数据经控制系统后发送给混合储能设备协调指令，对风电场输出功率进行波动平抑，使风电场发电功率满足并网标准，完成风电平滑并网任务。

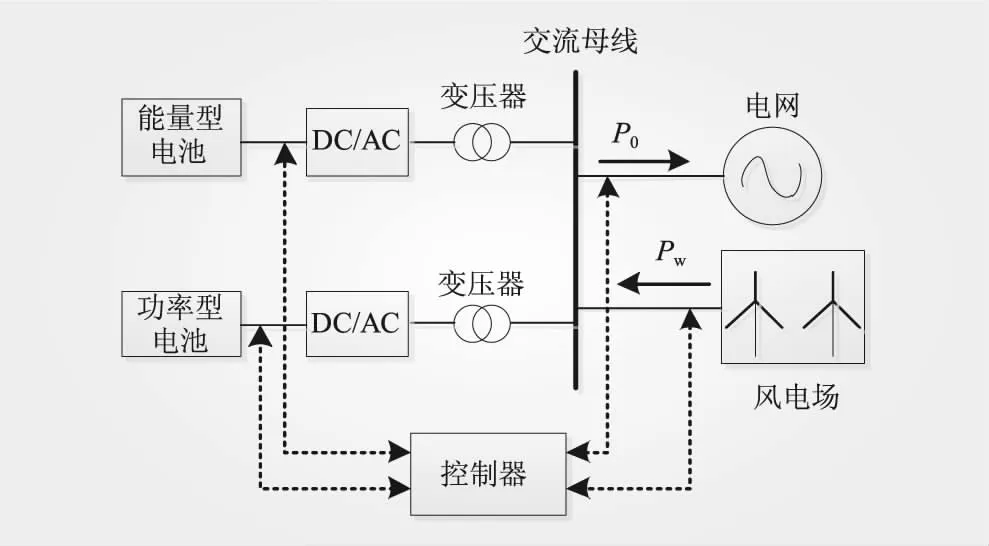
图1 风储系统模型

1.2 风储系统约束

依据混合储能设备的工作状态得出储能剩余容量，将剩余储能容量与储能设备SOC(荷电状态)值建立模型，得到储能设备SOC值为

(1)

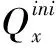
从安全和使用寿命两方面进行考虑，同时考虑混合储能设备平滑下一刻风电出力的能力，应保证混合储能设备荷电状态值在其允许范围内，需满足

(2)

式中，Sx.min和Sx.max分别为储能设备的最小和最大荷电状态值；Px.min和Px.max分别为储能设备充放电功率的上、下限制。

2 自适应小波包分频方法

2.1 小波包分频原理

自适应小波包分解分频原理在传统小波包分解的基础上，对风功率进行分解，得出高、中、低频信号，同时采用并网标准确定小波包分解层数，使得分解结果既可以满足并网标准，也可以减少储能冗余容量。自适应小波包分解架构如图2所示。

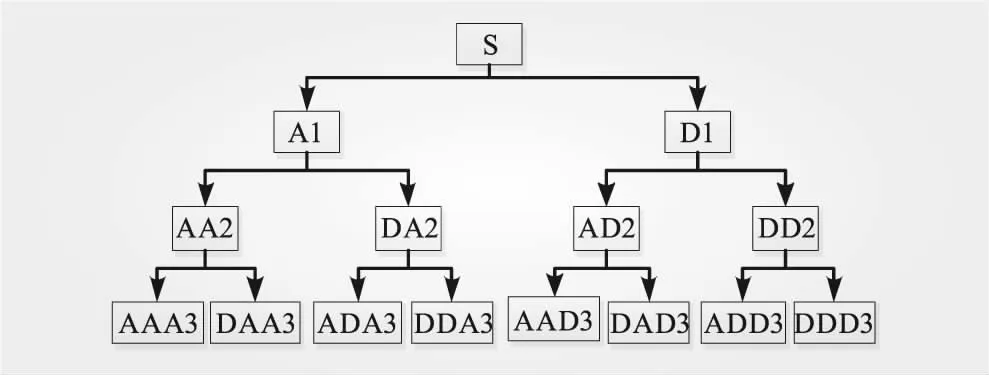
图2 自适应小波包分解

风电输出功率为Pw(t)，对风电功率进行小波包分解，模型为

(3)

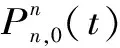
(4)

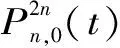
2.2 风电功率自适应小波包分解

传统小波包分解需提前设定分解层数n，设定分解层数n具有主观性，不合适的n值则会导致欠分解和过分解的问题，因此本文提出自适应模糊神经网络的小波包分解算法，可自主确定最佳分解层数n保证分解结果的精度。依据风电分解标准，设定t时刻风电并网功率Pout(t)，对应分解的10 min功率变化范围为

(5)

1 min功率变化范围为

(6)

则风电实际并网功率Pout(t)满足并网标准区间[Pmin(t)，Pmax(t)]，即

Pout∈[Pmin，Pmax]=[P1，min，P1，max]∩[P10，min，P10，max]

(7)

2.3 混合储能系统功率分配

依据混合储能设备的差异特性，使用自适应模糊神经网络小波包分频，得到低、中、高3种形式信号，其中低频信号波动平缓符合并网标准作为并网实际功率，中频信号特性与能量型储能设备特性相似，因此锂电池组吸收中频信号，超级电容则吸收高频信号。

假设风电总出力为Pw(t)，并网功率为Pout(t)，混合储能设备功率PHESS(t)为能量储能装置输出功率Pb(t)与超级电容输出功率Psc(t)之和。自适应小波包分解后各信号的关系为

(8)

式中，对风电Pw进行N层分解，其中P1为低频信号，Ph1～Ph2为中频信号，Ph3～Ph(2N-1)为高频信号。

3 模糊规则

筛选和整理出有代表性的风电场50组历史实测数据组如式(9)所示。

(9)

式中，p1为风电出力跟踪调度指令偏差值历史实测数据；soc为风电场混合储能荷电状态平均值历史实测数据；p2为风电场送给混合储能的功率指标历史实测数据；n为风电场历史实测数据的组数。

根据这50组数据组归纳总结出初始模糊规则的步骤如下：

(1)根据风电场50组历史实测数据组确定模糊论域。

(2)根据风电场50组历史实测数据组构建模糊规则。

(3)根据风电场50组历史实测数据组“留大去小”原则决定模糊规则强度。

(4)根据风电场50组历史实测数据组确定模糊规则表，模糊子集均为5个的两输入单输出，表1为组成的25条模糊规则。

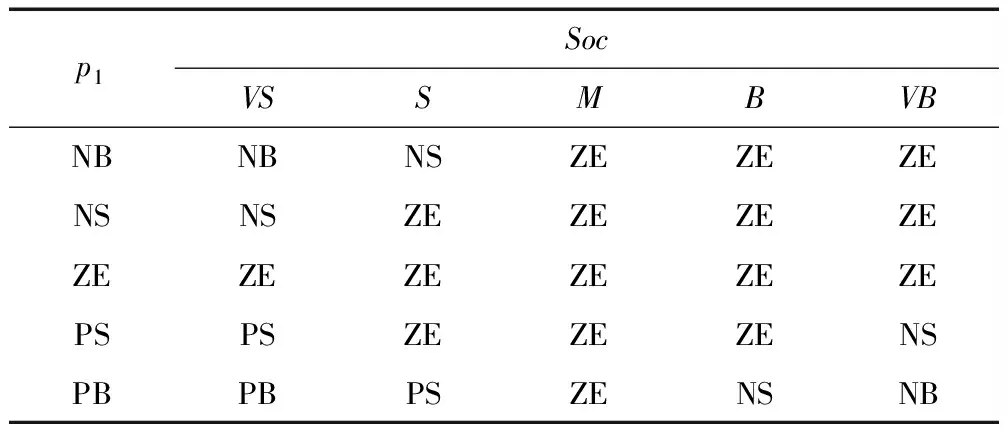
表1 模糊规则

4 小波包分频模糊神经网络

依靠人工归纳总结建立的上述风电场实测数据生成的初始模糊规则属于Madani型模糊控制系统，以下是采用小波包分频自适应Sugeno型模糊神经网络的建立方法。

4.1 小波包分频下的储能

采用两输入、单输出系统的小波包分频的模糊神经网络的模糊控制器输出的功率偏差采用低通滤波器将功率分为高频分量和低频分量，电池承担功率的低频分量，由超级电容负责高频分量，从频域转换到时域的滤波器传递函数计算过程为

(10)

式中，τ为滤波器传递函数中的滤波时间常数。

经t时间滤波后的电池和超级电容器的功率分别为

(11)

(12)

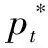
滤波时间常数为τ，与之相关的滤波系数λ取值范围为0～1，λ函数为

(13)

混合储能的能量分配经验表明滤波系数λ较大时降低负担功率，减小超级电容功率波动，增加电池输出功率。滤波系数λ较小时超级电容不利于承担波动较大的功率，这时输出的电池功率较为平滑。

4.2 模糊神经网络

采用5层前馈网络结构的自适应模糊神经网络的过程设计工作如下。

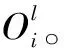
(14)

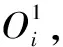
(15)

归一化层的第i个节点计算第i条规则的归一化可信度为输入层第三层，模糊规则数为该层节点数，第三层输入函数为

(16)

划分输出变量模糊度个数的是每个节点i，模糊规则输出层为输出第四层，节点i的输出函数如式(17)所示，该节点的参数集为pi，qi，ri。

(17)

将所有精确计算的输入信号转换为清晰的输出量，即清晰化层，也是第五层，公式为

(18)

图3是采用5层前馈的目前应用和研究最多的模糊神经网络结构。

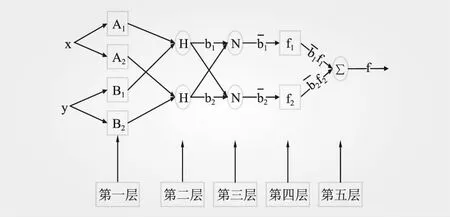
图3 模糊神经网络

4.3 小波包分频的模糊神经网络

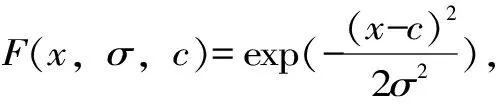
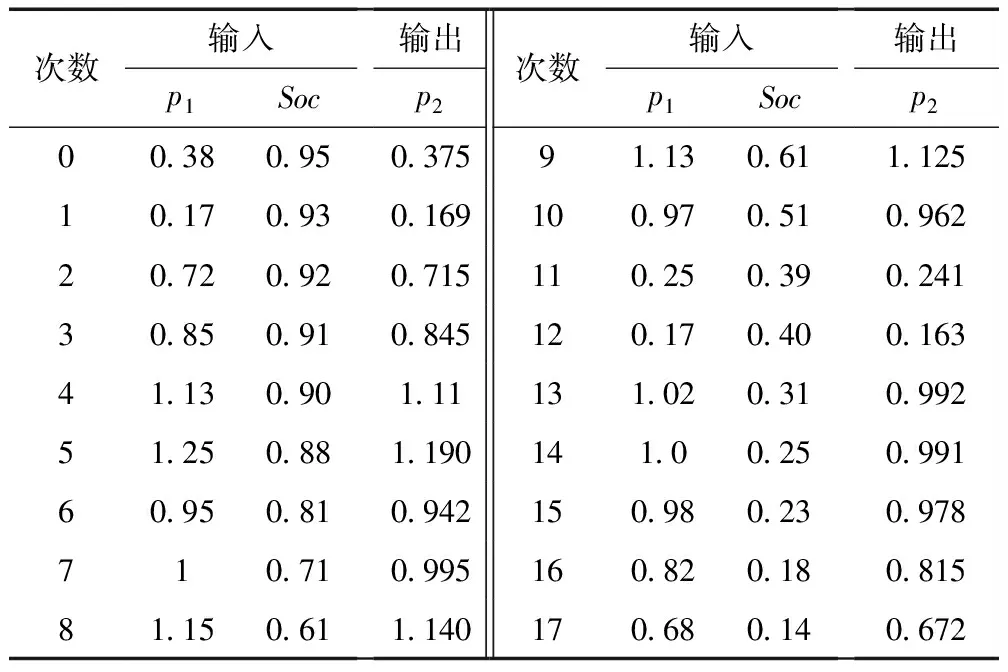
表2 小波包分频模糊数据

小波包分频模糊神经网络模糊的两个输入单个输出量会随自适应规则变化，如表2数据所示在得到两个历史给定输入量参数相同时，小波包分频模糊神经网络输入p1=0.38，soc=0.95，训练后的输出p2=0.375较之前的输出p2=0.36更准确。

5 仿 真

本文利用MATLAB/simulink对风混合储能系统建模仿真，风电场装机容量为49.5 MW，混合储能配置1 MW，储能参数配置如表3所示，风混合储能系统历史运行数据采用新疆阿拉泰某天一般风况数

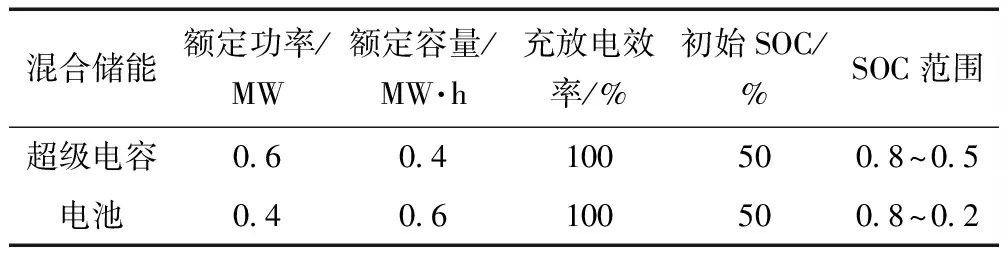
表3 储能参数

据，仿真数据由风电出力跟踪调度采样间隔时间共采样2万次的数据进行仿真，仿真结果表明自适应小波包分频模糊神经网络控制的有效性。

5.1 小波包分频的模糊神经网络仿真

图4为风电输出功率和风电并网功率曲线，可以看出实际的风储功率曲线与风电出力功率波动曲线由相同的波动趋势，功率波动可以达到1.2 MW，较大的功率会严重影响电网的频率进而对电网调度的调控带来很多挑战。

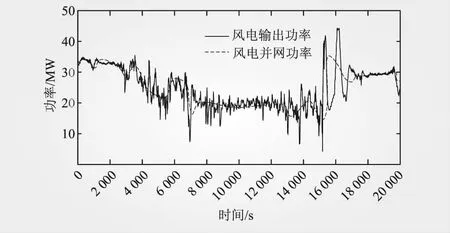
图4 风电出力和并网功率

图5为未加入优化控制策略的功率和加入优化控制策略的功率偏差波形图，仿真在0.9～1.6 s会出现偏差，其中最大偏差在1.15 s时为1.2 MW，功率偏差率达到总装机的2.42%，而加入优化控制后的功率偏差在±0.5 MW范围内波动，功率偏差率达到总装机的1.05%，可见加入优化控制后的跟踪调度指令功率偏差率降低一倍，波动更小。

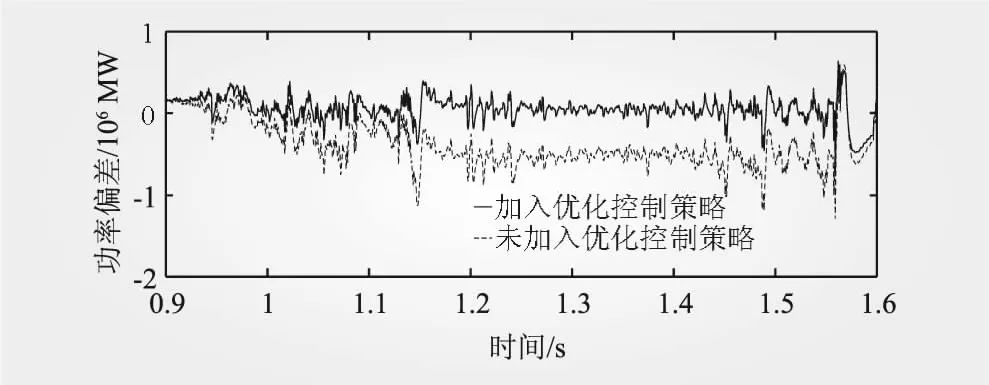
图5 加入优化控制策略前后的风储功率偏差波形

图6为未加入优化控制超级电容荷电状态和加入优化控制策略的超级电容荷电状态波形图，在仿真的0.8～1.8 s优化控制策略的荷电状态从之前的77%～60%之间波动恢复到75%～62%，波动率有17%降低到13%。图7为未加入优化控制电池荷电状态和加入优化控制策略的电池荷电状态波形图，在仿真的0.8～1.8 s优化控制策略的电池荷电状态均在90%～10%之间，但加入优化控制策略的电池荷电状态在1.6 s以后快速回归到60%，可见加入优化控制策略降低了4%的超级电容的荷电状态波动，超级电容和电池的充放电深度得到了效保护。

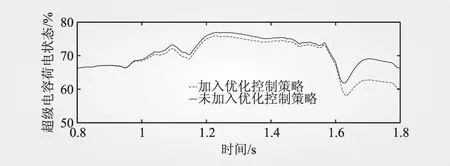
图6 加入优化控制策略前后的超级电容荷电状态波形

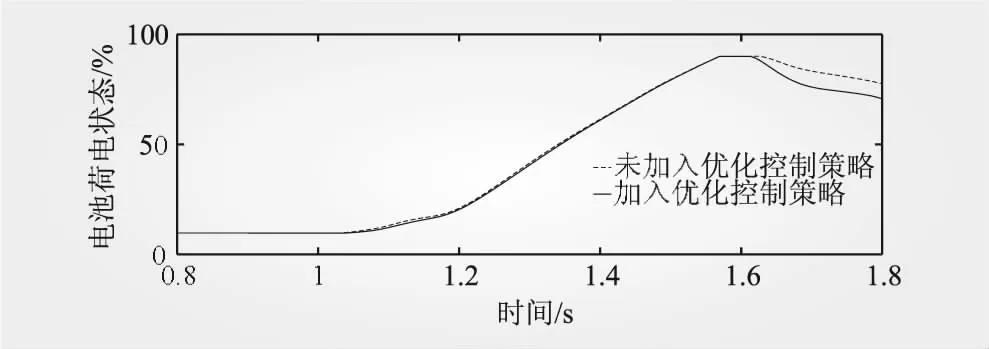
图7 加入优化控制策略前后的电池荷电状态波形

图8为未加入优化控制并网点频率波形图和加入优化控制策略的并网点频率波形图，仿真系统频率设置为50 Hz，并网点频率在49.9～50.6 Hz波动，在仿真的0.15～0.85 s出现明显偏差，加入优化控制策略后的频率在0.4～0.7 s之间波动频繁但是波动幅度较小，但较未加入优化控制策略时减小了0.1 Hz的频率波动，波动较小的频率更有利于风储系统并网较好的电能质量，对电网调度也会更加友善。

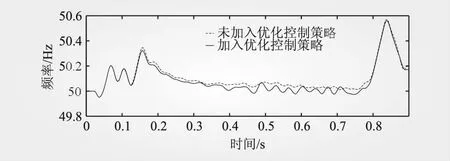
图8 加入优化控制前后的并网点频率波波形

表4为未加入优化控制和加入优化控制策略的储能误差指标对比，加入优化控制后的储能在平均绝对百分比误差较之前减小1.42%、最大百分比误差较之前减小1.2%、均方根误差较之前减小3.92%，仿真数据分析表明自适应小波包分频模糊神经网络控制的风电混合储电站的3个指标得到了明显的改进，使得风储电站跟踪电网调度的可靠性更高。

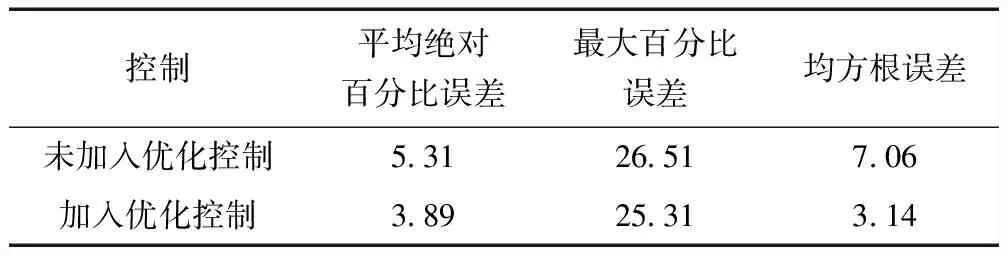
表4 加入优化控制前后的指标 %

6 结 语

采用自适应模糊神经网络的小波包分频优化控制策略在风电跟踪调度指令的频率波动范围内优化小波包分频参数，得到优化后的混合储能充放电功率的初始功率指标值，将混合储能荷电状态的平均值和风电场出力与电网调度指令的平均值的偏差作为两个输入，再将风电历史数据训练后的自适应小波包分频模糊神经网络加入控制系统。采用大量风电历史数据在MATLAB/simulink中仿真，仿真结果表明加入优化控制后的控制策略跟踪调度指令功率偏差率从2.42%降低到1.05%，超级电容的荷电状态波动降低了4%，频率波动减小了0.1 Hz，平均绝对百分比误差减小1.42%、最大百分比误差减小1.2%、均方根误差减小3.92%，这些数据表明该策略对超级电容和电池的充放电深度得到了效保护，波动较小的频率更有利于风储系统并网的电能质量，对电网调度也会更加友善，使得风储电站跟踪电网调度的可靠性更高。