海上风电机组DeepCWind平台系泊缆布置及断裂仿真分析

黄心伟, 柳亦兵, 刘剑韬, 滕伟

(华北电力大学电站能量传递转化与系统教育部重点实验室, 北京 102206)

随着“双碳政策”的实施,中国的能源结构逐渐向低碳化转型,发展风电等可再生能源成为大势所趋[1]。与陆上风电机组相比,海上风电机组因风资源更强、更稳定,单机容量更大,利用小时数更多以及邻近东部沿海负荷中心等优点逐渐成为未来风电的发展重心[2-3]。目前,海上风电机组主要以固定式为主,随着海上风电向深远海发展,漂浮式风电机组因具有更好的经济和技术优势开始受到海洋工程界的广泛关注,成为未来海上风电机组的主流发展方向。根据中国海洋风资源特点,半潜式平台因适用水深范围广、结构稳定性好和建造运输方便等优点成为当前阶段最为适合中国开发建设的漂浮式海上风电机组基础型式平台[4]。

漂浮式风电机组平台通过系泊系统固定在海床上,系泊系统是影响风电机组安全性的关键因素。中外学者对海上风电机组浮式平台的系泊系统进行了针对性研究。刘伟等[5]以5 MW单柱式浮式风电机组为研究对象,提出了一种考虑风浪流耦合的浮式风电机组运动响应和系泊缆疲劳分析方法,计算了系泊缆的疲劳寿命。吴国强等[6]以OC4-DeepCWind半潜式浮式平台为研究对象,探究了不同入流方向、系泊缆长度以及系泊缆断裂对浮式平台运动响应的影响。Bae等[7]研究了系泊缆突然断裂对浮式风电机组平台运动性能的变化,结果表明系泊缆断裂会导致明显的机舱偏航误差和平台漂移。Li等[8]研究了Spar型浮式平台在系泊缆断裂情况下的瞬态响应,结果表明就漂移距离而言,在某些情况下停机措施可能会使浮式风电机组的运动响应更危险。Yang等[9]研究了系泊缆破损对Barge浮式风电机组平台运动响应和剩余系泊缆张力的影响,并对额定工况和极端工况下系泊缆突然断裂的瞬态行为进行了分析和预测。

上述研究对系泊缆断裂情况下浮式平台的运动响应分析较多,而关于系泊缆的不同角度布置形式对浮式平台稳定性和安全性方面的研究较少。因此,现以美国国家可再生能源实验室(National Renewable Energy Laboratory, NREL)的NREL 5 MW风电机组和OC4-DeepCWind半潜式浮式平台为研究对象,基于ANSYS/AQWA水动力分析软件和OPENFAST仿真分析软件,研究不同系泊缆数量、角度布置形式以及系泊缆断裂等因素对浮式风电机组平台运动响应和系泊缆张力的影响。

1 漂浮式风电机组载荷分析

1.1 风电机组受力模型

漂浮式海上风电机组在海洋环境中主要受到海风、波浪及海流3种外部环境载荷的作用,如图1所示。

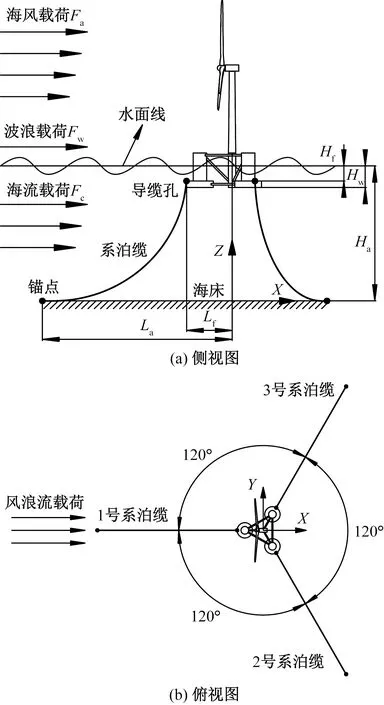
Lf为导缆孔与浮式平台中心的横向距离(导缆孔半径);Hf为导缆孔与水面线的垂直距离(导缆孔深度);La为锚点与浮式平台中心的横向距离(锚点半径);Ha为水深(锚点深度);Hw为浮式平台吃水深度图1 漂浮式海上风电机组载荷受力模型Fig.1 Load force model of floating offshore wind turbine

1.2 风载荷

工程中通常采用Kaimal风速谱[10]模拟湍流风。浮式风电机组所受的风载荷Fa[11]为

Fa=ChCsAaPa

(1)

式(1)中:Ch为高度系数,取值为1.0;Cs为形状系数,取值为0.5;Aa为风电机组受风力部分的等效面积,m2;Pa为风压,kPa。

(2)

式(2)中:ρa为空气密度,取值为1.225 kg/m3;Va为设计风速,m/s。

1.3 波浪载荷

海洋工程界普遍以波浪谱的形式从能量分布角度来模拟不规则波浪。现阶段常用的波浪谱为JONSWAP谱,该谱适用于未充分发展的海浪,由有义波高Hs、谱峰周期Tp和谱峰升高因子γ共同决定。OC4-DeepCWind浮式平台属于大尺度构件(D/λ>0.2),其中,D为构件截面的特征尺度;λ为入射波长。浮体对入射波浪的影响不可忽略,故采用势流理论计算波浪载荷。

在势流理论中,假设海水为无旋、无黏和不可压缩的理想流体,则浮体结构周围流场总速度势φ[12]为

φ(x,y,z,t)=φI+φD+φR

(3)

式(3)中:x、y、z分别为浮体结构在3个自由度方向上的位置坐标;t为时间变量;φI为入射波速度势;φD为绕射波速度势;φR为辐射波速度势。各速度势需要满足拉普拉斯方程和边界条件。

(4)

满足上述条件后,波浪载荷作用在结构物上的波浪力Fw和波浪力矩Mw为

(5)

式(5)中:s为浮体湿表面;r为浮体表面任一点至力矩作用点的径向矢量;Pw为水压,Pw通过线性化的伯努利方程以速度势表达为

(6)

式(6)中:ρw为海水密度,取值为1 025 kg/m3。

1.4 海流载荷

海洋中深水区域的海流流速随水深呈线性变化,属于剪切流。相较于风载荷和波浪载荷,海流质点的运动速度和周期随时间变化缓慢,作用在基础水面以下的海流载荷力Fc为

(7)

式(7)中:CD为拖曳力系数;Ac为浮式平台受流力部分的等效面积,m2;Vc为海流速度,m/s。

1.5 系泊缆受力分析

系泊系统采用悬链线式系泊缆,通过悬垂的钢制锚链与海底接触,由悬链线的几何作用和锚链自身重力产生回复力以实现浮式平台的定位。

图2为系泊缆动态模型示意图,系泊缆由N个均匀大小的莫里森单元组成,每段系泊缆的密度和尺寸特性都相同。

Sj为锚点与系泊缆第j个节点之间的未拉伸长度;De为系泊缆单元的直径图2 系泊缆动态模型示意图Fig.2 Dynamic model diagram of mooring cable

系泊缆任意单元的运动方程[13]为

(8)

式(8)中:T为系泊缆单元节点处的张力向量;V为剪力向量;R为位置向量;M为弯矩向量;Se为系泊缆单元的未拉伸长度;w为系泊缆单元每单位长度的重量;Fh为每单位长度的水动力载荷矢量;me为每单位长度的质量;q为每单位长度的分布力矩载荷。

系泊缆所受的弯矩M和张力T的表达式为

(9)

式(9)中:EI为系泊缆的弯曲刚度,kN/m;EA为轴向刚度,kN/m;ε为轴向应变。

2 风电机组模型设计

2.1 风电机组参数

漂浮式海上风电机组DeepCWind平台的结构参数主要分为风电机组、浮式平台和系泊系统三部分,其中上部风电机组结构选用NREL 5 MW风电机组,技术参数如表1所示[14]。基础结构选用OC4-DeepCwind半潜式浮式平台,技术参数如表2所示[15]。系泊系统由悬链线式锚链组成,具体参数如表3所示。

表1 NREL 5 MW风电机组参数Table 1 Parameters of NREL 5 MW wind turbine

表2 OC4-DeepCWind浮式平台参数Table 2 Parameters of OC4-DeepCWind floating platform

表3 悬链线系泊缆参数Table 3 Parameters of catenary mooring cable

2.2 有限元建模

图3为浮式风电机组平台模型及网格分布图。模型网格划分要求1个波长至少覆盖7个最大网格单元尺寸,故划分网格单元越小,计算分析精度越高,但同时分析时间也就越长[16]。该模型网格划分的最大单元尺寸设置为1.5 m,水平面以下绕射单元总数约为8 000,总单元数约为17 000。浮式风电机组平台的横支撑和斜支撑简化为莫里森单元,其余部分为面单元。

图3 漂浮式风电机组平台模型及网格分布Fig.3 Platform model and grid distribution of floating wind turbine

2.3 自振周期验证

不考虑外部环境载荷,设置浮式平台位移或摆动的初始位置相对于原位置分别为1 m或1°,得到其在6个自由度方向上的自由衰减曲线如图4所示。

图4 浮式平台自由衰减曲线Fig.4 Free attenuation curve of floating platform

表4为自振周期与Coulling等[17]得到的实验自振周期的比较。本文浮式平台在纵荡、横荡和艏摇方向的自振周期偏大,垂荡、横摇和纵摇方向偏小,但整体误差相对较小,验证了仿真分析的可靠性。

3 系泊系统仿真分析

3.1 工况设置

本文计算工况主要考虑浮式风电机组在正常运行时的工作海况和停机状况下的极端海况,如表5所示[18]。

表4 自振周期计算结果对比Table 4 Comparison of natural vibration period

表5 海洋环境参数Table 5 Parameters of ocean environment

3.2 系泊系统设计要求

为保证浮式风电机组平台在正常运行过程中的稳定性和安全性,系泊系统需要满足基本设计要求。

(1)系泊缆张力满足安全性能要求。按照中国船级社(China Classification Society, CCS)规范的系泊系统设计要求,系泊缆张力安全系数Sf[19]定义为

(10)

式(10)中:Smbs为系泊缆的破断强度,kN;Tmax为系泊缆承受最大张力,kN。

系泊缆张力安全系数如表6所示。

表6 系泊缆安全系数表Table 6 Safety factor table of mooring cable

(2)系泊缆的卧链长度不能小于零。

(3)浮式平台的运动极值符合要求。在水平位移方面,一般情况下最大水平位移不得超过水深的一半[20]。在俯仰运动方面,需满足平均俯仰角小于±5°,动态俯仰角小于±15°[21]。

3.3 工作海况下系泊系统数量布置分析

三根系泊缆数量布置形式由于缆绳数量少的缺点,若迎浪侧系泊缆发生疲劳或破坏断裂失效,极有可能导致浮式平台的大幅漂移或倒塌。本节将同一个浮筒上的系泊缆分为一组,分别设置六根系泊缆布置和九根系泊缆布置中的同组相邻系泊缆夹角为10°和5°,研究不同系泊缆数量对浮式平台稳定性和安全性的影响,具体布置形式如图5所示。

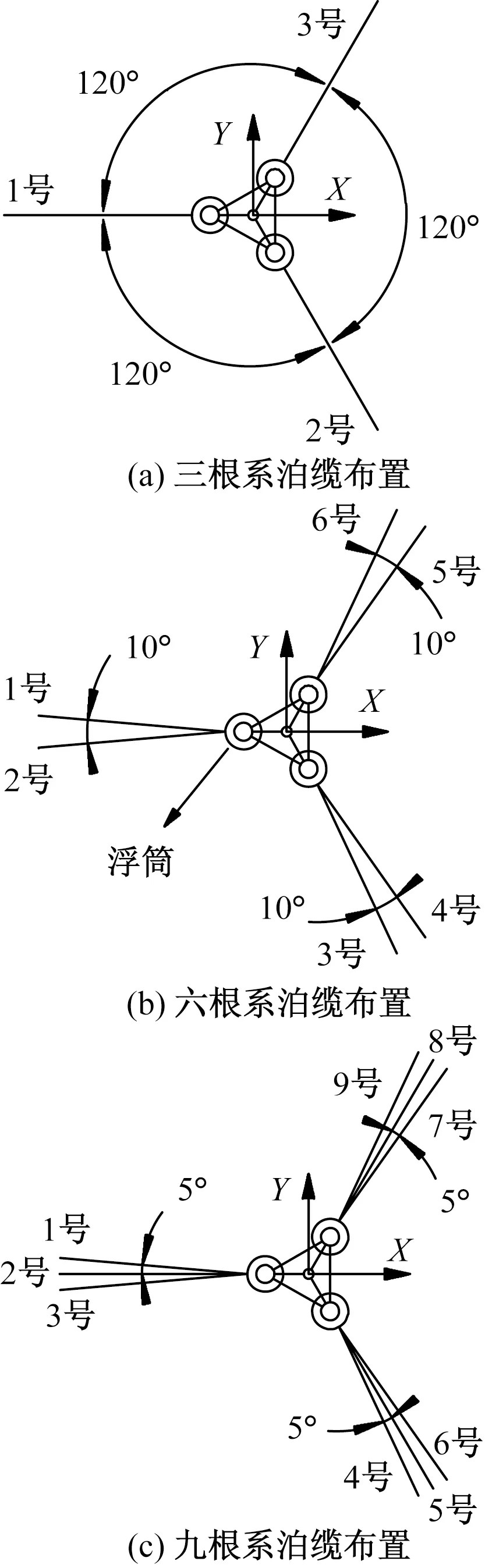
图5 不同系泊缆数量布置形式Fig.5 Arrangement forms of different cable numbers

设置沿x轴(0°)方向为风浪流载荷入射方向,仿真时长为3 600 s。为确保更清楚地显示浮式平台的时域运动响应变化,选取500～2 500 s时间段内的运动响应结果。图6为工作海况不同系泊缆数量下浮式平台纵荡、横荡和艏摇方向上的运动响应曲线。图7为浮式平台在6个自由度方向上的运动峰值和峰峰值统计结果。其中峰值为浮式平台稳定后距初始位置的运动最大值,峰峰值为浮式平台稳定后最大值和最小值的差值,表示浮式平台的最大波动情况。图8为不同系泊缆数量下浮式平台最大系泊缆张力和最小安全系数统计结果。

图6 不同系泊缆数量布置下浮式平台时域运动响应Fig.6 Time-domain motion response of floating platform under different number of mooring cables

图7 不同系泊缆数量布置下运动峰值和峰峰值结果Fig.7 Statistical results of motion peak and peak-to-peak value under different number of mooring cables

图8 不同系泊缆数量布置下最大系泊缆张力和最小安全系数结果Fig.8 Statistical results of maximum mooring cable tension and minimum safety factor under different number of mooring cables

由图6～图8可知,随着系泊缆数量的增多,浮式平台在除垂荡的5个自由度方向上的运动峰值和峰峰值均有减小。其中,六根系泊缆数量布置相较于三根系泊缆在纵荡、横荡和艏摇方向的运动峰值分别下降了36.75%、34.25%和30.21%,显著提高了浮式平台的稳定性。由图8可知,随着系泊缆数量的增多,最大系泊缆张力逐渐降低。其中,六根系泊缆数量布置相较于三根系泊缆,最大系泊缆张力降低了24.23%,显著提高了系泊系统的安全性。九根系泊缆布置虽能进一步降低浮式平台的运动响应和系泊缆张力,但相比于六根系泊缆,其对浮式平台的运动稳定性优化不明显,且九根系泊缆数量布置提高了系泊系统的制造和安装成本。根据实际应用中浮式平台的稳定性和安全性要求,选择六根系泊缆数量布置形式。

3.4 工作海况下系泊系统角度布置分析

在三根以上系泊缆数量布置形式中,系泊缆不同角度布置对浮式平台的运动响应和缆绳张力影响不可忽略。本节对六根系泊缆不同角度布置形式进行浮式平台的运动响应和系泊缆张力分析。设置沿浮式平台中心与浮筒中心连线转动的系泊缆角度区间为5°～45°,每相隔5°布置为一组,共分为9组,系泊缆具体角度布置形式如图9所示。

图9 系泊缆不同角度布置形式Fig.9 Layout form of mooring cable at different angles

图10为浮式平台在6个自由度方向上的运动峰值和峰峰值结果。图11为不同系泊缆角度布置形式中最大系泊缆张力和最小安全系数统计结果。

图10 不同系泊缆角度布置下运动峰值和峰峰值结果Fig.10 Statistical results of motion peak and peak-to-peak value under different mooring cable angles

图11 不同系泊缆角度布置下最大系泊缆张力和最小安全系数结果Fig.11 Statistical results of maximum mooring cable tension and minimum safety factor under different mooring cable angles

由图10可知,随着系泊缆布置角度的增大,浮式平台在纵荡、横荡和艏摇方向的运动峰值和峰峰值均有明显降低。在垂荡、横摇和纵摇方向,系泊缆布置角度的增大使浮式平台垂荡和纵摇方向的运动峰值升高,横摇运动峰值降低,但峰峰值变化不大。从图11可看出,随着布置角度的增大,系泊缆最大张力逐渐增大,最小安全系数逐渐减小。当布置角度超过40°时,系泊缆最小安全系数低于完整工作工况下的安全系数2.25,不能保证浮式平台的安全性能要求。由此可见,增大系泊缆布置角度可提高浮式平台的稳定性,但同时会使系泊缆张力增大,影响系泊系统的安全性。

3.5 极端海况下系泊缆断裂分析

漂浮式风电机组由于长期处于海洋环境载荷作用下,其系泊系统容易产生断裂失效。系泊缆失效方式主要有以下两种:①长期受到风、浪、流以及海底磨损等周期性载荷作用下的疲劳失效;②台风等极端环境载荷作用下的断裂失效。系泊缆失效会导致浮式平台的运动响应急剧变化,影响风电机组的正常运行。严重情况下剩余系泊缆的张力可能会超过材料强度极限,导致更严重的事故。故需对系泊系统进行极端环境载荷作用下的断裂分析研究,以保证浮式平台系统的稳定性和安全性。

本节研究了不同系泊缆角度布置下,迎浪侧系泊缆断裂对浮式风电机组平台时域运动响应和安全性能的影响。浮式风电机组在极端载荷环境下采用停机措施,关闭风力发电机,并设置叶片桨距角为顺桨(90°)。设置2号迎浪侧系泊缆在1 500 s时发生断裂,系泊缆布置方式如图12所示。

图12 不同系泊缆角度布置下2号系泊缆断裂情况图Fig.12 Fracture diagram of No.2 cable under different mooring cable angles

图13为5°系泊缆布置形式下,系泊缆完好和断裂后浮式平台在纵荡、横荡和艏摇自由度方向上的时域运动响应结果。由图13可知,由于2号系泊缆在1 500 s时突然断裂,浮式平台在1 500～1 800 s产生了很大的瞬态波动。相比于系泊缆完好情况,断裂状况下浮式平台在纵荡、横荡和艏摇方向的瞬态波动分别增大了约2.34倍、10.34倍和25.63倍,1 800 s后浮式平台逐渐趋于稳定。

图13 系泊缆断裂情况下浮式平台时域运动响应Fig.13 Time-domain motion response of floating platform under mooring cable fracture

图14和图15分别为不同系泊缆角度布置下,浮式平台在系泊缆完好、断裂(瞬态)和断裂(稳态)情况下的运动峰值和峰峰值统计结果。相比于系泊缆完好情况,2号系泊缆断裂后,浮式平台在纵荡、横荡、横摇、纵摇和艏摇方向的运动峰值和峰峰值明显增大,垂荡方向的运动响应减小。这主要是由于系泊缆断裂后系泊系统提供的回复刚度降低,导致浮式平台产生了较大的运动位移。由图14可以看出,断裂瞬态情况下,系泊缆布置角度的增大使浮式平台6个自由度方向的运动峰值均有明显增大。相比于断裂瞬态情况,浮式平台达到稳态后的运动峰值有所降低。

图14 系泊缆断裂情况下运动峰值比较Fig.14 Comparison of motion peaks under mooring cable fracture

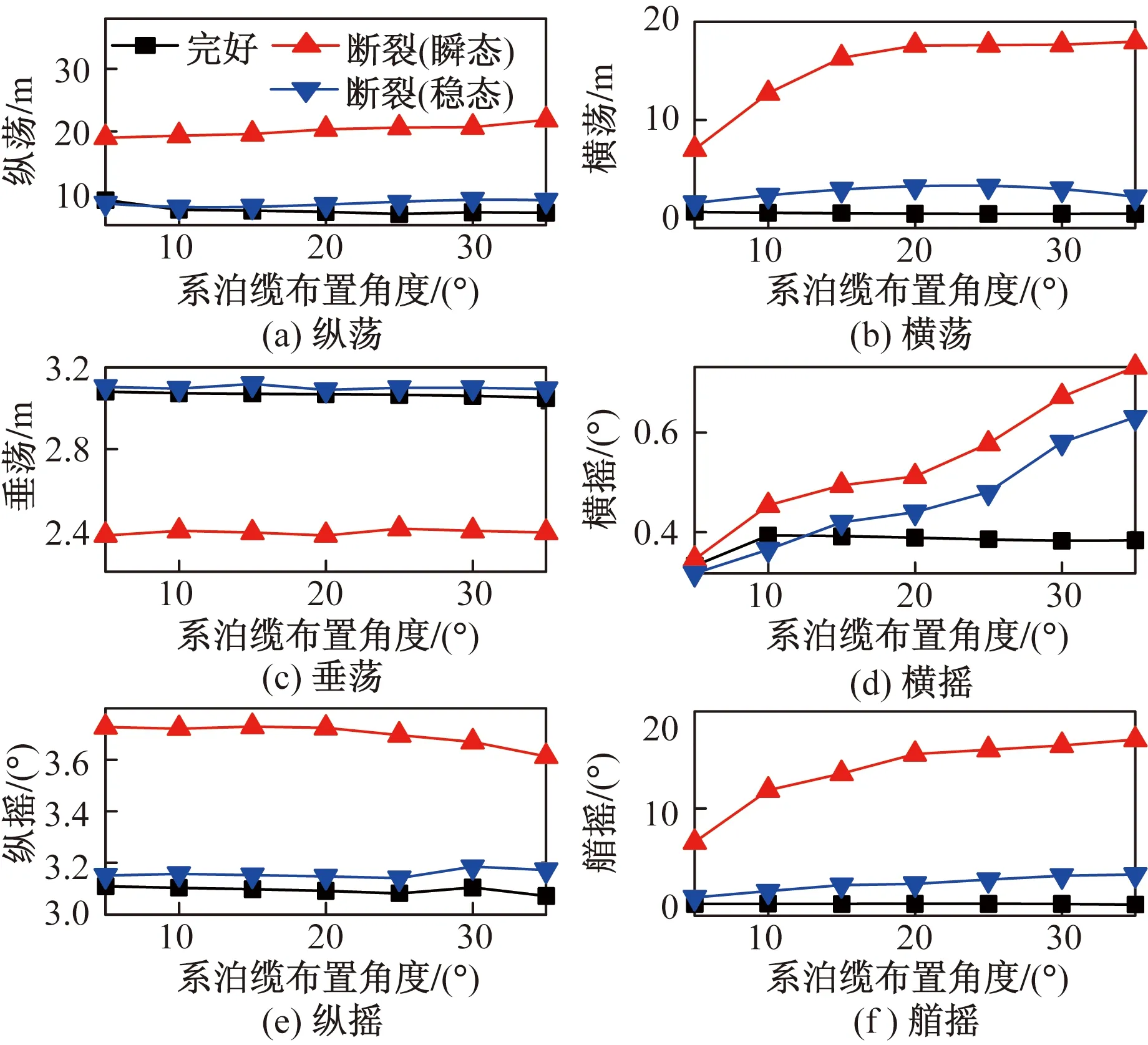
图15 系泊缆断裂情况下运动峰峰值比较Fig.15 Comparison of motion peak-to-peak values under mooring cable fracture

由图15可以看出,断裂瞬态情况下,系泊缆布置角度的增大使浮式平台纵荡、横荡、横摇和艏摇方向的运动峰峰值显著增大,纵摇方向的运动峰峰值降低,垂荡方向的运动峰峰值变化不明显。相较于系泊缆完好情况,断裂稳态情况下,浮式平台在纵荡、横荡、垂荡、纵摇和艏摇方向的运动峰峰值变化不明显,说明系泊缆断裂稳态后浮式平台的波动范围较为稳定。

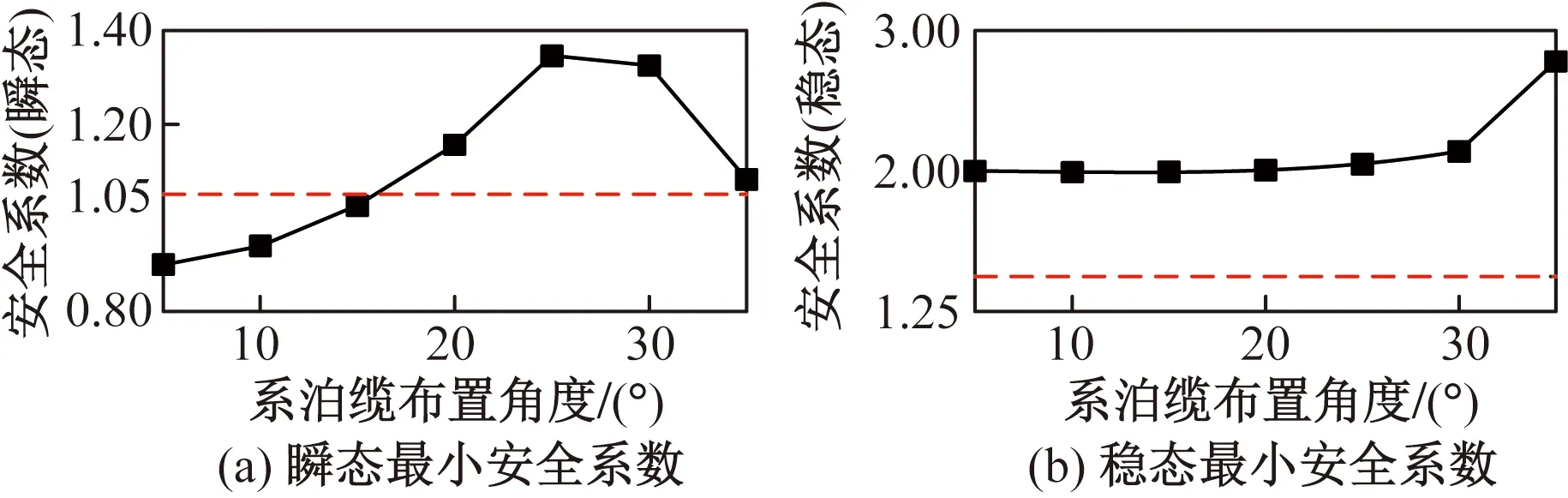
图16 系泊缆断裂情况下最小安全系数结果Fig.16 Statistical results of minimum safety factor for mooring cable fracture

图16为不同系泊缆角度布置形式中系泊缆在瞬态和稳态时的最小安全系数统计结果。由图16中的最小安全系数瞬态统计结果可以看出,5°～20°范围内的最小安全系数低于瞬态生存工况下的安全系数1.05,此时系泊系统不能保证浮式风电机组的安全性。由图12可知,由于2号系泊缆断裂后,系泊系统的受力平衡被打破,浮式平台向右上区域运动,1号和3号系泊缆承受张力增大。5°～25°范围内,1号系泊缆为主要受力缆绳,其安全系数为系泊系统最小安全系数。随着系泊缆布置角度的增大,1号系泊缆承受张力逐渐降低,最小安全系数增大,同时3号系泊缆承受张力逐渐增大。当系泊缆布置角度大于30°时,3号系泊缆的布置角度由背浪侧改为迎浪侧,承受张力大于1号系泊缆,为主要受力缆绳,故系泊系统的最小安全系数降低。相比于断裂瞬态情况,断裂稳态情况下系泊缆的最小安全系数始终满足破损生存工况下的安全性能要求。

4 结论

以NREL 5 MW风电机组和OC4-DeepCWind半潜式浮式风电平台为研究对象,通过有限元建模仿真分析,讨论不同系泊缆数量、角度布置形式以及系泊缆断裂等因素对浮式风电机组平台运动响应和系泊缆张力的影响,得到以下结论。

(1)增加系泊缆数量使浮式平台除垂荡的5个自由度方向上的运动峰值和峰峰值明显降低,提高了浮式平台的稳定性,但同时增加了系泊缆的制造和安装成本。工作海况下,相较于三根和九根系泊缆,六根系泊缆布置更符合浮式平台在实际应用中的稳定性和安全性要求。

(2)增大系泊缆布置角度使浮式平台纵荡、横荡和艏摇方向的运动峰值和峰峰值显著降低,但同时增大了迎浪侧系泊缆张力,导致最小安全系数减小。故在满足系泊系统安全性能的前提下,选择大角度的系泊缆布置形式,以提高浮式平台的稳定性。

(3)迎浪侧系泊缆断裂后,系泊系统提供的回复刚度降低,系泊缆布置角度的增大使浮式平台的运动峰值和峰峰值显著增大,降低了浮式风电机组平台的稳定性。系泊缆布置角度在5°～20°范围内,断裂瞬态情况下系泊系统的最小安全系数低于瞬态生存工况下的安全系数1.05,不能保证浮式风电机组的安全性。