平面镜中的角

沈冉

数学就在我们身边。平面镜是我们生活中熟悉的物品，其中也蕴含许多数学知识。下面就让我们一起走近平面镜，思考一道以“平面镜”为背景的数学问题。

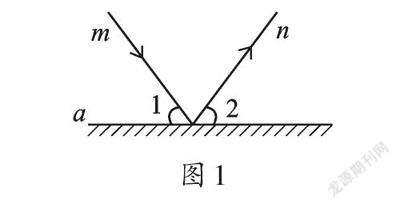
实验证明：平面镜反射光线的规律是照射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等。如图1，一束光线m射到平面鏡a上，被a反射后的光线为n，则入射光线m、反射光线n与平面镜a所夹的锐角相等，即∠1=∠2。

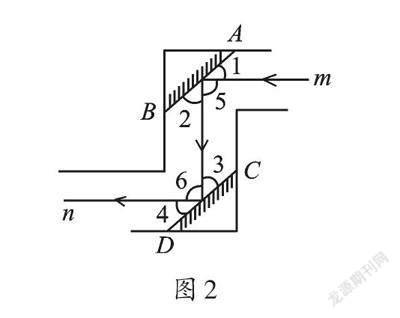
问题1：利用这个规律，人们制作了潜望镜。图2是潜望镜工作原理示意图，AB、CD是平行放置的两面平面镜。请解释进入潜望镜的光线m为什么和离开潜望镜的光线n是平行的。

【解析】图2中角比较多，我们要仔细观察角与角之间的位置关系。由于AB∥CD，根据“两直线平行，内错角相等”，可知∠2=∠3。根据平面镜的反射规律，可知∠1=∠2，∠3=∠4，∴∠1=∠2=∠3=∠4。而∠5=180°-∠1-∠2，∠6=180°-∠3-∠4，∴∠5=∠6。∴m∥n。理由是：内错角相等，两直线平行。

问题2：如图3，改变两个平面镜之间的位置关系，经过两次反射后，入射光线m与反射光线n之间的位置关系会随之改变。若入射光线m与反射光线n平行，但方向相反，则两个平面镜的夹角∠ABC为多少度？

【解析】∠ABC是△ABC的内角，根据三角形内角和定理，可知∠ABC=180°-（∠2+∠3）。因此，只需求出∠2+∠3的度数即可。

∵m∥n，

∴∠DAC+∠ACE=180°。

又∵∠1+∠2+∠DAC=180°，

∠3+∠4+∠ACE=180°，

且∠1=∠2，∠3=∠4，

∴2∠2+2∠3=180°，

即∠2+∠3=90°。

∴∠ABC=180°-90°=90°。

问题3：如图4，若90°＜α＜180°，入射光线EF与反射光线GH的夹角∠FMH=β，请探索α与β的数量关系，并说明理由。

【解析】观察图4可以发现：∠FMH是△MEG的内角，∠ABC是△BEG的内角，这两个三角形中的角都与∠2+∠3有联系。根据“三角形内角和为180°”，可得∠2+∠3=180°-α。

又∵∠1=∠2，∠3=∠4（反射原理），

∠1=∠MEB，∠4=∠MGB（对顶角相等），

∴∠MEG+∠MGE=2∠2+2∠3=2（∠2+∠3）=2（180°-α）=360°-2α。

在△MEG中，β=180°-（∠MEG+∠MGE）=180°-（360°-2α）=2α-180°，

即β=2α-180°。

问题4：如图5，若90°＜α＜180°，设镜子CD与BC的夹角∠BCD=γ（90°＜γ＜180°），入射光线EF与镜面AB的夹角∠1=m（0°＜m＜90°），已知入射光线EF从镜面AB反射到镜面BC，再反射到镜面CD，最后经镜面CD反射。当反射光线与入射光线EF平行时，探索m与γ的数量关系，并说明理由。

【解析】根据题意，画出大致图形，如图6所示，延长NM和FE，交点为G。

由问题3的思路可得∠G=180°-2m-2∠3=180°-2（m+∠4），∠MNH=180°-2∠5。

∵EF∥NH，

∴∠G+∠MNH=180°，

即180°-2（m+∠4）+180°-2∠5=180°。

整理，得m+∠4+∠5=90°。

∴m+（180°-γ）=90°，即γ-m=90°。

本题还可以有其他思路，感兴趣的同学可自行探究哦。