方程与不等式中考题型探究

朱赛兰

“方程与不等式”的中考题中既有对基础知识和技能的考查，又有对综合应用能力的考查。现归纳几例供同学们研究。

一、新定义型运算

例1 （2022·浙江宁波）定义一种新运算：对于任意的非零实数a、b，a⊗b=[1a][+1b]。若（x+1）⊗x=[2x+1x]，则x的值为 。

【解析】根据新定义列出分式方程[1x+1][+1x]=[2x+1x]，解方程即可得出x=[-12]。

【小结】此题定义的是一种新运算，定位于我们熟悉的分式。我们需要理清算法，呈现公式，将问题从公式到分式方程，逐步转化，从数学情境中建立模型，实现对理解能力和转化能力的考查。

二、含参数的方程（组）

例2 （2022·山东聊城）关于x、y的方程组[2x-y=2k-3，x-2y=k]的解中，x与y的和不小于5，则k的取值范围为（ ）。

A.k≥8 B.k＞8 C.k≤8 D.k＜8

【解析】关于含参数类型的求解问题，先不要着急消元求解，要观察系数，思考x与y的和能否通过整体加减用参数表示出来，再列不等式求解。将方程组中的两式相减，得x+y=k-3。由已知，得x+y≥5，则k-3≥5，解得k≥8。故选A。

【小结】本题是方程与不等式的结合，考查了等式性质与不等式的解法，解题的关键是应用整体思想将含参式与已知条件建立联系。

三、方程与函数结合

例3 （2022·浙江绍兴）已知抛物线y=x2+mx的对称轴为直线x=2，则关于x的方程x2+mx=5的根是（ ）。

A.0，4 B.1，5 C.1，-5 D.-1，5

【解析】根据抛物线y=x2+mx的对称轴为直线x=2，则[-m2×1]=2，解得m=-4。然后解一元二次方程x2-4x=5即可。故选D。

【小结】本题通过二次函数的对称轴公式建立一次方程模型，求出参数m的取值，最后解关于x的一元二次方程即可。本题知识点较多，综合考查了同学们的基础技能。

四、建立方程模型

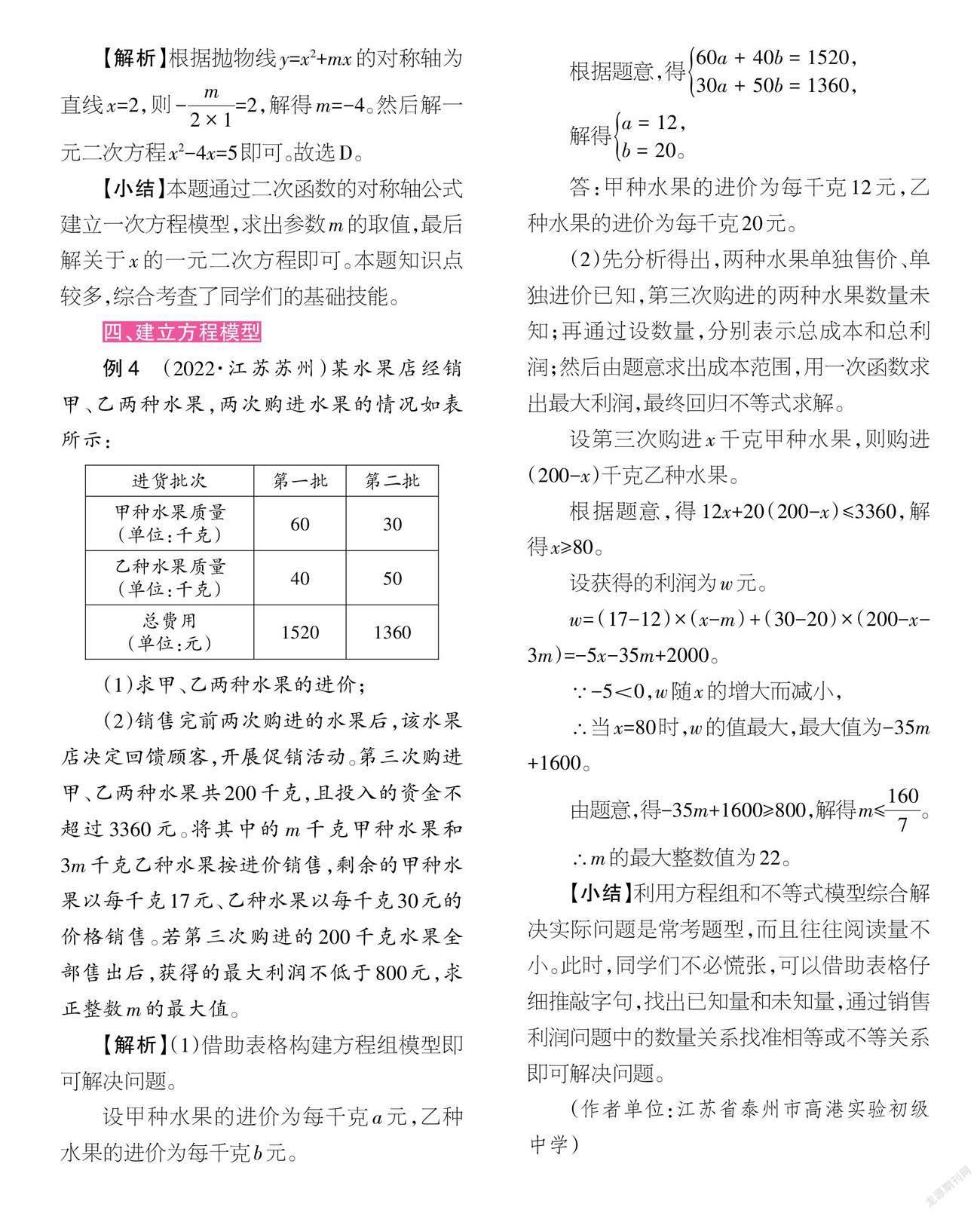
例4 （2022·江苏苏州）某水果店经销甲、乙两种水果，两次购进水果的情况如表所示：

（1）求甲、乙两种水果的进价；

（2）销售完前两次购进的水果后，该水果店决定回馈顾客，开展促销活动。第三次购进甲、乙两种水果共200千克，且投入的资金不超过3360元。将其中的m千克甲种水果和3m千克乙种水果按进价销售，剩余的甲种水果以每千克17元、乙种水果以每千克30元的价格销售。若第三次购进的200千克水果全部售出后，获得的最大利润不低于800元，求正整数m的最大值。

【解析】（1）借助表格构建方程组模型即可解决问题。

设甲种水果的进价为每千克a元，乙种水果的进价为每千克b元。

根据题意，得[60a+40b=1520，30a+50b=1360，]

解得[a=12，b=20。]

答：甲种水果的进价为每千克12元，乙种水果的进价为每千克20元。

（2）先分析得出，两种水果单独售价、单独进价已知，第三次购进的两种水果数量未知；再通过设数量，分别表示总成本和总利润；然后由题意求出成本范围，用一次函数求出最大利润，最终回归不等式求解。

设第三次购进x千克甲种水果，则购进（200-x）千克乙种水果。

根据题意，得12x+20（200-x）≤3360，解得x≥80。

设获得的利润为w元。

w=（17-12）×（x-m）+（30-20）×（200-x-3m）=-5x-35m+2000。

∵-5＜0，w隨x的增大而减小，

∴当x=80时，w的值最大，最大值为-35m

+1600。

由题意，得-35m+1600≥800，解得m≤[1607]。

∴m的最大整数值为22。

【小结】利用方程组和不等式模型综合解决实际问题是常考题型，而且往往阅读量不小。此时，同学们不必慌张，可以借助表格仔细推敲字句，找出已知量和未知量，通过销售利润问题中的数量关系找准相等或不等关系即可解决问题。

（作者单位：江苏省泰州市高港实验初级中学）