HTPB固体推进剂蠕变损伤模型研究

吴 轩，郑 健，许进升，李 辉，罗熙斌

(1.南京理工大学 机械工程学院，江苏 南京 210094；2.中国华阴兵器试验中心，陕西 华阴 714200)

引 言

作为固体火箭发动机的关键部件之一，固体推进剂药柱的结构完整性对发动机的性能发挥至关重要[1]。固体火箭发动机的整个寿命周期贮存过程中由于长期受重力影响产生蠕变现象，使药柱下沉产生变形，严重会改变药柱的燃面和安全性能[2-3]。为了保证装药的结构完整性，有必要对复合固体推进剂的蠕变性能进行研究。

固体推进剂的力学性能呈现典型的黏弹性特征，国内外研究人员将黏弹性力学应用于推进剂的研究，提出了表征其变形特性的本构模型。经典的微分型模型是利用弹簧和黏壶进行串并联组合形成不同的结构，建立具有微分形式的本构方程，主要包括Maxwell模型、Kelvin模型、三参量固体模型、Burgers模型等[4]。胡义文等[5]采用Burgers 模型描述PBT复合固体推进剂的高温蠕变，证实推进剂蠕变与应力以及温度相关。Zhang等[6]研究对比了三参量、Burgers、广义Kelvin、五参量、指数型蠕变模型这五种模型对双基固体推进剂蠕变特性的适应性。Bihari等[7]采用Kelvin-Voigt模型来表征固体火箭推进剂的粘弹性。王鑫等[8]分别采用位移传感器、计时器和试验机3种方案进行蠕变实验，并采用Norton模型对推进剂蠕变曲线进行拟合。然而在恒定应力下，一个完整的蠕变过程可分为3个阶段:衰减蠕变阶段、稳定蠕变阶段以及加速蠕变阶段[9]。上述微分型蠕变模型只能部分反应推进剂材料的蠕变特性，不能全面地描述推进剂蠕变过程，尤其是推进剂的加速蠕变阶段。

由于固体推进剂的制备工艺和环境因素会导致其颗粒与基体界面的浸润能力下降，导致材料内部存在随机分布的初始缺陷[10]，且极大程度地影响材料力学性能，当损伤累积到一定程度时，推进剂蠕变将达到蠕变破坏阶段。为了描述推进剂蠕变加速阶段的变形特性，研究人员引入损伤对经典黏弹性模型进行修正。Ho等[11]对复合推进剂的蠕变损伤进行了研究，使用最大应力的失效标准的线性累积损伤模型中得出损伤分数；Kunz R[12]结合连续损伤力学理论来建立推进剂损伤模型来描述推进剂力学性能；沈怀荣[13]针对复合固体推进剂材料建立了与温度相耦合的蠕变损伤演变模型，用以预估复合推进剂的寿命。但均未对推进剂蠕变本构方程以及蠕变机制等作具体分析。

本研究在Burgers模型的基础上结合连续损伤力学原理建立了一种改进的蠕变损伤模型，用于描述不同应力下HTPB复合固体推进剂的蠕变全过程，为开展立式贮存下固体推进剂药柱结构完整性分析提供理论基础。

1 蠕变损伤模型理论

1.1 蠕变本构模型

Burgers模型由一个Maxwell模型和一个Kelvin模型串联而成[6]，兼顾瞬时弹性和流体流动特征，其力学模型如图1所示。为研究材料的蠕变，设施加的应力载荷为σ(t)=σ0H(t)，其中H(t)为Heaviside函数，σ0为恒定应力。该模型的蠕变本构方程为：

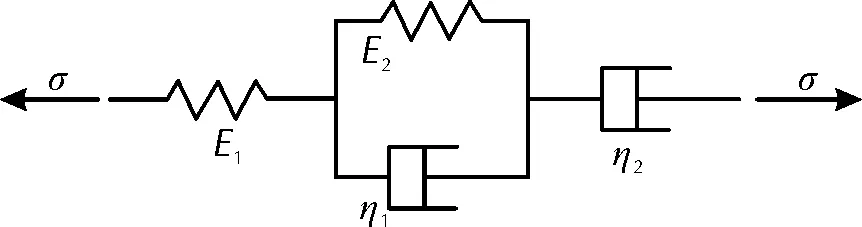
图1 Burgers模型Fig.1 Burgers model

(1)

式(1)左右同时对时间t求导得：

(2)

其中σ0/η1、σ0/η2、E2/η2均为恒定正值，随着时间t持续增加，应变曲线趋向于斜率为σ0/η1的直线。

Burgers模型应变与时间的关系如图2所示，可以描述固体推进剂的衰减蠕变和等速蠕变阶段。然而根据文献[9]，在较高蠕变应力下，应变率随着时间迅速增加并进入加速蠕变阶段直至破坏，需要结合损伤理论对该模型进行改进。

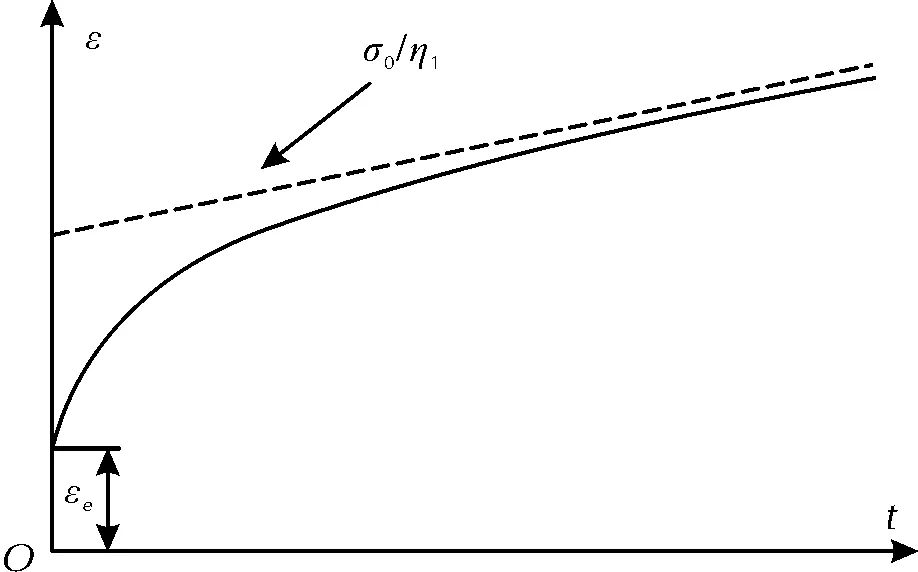
图2 Burgers模型蠕变示意图Fig.2 Burgers model creep diagram

1.2 蠕变损伤模型建立

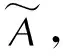
(3)

其中损伤因子D为无量纲的标量场变量，连续损伤模型必须要考虑损伤的演化，其演化规律可表示成损伤变量D和应力σ的函数。Stigh[15]通过对推进剂蠕变损伤实验研究，给出如下一种损伤演化方程：

(4)

式中：β为基于温度的材料参数；N为Laheru[16]定义的线性累积损伤模型的Lebesgue正应力，定义如下：

(5)

式中：σ0为在参考时间t0导致材料失效所需的蠕变应力；tf为蠕变破坏时间。

根据1.1节分析，由于Burgers模型中参数η1为常数，导致不能描述推进剂蠕变的加速过程，本研究将改进其黏壶用损伤变量D(0≤D≤1)来描述黏壶元件的劣化。根据Lemaitre[17]应变等效假设，黏壶在t时刻的蠕变损伤应变ε1(t)可以表示为：

(6)

式中：η*为含损伤的黏壶系数。

由式(6)可知，加入损伤使黏壶应变成为与材料损伤相关的函数，随着损伤的累积，黏性系数η*不断劣化，蠕变位移不断增大直至试件断裂。基于以上理论本研究提出一种蠕变损伤模型见图3。

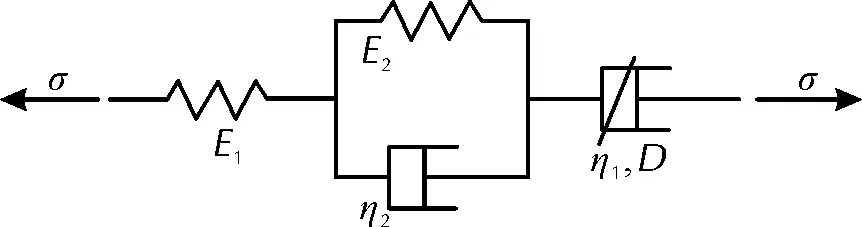
图3 蠕变损伤模型Fig.3 Creep damage model

本研究的蠕变损伤模型可以表示为：

(7)

1.3 蠕变机制讨论

复合推进剂在蠕变过程中同时存在蠕变硬化机制和蠕变损伤机制[4]。根据蠕变试验结果可以发现：当蠕变硬化机制占主导时，蠕变呈衰减状态；当蠕变损伤机制占主导地位时，蠕变呈现加速状态；而当两种机制接近时，则呈现为稳定蠕变阶段。为了验证上述蠕变机制的合理性，对蠕变损伤模型进行求导得到蠕变应变率：

(8)

再对时间进行求导得到蠕变加速度：

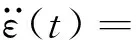
(9)

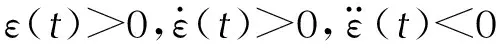
这表明在拐点之前，蠕变速度逐渐减小，此时蠕变硬化机制占据主导；在拐点之后，蠕变速度逐渐增大，表现为蠕变损伤阶段。这与试验描述的全过程蠕变曲线能较好地吻合，证明本研究所提出的蠕变损伤模型能很好地反应推进剂蠕变的特性。

2 试 验

2.1 试件制作与试验方法

试验对象是固体火箭发动机用HTPB复合推进剂药柱，由于复合推进剂弹性模量较小[18]，实验前发现推进剂较软，直接固定在实验设备的夹具上会发生脱落。从标准试样中切取推进剂试件，采用自行设计的与夹具适配的金属夹头(由45#钢制成)，夹头和推进剂试件由AB胶粘接固定，如图4所示。

图4 HTPB推进剂试件尺寸及装夹方式Fig.4 Size and clamping method of HTPB propellant test specimen

由于固体火箭发动机贮存温度一般为常温，本研究实验温度设定为25℃，在测试前将试样放在保温箱内保温24h以消除推进剂内部的残余应力。在进行蠕变试验前对推进剂材料进行了不同速率下单轴拉伸破坏试验，来确定蠕变试验的载荷水平。根据国军标GJB 770B-2005 413.2，进行加载速率分别为2、20、100mm/min的单轴拉伸试验，记录相应的复合推进剂应力—应变曲线，得到不同加载速率下推进剂的强度极限。

2.2 试验结果与分析

图5为不同速率下推进剂单轴拉伸应力—应变曲线，可知在单轴拉伸试验中，加载速率不同，材料的强度极限也不同，本研究选取加载速度为100mm/min下的应力峰值0.475MPa为推进剂材料的应力强度极限σs，为研究应力载荷对推进剂蠕变的影响，蠕变试验中应力取0.15、0.25、0.30、0.35MPa。图6为不同应力水平下HTPB复合推进剂的平均蠕变曲线。

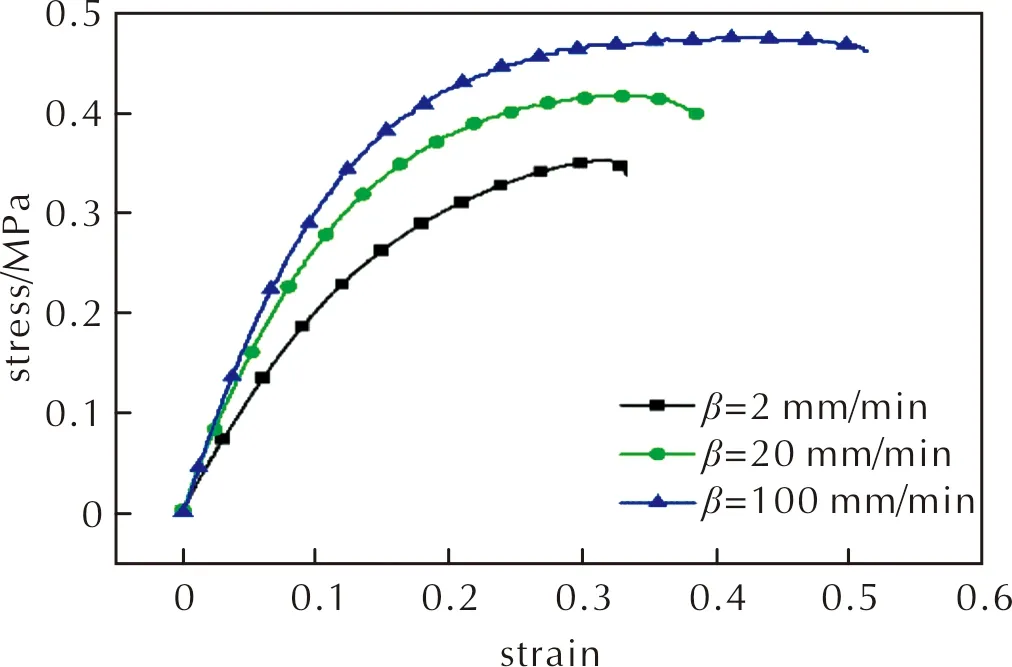
图5 不同速率下推进剂单轴拉伸应力—应变曲线Fig.5 Uniaxial tensile stress—strain curves of propellant at different rates

图6 不同应力水平下推进剂单轴拉伸蠕变曲线Fig.6 Uniaxial tensile creep curves of propellant under different stress levels

从图6可以看出，推进剂在0.3～0.35MPa载荷下的蠕变过程包括3个阶段，即衰减蠕变阶段、稳定蠕变阶段和加速蠕变阶段；在相同加载时间下，0.15～0.25MPa载荷作用下的蠕变过程则只有衰减蠕变阶段和稳定蠕变阶段。在衰减蠕变阶段，随着时间的增加，应变率逐渐减小，可称其为蠕变硬化[4]。与一般意义上的应变硬化不同，推进剂的蠕变硬化可以发生在较低的应力水平下，呈现出衰减蠕变。而在加速蠕变阶段，由于损伤的存在与演化，大大削弱了推进剂的力学性能，蠕变应变呈现明显的非线性增长，最终推进剂试件发生蠕变破坏。

3 模型参数获取与验证

3.1 模型参数获取与分析

根据文献[13]，材料参数β在常温下为定值，根据不同应力蠕变试验结果代入式(5)联立计算得出β≈4.784。为验证蠕变损伤模型的适用性，采用Levenberg-Marquardt优化算法来拟合不同应力水平下的蠕变试验数据，各拟合参数如表1所示，模型与试验结果吻合较好，拟合判定系数R2≥0.983。

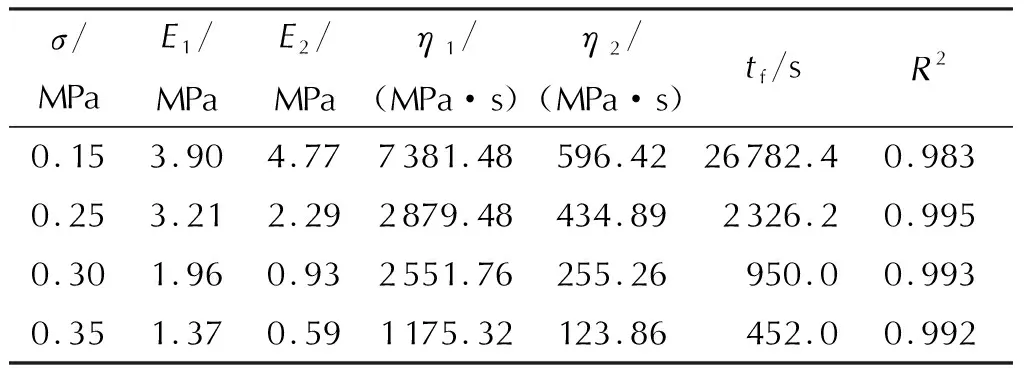
表1 不同应力水平下蠕变损伤模型参数Table 1 The creep damage model parameters under different stress levels

图7给出蠕变损伤模型与试验的拟合结果，该模型能有效描述HTPB复合固体推进剂在不同应力水平下的蠕变3个阶段。

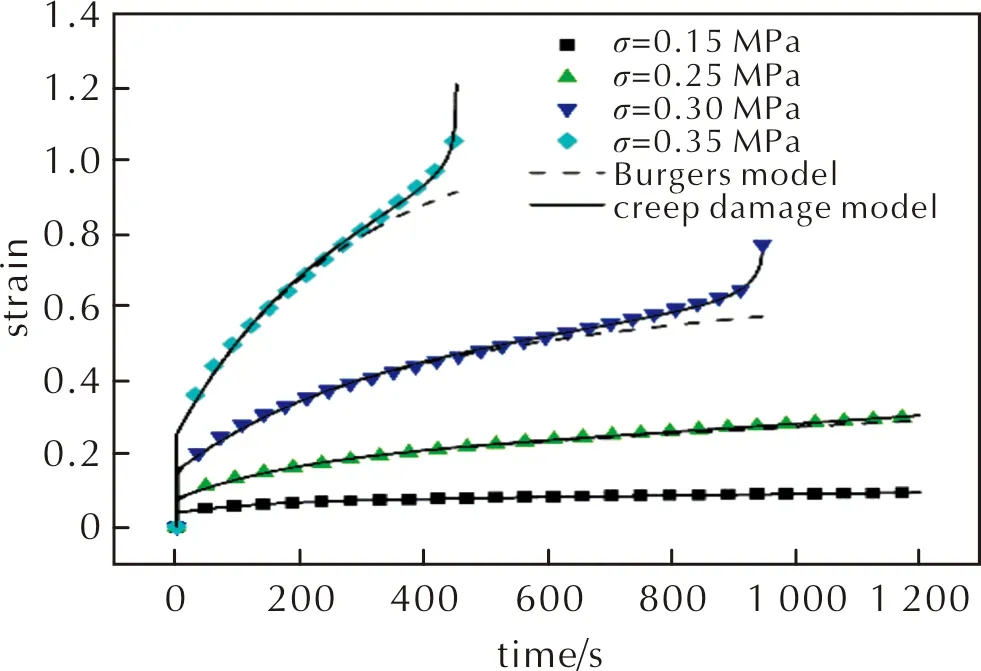
图7 蠕变试验曲线与理论曲线Fig.7 The test and theoretical curves of creep

图8为不同应力下推进剂的损伤演化曲线。由图8可以看出，HTPB复合固体推进剂在各个应力水平下，损伤在蠕变衰减阶段和稳定阶段随着时间缓慢增加，此时蠕变硬化机制占据主导；而在较大的应力下，当蠕变进入加速阶段，蠕变损伤劣化机制占据主导，表现为损伤随时间大幅增加导致蠕变破坏；在较小的应力下损伤增加极为缓慢近似呈线性增加。

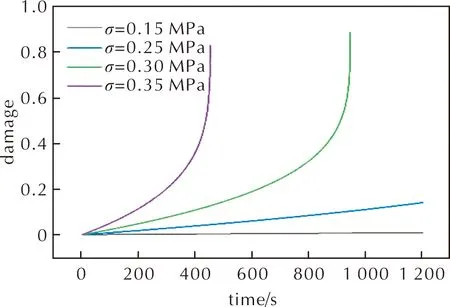
图8 损伤演化曲线Fig.8 Damage evolution curves

在工程应用中，研究人员常常关注材料的极限参数，为了分析两种模型对于推进剂材料蠕变应变的预测情况，采用式(10)获取模型在不同应力水平下的最大蠕变应变的误差：

(10)

由图7可以看出，Burgers模型和蠕变损伤模型与实验曲线相比，蠕变损伤模型与试验曲线的吻合度更高。图9为模型和试验曲线的误差值，在较低的应力下，两种模型的误差值都在5%以内；而在较高的应力下由于推进剂蠕变进入加速阶段，Burgers模型误差达到了20%以上，不能描述推进剂蠕变损伤阶段，而本研究的蠕变损伤模型在不同应力下的误差值均在3%以内，均能与试验数据很好地吻合。

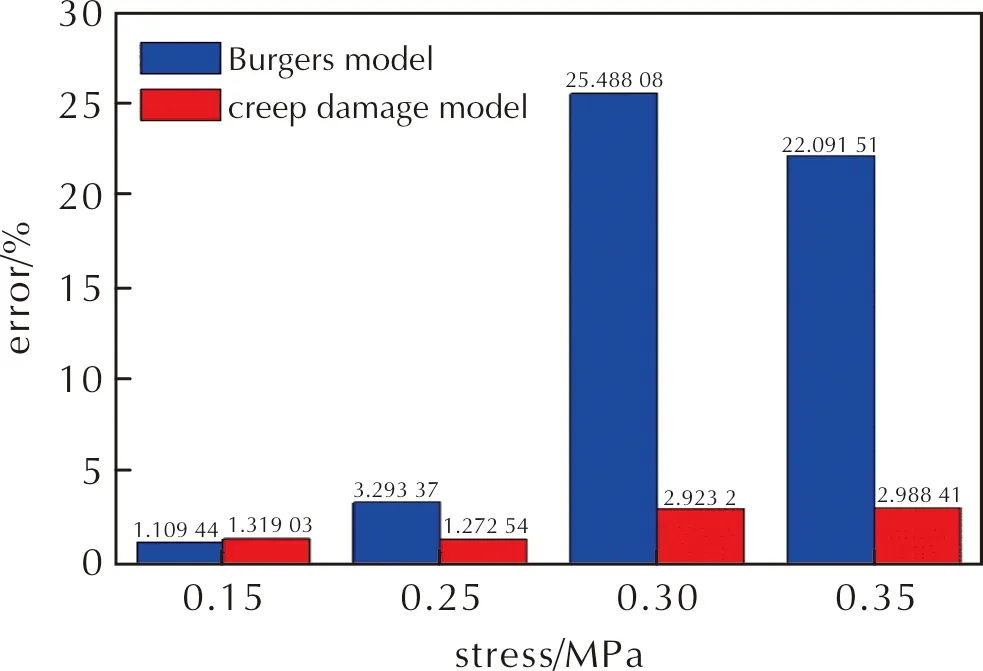
图9 不同应力下蠕变模型与实验数据的误差Fig.9 Errors between creep models and experimental data under different stresses

3.2 模型验证

由拟合数据看出不同应力下蠕变损伤模型的参数E1、E2、η1、η2、tf随着应力的增加而变化。Bihari B[7]假设Kelvin模型的弹簧和黏壶元件的参数随应力呈线性变化。由于本研究改进了黏壶，随着时间和应力的增加，该假设的误差也越来越大。根据表1中的数据，对η1采用指数函数形式，其他参数仍然沿用上述线性假设，拟合结果如图10所示。

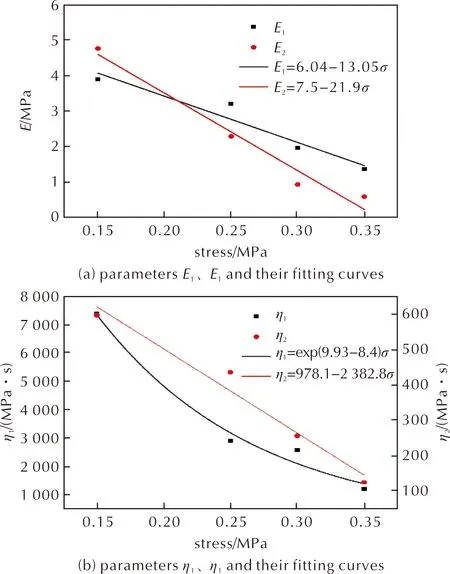
图10 模型参数及其拟合曲线Fig.10 Model parameters and their fitting curves

由此可以得出统一的蠕变损伤本构方程为：

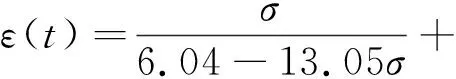
(11)

为了验证蠕变损伤模型在不同应力下复合推进剂蠕变的适用性，保持其他实验条件不变，进行0.2MPa下蠕变试验，根据式(13)计算出该应力下的模型参数如表2所示。图11为该蠕变应力下的试验结果和模型预测的对比结果，相关系数达到0.977，可以发现实验数据与模型预测结果吻合较好，表明本研究所建立的蠕变损伤模型可以很好地描述推进剂在不同应力下的蠕变力学行为。

表2 0.2MPa应力下模型预测参数Table 2 Model prediction parameters under 0.2MPa stress

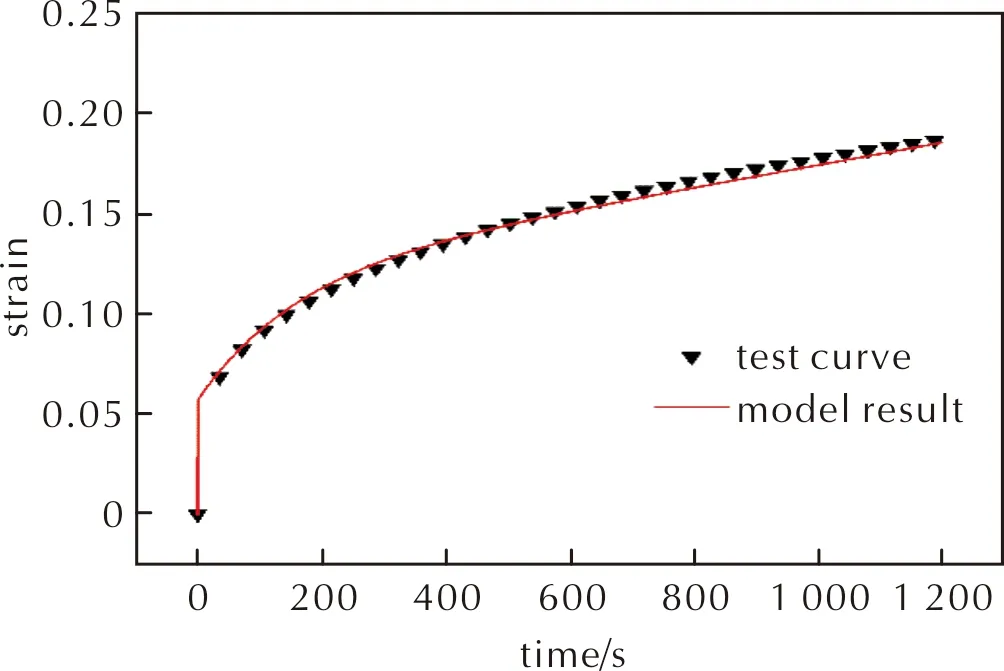
图11 蠕变试验结果和模型预测对比Fig.11 Comparison of creep test results and model predictions

4 结 论

(1)HTPB推进剂的蠕变过程可分为3个阶段：衰减蠕变、稳定蠕变和加速蠕变。在较高蠕变应力下，推进剂蠕变过程呈现典型的蠕变三阶段；在较低蠕变应力下，短时间内推进剂不会出现加速蠕变阶段。

(2)推进剂在衰减蠕变阶段内部基本不存在损伤，损伤曲线较为平滑；而进入稳定蠕变阶段后，随着蠕变时间的增加，损伤不断积累，且所施加的应力水平越高，损伤增长越快；当蠕变进入破坏阶段，损伤值迅速增长直至材料破坏。

(3)结合Burgers模型的特征和连续损伤力学理论，串联含损伤的黏壶元件，克服了Burgers模型无法反映蠕变破坏阶段特性的不足。本研究提出的蠕变损伤模型与试验值拟合度高，误差在3%以内。该模型可为准确开展立式贮存固体推进剂药柱在重力载荷下的结构完整性分析提供理论基础。