天基物联多码率QC-LDPC码构造方法研究

刘哲铭，成俊峰，魏 肖，缪德山，张 景，陆 洲

(1.中国电子科技集团公司 电子科学研究院，北京 100041;2.电信科学技术研究院有限公司 无线移动通信国家重点实验室，北京 100083)

0 引言

随着物联网技术的快速发展，其在各个领域的应用也急速拓展，为人们生活带来了极大的便利。然而，目前由于在大范围、恶劣环境条件下基站的建设成本高且难以维护，物联网仅仅在城市和部分乡村地区以及偏远地区的局部区域得以应用，其有限的覆盖范围致使物联网技术的服务能力受到限制。面对更加广阔的海洋、林地、山地等资源监测、数据采集，以及空域飞行器的指控信息传输等需求没有得到有效满足。卫星通信的快速发展则为信号的广域覆盖提供了很好的解决思路，3GPP标准小组已提议将卫星通信与地面通信纳入5G网络，星地通信技术的融合作为未来通信的发展趋势，以卫星为基础的天基物联网具有覆盖范围广、系统容量大、抗毁能力强以及不受恶劣天气的影响等优势[1-4]。

天基物联网业务主要包括数据采集、指挥控制以及数据广播等，重点聚焦在小数据传输[5]。卫星通信因其具有的优势受到广泛的关注，但在应用中面临着很多技术挑战，例如：星地信息传输距离长、信道变化速度快，数据传输易受雨雪天气影响等导致信息传输可靠性降低，因此，需要采用差错控制技术以提高信息传输准确性与可靠性。由于星地信息传输距离长，自动重传请求(ARQ，automatic repeat request)方案并不符合实际需求，混合自动重传请求(HARQ，hybrid automatic repeat request)方案显著提高了数据传输的有效性和传输速率[6]，前向纠错(FEC，forward error correction)方案则是其中的重点部分。为了给星地通信提供高可靠的数据传输过程，必须使用性能较优的信道编码，误比特率能达到10-7，例如：Turbo码[7]、低密度奇偶校验(LDPC，low-density parity-check)码[8]、Polar码[9]等以实现较低的误码率。其中，LDPC码具有较强的纠错能力，可以大大提高系统数据传输的可靠性，降低数据传输的错误率，且在很多领域都得到成熟的运用，本文重点以LDPC码为核心对天基物联场景下的信道编码进行研究。

在传统的卫星通信系统中，为了保证系统的可靠性和可用性，通常采用固定的传输方法进行传输，这种传输方式并不能根据信道条件的变化以及资源的利用率等信息进行灵活的调整。因此，为了充分利用信道资源，基于链路特性自适应数据传输技术得以快速发展，参考文献[10]中提到基于准循环LDPC(QC-LDPC， quasi-cyclic LDPC，)编码的卫星自适应数据传输系统中，根据编码要求，对其编码和构建算法进行全面的分析优化，该方案已成功应用于嫦娥四号卫星中继项目中。参考文献[11]则是根据实际的信道状态来自适应的调整码率，该技术不仅有助于提高传输速率，而且有效地提高了频谱效率，作者首先获取具有高码率的校验矩阵，然后通过缩短技术，根据码率变化删除固定列以达到降低码率的效果，可以根据当前的信道状态自由地改变码率，更好的利用信道资源。针对LDPC码，大数据长码传输的性能已经得到很好的研究，天基物联主要为小数据短码传输，短码相较于长码有较低的延迟，对于卫星通信远距离传输来说也具有一定的优势。参考文献[12]中作者针对LDPC短码进行研究，通过有限几何性质，利用欧几里得几何和循环分解方法，并利用分解矩阵、排列矩阵和分布矩阵三个子矩阵来构造混合准循环LDPC(HQC-LDPC，hybrid quasi-cyclic LDPC)校验矩阵，该方案在短码信息传输的误码率性能上表现优异。

本文以天基物联为背景，针对小数据传输进行研究，并根据在固定码长条件下信息传输更能满足卫星通信系统的要求，受DVB-S2X标准中信道编码在固定码长条件下实现多码率的效果，以及5G LDPC信道编码校验矩阵类Raptor结构设计所表现得优异性能的启发，对校验矩阵进行设计，在保证编码性能的条件下实现固定码长条件下的多码率QC-LDPC (MR-QC-LDPC，multi-rate QC-LDPC)码的设计。本文第二节介绍以代数法设计循环系数表为基础，通过叠加构造方法设计QC-LDPC码的校验矩阵；第三节通过缩短与扩展操作在保持类Raptor结构不变情况下实现固定码长条件下的MR-QC-LDPC码的设计；第三节针对所设计的LDPC码进行不同码率条件下的性能对比仿真图；第五节对本文内容进行总结。

1 基于代数法的QC-LDPC码叠加构造设计方法

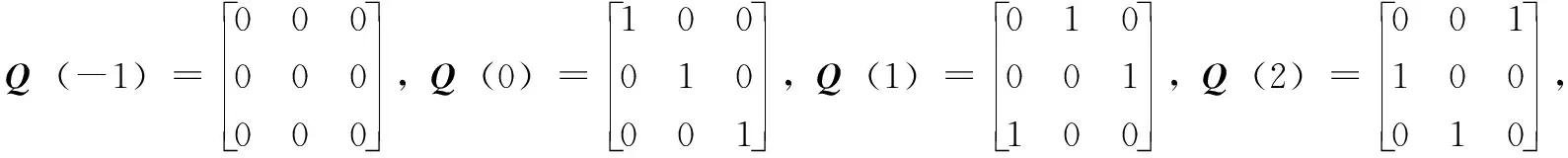
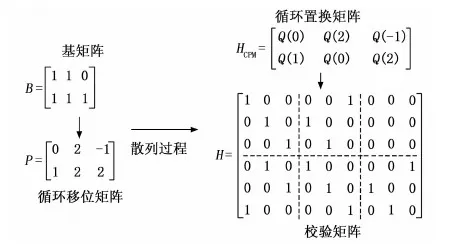
图1 QC-LDPC校验矩阵叠加构造过程

接下来，首先介绍基矩阵设计方案，然后构造循环系数表，在循环系数表的基础上对循环移位矩阵进行设计，然后通过叠加构造方法获取校验矩阵，最后对所设计的校验矩阵的误码率性能进行对比仿真。

1.1 基矩阵设计

在5G LDPC编码标准中，LDCP码的校验矩阵具有非常强的稀疏性，这种稀疏性质使得LDPC码非常适合于各种迭代译码算法并能获取近似最优的译码性能。5G LDPC码基矩阵的设计本身具有一定的稀疏性，如图2中LDPC码的Tanner所示，若不具有稀疏性，则变量节点与校验节点之间的连接线将非常的密集，导致译码复杂度急剧增加，稀疏性则是在保证译码性能变化不大的情况下降低迭代译码算法的复杂度，因此节点的度分布特性将是基矩阵构造的重要指标。

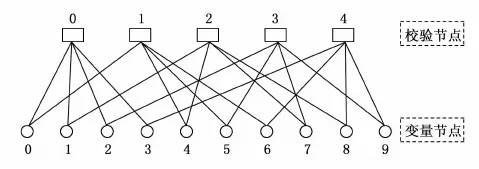
图2 列重为2、行重为4的(10, 5)LDPC编码Tanner示意图

LDPC码采用迭代译码时在低信噪比区域，即瀑布区域具有译码门限效应，当信噪比高于此门限值时，译码的可靠性将会有大幅度提升，而该门限值的取值将取决于节点的度分布，通过码分析工具可预测校验矩阵的译码门限。基于度分布的外信息转移(EXIT，extrinsic information transfer)图具有使用简单以及预测精准的优点，基于基矩阵设计的LDPC码具有一定的结构化，因此可采用基于图结构的EXIT(P-EXIT，protograph-based EXIT)技术。结合上述分析，在构造基矩阵的过程中，可通过采用P-EXIT技术计算基矩阵的译码门限，从中寻找具有最优译码门限值的基矩阵[14]。

1.2 循环系数表设计

在循环移位矩阵设计之前，首先需要获取循环系数表，循环系数表可通过代数法来进行设计。目前，有多种代数法都可用于构造满足行列(RC，row-column)约束的循环系数矩阵[15]，其中，RC约束指任意两行(或两列)不会有超过一个相同位置上同时为非零元[13]，满足RC约束条件所设计的校验矩阵，其迭代译码通常具有较好的性能。本小节采用基于素域来构造循环系数表。

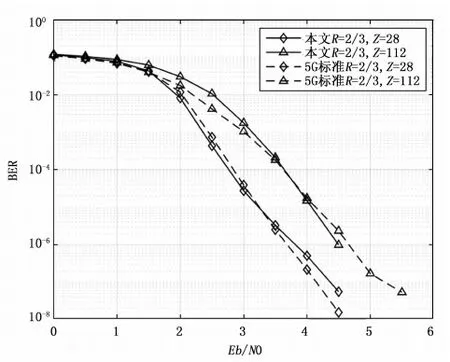
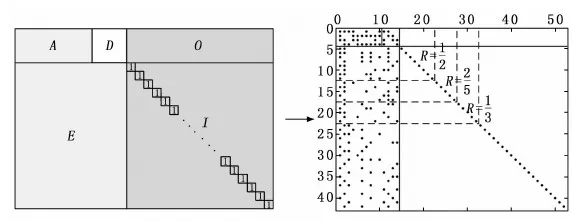
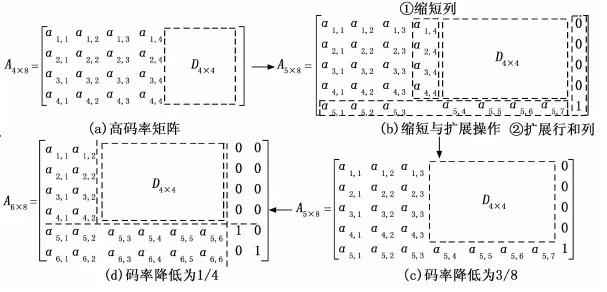
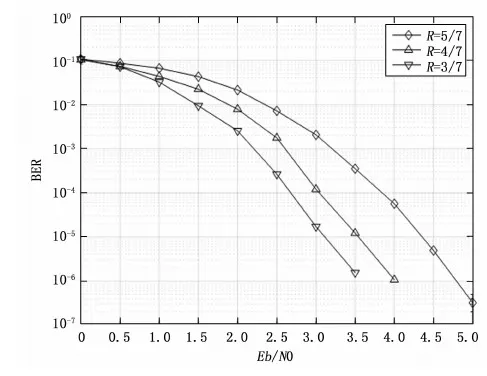
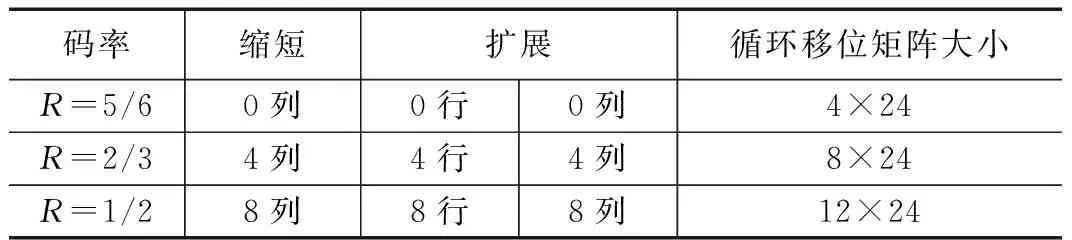
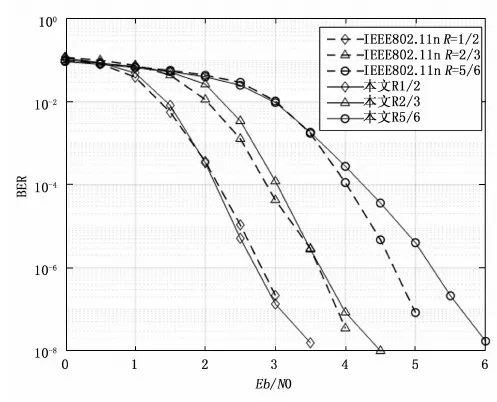
假设GF(q)是包含q个元素的Galois域[16]，考虑q为素数的情况，GF(q)={0,1,…,q-1}，其中元素的加法和乘法可直接进行“模q”运算。a为GF(q)中其中一个本原元，用a的幂次可表示GF(q)中所有的元素：a-∞,a0,a1,…,aq-2，通过“模q”可获得GF(q)中所有的元素。因此，对于0≤m,n

Tcc=[tk,l]=[αik×αjl](modq)

(1)

Tcc=[tk,l]=[αik±ηαjl](modq)

(2)

Tcc=[tk,l]=[ηαik+αjl](modq)

(3)

或者

Tcc=[tk,l]=[logα(αik±ηαjl)](modq)

(4)

Tcc=[tk,l]=[logα(ηαik+αjl)](modq)

(5)

基于上述素域构造方法构造的循环系数表每一行所有的元素都是不相同的，任意两行(或两列)在任何位置上没有相同项。为了获取性能更好的LDPC码迭代译码性能，所设计的LDPC码其Tanner图应尽量避免短环的存在，即没有长度为4的环和尽量少的长度为6的环，如图2所示，其中黑色粗线即为所形成的长度为6的环[17-18]。基于上述的构造方法获取到循环系数表后，若基矩阵满足RC约束[19]。

1.3 循环移位矩阵设计

获取到循环系数表Tcc后，可据此进行循环移位矩阵P的构造，如何从Tcc中选取最优的循环系数来构造性能较好的循环移位矩阵，需要有一个评判标准。

LDPC码的Tanner图是一种图形化的针对LDPC码校验矩阵的完全表示方法，这种表示方法有助于译码算法的描述，LDPC码的译码算法可描述为Tanner图中校验节点与变量节点之间的信息交互，迭代译码的有效性取决于Tanner图的结构特性，短环会降低LDPC码所使用的迭代译码算法的性能，因此，可通过不同环长的数量并对不同环长分配以不同的权重来形成一个评判标准从Tcc中进行筛选，最终形成性能最优的循环移位矩阵。

设循环移位矩阵为P=[pi,j]0≤i

(6)

其中:0≤iz

根据上述的环存在的充要条件，可以对所设计的循环移位矩阵根据不同环长、不同移位尺寸Z的条件下满足式(6)的组数进行计数，并设置相应的权重使不同移位尺寸、不同环长条件下具有可比性，由此获取的环加权平均数(WANC，weighted average number of cycles)如下式所示：

(7)

其中:NZ为所支持的不同移位尺寸的数量，ωZ(i)为所支持的不同移位尺寸的权重，Nc为环长种类数目，ac(j)为不同环长的权重，N(i,j)为不同移位尺寸，不同环长条件下计算出满足式(7)的组数。由于环长越短对LDPC迭代译码性能的影响越大，因此在考虑权重时应随着环长的增加权重越低，由此可得出，W(P)值越大，性能越差。

为简化算法，循环系数表Tcc列数与循环移位矩阵的列数相同，这样可以行为单位进行筛选。在基矩阵已知的情况下，先对前两行根据标准进行判断，然后逐行添加，为下一节多码率的设计做铺垫。由Tcc根据判断标准W(P)来设计的循环移位矩阵算法流程如算法1所示。

算法1:循环移位矩阵构造

输入：基矩阵B，B大小为mb×nb，循环系数表Tcc，Tcc大小为m×nb

输出： 循环移位矩阵P

1) 初始化：W*=+∞

2) /***先对前两行进行设计***/

3)repeat

4)fori=1:mdo

5)P*[1,:]=B[1,:]⊙Tcc[i,:]+B[1,:]-ones[1,:]

6)forj=1:m(j≠i)

7)P*[2,:]=B[2,:]⊙Tcc[j,:]+B[2,:]-ones[1,:]

8)ifW(P*)

9)P=P*，W*=W(P*)

10)endif

11)endfor

12)endfor

13)/***对后面逐行设计***/

14)fork=3:mbdo

15)forj=1:m(不包括已选行)

16)P*[k,:]=B[k,:]⊙Tcc[j,:]+B[k,:]-ones[1,:]

17)ifW(P*)

18)P=P*，W*=W(P*)

19)endif

20)endfor

21)endfor

22)returnP

根据上述算法来获取性能最优的循环移位矩阵。

1.4 矩阵叠加构造

如图1所示，叠加构造的过程既是CPM到校验矩阵H的过程，该过程也是从LDPC码到QC-LDPC码的过程，校验矩阵H是由多个大小为基于移位尺寸的Z×Z的循环子矩阵构造而成。CPM的构造是由循环移位矩阵确定的，确定过程中以单位矩阵为基础，即循环移位值为0时，CPM中对应的元素为Q(0)，当循环移位值为t时，CPM中对应的元素为Q(t)，其对应的子矩阵是在单位矩阵的基础上每行均右移t位，此外，Q(-1)对应的是全零矩阵，最终通过叠加构造的校验矩阵H的大小为(mb·Z)×(nb·Z)。

接下来，对所提方案与算法进行有效性验证。首先按照1.1节基矩阵设计所提方案利用P-EXIT技术进行大小为4×12的基矩阵的构造，然后根据1.2节通过代数法及式(4)进行循环系数表的设计，令GF(q)中q为素数241，7为GF(241)中其中一个本原元，以此设计大小为227×12的循环系数表，通过从循环系数表中随机选取12个元素作为集合S1，剩余的除0和1以外的元素作为集合S2，将两集合中的元素根据式(4)进行计算，获取循环系数表Tcc。

下面在已设计好的大小为4×12的基矩阵的基础上，对Tcc以行为单位进行选取，组成迭代译码性能最优的与基矩阵大小相同的循环移位矩阵。循环移位矩阵设计过程中通过对Tcc进行行遍历并根据式(7)进行判断获取最佳行使译码性能达到最优。本次验证过程选取的移位尺寸Z=112，在固定移位尺寸下，式(7)可简化为下式：

(8)

通过式(8)考虑环长为4、6、8的情况，按照多次测试的经验，三种环长相对应的权重分别为1 000、100、1。

基于上述流程，获取到的循环移位矩阵P如下所示：

P=

根据循环移位矩阵P可获取CPM，再根据移位尺寸进行叠加构造，最终获取到大小为448×1 344的校验矩阵H448×1344，码率R=2/3，信息位长度为896。然后利用同样的方法获取相同大小、移位尺寸Z=28的循环移位矩阵，通过叠加构造最终获取到大小为112×336的校验矩阵H112×336。对获取到校验矩阵进行编码，本文所有仿真中信道噪声均为二进制输入加性高斯白噪声(BI-AWGN，binary input additive white gaussian noise)，并通过和积算法(SPA，sum-product algorithm)进行译码，最大迭代次数为50。 根据所上述方案设计的校验矩阵与5G LDPC编码标准中的校验矩阵性能对比仿真图如图3所示。

图3 所设计方案与5G标准方案的性能对比仿真图

图3中，在码率统一为R=2/3条件下，移位尺寸分别为Z=112、Z=28情况下进行误比特率仿真，同时与5G LDPC编码标准中相同码率下，相同移位尺寸误比特率仿真结果进行对比。经过1×105帧次仿真，每帧大小与需编码的信息位长度相同，结果显示，上文所述校验矩阵设计方案所得仿真结果与5G标准中对应条件下的仿真结果大致相同，证明了设计方案的有效性。

2 固定码长条件下的多码率QC-LDPC码设计方法

根据算法1中循环移位矩阵的构造过程是逐行构造的，这为固定码长条件下的多码率QC-LDPC码的设计中针对循环移位矩阵的行列变化提供操作方法。在卫星广播系统中为保证系统的可靠性和可用性通常采用固定的有效载荷大小，对应固定的码字长度，但是具有灵活的码率。现有的5G LDPC编码标准中，根据码率的不同，相同信息位长度编码后的码字长度不同。本节针对天基物联场景，参考5G LDPC码设计方案并在此基础上通过基矩阵和循环移位矩阵的设计来构造具有类Raptor结构的具有固定编码长度条件下实现不同码率的QC-LDPC校验矩阵。

2.1 类Raptor结构稀疏校验矩阵设计

参考5G LDPC码标准中校验矩阵H的设计，5G标准中的校验矩阵是具有类Raptor结构的稀疏矩阵。Raptor码是LT码的一个扩展，Raptor码相对于LT码增加一个纠错码作为外码用以解决LT码可靠性较低的问题[21]，借鉴Raptor码的结构生成的校验矩阵易于编译码的硬件实现，且可基于类Raptor结构的校验矩阵直接进行编码，不需再将校验矩阵转换为生成矩阵。此外，参考5G LDPC码标准中的基矩阵的设计结构进行基矩阵的设计，实现循环移位矩阵的稀疏化，最终通过叠加构造形成的具有更加稀疏性的校验矩阵，大大降低了译码算法的复杂度。

Raptor结构是以高码率校验矩阵为基础进行拓展，扩展后的校验矩阵会伴随着码率的逐步降低，以此来实现降低码率的效果，该结构非常适用于多码率的设计。类Raptor结构的稀疏校验矩阵的设计如图4所示。

图4 类Raptor结构校验矩阵设计及BG2中不同码率分布图

其中，图4中左图为类Raptor结构整体组成划分，右图为5G LDPC标准中BG2的点图以及实现不同码率的扩展示意图。矩阵D是固定的大小为4×4的矩阵；O为全零矩阵；I为单位矩阵；[AD]共同构成了高码率矩阵，在其基础上向E逐行扩展，可以将高码率看成外码，扩展的校验矩阵看成内码进行串行级联以实现降低码率的设计。根据上图可看出，实现不同码率的过程是向下并向右进行矩阵拓展，导致不同码率下最后通过编码获取的码字长度不同。接下来，以高码率校验矩阵为基础通过缩短和扩展操作来实现固定编码长度条件下实现多码率的设计思路。

图5 基于缩短和扩展的固定码长多码率设计过程图

2.2 基于缩短与扩展条件下的多码率设计

所提出的多码率设计方案仍然采用类Raptor结构，在构造过程中加入了缩短和扩展操作来实现不同码率条件下，编码后码字拥有固定的长度。假设所给校验矩阵H的大小为M×N，则其码率可表示为R=(N-M)/N。构造过程中，缩短操作可通过减少信息位的列数来降低信息长度，但仅通过缩短操作就会改变编码后码字的长度，为了实现固定码字长度，通过扩展操作可在高码率条件下通过添加列向量和行向量来实现，同时实现了降低码率的效果。扩展操作已在标准5G LDPC码的多码率设计过程中有所体现，标准中，在[AD]高码率矩阵的基础上进行行向量和列向量扩展。

图5展示了通过缩短和扩展操作来实现多码率以及编码后码字长度固定的效果，操作后的矩阵结构符合类Raptor结构的设计。根据图5所示，A4×8矩阵码率为R=1/2，D矩阵为固定矩阵，保持不变。通过缩短操作，去掉靠近D矩阵左侧的列向量，为保持矩阵编码后码字长度不变，并保持类Raptor结构的设计，在D矩阵右侧添加列向量，可参考BG2矩阵所示，所添加列向量是固定的且具有一定的规律，即最后一位为1，其他全部为0。接下来在矩阵底部添加行向量，行向量的添加过程是基于2.2节基矩阵的设计与2.3节循环移位矩阵的设计过程进行添加，根据码率的不同，缩短列数与添加列数与行数也发生相应的变化，最终实现不同码率下的循环移位矩阵。

图5中，子图(a)中矩阵A4×8即为码率为R=1/2的高码率矩阵，子图(b)演示了缩短与扩展的操作过程，最终得到子图(c)中矩阵A5×8，码率为R=3/8，实现了码率的降低，子图(d)为再次缩短一列，扩展一行及一列的过程，实现码率为R=1/4的矩阵A6×8，码率得到进一步降低，但是编码后的码字长度并未改变，并符合类Raptor结构。

2.3 固定码长条件下的多码率QC-LDPC码设计仿真分析

根据1.1节基矩阵的设计方案以5G LDPC编码标准中BG2为蓝本对其前14列重新进行设计，然后根据1.2节令GF(q)中q为素数769，11为其中一个本原元，构造大小为753×14大小的循环系数表，最后根据1.3节设计方案构造大小为4×14的循环移位矩阵形成高码率母本，形成高码率母本后可根据2.2节的缩短和扩展方案进行固定编码长度的多码率设计，根据码率的不同，缩短与扩展的大小不同。根据上述过程形成的高码率母本码率为R=5/7，再根据缩短和扩展方案缩短两列信息位并进行相应扩展形成码率为R=4/7、R=3/7的循环移位矩阵，令移位尺寸Z=28时进行仿真对比，如图6所示。

图6 固定码长不同码率条件下的仿真图

经过1×105帧次仿真，每帧大小与需编码的信息位长度相同情况下进行仿真对比，仿真结果显示，码率越小，性能越好，可证明所提方案的有效性。由于所选移位尺寸较小，不同码率之间的性能差距并不是很大。

3 不同码率条件下的仿真结果

IEEE802.11n标准的编码特点保持了编码后码字长度的固定，并根据行数增加实现不同码率，且可实现相对较小的码字长度。综合第1～2节阐述的构造固定编码长度条件下多码率QC-LDPC设计过程，结合天基物联场景下短码传输的特点，通过上述过程进行不同码率的设计，并与IEEE802.11n标准中相同移位尺寸，对应码率条件下进行性能仿真对比。仿真过程中信道噪声采用BI-AWGN，译码方案采用SPA译码算法，最大迭代次数为50。

为与IEEE802.11n标准中不同码率条件下进行性能对比，参照标准中校验矩阵大小，结合上述构造过程进行循环移位矩阵的构造。所构造的高码率循环移位矩阵大小为4×24，通过缩短和扩展操作实现不同码率。

表1 不同码率条件下缩短与扩展大小列表

循环移位矩阵构造过程中，令GF(q)中q为素数769，选取本原元为11，移位尺寸Z=54，经过1×105帧次仿真，每帧大小与需编码的信息位长度相同，仿真结果如图7所示。

图7 不同码率条件下的性能仿真对比图

仿真结果显示，本文所提方案均能达到误比特率低于10-7，可有效满足卫星通信高可靠性的要求。除在高码率高信噪比情况下性能有所下降外，其他条件下与IEEE802.11n标准相同码率条件下性能相差很小，所提方案能达到预期的编码效果。

4 结束语

卫星通信网络与地面通信网络融合发展是未来通信网络发展的趋势，卫星通信的发展目前正处于加速阶段。天基物联场景将从广域范围内进行数据采集与指令交互，该场景数据传输的特点为小数据传输，因此，本文聚焦于短码传输，借鉴5G LDPC编码标准类Raptor结构，进行基矩阵设计与循环移位矩阵设计。此外，参考DVB-S2X标准编码特点通过缩短与扩展操作实现固定编码长度下的多码率设计。本文提供了基本的设计思路并验证其有效性，为天基物联场景下信道编码构造提供思路，但在基矩阵设计过程中还可根据码率调整进一步优化，循环移位矩阵的设计也可将多个移位尺寸条件考虑进去进行优化，缩短与扩展的操作对于整个矩阵的影响还需要进一步深入研究，这些内容可作为未来研究的方向。