基于多普勒变化率估计的载波跟踪算法

马 瑞，耿虎军，王西夺，陈韬亦

(中国电子科技集团公司 第54研究所，石家庄 050081)

0 引言

在卫星通信系统和临近空间飞行器中，卫星和接收机之间存在复杂的相对运动，其引起的多普勒频移也会随时间不断地变化[1]，通常会带来多普勒频移和多普勒频率变化率。Ka频段和Q/V频段射频信道的逐渐成熟导致收发双方的多普勒效应越来越大。复杂的噪声干扰环境也会影响信号的跟踪效果[2]。

接收端与发射端相对运动复杂，所处噪声环境也存在不确定性，使得收发双方的多普勒效应变大，并且存在较大的波动。在扩频通信系统中，对信号的跟踪通常分为两部分，即：伪码跟踪和载波跟踪。由于伪码速率较小，受到多普勒效应的影响不大，而载波多普勒不可忽略，通常既有多普勒频率又有多普勒变化率，所以载波跟踪问题就变成了扩频通信系统中的信号跟踪问题的主要部分。

对于含有多普勒频率变化率的载波跟踪问题，通常使用三阶锁相环对载波进行跟踪，但是热噪声会引起锁相环的相位抖动，其均方根值表达式如下：

(1)

由上式可知，当噪声条件、积分时间等确定时，锁相环相位抖动的误差只与环路带宽有关，为了降低相位抖动带来的误差，保证载波跟踪的准确度，锁相环应设置较窄的环路带宽[3]。但是在大动态的环境下，较窄的环路带宽可能会因为动态应力过大而导致环路失锁，因此研究大动态、低信噪比下的载波跟踪方法十分重要。

国内外理论界关于载波跟踪问题的研究源于锁相环的发展思想。锁相技术是实现相位锁定的一门技术，锁相环是完成这一技术的相位负反馈调节系统[2]。自1932年Debellescize提出了同步检测理论，首次开启了对锁相环的描述，提出锁相概念，并且将其应用于无线电信号的同步接收环节；1940年锁相技术在电视机同步装置中首次得到应用，用于改善电视机的成像具有抑制外界噪声干扰的作用；第二次世界大战期间，锁相环也逐渐应用于战争中，随着战争对同步的要求越来越高，也推动了锁相技术的发展，在此之后越来越多的反馈理论得到了大大的应用。五十年代，Jaffe R和Rechtin E首次将锁相技术应用于导弹的跟踪中；六十年代，锁相理论有了进一步的发展，锁相环的研究进入非线性理论分析环节；随着半导体集成技术的成熟，在1965年，第一块PLL集成电路芯片出现。随后数模混合的锁相环电路以及全数字锁相环电路相继出现，PLL性能一步步逐渐提高。

为解决大动态、低信噪比环境下的载波跟踪问题，宦昱采用了基于模糊控制的锁频环辅助锁相环的载波跟踪结构，对两环的环路增益进行调节[3]，但是环路的增加会对信号的噪声条件要求很高，也会使跟踪环节变得不稳定；齐航天等人以传统卡尔曼滤波为基础，使用锁相环和无迹卡尔曼两种工作模式应对不同跟踪环境，并在环路中添加计算判别器实时控制环路输出[4]；关磊等人利用联合导频与Viterbi译码幸存处理的载波同步方法，首先利用最小二次均方误差准则和导频序列对信号进行粗略估计，再将信号输入锁相环进行载波跟踪[5]；宋青平等人针对当前含有多普勒变化率载波的跟踪问题，通过对比分析锁频环辅助锁相环方法的局限性，提出了一种更高阶锁频环辅助高阶锁相环的跟踪结构，通过一系列理论推导与分析，设计出一套适用于三阶锁频环辅助四阶锁相环的环路参数，并通过仿真验证了该方法的有效性，并在此基础面进行改进，通过切换环路的模式，提高跟踪精度[6]；刘永桦等人通过短时傅里叶变换结合最小二乘拟合算法估计信号频率及变化率辅助三阶锁相环对载波进行跟踪[7]；王旭东等人在大频偏的背景下，介绍了一种基于FFT辅助COSTAS环的载波同步技术，能够跟踪较大范围的多普勒频率偏移[8]，但是未考虑大多普勒变化率的存在；文献[9]对低信噪比下的微弱信号使用四阶锁相环进行跟踪，但是随着环路阶数的增加会逐渐为跟踪带来不稳定因素；文献[10]对比了卡尔曼滤波与锁相环相结合的载波跟踪方法和锁频锁相环相结合的方法，表明了在低噪声环境下卡尔曼滤波算法的优越性；文献[11]提出了一种自适应载波跟踪算法，在载波跟踪环路中引入模糊控制器，自适应调整环路参数；文献[12]利用载波相位和符号定时联合估计的结果辅助三阶锁相环跟踪；文献[13]针对高动态环境下跟踪失锁的问题，提出了变带宽的自适应跟踪算法，通过感知动态环境的变化，自适应地对带宽进行调整；文献[14]针对高动态的载波跟踪问题，利用了开环估计与闭环跟踪相结合的方式，并利用锁频环辅助锁相环对载波进行精确估计；文献[15]将粒子滤波作为核心算法实现了在无线光通信场景下的载波恢复跟踪功能；文献[16]在精确制导武器、临近空间飞行器等应用场景下，研究了B1C信号导频分量QMBOC信号的接收处理；文献[17]分析了传统锁频鉴相器的一步延迟效应等弊端，提出了一种极大似然估计器辅助锁相环的载波跟踪算法，在响应速度、抗干扰性能方面优于传统算法；刘艺等人利用开环最大似然估计和扩展卡尔曼滤波跟踪算法解决了无人机、弹导运动目标间的稳定通信线路的问题，客服了传统环路不稳定的问题,能够在低载噪比下稳定工作且跟踪频率误差小,可快速实现高动态环境下载波跟踪[21]；林文兴则分析了卫星信号的多普勒频移及其变化率非常大引起跟踪环路动态应力过大而失锁的问题，提出了一种将卡尔曼滤波理论与粒子滤波理论引入环路的结构设计，以突破传统跟踪环路性能上的局限，并仿真验证了可行性[22]；张玉设计出一种基于免疫粒子群优化粒子滤波的载波跟踪算法，采用适应非线性系统的粒子滤波方法来对载波的相位、频率、频率一阶变化率和二阶变化率这4个参数进行估计，并考虑粒子滤波本身存在容易出现粒子退化和样本贫化的特点提出了免疫粒子群优化粒子滤波算法对其进行改进，并仿真验证了可行性[23]；综上所述，以上论文都在大动态、低信噪比的信号载波跟踪问题上做了研究，跟踪算法的计算量、结果的稳定性以及跟踪的稳定性是这类载波跟踪的共性问题，因此本文着眼大动态、低信噪比下的载波跟踪问题。

本文提出一种适用于大动态、低信噪比的载波跟踪算法。该算法采用信号动态估计辅助三阶锁相环的载波跟踪结构，并且在此基础上考虑符号速率，消除数据对载波恢复的影响。改进后的算法可以实现对大动态载波的稳定跟踪。

1 多普勒频率分析

低轨卫星与地面站之间的复杂的相对运动[14]会引起收发双方之间存在多普勒效应，假设相对运动状态为：

(2)

其中:v0为收发双方相对运动的初速度，a为为加速度，a′为加加速度，那么其引起的多普勒频移为：

(3)

其中:fc为接收信号的载波频率，φ为接收信号与相对运动的夹角。根据实际运动状态，相对加加速度不是引起巨大多普勒频移的主要原因，其二阶变化率相对较小，不是引起动态应力误差的主要原因[12]，因此接收信号的多普勒频移可表示为：

Δf=f0+at

(4)

带来的相位变化可表示为：

(5)

在采样率为fs的条件下接收信号可表示为：

(6)

其中:k为采样点，A为信号幅值，D(k)为原始数据，n(k)为复数形式的高斯白噪声。

2 理论分析

本文针对大动态、低信噪比的环境，设计出一种载波跟踪的方法。整个过程分为两部分：信号动态估计和三阶锁相环跟踪，第一部分又分为两部分，即多普勒变化率估计和多普勒频率估计。首先使用延迟相关的FFT算法对多普勒变化率进行估计并补偿，接下来对补偿信号进行FFT分析，估计多普勒频率并补偿；然后利用三阶锁相环对补偿后的信号进行跟踪。整个过程如图1所示。

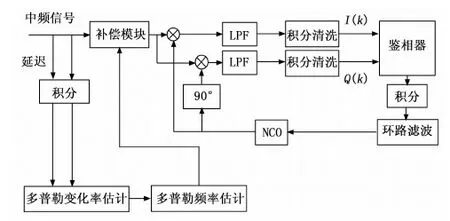
图1 跟踪结构图

2.1 信号动态估计

本文使用的信号动态估计算法，首先将信号进行延迟相关运算，消除信号中的其他未知量的影响，再对这个信号进行FFT分析得出变化率的估计值，对原始信号的变化率进行补偿后，设置FFT 分析的分辨率大于观测时间内频率的变化量，信号在这段时间内近似平稳，进行FFT分析得出多普勒频率估计值，此算法的结构如图2所示。

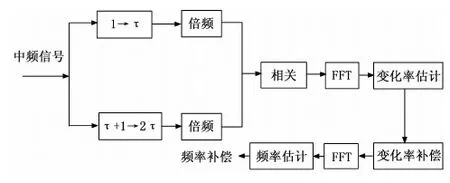
图2 信号动态估计结构图

2.1.1 多普勒变化率估计

对于信号多普勒频率的估计通常使用基于FFT的频偏估计技术，FFT是离散傅里叶变换的快速算法，可以将一个信号变换到频域，那么即可在FFT分析的频谱图中读出信号的频率成分。应用条件是在这段观测时间内信号频率保持恒定[14]，那么可将这段观测时间内的峰值点作为这段区间的载波频率估计值。FFT估计频偏的原理如下：

1)对接收信号进行去调制操作，消除数据影响；

2)对去数据的信号进行N点DFT可得：

(7)

3)对DFT的结果取峰值：

(8)

那么，该峰值对应的横坐标即代表信号中的频率分量。那么可以计算出频率的估计值：

(9)

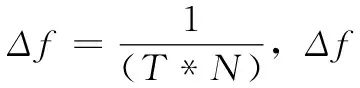
但是在本文的大动态环境中，接收信号存在较大的多普勒变化率，在短时间内多普勒频率变化巨大，而基函数e-j2πft只能将频偏为2πf分量的信号估计出来，不符合基于FFT估计技术的适用条件。而且过大的数据速率也要考虑去调制后的数据速率。如果忽略多普勒变化率的影响直接对接收信号进行FFT分析，如图3所示，设置信号多普勒频移为2 000 Hz，多普勒变化率为150 kHz/s，在63 dBHz的载噪比下对信号进行FFT分析，分析时间长度为0.01秒。

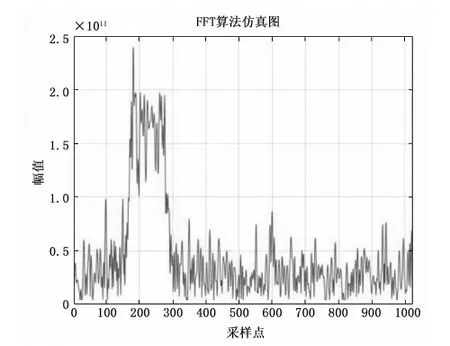
图3 接收信号的FFT仿真图

由于观测区间内信号的频率不是稳定不变的，所以其频谱也不是一个单峰谱[14]。当信号含有e-j2πat2分量时，无法实现完全补偿，经过傅里叶变换频谱能量无法集中，呈能量分散状态，导致了频率估计失效。

所以本文将信号进行延迟相关运算，消除其他未知量的影响，在BPSK调制体制下，接收信号r(k)以及延迟τ个点后的信号可表示为：

r(k)=AD(k)exp(j*φ(k)+n(k)

(10)

r(k+τ)=

AD(k+τ)exp(j*φ(k+τ))+n(k+τ)

(11)

倍频后：

r1(k)=A2D2(k)exp(j*2φ(k))+n2(k)

(12)

r1(k+τ)=

A2D2(k+τ)exp(j*2φ(k+τ))+n2(k+τ)

(13)

A4exp(j*2(φ(k+τ)-φ(k)))+(n2)*(k)n2(k+τ)

(14)

由上式可知，当延迟点数τ确定时，延迟相关函数是一个只含未知量a的复正弦信号，并且含有噪声项，其相位可以表示为：

(15)

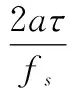
(16)

通过计算上式可得出多普勒频率变化率a的估计值，且估计值的精度与延迟时间有关，并且要考虑实际估计的信号符号速率的因素。并且噪声在载波相关的过程中也进行了相关，实际仿真与工程中要考虑对信号进行一定的累积减少噪声的影响。

2.1.2 多普勒频率估计

多普勒变化率补偿后的信号仍存在过大的多普勒频率，后续三阶锁相环跟踪要求初始多普勒频率近似环路带宽，但在低信噪比的环境下，要求锁相环的环路带宽尽可能小从而降低噪声对环路的影响。为缓解这一冲突，在多普勒频率变化率补偿后增加多普勒频率估计补偿部分。多普勒变化率补偿后，信号中还存在较小的多普勒变化率，若通过设置FFT的分辨率，使其大于信号频率在观测时间内的变化量，那么信号在这段时间内可以近似看作平稳信号。根据变化率余量，选取合适的FFT分辨率就能得出多普勒频率的估计值。

2.2 载波跟踪

经过估计、补偿后的信号，进入载波跟踪部分，假设进入跟踪环节的信号为r2(k)，结合前面分析的相对运动状态，可将信号表示为：

(17)

其中:f1为多普勒频率余量，a1为多普勒变化率余量。

在跟踪环路中，由本地数控振荡器NCO产生两路本地载波信号，并且相互正交，将其与接收信号相乘，将结果进行积分清洗，累积后的信号I、Q输入到鉴相器，得到误差信号，经过环路滤波器输出一个稳定的控制信号，输入到NCO，从而闭环达到对NCO的频率控制。设NCO产生的本地载波为：

s(k)=exp(j2π(fi/fs)k)

(18)

本地载波与接收信号分别相乘，通过低通滤波器滤除高频项，并积分得：

I(k)=A1D(k)cos(2π(Δf/fs)k)

(19)

Q(k)=A1D(k)sin(2π(Δf/fs)k)

(20)

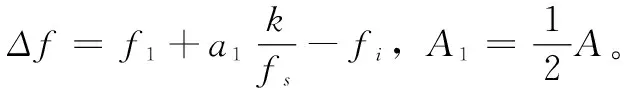
鉴相器采用反正切鉴相器，鉴相结果为：

(21)

3 仿真分析

经过捕获环节，跟踪环节接收到的信号等效为BPSK调制体制的正交I、Q信号，符号速率为1 Mbps，初始载波多普勒变化率跟踪范围为[-150 kHz/s，150 kHz/s]，初始载波多普勒频率跟踪范围为[-2 kHz，2 kHz]。在MATLAB平台，构造大动态、低信噪比的信号环境，设置采样率为100 MHz，数据速率为1 Mbps，载噪比为63 dBHz，初始多普勒变化率为150 kHz/s，多普勒频率为2 000 Hz，进行跟踪仿真。仿真共分为两步：信号动态估计仿真、载波环路跟踪。

3.1 信号动态估计仿真

3.1.1 变化率估计仿真

设置延迟时间为0.01秒，即延迟点数为1 000 000。在估计过程中，考虑1 Mbps的符号速率和63 dBHz的载噪比，首先对信号在一个数据内进行一次积分，将信号速率降到1 MHz。为消除数据的影响，对结果进行倍频操作，再进行40点积分，将结果补零再进行1 024点FFT分析，此时的分辨率为24.4 Hz，分析结果如图4所示，峰值的横坐标为124。

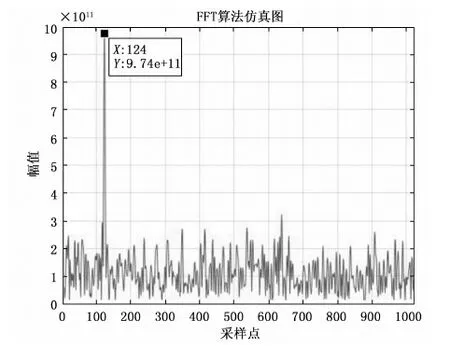
图4 延迟相关FFT仿真图

将上述仿真参数代入上述推导可得出a的估计值为150.146 5 kHz/s，误差约为146.5 Hz/s。

由此可见，使用这种延迟相关FFT的方法可以在低信噪比的环境下，将信号的多普勒变化率估计出来。进行的一系列积分操作也在一定程度上提高了信号的信噪比。

在参数未知的情况下，当接收信号的多普勒变化率范围为[-150 kHz/s，150 kHz/s]时，若使用分段搜索的方法对多普勒变化率进行估计，以200 Hz/s为步进，每次搜索进行一次FFT分析，至少需要进行1 500次FFT分析。而使用延迟相关的FFT算法，只需要进行一次相关运算和一次FFT分析即可实现对多普勒变化率的估计，大大降低了搜索运算量、估计结果更加精确并且更易于工程实现。

3.1.2 频率估计仿真

多普勒变化率补偿后的信号其变化率为146.5 Hz/s，多普勒频率为2 000Hz，在100 MHz的采样率下，同样考虑在不跨数据的前提下积分降速，进行100点积分。将降速后的信号进行倍频操作，消除了数据符号的影响，进一步降速处理，做40点的积分，对结果补零后进行1 024点的FFT分析，此时FFT的分辨率为24.4 Hz；在0.01秒的观测时间内频率的变化量为1.465 Hz，变化量小于分辨率，所以可以认为信号在这段时间内是平稳信号。FFT仿真结果如图5所示。

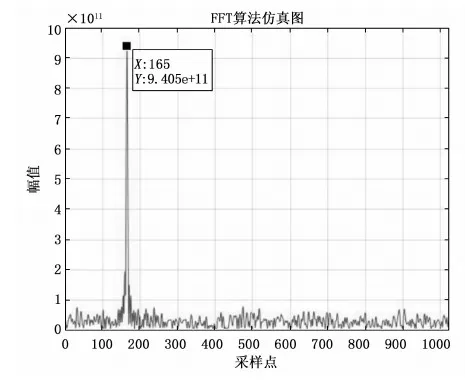
图5 补偿后信号的FFT仿真图

通过由仿真图5可知，峰值点的横坐标为165，并且由上述推导可知，估计值即对应FFT的峰值。那么可以算出多普勒频率的估计值为2 001.95 Hz，初始值为2 000 Hz，误差为1.95 Hz。

3.1.3 估计精度分析

改变延迟相关的点数进行仿真，可得变化率估计值如表1所示。

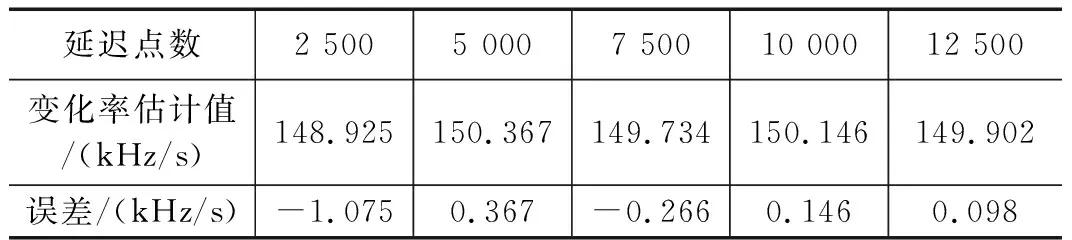
表1 延迟点数-估计误差关系

随着相关点数的增加，估计误差逐渐减小，多普勒变化率估计值逐渐稳定在150 kHz/s，但是仿真要在估计效果和耗费时间上做平衡，所以本算法需要根据实际工程选取合适的延迟点数。

3.2 载波跟踪环路仿真

经过多普勒频率及变化率估计后，多普勒频率和变化率已得到了补偿，信号的动态大大缩小。经过补偿后的多普勒频率为2 Hz，多普勒变化率为146.5 Hz/s，设置锁相环的环路带宽Bl为50 Hz，仿真时间为0.8 s。

将一个数据时间长度内累加后的实部、虚部信号输入到鉴相器中，反正切鉴相后输出相位差，将此时的相位差进行积分，进一步降低速率，提高信噪比。

误差结果输入环路滤波器，环路滤波器结果控制数控振荡器产生本地载波信号。对接收信号的跟踪情况如图6～7所示。

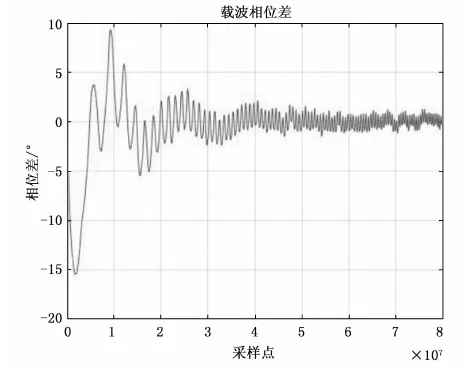
图6 载波环路输出相位差

将仿真结果多普勒频率余量2 Hz和多普勒频率变化率146.5 Hz/s代入前面的公式可知接收信号的多普勒频率表达式为：fi=2+146.5t。

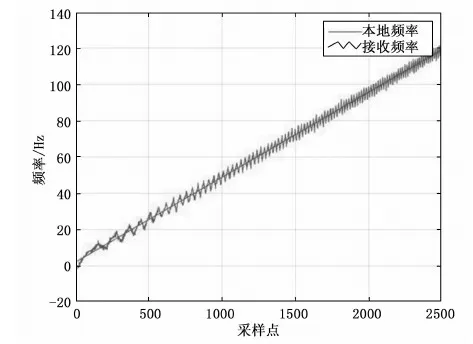
图7 载波环路输出频率-接收频率

由仿真图像可知，鉴相误差在大约在60 000 000个采样点即0.6秒后，稳定在0°附近，本地频率在0.6秒后也基本稳定在接收频率附近。

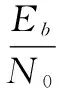
(22)

计算可得理论误码率为2.2%。

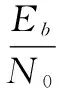
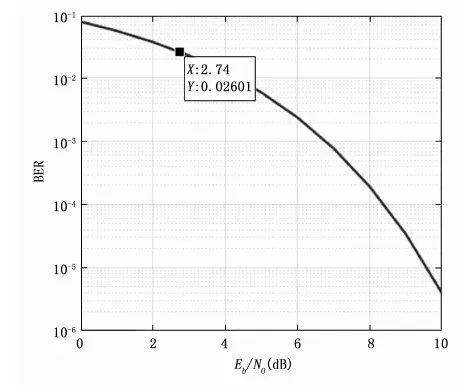
图8 BPSK下噪声环境对解调性能的影响

综上所述，使用这种算法首先对信号的动态进行估计补偿，再进入环路进行跟踪，可以在信号进入环路前有效缩小信号的动态，将150 kHz/s、2 000 Hz的信号跟踪上且通过计算解调损失在0.3 dB以内，且整个流程耗时0.7 s以内。

4 结束语

本文针对大动态、低信噪比的环境，提出了一种由延迟相关FFT算法和FFT分析相结合辅助三阶锁相环的载波跟踪方法，通过仿真验证了该方法的可行性，为接收机载波跟踪模块的改进提供了依据。

通过仿真验证，在63 dBHz的载噪比下，符号速率为1 Mbps，跟踪变化率为150 kHz/s时，这种方法可以在0.7秒内实现载波稳定跟踪，且误码率在2.6%左右，解调损失在0.3 dB以内。与传统的信号估计算法相比，该算法只需要进行一次相关运算和一次FFT分析即可得出变化率估计值，大大减小了搜索计算量；与单一的三阶锁相环跟踪相比，在进入锁相环之前缩小了信号的动态，补偿后的信号输入环路中使得环路入锁更快，并且降低了解调误码率；与锁频环辅助锁相环跟踪算法相比，该算法更加简单稳定，易于工程实现。

但是在进行相关运算的同时对噪声的加强也是不可忽略的，在信噪比极低的情况下，噪声会影响动态估计结果，从而影响后续锁相环跟踪。由此可见，本算法仍有待改善，接下来将更加注重考虑卫星通信系统的真实环境，在更低的信噪比下对此算法进行完善，设计出一套适应极低信噪比环境的仿真参数，实现极低信噪比下对大动态载波的稳定跟踪。