后续使用年限对既有建筑安全性鉴定的影响
叶旻笺,王梁亚,吕源芳
(1.中冶建筑研究总院(上海)有限公司,上海 200433;2.兖矿能源集团股份有限公司,山东邹城 273500)
1 引言
GB 50292—2015《民用建筑可靠性鉴定标准》[1](以下简称《民建可靠》)作为既有建筑安全性检测鉴定评定的重要依据之一,其规定构件承载能力评定是结构安全鉴定评级中第一层级,将抗力作用效应比R/(γ0S)的大小作为评定构件安全性等级的依据(其中,R 为结构构件的抗力;S 为结构构件的作用效应;γ0为结构重要性系数),评定结果分为au级、bu级、cu级和du级4 个等级。其中《民建可靠》第5.2.2 条规定,结构规定抗力作用效应比中抗力及荷载效应均按现行设计规范执行,但由于现行规范中各类参数如荷载分项系数、活载标准值等明显提高,造成既有结构安全性鉴定结果较差,多数构件评级为cu级甚至du级,而根据现场调查情况,构件仍处于正常使用状态,对鉴定工作造成困惑。
2022 年4 月1 日开始执行的GB 55021—2021《既有建筑鉴定与加固通用规范》[2]在既有结构安全性检测鉴定要求中,对既有结构的安全鉴定提出剩余设计工作年限的条件,其中对既有建筑在进行结构安全鉴定时,在明确后续使用年限的同时,应按不低于原建造时的荷载规范和设计规范进行验算,即安全性鉴定设置了不低于原设计规范的底线。但在实际检测鉴定工作中,后续使用年限确定在时间边界存在一定交叉,不同后续使用年限建筑在地震力计算方式上存在差异,给结构验算分析增加了复杂性。因此,针对上述问题,本文依据GB 50023—2009 《建筑抗震鉴定标准》[3]及GB 50068—2018《建筑结构可靠性设计统一标准》[4]等规范标准,结合GB 55021—2021《既有建筑鉴定与加固通用规范》对不同分类的建筑的地震作用折减要求,对于既有建筑根据后续使用年限的不同,分析得出不同的可靠性或失效概率。
2 不同后续使用年限下的可靠指标
2.1 失效概率与可靠指标的关系
结构安全的影响因素为R 和S,可采用状态函数Z=R-S来描述结构的安全状态。当Z=0 时,认为结构处于极限状态,可以衡量结构是否失效,那么结构的失效概率Pf可以描述为:
式中,P 为结构处于失效状态的概率。
因为一般抗力R 和荷载作用效应S 服从正态分布,那么状态函数Z 也服从正态分布,随机变量Z 的分布如图1 所示,失效概率等于图1 中阴影部分的面积。将图1 中0 到mZ的距离可以表示为可靠指标β 与标准差σZ的乘积,很明显可以看出,失效概率与可靠指标存在一一对应的关系,此时失效概率Pf为:
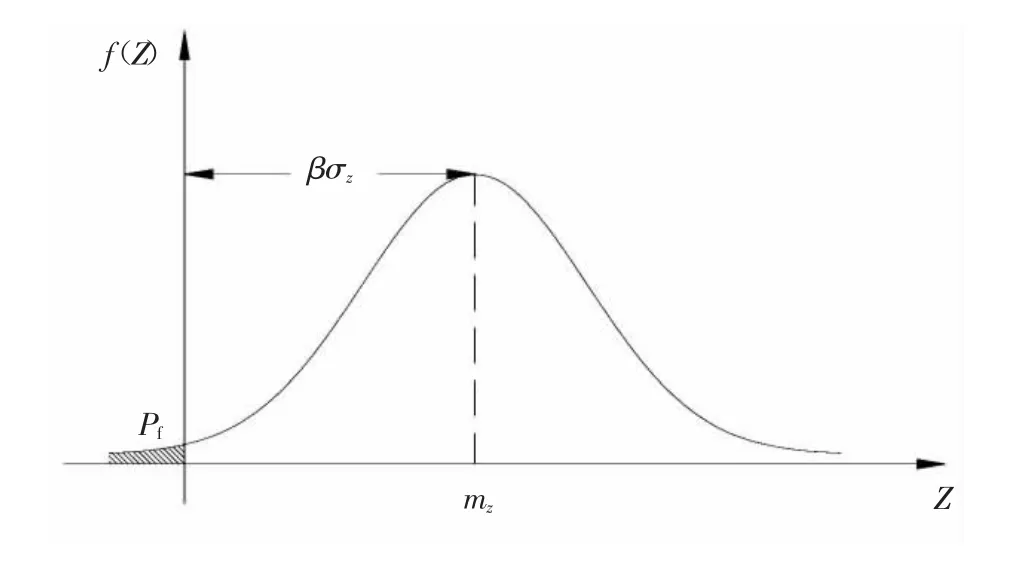
图1 随机变量Z 的概率密度函数
式中,mZ为状态函数Z 的平均值;σZ为状态函数Z 的标准差。
根据文献[5],将失效概率变化为标准化正态分布函数:
式中,Φ()为标准正态分布函数。
根据图1 中可靠指标的定义和式(3),可以得到失效概率与可靠指标的函数关系:
式中,Φ-1()为标准正态分布函数的反函数。
2.2 等失效概率的原则
GB 50068—2018《建筑结构可靠性设计统一标准》给出了设计基准期50 年时的可靠指标及失效概率,但未给出其他设计基准期下的可靠指标,如何考虑结构服役过程中的可靠度时变效应,是确定不同使用年限下的可靠指标是安全鉴定的关键。文献[6]分析了JCSS 概率模式规范中的年允许失效概率,通过将JCSS 模式规范的年允许失效概率换算为50 年使用年限的累积失效概率,其结果基本与我国统一标准中50 年基准期失效概率相同。按照不同后续使用年限下的失效概率与现行统一标准规定的失效概率相等的原则,就可以获得对应于不同后续使用年限的年失效概率,并由此确定考虑时变效应的可靠指标。不考虑抗力衰减的情况下,累积失效概率与使用年限成正比。根据上述假定,不同后续使用年限的失效概率增长线如图2 所示。

图2 失效概率增长线
Pf,t(T)表示基准期为t 年时,使用T 年的失效概率。由此可以确定,后续使用年限为30 年、40 年和50 年的失效概率随时间变化的直线,将3 个基准期下的失效概率换算到同一个时间维度(50 年),可得30 年、40 年后续使用年限的失效概率,按式(4)计算,可得到对应的可靠指标。
根据GB 50068—2018 《建筑结构可靠性设计统一标准》,50 年基准期、安全等级为二级时,延性破坏可靠指标为3.2,脆性破坏可靠指标为3.7。根据图2 及式(5),运用等失效概率的原则可以得到30 年、40 年后续使用年限对应于50 年基准期的失效概率及可靠指标(图2 中B 点、C 点),结果见表1。

表1 不同后续使用年限的失效概率及可靠指标
2.3 不同后续使用年限下的构件安全性分级
《民建可靠》将构件安全性按承载能力分为4 级:au级下限可靠指标大于或等于现行规范要求,即β≥β0,表征为抗力作用效应比R/(γ0S)大于或等于1;bu级的下限可靠指标为β0-0.25,大致相当于失效概率上升半个数量级,表征为抗力作用效应比R/(γ0S)大于或等于0.95;cu级的下限可靠指标为β0-0.5,表征为抗力作用效应比R/(γ0S)大于或等于0.9;du级的可靠指标β<β0-0.5,表征为抗力作用效应比R/(γ0S)小于0.9。参照现行鉴定标准,可将不同年限下的构件安全性按照βt、βt-0.25、βt-0.5 为界限分成au级、bu级、cu级和du级4 个等级,可在表1 的基础上扩充为不同后续使用年限下的各分级界限对应的可靠指标和失效概率,如表2 所示。
3 算例
根据表2 得到的不同后续使用年限下的可靠指标采用实用分析法计算,可以判断具体构件不同使用年限下的安全性鉴定分级。实用分析法的原理见文献[7],本文不再赘述,以下将通过一个算例验证构件安全性的分级。
假设混凝土简支梁安全等级为二级,恒载作用下的弯矩标准值Gk=50 kN·m,活载作用下的弯矩标准值Qk=50 kN·m,截面抗力为Rk=122.2 kN·m。恒载为标准正态分布,活载为极值Ⅰ型分布,截面抗力R 为对数正态分布。则构件的极限状态为:
式中,λR为抗力分项系数。
根据《建筑结构设计统一标准》[8]钢筋混凝土受弯构件的统计参数,截面抗力R 的变异系数VR=0.10,平均值与标准值的比值KR=1.13;根据文献[9]恒载的变异系数VG=0.070,平均值与标准值的比值KG=1.060,活载的变异系数VQ=0.233,平均值与标准值的比值KQ=0.524。后续使用年限为50 年时,根据表2 按照延性破坏,au与bu界限的可靠指标为3.2,失效概率为0.000 69。以下按照实用分析法求Rk与λR:
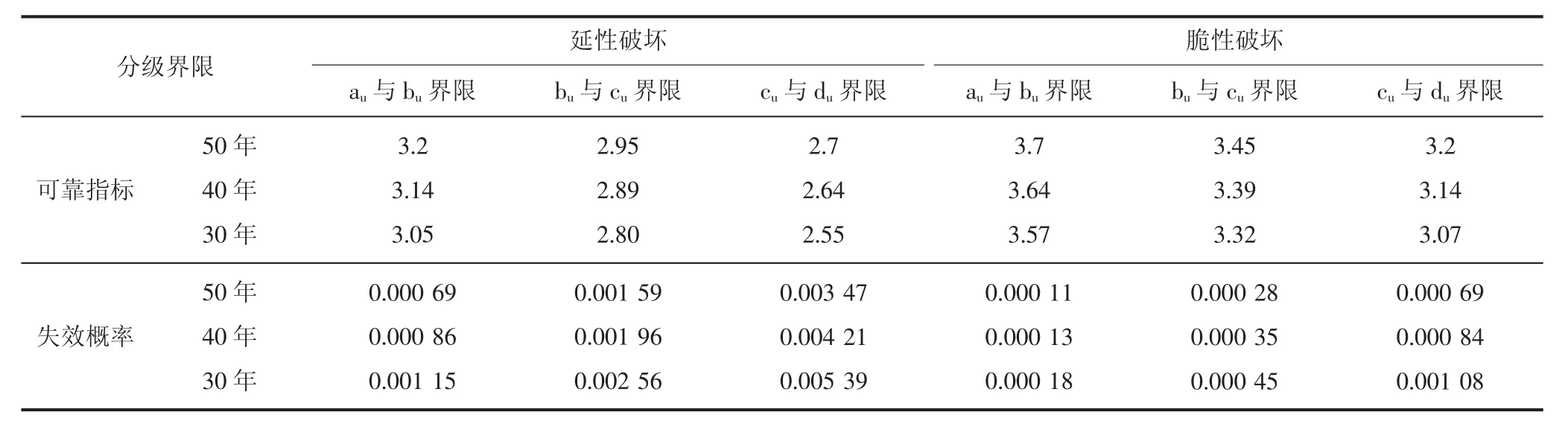
表2 按构件安全分级的失效概率及可靠指标
将式(11)~式(13)代入式(14),可得关于mR的一元二次方程,解方程可得mR=128.44 kN·m。由mR的值可计算得到Rk=mR/KR=113.66 kN·m,λR=1.14。同上步骤可求出不同可靠指标下的抗力作用效应比,结果列于表3。表3 中的50 年后续使用年限的抗力荷载效应比基本符合《民建可靠》,bu与cu界限、cu与du界限的R/(γ0S)均比规范略高,计算偏于安全。

表3 不同后续使用年限的构件安全性分级
混凝土梁截面抗力为Rk=122.2 kN·m 时,抗力荷载效应比为:
查表3 可知,不同后续使用年限对该混凝土梁的承载力安全评级有很大影响:当后续使用年限为50 年时,该混凝土梁安全等级为cu级;当后续使用年限为30 年时,该混凝土梁安全等级为bu级。由于现行鉴定标准规定构件的安全性等级取承载能力、不适于承载的变形或位移、裂缝或其他损伤等4个项目中的最低一级,由于鉴定标准要求按承载能力按现行规范进行验算,随着荷载分项系数、结构重要性系数、楼面活载标准值等提高,将构件按承载力评定等级降低,造成评级失真。文献[10]提出构件评级应根据现场调查结果结合计算分析进行综合评定。通过上述按时变可靠指标经过调整后,随后续使用年限的降低,构件的抗力荷载效应比也随之降低,结合现场调查情况,将对构件的安全评级更准确。
4 结论
本文从构件安全性分级的内核可靠指标出发,给出了不同后续使用年限的时变可靠指标,并结合实际案例,给出了不同后续使用年限构件的安全性鉴定结果。总结结论如下。
1)现行可靠性鉴定标准对构件按承载能力的分级未考虑按不同后续使用年限的折减,将会导致鉴定结果的失真,造成不提升后续使用年限的房屋的非必要加固量提升。
2)本文按照不同后续使用年限下的失效概率不变的原则,计算得到了不同后续使用年限对应的可靠指标。并在此基础上,结合现行可靠性鉴定标准构件承载能力安全性按可靠指标分级的内核,推导得到了30 年、40 年、50 年后续使用年限下按构件安全分级的失效概率及可靠指标。
3)通过算例,以上述失效概率及可靠指标,采用实用分析法计算出构件不同后续使用年限的构件安全性分级。计算结果显示,按50 年后续使用年限的构件安全性分级指标R/(γ0S)比现行标准略高,偏于安全。根据构件的实际R/(γ0S)指标,后续使用年限对构件的评级产生明显影响。

