全面思考 言必有据

赵小冬

在解题中，思考时要全面周到，表达时要言必有据，避开一些常见的误区.

误区一 忽视分类

例1 已知△ABC是等腰三角形. 若∠A = 40°，则△ABC的顶角度数是 .

错解：40°. 忽视∠A是顶角或是底角，造成了漏解.

正解：40°或100°.

误区二 忽视作辅助线的可行性

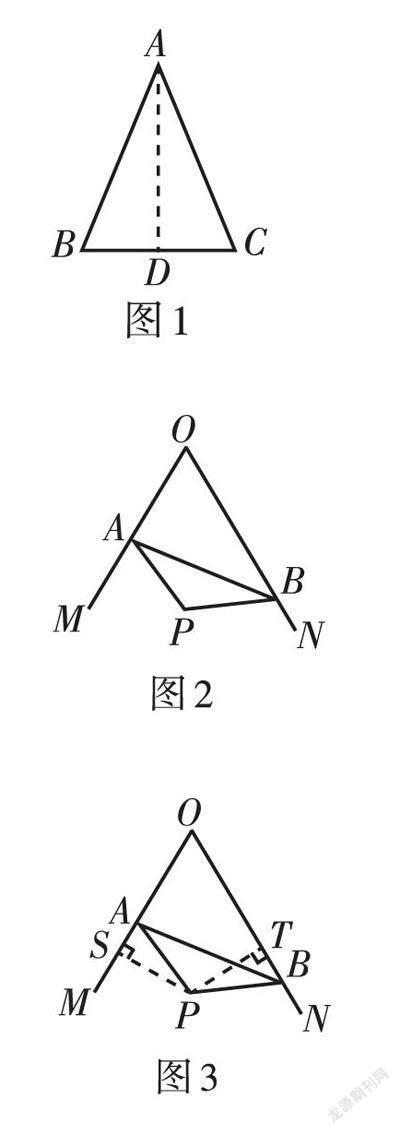
例2 如图2，在△ABC中，∠B = ∠C. 求证：AB = AC.

错解：过点A作BC的中垂线AD，垂足为D，则BD = CD. 再证明△ABD ≌ △ACD，得到AB = AC. 这种作辅助线的表述有问题，因为过点A作BC的垂线与中线，两线不一定重合.

正解：过点A作BC的垂线AD，垂足为D. ∵AD⊥BC，∴∠ADB = ∠ADC.

∵AD = AD，∠B = ∠C， ∴△ABD ≌ △ACD（AAS），∴AB = AC.

反思：作辅助线时，一般不能同时满足两个或两个以上的条件. 若要使所作辅助线同时满足两个要求，则作图时只能先满足其中一个要求，再证明它满足另一个.

误区三 忽视前提条件

例3 如图2，∠MON = 60°，点A，B为射线OM，ON上的动点（点A，B不与点O重合），且AB = [43]，在∠MON的内部、△AOB的外部有一点P，且AP = BP，∠APB = 120°. （1）求AP的长；（2）求证：点P在∠MON的平分线上.

错解：（1）AP = 4（过程略）；（2）∵AP = BP，∴点P在∠MON的平分线上.

这里的AP和BP不是点P到OM和ON的距离，不能运用角平分线的判定定理.

正解：如圖3，过点P分别作PS⊥OM于点S，PT⊥ON于点T，

∴∠OSP = ∠OTP = 90°.

∵∠SPT = 360° - ∠OSP - ∠O - ∠OTP = 120°，

∴∠APS = ∠BPT.

∵AP = BP，∴Rt△APS≌Rt△BPT （AAS），∴PS = PT，

∴点P在∠MON的平分线上.