基于改进密度峰值聚类算法的梨花密度分级
周桂红,孙乐琳,梁芳芳,张秀花
基于改进密度峰值聚类算法的梨花密度分级
周桂红1,2,孙乐琳1,梁芳芳1,2※,张秀花3
(1. 河北农业大学信息科学与技术学院,保定 071001;2. 河北省农业大数据重点实验室,保定 071001;3.河北农业大学机电工程学院,保定 071001)
精准判断梨花疏密程度是自动疏花的基础。为了更好地判断梨花密度,该研究提出了基于改进密度峰值聚类算法的梨花密度分级方法。该方法首先提取梨花位置坐标,获取需要聚类的数据点。其次,为了实现梨花图像的密度分级,针对原有密度峰值聚类算法在梨花密度分级中的不足,结合梨花密度分级需求,改进了对聚类中心的选取方式,通过4组局部密度和中心偏移距离分割阈值将决策图划分为4部分来选取聚类中心,分别对应高、中、低密度以及无需疏花处理等4个等级,实现了对疏密合理的梨花图像的准确分级。最后,针对只有团状分布、稀疏分布及大尺度特写的梨花分布聚类分级不准确的问题,改进了两点间的距离d参数的计算方法,统一梨花尺度大小和密度分级标准,对所有分布类型的梨花图像均能实现合理的密度分级。试验结果表明,该研究算法能够适应不同尺度大小的梨花图像,预测准确率为94.89%,密度分级准确率达到94.29%,可实现自然环境下局部花簇的密度分级,为机器智能疏花提供了技术支持。
图像识别;农业;聚类算法;密度分级;位置坐标;阈值;梨花
0 引 言
当梨花过于密集时,会造成果树养分的供不应求,适当疏花能够控制梨花密度,有效调节果树的养分供应,使果园保持稳产,提高果实品质[1]。人工疏花易疲劳、效率低且成本高,容易错过最佳的疏花时期,难以满足大型果园的疏花需求[2];采用化学疏花的方式,容易受到天气条件的影响,会对果树造成伤害,并且喷洒过程中对花朵强壮程度不加以区分,会导致疏花过度或疏花不足[3]。因此,快速准确地对不同梨花密度科学合理地自动化疏花,对提高智慧农业生产效率具有重要意义[4]。
自动化疏花包括2个关键技术:梨花识别与分割、梨花密度估计,梨花识别与分割是梨花密度估计的前提。基于传统图像处理方式的识别与分割方法多数依赖于颜色特征提取、阈值分割、边界分割和区域分割[5-8]。基于深度学习的目标检测与分割通常采用YOLO[9-10]、SSD[11]、Faster R-CNN[12]、Mask R-CNN[13-15]等算法来实现,采用优化网络结构、数据增强等手段提高花的识别与分割效果,对于复杂自然环境下果树花朵识别的研究已经较成熟[16-21]。WU等[22]利用通道剪枝的YOLOv4网络模型对不同品种的苹果花实时检测,具有较高的准确度和较强的鲁棒性。YOLOv4网络模型已经被验证可较好的用于自然环境下苹果花快速准确检测。
实现密度检测可有效判断花朵的密集程度,为疏花提供直观的判断依据。目前,密度检测的研究分为传统机器学习方法和深度学习方法。传统方法的密度检测在利用传统方法识别和分割花朵区域之后,根据连通域面积得到密度图。如KRIKEB等[23]使用不同的红色阈值分割花蕾(暗红色)与花朵(粉红色),比较花和花蕾面积来估测开花高峰期,绘制开花强度图。相较于人工目测,传统方法体现出一些优势,但对颜色、纹理等因素依赖性较强,受光照和背景噪声影响较大。基于深度学习的密度检测方法是在基于深度学习的花的识别与分割基础上得到密度图,有效避免了以上问题[24]。WANG等[25]提出一种基于全卷积网络(fully convolutional networks, FCN)的像素级苹果花语义分割技术,根据花像素和区域像素的占比获得密度图。虽然基于深度学习的语义分割效果较好,但需要训练大量像素级标注的数据集,标注复杂且耗时过长。
受交通拥堵程度估计和人口密度估计方法的启发[26],本文提出基于改进密度峰值聚类算法的梨花密度估计方法。在YOLOv4网络模型识别并定位梨花之后,通过本文方法首先获取梨花位置坐标,根据坐标值进行密度峰值聚类,然后改进了原算法中对聚类中心的选取方式,得到了高、中、低密度以及无需疏花处理等4个等级的聚类中心。此外,对两点间的距离d参数的计算方法进行了改进,统一梨花尺度大小,最终得到最佳密度分级结果,为自动化疏花提供研究基础。
1 数据采集与处理
1.1 数据采集
试验所用的梨花图像样本采自河北省保定市易县牛岗村河北农业大学研究基地,品种为3年生秋月,果园的栽培模式为南北成行,株距1.2 m,行距3.9 m。本研究于2021年4月18日梨花盛花期采集自然环境下的梨花图像,采样时间上午08:00-12:00,下午02:00-05:00。尼康相机距梨花约20~30cm垂直拍摄,拍摄图像原始格式为JPG,像素分辨率为4 000×6 000像素(2∶3)。图像采集时,采用随机方式挑选梨花多的枝条拍摄,采集图像包括顺光、逆光、不同角度和不同遮挡程度的花朵和花苞。
1.2 数据预处理
本文共采集382张梨花图像,为适应YOLOv4网络模型的最佳识别效果,将采集的图像随机裁剪成608×608像素,不足则进行填充,填充颜色为RGB(128,128,128)。裁剪之后随机去除天空、土地等不包含梨花目标的子图像,整理后共2 734张梨花图像,训练集∶测试集∶验证集= 7∶2∶1。采用LabelImg图像标注工具对梨花进行标注,标签为PearBlossom和Bud两种。
2 梨花密度分级方法
在深度学习网络模型识别并定位梨花位置之后,本文首先获取梨花坐标,然后利用改进密度峰值聚类算法进行密度分级,如图1所示。基于深度学习的梨花识别不作为本文的研究重点,而是将重点放在识别之后的坐标提取和密度分级。

图1 梨花密度分级流程
2.1 坐标提取
由于本文采用Pascal VOC2007的数据集格式,因此在YOLOv4网络模型预测梨花时可得到预测框的左上角坐标(left,top)和右下角坐标(right,bottom),如图2所示。在以为坐标原点,像素列数为横轴,像素行数为纵轴的像素坐标系中,坐标点(left,top)代表图像中第top行第left列的像素点,本文中提到的目标检测框的中心坐标,计算式如下:
height=bottom−top(1)
width=right−left(2)

注:横轴为像素列数,纵轴为像素行数。
Note: The horizontal axis is the number of pixel columns, and the vertical axis is the number of pixel rows.
图2 梨花坐标提取示意图
Fig.2 Diagram of extracting pear flower coordinates
2.2 密度峰值聚类算法
密度峰值聚类[27](density peaks clustering, DPC)算法是一种典型的基于密度的聚类算法,该算法不需要迭代,可一次性找到聚类中心。该算法有两个特征:聚类中心的密度比较大;不同聚类中心之间的距离相对较远。
具体的算法步骤如下:
1)已知数据集包含个样本点,计算任意两个样本点之间的距离d:

式中x和x分别表示第和第个样本点的坐标;dist(x,x)表示x和x两个坐标的欧式距离;表示维度;x和x分别表示维度上第和第个样本点的坐标值,,∈{1,2,…,}。
2)计算第个样本点的局部密度ρ:
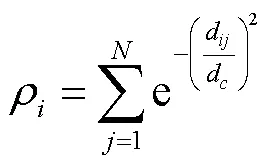
式中d表示截断距离,可指定。
3)计算第个样本点的中心偏移距离δ:
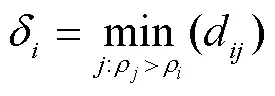
4)以ρ和δ分别为横纵坐标,画出横轴为局部密度,纵轴为中心偏移距离的决策图。
5)选出聚类中心和噪声点。
6)分配剩余点。
2.3 改进密度峰值聚类算法的密度分级
2.3.1 聚类方法的改进
决策图是DPC算法选取聚类中心的关键,在决策图中,普通点靠近轴,噪点靠近轴,可通过阈值选择值偏大且值比较大的点作为聚类中心[27]。原算法仅用一组阈值选取聚类中心,不能满足梨花密度分级的需求。因此,本文改用4组阈值来选取聚类中心。ρ、δ是一组高密度等级的分割阈值,分别表示高密度等级的局部密度阈值和中心偏移距离阈值,ρ、δ是一组中密度等级的分割阈值,分别表示中密度等级的局部密度阈值和中心偏移距离阈值,ρ、δ是一组低密度等级的分割阈值,分别表示低密度等级的局部密度阈值和中心偏移距离阈值,ρ、δ是一组无需疏花处理密度等级的分割阈值,分别表示该等级的局部密度阈值和中心偏移距离阈值,其中δ、δ、δ三者数值相同,ρ与最小局部密度min数值相同。该4组阈值的具体取值根据专家经验及反复试验的结果最终确定,选取不同等级聚类中心的阈值决策标准如图3所示。同一组阈值的聚类中心用同一种图案表示,代表同一等级;十字图案代表无需疏花处理的密度等级;另外三种图案则分别代表高中低三个密度等级。
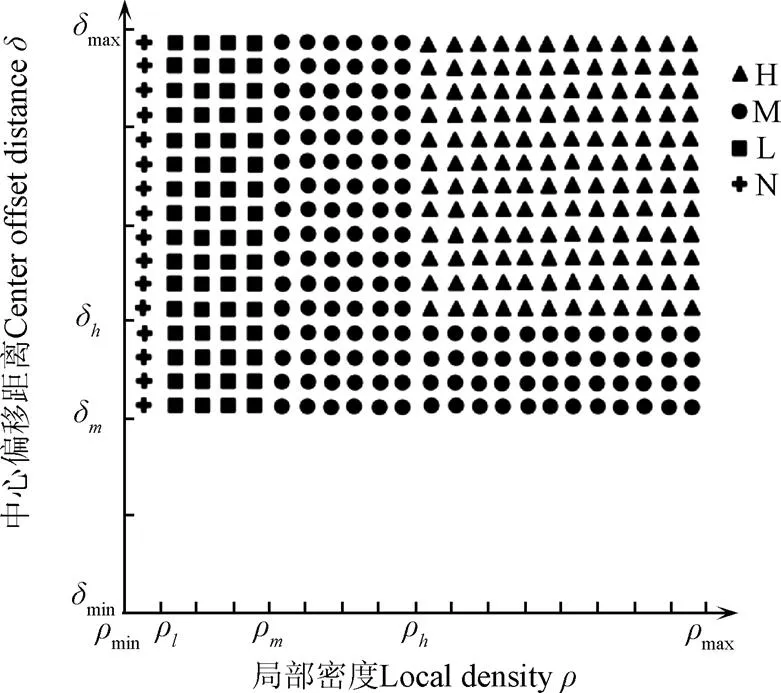
注:ρmin和ρmax分别表示最小和最大的局部密度,δmin和δmax分别表示最小和最大的中心偏移距离。ρh、ρm、ρl分别表示高、中、低密度等级的局部密度阈值,δh和δm分别表示高、中密度等级的中心偏移距离阈值。图例中H表示高密度等级,M表示中密度等级,L表示低密度等级,N表示无需疏花处理的密度等级。下同。
采用上述方法对梨花图像进行分级仍具有局限性,仅对疏密合理的梨花聚类分级准确,而对于团状分布、仅有稀疏分布以及大尺度特写的梨花分布聚类分级不准确,如图4所示。图4中分别展示了不同分布类型的原图图像、识别图像、聚类中心的决策结果图像以及不同密度等级的梨花坐标图像。其中聚类中心的决策结果图像横纵坐标分别为点的局部密度和中心偏移距离,并依据图3中的阈值决策标准确定了各个等级的聚类中心。不同密度等级的梨花坐标图像中各点坐标为提取出的梨花位置坐标,图中的数字代表相应聚类中心的编号。如图4a所示,依据聚类中心的决策结果图选出了编号为4和9的两个高密度等级聚类中心,以及编号为2和13的两个低密度等级聚类中心,之后在不同密度等级的梨花坐标图像中显示出聚类结果和密度等级。不同密度等级的聚类中心用不同形状的空心图案表示,作为疏花的切入点。不同密度等级的梨花坐标图中展示了密度等级和梨花位置分布的信息,在本文中代表密度图。
由图4中图像的密度分级结果可以看出,密度等级都为高、中、低密度以及无需疏花处理4个等级,显然团状分布图像、稀疏分布图像以及大尺度特写图像的密度等级与实际情况不符。团状分布应当作为一个整体花簇处理,而不应当分成过多聚类中心和密度等级,如图4b所示;稀疏分布应当呈现稀疏密度等级,不应当出现高密度等级,如图4c所示;大尺度特写图像梨花位置坐标相距较远,实则密集却造成稀疏分布的假象,如图4d所示。因此,需对识别图像做出统一尺度处理,同时确定统一的密度分级标准。
2.3.2 确定标准图像
为了确定合理的标准图像以及图3中4组阈值的具体取值,首先根据专家经验挑选出一批疏密合理的梨花图像进行试验,不断调整选取不同等级聚类中心的阈值决策标准,使得在该阈值下梨花图像的密度分级结果符合专家预期效果。通过试验发现,标准图像最大局部密度与最小局部密度的差值,即∆集中在1.1~1.8,最大中心偏移距离与最小中心偏移距离的差值,即∆集中在170~450,d集中在40~55;非标准图像即团状分布、稀疏分布、大尺度特写等图像∆集中在0.35~1.5,∆集中在60~320,d集中在25~85,虽然∆和∆与标准图像有交集,但两者没有同时满足标准图像的取值区间。因此,∆或∆太小均不适合作为标准图像:1)梨花呈团状分布时的取值集体偏大,的取值集体偏小,坐标点会紧密相邻,d的取值会偏小;2)梨花呈稀疏分布时的取值集体偏小,的取值集体偏大,坐标点会较分散,d的取值会偏大。因此,标准图像的选取应该满足:∆和∆的取值合理,和的取值不应集体偏大或集体偏小。根据以上原则,通过试验挑选出较合适的标准图像,如图4e所示。
2.3.3 参数d的改进
确定标准图像后,通过试验发现标准图像和4种不同分布类型的图像选取聚类中心的阈值存在一定规律,表1所示是对参数d改进前后的各阈值。由DPC算法可知,局部密度是判定密度大小的关键参数。从表1可以看出,改进前标准图像和疏密合理的图像的高密度阈值ρ分别为0.846和0.634,由于已知4种不同分布类型的图像中只有疏密合理的图像密度分级较合理,由此推断出,当某一图像的ρ值与标准图像相近时密度分级较合理。因此,本文控制4组选取聚类中心的阈值与标准图像的阈值一致,即在选出标准图像后,确定4种不同分布类型的图像与标准图像的ρ、δ、ρ、δ、ρ一致。由于标准图像是经过大量试验严格挑选的符合专家标准的一类图像,所以标准图像的参数处于标准范围内,具有参考价值。控制该组阈值与选定的标准图像一致,会使得4种不同分布类型图像的聚类中心和聚类簇重新选择,但不会改变、、d等参数值。由于其他标准图像与选定的标准图像所有参数都较接近,因此不会对其密度分级准确性产生影响。而对于不符合标准的梨花图像,控制该组阈值与选定的标准图像一致,可以强制聚类算法达到与标准图像相同的密度分级效果。该方式仅改善了尺度与标准图像相近的稀疏分布和团状分布的缺陷,但对于大尺度的梨花图像密度分级效果不理想。

注:图中不同的编号代表不同的聚类中心。不同形状的空心图案代表不同密度等级的聚类中心。
Note: Different numbers in the figure represent different cluster centers. Hollow patterns with different shapes represent cluster centers with different density grades.
图4 不同分布类型的梨花识别与梨花坐标的聚类结果
Fig.4 The results of pear flower recognition and pear flower coordinate clustering with different distribution types
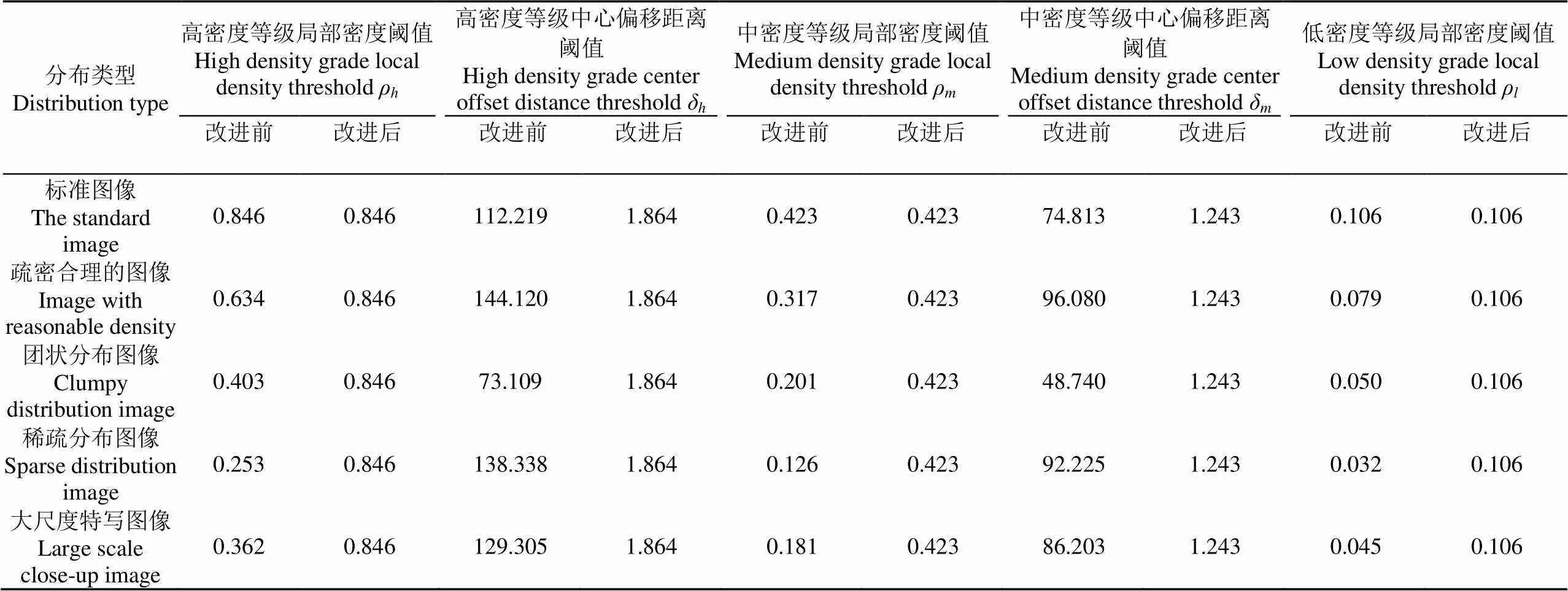
表1 算法改进前后不同分布类型图像的阈值
算法中d的值是根据“点周围到该点的距离小于d的点的数目记为W,W点占总点数的1%~2%[27]”来确定,因此两点之间的距离d对d起到影响作用,当d越大时d越大。而此时所有梨花图像的d参数值还受到梨花尺度大小的影响,因此在未统一尺度大小的情况下d的值没有对比意义。d与和都具有相关性,控制d值与标准图像一致,会影响局部密度和中心偏移距离值的大小,失去算法合理性,因此在此处对d不做处理。
特写图像梨花尺度较大,导致目标检测框的中心坐标点较分散、两点间的距离d较大等问题,造成稀疏的假象,因此需统一梨花尺度。首先,对d的计算方法进行改进,统一梨花尺度后再控制截断距离d与标准图像一致,从而实现尺度和密度分级标准的统一。d的改进思想:由于不同拍摄距离会产生不同尺度的梨花图像,采用YOLOv4深度学习网络模型识别梨花,目标检测框大小会随着梨花尺度大小变化而变化,因此,可通过目标检测框的大小来判定梨花尺度大小。本文引入所有目标检测框宽高的平均值vg参数,作为衡量梨花尺度大小的标准,将距离d改为统一尺度后的距离d′,计算式如下:


式中vg表示所有目标检测框宽高的平均值;表示图像中目标检测框个数;a和b分别表示第个目标检测框的宽和高。
如表2所示,将标准图像视为标准。改进后疏密合理的图像、团状分布图像、稀疏分布图像和大尺度特写图像相较于改进前d分别增大20.3%、增大6.5%、减小40.4%、减小19.4%;尺度分别增大4.9%、减小16.0%、减小12.1%、减小51.8%;最大局部密度值分别增大46.3%、增大78.8%、减小75.1%、增大151.3%。由于已知4种不同分布类型的图像中只有疏密合理的图像密度分级较合理,且从表2可以看出,疏密合理的图像和标准图像尺度大小最接近,由此也印证了统一尺度大小对密度等级划分合理性的必要性。
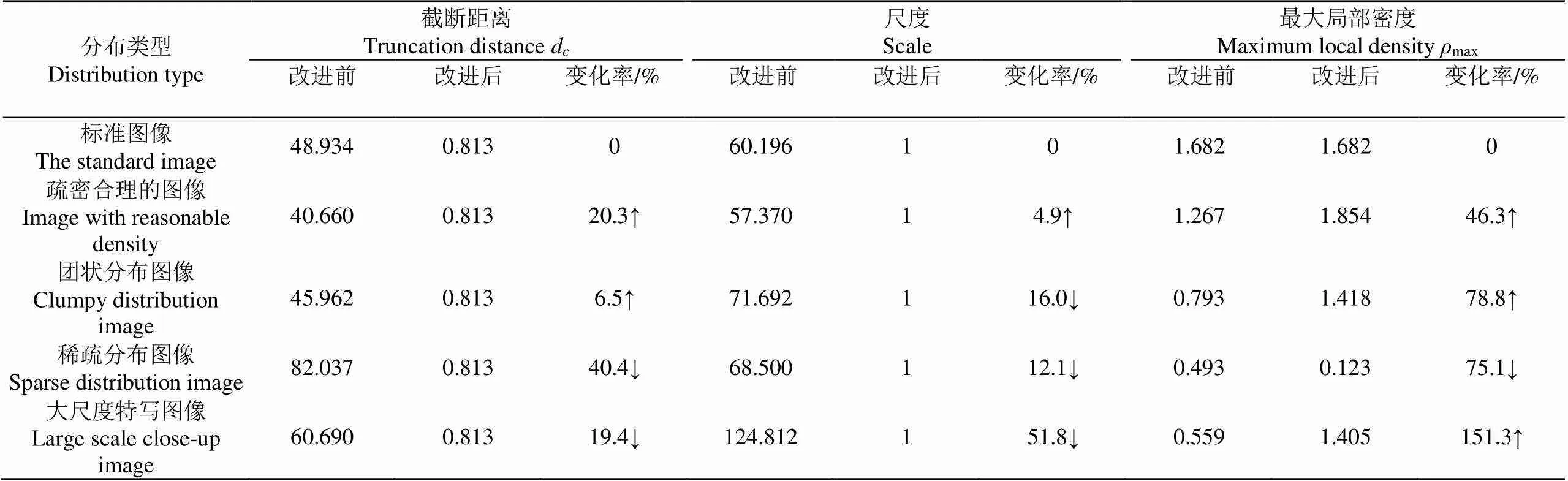
表2 算法改进前后不同分布类型图像的参数值变化率
注:将标准图像作为比较标准,↑和↓分别表示改进后的参数值相较于改进前增大和减小。
Note: Take the standard image as the comparison standard, ↑ and ↓ respectively represent the increase and decrease of the improved parameter value compared with that before the improvement.
3 试验设计
为了验证本文算法对梨花密度分级的有效性,采用随机抽样的方式从测试集中抽取20幅裁剪后的梨花图像样本,样本编号为0~19,并设计如下试验。
1)尺度大小对比试验:为验证本文算法中尺度的有效性,采用PS软件手工测量梨花尺度,以最接近梨花形状的圆面积大小作为梨花尺度大小,如图5a所示。测量所有花朵的尺度并求取平均值,将平均值作为整个花簇的测量尺度值,最终将测量结果与算法尺度值进行对比试验。

注:图5a中黄色圆的面积代表相应花朵的尺度测量值,红色轮廓围出的面积代表花簇面积测量值。图5b中所有花区域面积代表花面积测量值。所有测量面积的单位都为像素。
2)密度分级对比试验:为验证不同聚类算法对梨花密度分级的有效性,采用常用的K-means算法(K-means clustering algorithm)和DBSCAN(density-based spatial clustering of applications with noise)算法与本文改进后的DPC算法进行密度分级对比试验。由于K-means算法需设置初始聚类中心,为了减小随机初始化的误差,增大与本文算法的可对比性,将K-means算法初始聚类中心设置为本文算法所选出的聚类中心,聚类中心的密度等级也与本文一致。由于DBSCAN算法属于密度聚类,为了减小尺度差异对分级结果的影响,采用本文方法统一梨花尺度,然后采用与本文算法相同的标准图像数据集进行参数调整试验,最终依据专家经验及反复试验得出DBSCAN算法的初始参数:搜索半径为0.01,搜索半径内最小点数目(minimum number of points, MinPts)为3,当搜索半径内数据点数目大于MinPts设为高密度等级,等于MinPts设为中密度等级。此外,采用PS软件手工测量花簇密度作为密度分级评价指标,并对3种聚类算法进行评估。人工测量采用两种测量方式,其中测量密度1见式(9),人工模拟了尺度概念,融入了人工计数概念以及花簇面积概念,更适用于不同尺度大小的梨花图像;测量密度2见式(10)[23,25],由花面积与花簇面积的比值得出密度大小:


式中表示花簇中花朵个数人工计数值;花簇表示花簇面积测量值,单位为像素,如图5a所示;表示整个花簇中所有花朵测量尺度的平均值,单位为像素;花表示花面积测量值,单位为像素,如图5b所示。
4 结果与分析
4.1 尺度大小对比
对20张样本图像进行尺度大小对比试验,对比结果如表3所示。为了将测量尺度与算法尺度的单位统一成面积单位,将以vg为直径的圆面积作为算法尺度值。由表3可以看出,统计的尺度平均精度为94.89%。

表3 测量尺度值与算法尺度值统计比较
图6为测量尺度和算法尺度的1∶1比较图。从拟合结果可以看出,决定系数2值为0.996,统计误差在0.27%~12.44%之间,平均为5.11%。结果表明本文算法对尺度的预测精度较高,可有效实现对梨花尺度的估计。

图6 测量尺度值和算法尺度值的回归分析
algorithm scale value
4.2 密度分级对比
对20张样本图像中的单个花簇进行密度分级对比,共35组样本花簇。图7为两种不同测量方式的花簇密度对比曲线,图中两种测量密度曲线走势基本一致,说明两种测量方式可相互验证。但测量密度2的曲线波动性较小,其原因是:因遮挡或裁剪只剩下局部的花瓣,所以导致计量花朵面积偏小,部分测量密度2的数值偏小。

注:样本花簇编号的中间字母代表密度等级,字母前面的数字代表样本编号,字母后面的数字代表样本内的花簇编号。如0H1代表样本0中编号为1的花簇是高密度等级。
通过分析,选定测量密度1作为真实测量值,由图7可以看出,存在一个阈值区间[0.9,1.1]将测量密度1划分成高、中、低3个等级,测量分级结果如表4所示。除样本2和样本11中的两个花簇外,本文改进的DPC算法对剩余33个花簇等级的预测与测量分级一致,密度分级精确度达到94.29%。K-means算法和DBSCAN算法密度分级精确度分别达到94.29%和68.57%。K-means算法与本文改进的DPC算法密度分级精确度相同,但缺少自动选取不同密度等级聚类中心的算法步骤,随机初始化聚类中心对聚类结果影响较大且与密度无关,不利于梨花密度分级。DBSCAN算法对密度大小的计算方式缺乏连续性,对密度等级的划分不够精细。改进后的DPC算法密度分级精确度较高,且能够自动选取聚类中心和划分密度等级,从密度分级精确度和聚类中心选取方式两方面综合分析,本文改进的DPC算法效果最佳。

表4 测量分级与不同聚类算法分级的统计比较
注:测量分级依据测量密度1得出。H/M/L表示图中有三个花簇,密度等级分别是H、M、L。括号内数据表示将L等级误判为N等级个数,由于低密度等级无需疏花处理,因此将L等级误判为N等级可忽略不计。
Note: Measurement classification is based on measure density 1. H/M/L represents that there are three flower clusters in the image, and the density grades are H, M and L. The data in parentheses represents the number of L wrongly identified as N. Because the low-density grade does not require flowers thinning, it can be ignored when L is wrongly identified as N.
不同算法针对不同分布类型的梨花坐标的聚类结果如图8所示。K-means算法初始聚类中心用空心图案表示,并显示其编号,最终聚类中心用叉号表示。由于K-means算法对噪点敏感,当图中存在噪点时会影响聚类中心的最终迭代结果,与初始聚类中心偏离较大(图8a,图8b)。由于DBSCAN算法无需确定聚类中心,图中空心图案代表了核心点,并显示其编号,当某个数据点的搜索半径内数据点数目大于或等于MinPts时被称为核心点。DBSCAN算法对噪点具有鲁棒性,能够剔除噪点(图8a,图8b),但由于对密度等级划分不够精细,导致密度分级效果较差。如图8a所示,DBSCAN算法将大多数中密度等级的坐标点划分为噪点;如图8c所示,DBSCAN算法将高密度等级的坐标点划分为中密度等级。本文改进的DPC算法与改进前对比,团状分布图像被划分成一个密度等级,可作为一个整体花簇处理(图8a);稀疏分布只呈现低密度等级,符合稀疏密度图的特点(图8b);大尺度特写图像在改进之后只呈现一种高密度等级,与实际相符(图8c)。本文改进的DPC算法与其他聚类算法相比,具有帮助选取不同密度等级聚类中心的决策图,减小了随机初始化的误差;对噪点具有鲁棒性,能有效剔除噪点(图8a,图8b);密度计算方式具有连续性(式(5)),对密度等级划分更准确。
上述结果表明,在改进d参数的计算方法且控制ρ、δ;ρ、δ;ρ、δ;ρ、δ4组阈值以及d与标准图像一致之后,统一了梨花尺度和密度分级标准,梨花密度分级结果更准确合理。
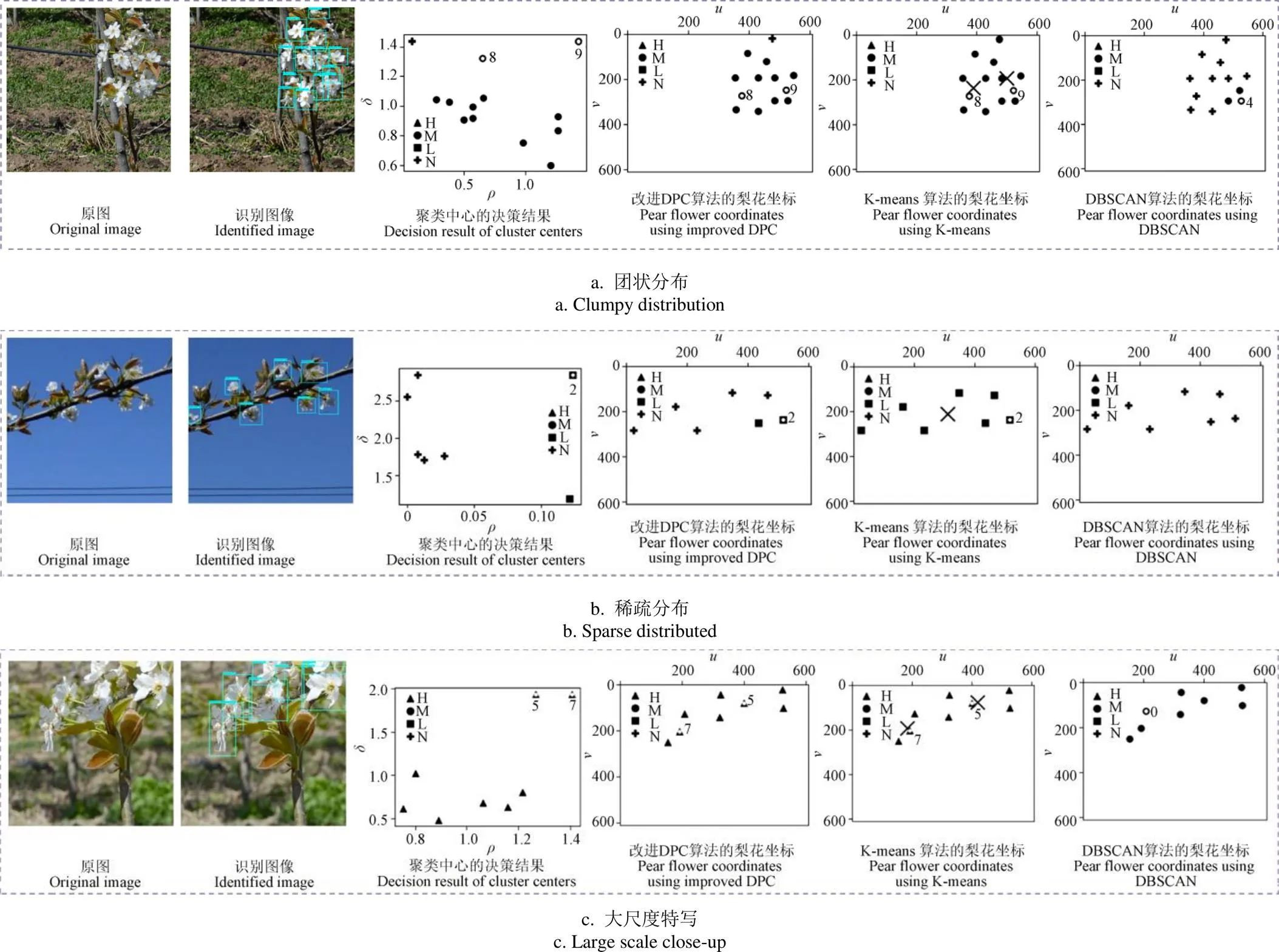
注:K-means算法中不同的编号代表不同的初始聚类中心,不同形状的空心图案代表不同密度等级的初始聚类中心,×代表最终聚类中心。DBSCAN算法中不同的编号代表不同的核心点,不同形状的空心图案代表不同密度等级的核心点。
5 结 论
本文提出基于改进密度峰值聚类算法的梨花密度分级方法,该方法在采用YOLOv4网络模型对图像预处理之后,提取梨花位置坐标,并利用坐标点进行聚类分析。然后为了实现梨花图像合理的密度分级,改进了聚类中心的选取方式和两点间的距离d参数的计算方法。
本文提出采用4组局部密度和中心偏移距离阈值来选取聚类中心,分别选出高、中、低密度和无需疏花处理等4个等级的聚类中心,初步实现密度等级的划分。本文采用改进后的d´参数来计算两点间的距离,避免了由于梨花尺度大小不同对密度分级结果造成的影响,实现了对疏密合理、团状分布、稀疏分布和大尺度特写4种分布类型的梨花图像的合理密度分级。结果表明,本文改进的密度峰值聚类算法对梨花尺度的预测准确率为94.89%,对梨花图像的密度分级准确率为94.29%。
[1] 李君,徐岩,许绩彤,等. 悬挂式电动柔性疏花机控制系统设计与试验[J].农业工程学报,2016,32(18):61-66.
LI Jun, XU Yan, XU Jitong, et al. Design and experiment of control system for suspended electric flexible thinner[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(18): 61-66. (in Chinese with English abstract)
[2] IWANAMI H, MORIYA-TANAKA Y, HONDA C, et al. A model for representing the relationships among crop load, timing of thinning, flower bud formation, and fruit weight in apples[J]. Scientia Horticulturae, 2018, 242: 181-187.
[3] 宋占丽,刁永强,拜热·居马洪,等. 不同疏花疏果剂对蜜脆苹果的疏除效果及成本分析[J]. 现代农业科技,2021(13):67-68.
[4] FARJON G, KRIKEB O, HILLEL A B, et al. Detection and counting of flowers on apple trees for better chemical thinning decisions[J]. Precision Agriculture, 2020, 21(3): 503-521.
[5] ZHANG C, XIE Y, LIU D, et al. Fast threshold image segmentation based on 2D fuzzy fisher and random local optimized QPSO[J]. IEEE Transactions on Image Processing, 2016, 26(3): 1355-1362.
[6] 杨陶,田怀文,刘晓敏,等. 基于边缘检测与Otsu的图像分割算法研究[J]. 计算机工程,2016,42(11):255-260,266.
YANG Tao, TIAN Huaiwen, LIU Xiaomin, et al. Research on image segmentation algorithm based on edge detection and Otsu[J]. Computer Engineering, 2016, 42(11): 255-260, 266. (in Chinese with English abstract)
[7] 彭明阳,王建华,闻祥鑫,等. 结合HSV空间的水面图像特征水岸线检测[J]. 中国图象图形学报,2018,23(4):526-533.
PENG Mingyang, WANG Jianhua, WEN Xiangxin, et al. Shoreline detection method by combining HSV spatial water image feature[J]. Journal of Image and Graphics, 2018, 23(4): 526-533. (in Chinese with English abstract)
[8] 刘双喜,孙林林,王震,等. 复杂背景下苹果树花量模糊聚类准确估测模型[J]. 中国农机化学报,2017,38(8):74-81.
LIU Shuangxi, SUN Linlin, WANG Zhen, et al. Fuzzy clustering accurate estimation model of apple tree flowers with complex background[J]. Journal of Chinese Agricultural Mechanization, 2017, 38(8): 74-81. (in Chinese with English abstract)
[9] 赵德安,吴任迪,刘晓洋,等. 基于YOLO深度卷积神经网络的复杂背景下机器人采摘苹果定位[J]. 农业工程学报,2019,35(3):164-173.
ZHAO Dean, WU Rendi, LIU Xiaoyang, et al. Apple positioning based on YOLO deep convolutional neural network for picking robot in complex background[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(3): 164-173. (in Chinese with English abstract)
[10] 杨军奇,冯全,王书志,等. 基于改进YOLOv4的田间密集小目标检测方法[J]. 东北农业大学学报,2022,53(5):69-79.
YANG Junqi, FENG Quan, WANG Shuzhi, et al. Method for detection of farmland dense small target based on improved YOLOv4[J]. Journal of Northeast Agricultural University, 2022, 53(5): 69-79. (in Chinese with English abstract)
[11] TIAN M, CHEN H, WANG Q. Detection and recognition of flower image based on SSD network in video stream[J]. Journal of Physics: Conference Series, 2019, 1237(3): 032045.
[12] 闫建伟,赵源,张乐伟,等. 改进Faster-RCNN自然环境下识别刺梨果实[J]. 农业工程学报,2019,35(18):143-150.
YAN Jianwei, ZHAO Yuan, ZHANG Lewei, et al. Recognition of Rosa roxbunghii in natural environment based on improved Faster RCNN[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(18): 143-150. (in Chinese with English abstract)
[13] HE K, GKIOXARI G, DOLLAR P, et al. Mask R-CNN [C]//Proceedings of 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy: IEEE, 2017: 2980-2988.
[14] 岳有军,田博凯,王红君,等. 基于改进Mask RCNN的复杂环境下苹果检测研究[J]. 中国农机化学报,2019,40(10):128-134.
YUE Youjun, TIAN Bokai, WANG Hongjun, et al. Research on apple detection in complex environment based on improved Mask RCNN[J]. Journal of Chinese Agricultural Mechanization, 2019, 40(10): 128-134. (in Chinese with English abstract)
[15] 邓颖,吴华瑞,朱华吉. 基于实例分割的柑橘花朵识别及花量统计[J]. 农业工程学报,2020,36(7):200-207.
DENG Ying, WU Huarui, ZHU Huaji. Recognition and counting of citrus flowers based on instance segmentation[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(7): 200-207. (in Chinese with English abstract)
[16] DIAS P A, TABB A, MEDEIROS H. Multispecies fruit flower detection using a refined semantic segmentation network[J]. IEEE robotics and automation letters, 2018, 3(4): 3003-3010.
[17] DIAS P A, TABB A, MEDEIROS H. Apple flower detection using deep convolutional networks[J]. Computers in Industry, 2018, 99: 17-28.
[18] TIAN Y, YANG G, WANG Z, et al. Instance segmentation of apple flowers using the improved mask R–CNN model[J]. Biosystems Engineering, 2020, 193: 264-278.
[19] SUN K, WANG X, LIU S, et al. Apple, peach, and pear flower detection using semantic segmentation network and shape constraint level set[J]. Computers and Electronics in Agriculture, 2021, 185: 106150.
[20] 尚钰莹,张倩如,宋怀波.基于YOLOv5s的深度学习在自然场景苹果花朵检测中的应用[J].农业工程学报,2022,38(9):222-229.
SHANG Yuying, ZHANG Qianru, SONG Huaibo. Application of deep learning based on YOLOv5s to apple flower detection in natural scenes[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2022, 38(9): 222-229. (in Chinese with English abstract)
[21] 孔英会,朱成诚,车辚辚. 复杂背景下基于MobileNets的花卉识别与模型剪枝[J]. 科学技术与工程,2018,18(19):84-88.
KONG Yinghui, ZHU Chengcheng, CHE Linlin. Flower recognition in complex background and model pruning based on MobileNets[J]. Science Technology and Engineering, 2018, 18(19): 84-88. (in Chinese with English abstract)
[22] WU D, LV S, JIANG M, et al. Using channel pruning-based YOLO v4 deep learning algorithm for the real-time and accurate detection of apple flowers in natural environments[J]. Computers and Electronics in Agriculture, 2020, 178: 105742.
[23] KRIKEB O, ALCHANATIS V, CRANE O, et al. Evaluation of apple flowering intensity using color image processing for tree specific chemical thinning[J]. Advances in Animal Biosciences, 2017, 8(2): 466-470.
[24] MADEC S, JIN X, LU H, et al. Ear density estimation from high resolution RGB imagery using deep learning technique[J]. Agricultural and Forest Meteorology, 2019, 264: 225-234.
[25] WANG X A, TANG J, WHITTY M. Side-view apple flower mapping using edge-based fully convolutional networks for variable rate chemical thinning[J]. Computers and Electronics in Agriculture, 2020, 178: 105673.
[26] YE T, ZHAO N, YANG X, et al. Improved population mapping for China using remotely sensed and points-of-interest data within a random forests model[J]. Science of the Total Environment, 2019, 658: 936-946.
[27] RODRIGUEZ A, LAIO A. Clustering by fast search and find of density peaks[J]. Science, 2014, 344(6191): 1492-1496.
Pear flower density classification based on improved density peak clustering algorithm
ZHOU Guihong1,2, SUN Lelin1, LIANG Fangfang1,2※, ZHANG Xiuhua3
(1.071001; 2.071001; 3.071001)
It is important to judge the density of pear flower accurately for automatic thinning. In order to judge the density of pear flowers precisely and achieve the purpose of automatic flower thinning, a density classification of pear flower images method based on improved density peak clustering algorithm was proposed in this study. The pear flower image samples used in the experiment were taken from the research base of Hebei Agricultural University, Niugang Village, Yi County, Baoding City, Hebei Province, and the variety was three-year-old Qiuyue. In this study, the images of pear flowers in natural environment were collected on April 18, 2021, when the pear flowers were in full bloom. The pear flower recognition images with high detection accuracy were obtained by using the depth learning model to detect the pear flower. The central coordinates of the target detection frame were extracted from the recognition images to obtain the data points that needed to be clustered. Secondly, in order to achieve the density classification of pear flower images, the method of selecting the cluster center was improved according to the shortcomings of the original density peak clustering algorithm in the density classification of pear flower and the requirements of pear flower density classification. The decision graph was divided into four parts by four groups of local density and center offset distance segmentation thresholds to select the cluster centers. These four parts corresponded to four grades of high, medium and low density and no thinning treatment. The accurate classification of pear flower images with reasonable density was realized. Finally, to solve the problem of inaccurate clustering classification of pear flower distribution with only cluster distribution, sparse distribution and large-scale close-up, the calculation method ofdparameter of distance between two points was improved. The pear flower scale and density grading standard were unified, and reasonable density grading could be achieved for all distribution types of pear flower images. The experimental results showed that the proposed algorithm could adapt to pear flower images of different scales. The accuracy of scale prediction was 94.89%, and the accuracy of density classification was 94.29%. Compared with the existing methods, the proposed method could achieve the density classification of local flower clusters in natural environment. the algorithm in this paper was compared with K-means algorithm and DBSCAN algorithm, and the accuracy of density classification was 94.29% and 68.57% respectively. Although the density classification accuracy of K-Means clustering algorithm was high, it lacked the algorithm steps to automatically select the clustering centers of different density classification, and was too sensitive to noise points. The density calculation method of DBSCAN algorithm lacked continuity, and the division of density grade was not precise enough. Based on the comprehensive analysis of density classification accuracy and cluster center selection method, the improved density peak clustering algorithm in this paper had the best effect. The clustering centers of different density grade could be automatically selected and the error of random initialization of clustering centers could be reduced. The proposed algorithm was robust to noise points and could eliminate noise points effectively. The proposed algorithm adopted soft statistics method for density calculation, which had continuity and was more accurate for density classification. It provides technical support for analyzing the density of pear flower and machine intelligent flower thinning.
image recognition; agriculture; clustering algorithm; density classification; position coordinates; threshold; pear flower
10.11975/j.issn.1002-6819.202207204
TP391
A
1002-6819(2023)-01-0126-10
周桂红,孙乐琳,梁芳芳,等. 基于改进密度峰值聚类算法的梨花密度分级[J]. 农业工程学报,2023,39(1):126-135.doi:10.11975/j.issn.1002-6819.202207204 http://www.tcsae.org
ZHOU Guihong, SUN Lelin, LIANG Fangfang, et al. Pear flower density classification based on improved density peak clustering algorithm[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2023, 39(1): 126-135. (in Chinese with English abstract) doi:10.11975/j.issn.1002-6819.202207204 http://www.tcsae.org
2022-07-21
2022-12-07
国家自然科学基金(62106065);河北省现代农业产业技术体系梨创新团队现代果园装备与智能化(HBCT2021210206)
周桂红,博士,教授,研究方向为人工智能、图像处理。Email:hebau_zgh@163.com
梁芳芳,博士,副教授,研究方向为人工智能、图像处理、计算机视觉、模式识别等。Email:liangfangfang@hebau.edu.cn

