湍流效应对空化流场及密封性能的影响*

梁彦兵 李香 郑国运 李 鲲 吴兆山 姚黎明 丁雪兴

（1. 合肥通用机械研究院有限公司 安徽合肥 230031； 2. 兰州理工大学石油化工学院 甘肃兰州 730050）

机械密封作为轴端旋转机械的主要密封元件， 其具有密封性能可靠、 安装操作简单及服役寿命长等优点， 被广泛应用于压缩机、 发动机和泵等旋转流体机械中[1-3］。 但是随着我国工业朝着集成化、 轻量化、零污染以及高转速的方向发展， 机械密封在高转速工况下运行时其流体的流动状态一般为湍流， 这就使得以往的层流计算模型不再适用[4-6］。 因此对湍流效应展开深入的研究， 为高速泵在工程应用中提供一定的理论指导显得尤为重要。

湍流效应的研究工作始于滑动轴承， 并受到了广泛的关注。 20 世纪60 年代， CONSTANTINESCU[7-10］开启了湍流效应研究的大门， 并基于混合长度理论，分析了湍流效应对轴承润滑特性的影响， 提出用平均速度梯度来表征湍流应力变化的一种新的湍流模型。NG、 PAN[11-12］、 ELROD 和NG[13］在上述研究的基础上， 通过引入Reichardt 经验壁面律表达式， 研究了一种可同时用于剪切流和压差流的新湍流模型， 为滑动轴承的润滑特性分析提供了理论指导。 HIRS[14］基于整体流理论提出了一种适用于较小雷诺数下的“Bulk flow” 湍流模型， 由于该模型只适用于雷诺数较低的工况， 因此存在一定的理论缺陷。 综合考虑上述3 种湍流模型， 可以发现ELROD 和NG[13］提出的湍流计算模型得出的计算结果更加准确， 这为以后人们对湍流模型的研究提供了更好的理论指导。BRUNETIÈRE[15］在ELROD 和NG[13］的研究基础上对湍流模型做了更深层次的研究并进行了模型修正， 提出了适用于较高雷诺数工况下的湍流计算模型。YASUNA和HUGHES[16］通过对层流和湍流2 种不同流态下的流体薄膜轴向动力学的研究， 得到了层流和湍流模型下的稳态平衡扰动特征响应。 BRUNETIÈRE等[17］研究了端面液膜密封在不同流动状态下的密封特性， 考虑了密封过程中Couette 流和Poiseuille 流对流体流动状态的影响， 首次使用流动因子对流动状态进行了明确的界定。 随后BRUNETIÈRE 和TOURNERIE[18］在考虑惯性效应的情况下， 对不可压缩流体中的能量方程采用平均惯性法进行处理， 最后采用有限单元法对端面液膜在3 种不同流态下的流动特性进行了分析计算。

国内张新敏等[19］和刘珂等人[20］分别基于Ng-Pan和Hirs 理论， 提出了基于湍流润滑理论分析的工程计算方法和适用于压力流与速度流共存的新的湍流计算模型。 张运清和张直明[21］也提出了一种新的复合型湍流模型计算方法， 但由于该模型计算量较大， 从而限制了其在实际工程中的应用。 近几年， 张肖寒等[22］在BRUNETIÈRE 等[17-18］提出的修正湍流模型的基础上， 对端面螺旋槽液膜密封在高转速工况及不同流态下的密封性能进行了分析计算， 最后指出了层流和湍流模型下螺旋槽几何参数和操作参数对密封性能的影响规律。 沈伟[23］引入了一种可用于表征型槽的超椭圆曲线， 分析了不同介质压力和速度条件下实际气体效应、 惯性效应和湍流效应对液膜刚度和泄漏率的影响规律， 揭示了3 种效应对稳态性能的单独影响及交互影响机制， 并对新提出的槽型几何参数进行了优化。 严如奇等[24］基于Ng-Pan 提出的湍流系数表达式， 建立了考虑湍流效应与离心惯性力效应的可压缩流体能量方程， 然后联立雷诺方程分析了不同流态下不同工况参数和平均膜厚对密封性能的影响， 得出了湍流效应对超临界二氧化碳干气密封性能的影响规律， 并提出流场计算时不可忽略湍流效应的影响。 然而到目前为止， 同时考虑空化效应和湍流效应对端面螺旋槽液膜密封性能影响的研究还不够完善。

为探究湍流效应对轴端机械密封性能及空化流场的影响规律， 本文作者以典型螺旋槽液膜密封为研究对象， 基于专业流场分析软件中的k-ω湍流模型，通过对不同转速、 进口压力、 槽深以及膜厚下的流场进行模拟， 分析湍流效应对液膜密封性能及空化效应的影响规律， 为高速泵用轴端机械密封在湍流效应下的研究奠定了一定的理论基础。

1 液膜仿真模型

1.1 几何模型

端面螺旋槽液膜密封二维平面结构示意图如图1所示。 其中ro为端面外半径，rg为螺旋槽槽根半径，ri为端面内半径，α为螺旋角，h为液膜厚度，hg为螺旋槽槽深，ω为旋转轴转速， 各槽之间的区域为密封堰区，ro与rg之间的区域为密封坝区。 密封系统在运行过程中由于端面沟槽的存在， 在槽根部附近会形成较强的动压效应， 使得密封端面分离， 并在动静环之间形成一层厚度为h的流体薄膜， 使密封系统处于非接触运行状态， 减小动静环运行过程中的摩擦磨损。

图1 螺旋槽液膜密封端面结构Fig.1 Structure of spiral groove liquid film seal

动环密封面槽型采用经典螺旋槽槽型， 其几何参数满足柱坐标系下的对数螺旋线方程：

式中：θ为展开角度， rad；r为端面液膜任意一点的半径， mm。

1.2 流场的基本假设

根据流体力学的基本理论， 考虑湍流效应下端面螺旋槽液膜密封工况参数的影响， 对液膜流场进行分析计算时， 做出如下假设[25］：

（1） 密封流体为牛顿流体；

（2） 流体薄膜与动静环两端面之间不发生流体滑移；

（3） 不考虑端面粗糙度和能量交换的影响；

（4） 忽略系统振动和动静环变形对密封性能的影响。

1.3 计算模型

1.3.1 流体力学中的控制方程

由于Mixture 模型稳定性较好， 且可适用于相互混掺的流体， 因此文中在模拟空化过程中选用Mixture 多相流模型， 其控制方程[26］如下：

式中：ρm为混合相的密度， kg／m3；vm为介质平均速度， m／s。

1.3.2 空化控制方程

Schnerr-Sauer 空化模型对空化效应描述较为准确， 且其收敛性及计算速度较快， 因此在模拟计算过程中选用Schnerr-Sauer 空化模型， 其基本控制方程[27］如下：

式中：Re为空化蒸发相；Rc为空化冷凝相； m 为相数； v 为气相； l 为液相；φ为气相体积分数。

1.3.3 流体流态判别

在端面螺旋槽液膜密封的研究过程中， 首先要进行流体流动状态的判断。 流体的流动状态主要通过流动因子ζ来判断， 如图2 和3 所示分别为旋转流速度场分布和流动因子判定模型， 当ζ＜9／16 时， 流体的流动状态为层流流动； 当9／16＜ζ＜1 时， 流体的流动状态为过渡流； 当ζ＞1 时， 流体的流动状态为湍流流动。

图2 旋转流速度场分布Fig.2 Distribution of swirling flow velocity field

图3 流动因子判定模型Fig.3 Flow factor judgment model

湍流流态的判别计算公式[17］为

式中：ζ为流动因子为单独Couette流动时周向剪切雷诺数为单独Poseuille流动时径向压差流动雷诺数；vr为径向旋转速度，m／s；vz为周向流动速度， m／s。

1.3.4 湍流模型

由于计算过程中流体的雷诺数较低， 且考虑流体黏度对流动过程的影响。 所以文中选用k-omega （kω） 中的SST 湍流模型， 其湍动能方程及比耗散率输运方程[28］为

式中：Gk为由层流速度梯度产生的湍动能；Gω为由ω方程产生的湍动能；Tk为k的扩散率；Tω为ω的扩散率；Yk为k在湍流下产生的扩散；Yω为ω在湍流下产生的扩散；Dω为正交发散项。

1.3.5 稳态性能参数

（1） 液膜开启力

1.4 网格划分

端面非接触式机械密封由于流体动压沟槽产生的流体动压效应， 在动静环之间会产生一层微米级的流体薄膜， 由于这层流体薄膜的存在， 使得机械密封在运行过程中摩擦磨损率减小、 运行稳定性提高和抗干扰能力增强[29］。

采用专业网格划分软件对端面螺旋槽液膜进行网格划分时， 首先进行几何模型的构建， 然后对各Part及旋转边界条件定义， 其次进行网格节点数的划分，获得质量合格的结构化网格， 紧接着将结构化网格转化为非结构化网格， 最终得到质量合格且可用于流场计算的非结构化网格。 在网格划分过程中主要存在以下3 个方面的划分难点： （1） 液膜整体形状呈现似镰刀形， 轴向和纵向跨尺度较大， 在划分过程中难以用同一数量级标准进行划分， 划分过程较繁琐； （2）当螺旋角过小时， 端面液膜呈现狭长状， 划分难度大， 网格质量难以达到要求， 甚至有负体积网格出现； （3） 在划分过程中需要对Block 进行多次剖分，并进行映射， 过程繁琐难度较大。

1.5 边界条件与求解器设定

密封液膜计算参数如表1 所示。 采用网格划分软件对单周期螺旋槽液膜模型进行网格划分， 划分网格时分别进行周期性边界条件和各Part 的定义。 如图4所示为单周期液膜模型和液膜的周期性边界条件设定， 将端面螺旋槽模型放大1 000 倍， 以便于观察空化效应的形成机制。 Top surface 为螺旋槽旋转壁面，Bottom surface 为静壁面， Pressure-inlet 为压力入口边界， Pressure-outlet 为压力出口边界。 将网格导入专业流场计算软件中， 选择混合计算模型（Mixture）、Schnerr-Sauer 空化模型、k-ω湍流模型， 计算过程中采用SIMPLEC 算法并用有限体积法对扩散项进行离散， 其迭代精度设为1×10-6[30］。

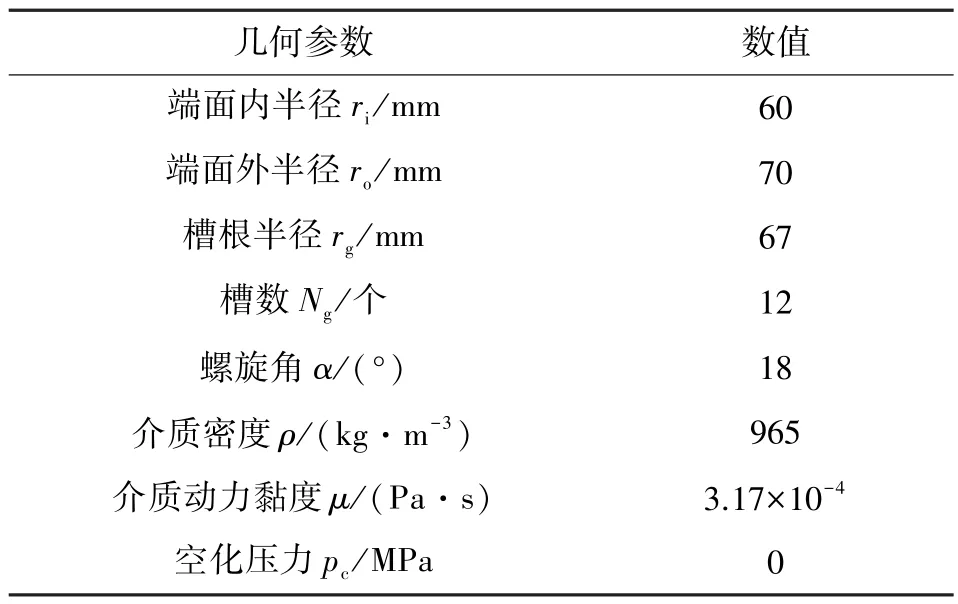
表1 螺旋槽液膜密封几何参数Table 1 Geometric parameters of spiral groove liquid film seal

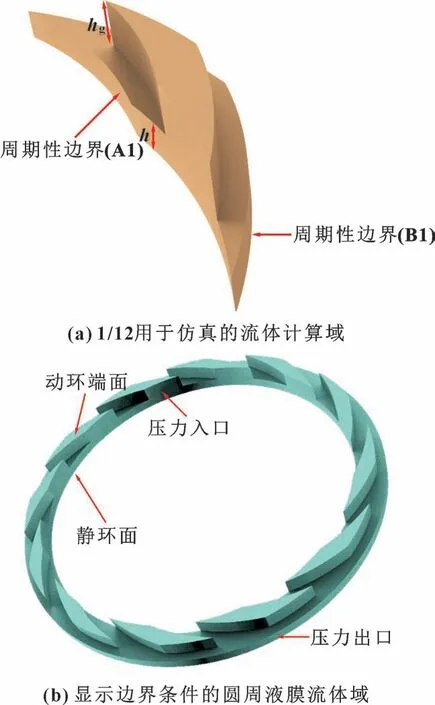
图4 轴向放大1 000 倍的液膜周期性边界Fig.4 Periodic boundary of liquid film with axial magnification of 1 000 times： （a） 1／12 of fluid computing domain for simulation； （b） the fluid domain of a circular liquid film showing boundary conditions

1.6 网格无关性验证

网格数量分别选取135 010、 156 125、 165 096、185 203 和201 131， 计算域网格加密区域为压力入口、 压力出口和槽根附近。 网格无关性验证结果如图5 所示。 可以看出， 网格数从165 096 变化到201 131时液膜的开启力和泄漏率均未发生明显的改变。 为了更加准确地获取空化细节、 提高计算精度加快收敛速度， 文中选取的网格数量为185 203。

图5 网格无关性验证Fig.5 Grid independence verification

2 结果与分析

2.1 流场模拟有效性验证

为验证模拟结果的正确性， 选择湍流经典文献[22］进行流场算例验证。 文献中选用80 K 下的液氧为密封介质， 采用数值计算的方法对湍流模型和层流模型下的密封性能参数进行对比分析。 图6 所示为选用k-ω模型模拟得到的开启力与文献值的对比。 可知， 通过模拟得出的湍流模型下的开启力与文献数据吻合较好， 变化规律基本一致。

图6 文中模拟结果与文献比较Fig.6 Comparison between the results in this paper and those in the literature

2.2 不同流态下流场分布

图7 所示为转速n＝25 000 r／min、 进口压力pi＝1 MPa、 膜厚h＝4 μm 以及槽深hg＝8 μm 时层流和湍流模型下的端面螺旋槽液膜密封压力分布及密度比分布。 可知， 两模型下的最大压力分布位置和空化区域分布位置基本相同， 层流和湍流模型下在螺旋槽的槽根处均出现了高压区， 在螺旋槽的外径侧出现了液膜空化区。 两模型计算结果的不同之处在于湍流模型下的压力最大值大于层流模型下的压力最大值， 湍流模型下的空化区域大于层流模型下的空化区域。 由此可见， 在湍流模型下由于流体黏度变大， 所以湍流模型下的空化区域大于层流模型下的空化区域。 由如图7 （a）所示的压力分布可知， 层流模型下忽略了液膜的湍流效应， 使得液膜层流模型下的承载力小于湍流模型下的值。 因此在进行机械密封的设计计算时不可忽略湍流效应对密封性能的影响。

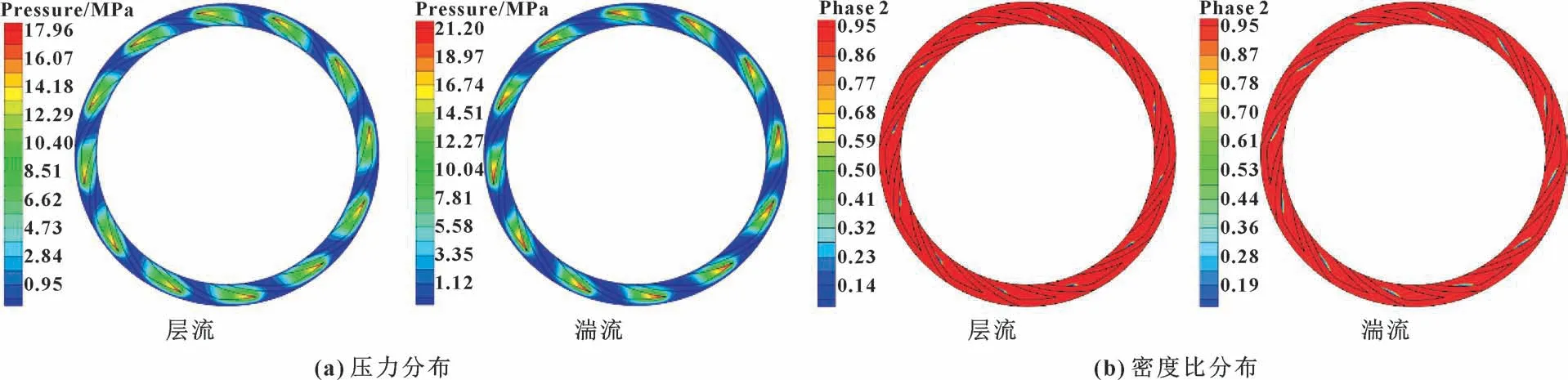
图7 层流和湍流下液膜压力分布和密度比分布Fig.7 Liquid film pressure distribution （a） and density ratio distribution （b） under laminar flow and turbulence

2.3 稳态特性分析

2.3.1 开启力

从图7 所示的端面螺旋槽液膜密封的流场分布可以看出， 湍流效应对流场的压力分布以及空化区域分布均存在一定的影响。 因此， 采用控制单一变量法取转速n＝25 000 r／min、 进口压力pi＝1 MPa、 膜厚h＝4 μm以及槽深hg＝8 μm 为基础参数研究端面液膜开启力的变化规律， 采用与前述流场分析相同的方式对开启力进行计算， 结果如图8 所示。

不同转速对湍流和层流效应下液膜开启力的影响如图8 （a） 所示。 随着转速的不断增加， 湍流模型和层流模型下液膜开启力均呈近似线性增加。 且层流模型下的开启力小于湍流模型下的值。 在转速小于10 000 r／min 时， 密封液膜呈现层流流动状态， 所以采用湍流模型和层流模型计算得到的开启力值基本一致。 当转速大于10 000 r／min 时， 流体的流动状态逐渐由层流向湍流过渡， 且随着转速的不断增加层流和湍流的差别越来越明显， 最终使得湍流模型下的开启力远远大于层流模型下的值。 随着转速的不断增加，这种趋势会越来越明显， 流体的流动也将一直保持湍流模型。

不同进口压力对湍流和层流效应下液膜开启力的影响如图8 （b） 所示。 随着进口压力的不断增加，两模型下的液膜开启力均呈现线性增加的趋势， 且增长趋势基本一致， 没有出现较大的差异。 因此进口压力对层流模型和湍流模型下的开启力没有显著的影响， 整体趋势呈线性变化。

不同槽深对湍流和层流效应下液膜开启力的影响如图8 （c） 所示。 随着螺旋槽槽深的不断增大， 液膜开启力呈现出先增大后减小的变化趋势。 与层流模型下的开启力相比， 湍流模型下的开启力值均大于层流模型， 且随着槽深的不断增加二者的差别越来越明显。 在小槽深下， 螺旋槽液膜密封的湍流效应较弱，导致开启力大于层流下的值； 当槽深较大时， 液膜的湍流效应变大， 二者的开启力差距增大。 在层流模型下， 当槽深大于12 μm 时， 螺旋槽液膜密封的开启力开始减小， 且减小速率缓慢； 在湍流模型下， 当槽深大于12 μm 时， 螺旋槽液膜密封的开启力也开始出现下降的趋势， 且其下降速率和层流变化趋势相近。

不同膜厚对湍流和层流下液膜开启力的影响如图8 （d） 所示。 当膜厚小于4 μm 时， 随着膜厚增大开启力骤降， 当膜厚大于4 μm 时随着膜厚不断增大其下降速率开始减慢。 总体来说， 考虑湍流效应的开启力值始终大于层流， 但是随着膜厚增加， 二者之间的差距逐渐减小， 其主要原因是因为随着膜厚的增加液膜的动压效应先急剧减小然后变化缓慢， 最终呈现出图中所示的变化规律。

2.3.2 泄漏率

端面螺旋槽液膜密封稳态性能参数除了开启力之外还有泄漏率， 从上述分析可以看出， 湍流效应对开启力会产生一定的影响， 由此推测其对泄漏率也会产生较大的影响。 因此在保证其他参数不变的条件下， 采用控制单一变量法取转速n＝25 000 r／min、 进口压力pi＝1 MPa、 膜厚h＝4 μm 以及槽深hg＝8 μm 为基础参数研究泄漏率的变化规律， 结果如图9 所示。

图9 不同参数下湍流和层流效应对泄漏率的影响Fig.9 Effect of turbulence and laminar flow effect on leakage under different parameters： （a） effect of rotating speed on leakage； （b） effect of inlet pressure on leakage； （c） effect of groove depth on leakage； （d） effect of film thickness on leakage

不同转速对湍流和层流效应下密封泄漏率的影响如图9 （a） 所示。 在层流模型下， 随着转速的增加，密封泄漏率逐渐增大； 在湍流模型下， 密封的泄漏率随着转速的增大变化较大， 其变化趋势明显大于层流。 另外从总体来看， 湍流模型下的泄漏率均大于层流模型下的值， 且当转速大于15 000 r／min 时， 湍流模型下的泄漏率与层流模型下的泄漏率出现了明显的差异。

不同进口压力对湍流和层流效应下密封泄漏率的影响如图9 （b） 所示。 进口压力对泄漏率的影响和对开启力的影响趋势基本相似， 2 种流态下的泄漏率均随进口压力的增加而变大， 且其增长趋势基本一致。 总体而言， 湍流模型下的泄漏率均大于层流模型下的值。 当密封介质的压力变大时， 密封环内径与外径之间的压差也会变大， 导致沿着密封泄漏方向的压力梯度变大， 最终加剧密封的泄漏。

不同槽深对湍流和层流效应下密封泄漏率的影响如图9 （c） 所示。 在层流模型下， 随着槽深的增加，泄漏率先缓慢上升后逐渐下降； 湍流模型下， 泄漏率的变化趋势与层流模型基本一致， 只是变化速率有略微差异。 总体来说， 层流模型下当槽深大于10 μm时， 泄漏率由逐渐增大变成缓慢下降； 湍流模型下当槽深大于12 μm 时， 泄漏率也由逐渐增大变成缓慢下降。 在小槽深下2 种流态的泄漏率差距小， 在大槽深下（如槽深大于14 μm）， 2 种流态下的密封泄漏率差距较大。 另外在小槽深下（如槽深小于6 μm）层流模型下的泄漏率大于湍流模型下， 在大槽深下则相反。 这是因为在小槽深时， 湍流效应不占主导地位， 泄漏率主要由层流效应决定； 当槽深较大时， 湍流逐渐占据主导地位， 其湍流剪切应力也更大， 最终导致在较大膜厚下， 湍流的泄漏率大于层流。

不同膜厚对湍流和层流效应下密封泄漏率的影响如图9 （d） 所示。 不考虑湍流效应时， 随着膜厚的增加， 泄漏率不断变大； 考虑湍流效应时， 随着膜厚的增加， 泄漏率先增大后减小。 且在膜厚大于4 μm时， 不考虑湍流效应的泄漏率大于湍流效应下的值。主要是因为在小膜厚下， 螺旋槽液膜密封的流体动压效应较强， 密封环内外径之间导致泄漏的压差较大；而膜厚较大时， 湍流效应使得密封介质黏度增大最终导致密封介质的泄漏困难。 在层流模型下， 随着端面间隙的增大， 密封介质就会沿着密封副端面进行泄漏。

2.3.3 空化面积比

端面螺旋槽液膜密封的空化现象普遍存在， 其影响因素也比较多。 从前述分析可以看出， 湍流效应对开启力和泄漏率均有较大的影响。 因此在进行分析计算时文中考虑了湍流效应对空化面积比的影响规律，在保证其他参数不变的前提下， 采用控制单一变量法取转速n＝25 000 r／min、 进口压力pi＝1 MPa、 膜厚h＝4 μm 以及槽深hg＝8 μm 为基础参数研究端面液膜空化面积比的变化规律， 结果如图10 所示。

图10 不同参数下湍流和层流效应对空化面积比的影响Fig.10 Effect of turbulence and laminar flow effect on cavitation area ratio under different parameters： （a） effect of rotating speed on cavitation area ratio； （b） effect of inlet pressure on cavitation area ratio； （c） effect of groove depth on cavitation area ratio； （d） effect of film thickness on cavitation area ratio

不同转速对湍流和层流效应下空化面积比的影响如图10 （a） 所示。 两模型下， 随着转速的增大， 空化面积比均呈近似线性趋势增长， 且其值变化较快。总体而言， 湍流模型下的空化面积比大于层流模型下的值， 且在低转速下， 空化面积区域均不明显， 密封流体只是有轻微空化； 在转速大于15 000 r／min 时，空化区域明显增加， 出现了明显的空化现象。 这与之前的研究结果相吻合， 即高转速可以促进空化效应的发生， 但是湍流模型对空化效应的影响更加明显。

不同进口压力对湍流和层流效应下空化面积比的影响如图10 （b） 所示。 两模型下， 随着进口压力的增大， 空化面积比均急剧下降。 但是当密封压力大于1.4 MPa 后， 随着进口压力的增大， 湍流模型下的空化面积比与层流模型下的值相差越来越小； 而进口压力小于1.4 MPa 时， 两模型下的空化面积比相差较大。 其主要原因是随着进口压力的不断增加， 湍流效应的影响越来越弱。

不同槽深对湍流和层流效应下空化面积比的影响如图10 （c） 所示。 两模型下， 随着槽深的变化， 空化面积比均线性降低。 但是在湍流模型下， 其空化面积比的值一直大于层流效应下的值。 因此， 湍流效应可以增加空化区域的形成。

不同膜厚对湍流和层流效应下空化面积比的影响如图10 （d） 所示。 两模型下， 随着膜厚的增大， 空化面积比均出现了逐渐下降的趋势。 但是在小膜厚下湍流效应的空化面积比大于层流下的值； 在较大膜厚下两模型下的空化面积比相差不大。 由此可知， 膜厚越大空化面积比越小， 且较大膜厚对湍流效应的影响没有小膜厚明显。

3 结论

（1） 不同转速、 进口压力、 槽深以及膜厚下，不同流态的开启力变化趋势一致， 且湍流的值大于层流。 随着转速和进口压力的增大开启力也增大； 随着槽深的增大， 开启力先增大后减小； 但随着膜厚的增加， 开启力逐渐下降。

（2） 不同转速、 进口压力以及槽深下， 不同流态下的泄漏率变化趋势相似， 而在不同膜厚下， 开启力表现出不同的变化规律， 但总体来说， 湍流下的泄漏率始终大于层流下的值， 泄漏率随着转速、 进口压力和槽深的增大而增加； 考虑湍流效应后的泄漏率随膜厚的增大先增大后减小， 与层流表现出截然不同的趋势。

（3） 不同流态下空化面积比随着进口压力、 槽深以及膜厚的增加而减小， 且变化趋势相似； 转速不同时， 2 种流态下空化面积比的变化规律一致， 均随着转速的增大而增加， 且湍流模型下的空化面积比始终大于层流模型下的值。