让学生在结构化的联系中练习和梳理——『用连乘、连除解决问题』复习课教学

执教|徐爱琴 评析|朱希萍

“用连乘、连除解决问题”是人教版三年级下册的一节复习课。这节课是在学生学习了连乘、连除解决问题的基础上进行的，学生已经会分别用连乘、连除进行问题解决。

本节复习课通过设计有结构的题组练习，引发学生对连乘问题改编成连除问题，让学生在结构化的联系中练习和梳理，感悟用连乘、连除解决的题目结构及解决此类问题的方法，沟通连乘与连除问题之间的关系，链接一步计算的问题与两步计算的问题之间的关系，从而提高学生解决问题的能力。

一、梳理用连乘解决问题的结构特征

投影出示下面三个问题：

1.超市卖出5 箱矿泉水，每箱24瓶，每瓶2 元。一共卖了多少元钱？

2.跑道每圈长400 米，小红每天跑2 圈。她一星期（7 天）跑多少米？

3.下图用小方块拼摆的立体图，一共用了几个小方块？

同时提出以下练习要求：

请你列出综合算式解答，解答后再想一想这三道题的解答有什么共同的地方？

（学生独立解答后，教师组织集体交流）

师：谁先来说一说第1 题是怎样计算的？

生1：我的计算方法是5×24×2=240（元）。

师：谁还有不同的列式方法？

生2：我的计算方法是2×24×5=240（元）。

师：这两个算式的方法有什么不同呢？

生：第一种方法先算一共有多少瓶，再算一共多少元；第二种方法是先算一箱要几元，再求5 箱一共要几元。

师：谁来说一说第2 题是怎样计算的？

生1：第2 题我的计算方法是400×2×7=5600（米）。

生2：我的计算方法是2×7×400=5600（米）。

师：这两个计算方法的想法又是怎样的呢？

生：第一种方法是先计算一天跑多少米，再求7 天跑多少米；而第二种方法是先计算7 天跑了几圈，再求一共跑几米。

师：那第3 题你们也有不同的算式吗？

生：可以用4×5×3=60（个），也可以用3×4×5=60（个），还可以用5×3×4=60（个）。

师：你们能分别说一说每个算式的第一步计算的是大立体图形的哪一个面吗？谁来针对投影的图指出你说的意思？

生1：算式“4×5×3”的第一步是计算这个大立方体前面的一个面用了多少个小方块。

生2：算式“3×4×5”的第一步是计算这个大立方体右面的一个面用了多少个小方块。

生3：算式“5×3×4”的第一步是计算这个大立方体的一层用了多少个小方块。

师：那这三道题所用的计算方法都有什么共同的地方呢？

生：它们都用了连乘的方法。

师：连乘的方法也可以说成先算什么？再算什么？

生：先算几个几是多少，再算几个几是多少。

师：计算时先要搞清楚每一步计算的几个几表示实际的什么意思。

【评析：三道连乘问题涉及到“单价、数量和总价”“速度、时间和路程”以及几何图形等方面的应用。学生通过对三道题的独立思考和解答，自然会领悟到这三道题的共同结构特征和解题方法。再通过教师引导学生进一步的质疑交流，在交流中教师有意识地让学生汇报出不同的计算方法并进行说理。这样，除了进一步认识题型的结构特征，还更加清晰地认识到连乘问题的解题关键，即每一步计算的“几个几”是表示计算了实际问题的什么意思，渗透了乘法中的运算定律。】

二、梳理用连除解决问题的结构特征

1.改编连乘问题为连除问题

师：这三题解决了，我们把问题变成已知条件，把其中一个条件变成问题，你会改编吗？同桌之间相互交流一下。

【评析：这里让学生将刚才的三道题的问题作条件，其中的一个条件当问题。三道连乘问题就变成了九道用连除解决的问题。这样一改编，学生就明白连乘连除结构的可逆关系，为下一环节寻找连乘、连除问题之间的关系积累了活动经验。】

2.梳理连除问题的结构特征和解题方法

师：同学们刚才编出了九道题，我们从中选择三道来解决。出示如下三题：

（1）超市卖出5 箱矿泉水共240 元，每箱24 瓶，每瓶多少元？

（2）小红一星期（7 天）共跑了5600 米，她每天跑2 圈，跑道每圈长多少米？

（3）用60 个小正方体摆成一个大长方体，每层摆3 行，每行摆5 个，可以摆几层？

请你列出综合算式解答，解答后再想一想这三道题的解答有什么共同的地方。

（学生独立解答后，教师组织集体交流）

师：谁来说一说这三道题是怎样解答的？

生1：第（1）题：240÷5÷24=2（元），先求每箱多少元，再求每瓶多少元。

生2：我有不同的方法240÷（5×24）=2（元）。先求5 箱一共是多少瓶，再求每瓶多少元。

生3：第（2）题：5600÷400÷2=7（天）。先求一共跑了几圈，再求一共跑几天。

生4：第（2）题我是这样做的：5600÷（400×2）=7（天）。先求每天跑多少米，再求一共跑几天。

生5：第（3）题我有三种做法：60÷3÷5=4（层），60÷5÷3=4（层），60÷（5×3）=4（层）。

师：解答这三道题有什么共同的地方？

（学生说出都可以用连除来解决，这时教师在课题“连除”两字下面划上一横）

师：现在你能说一说为什么用连除解决吗？

生：比如第（1）题把240 元钱平均分成5 箱，用除法计算得出每箱48 元，再接着把48 平均分给24 瓶，所以还是用除法。

师：第（2）题呢？为什么还是用除法？

生：因为这一题实际上是求5600 米里面包含几个400 米，求出一共有14 圈，每2 圈一天，还是求14 里有几个2，所以还是用除法。

师：现在你们知道解决这些问题为什么用连除吗？

生：这些问题都是在不断地分，有的是平均分，有的是求包含几个几。

（教师随机板书“先分再分”）

师：另一种方法为什么要先乘再除呢？

生：这种方法是先求几个几再分。

【评析：这一环节的功能除了让学生理清用连除解决的问题结构及解题方法，还让学生探究了用连除解决的问题原理，都是先分再分。从而明白为什么用连除解决或者先乘再除解决的道理。】

三、梳理连乘问题和连除问题的联系

师：回顾一下，这两类问题有什么相同和不同之处？解答这类问题的关键是什么？

生1：都要认真审题，弄明白告诉了什么，要我们求什么。

生2：关键弄明白先求什么，再求什么。

生3：连乘与连除问题有一种“相反关系”。

生4：连乘是先求几个几，再求几个几，累加起来的；连除是先分再分，是不断分下去的。因此刚好相反。

【评析：这一环节目的就是沟通连乘连除问题之间的联系。学生有刚才改编的经历，再加上通过问题情境、解题算式及方法算理的比较，发现连除与连乘是互逆关系的运算方法。第二个目的是在变中发现不变。解决两类问题都需要认真审题、选取有用的信息，搞明白先求什么，再求什么，让方法落到实处。】

四、在练习有联系的题组中提升解决问题能力

1.在连一连中横向巩固题型结构

①张大伯摘的橘子装了2 车，每车10 筐，每筐50 千克，一共摘了多少千克橘子？

②张大伯摘了10 筐橘子，每筐50 千克，每千克卖2 元，一共可以卖多少元？

③张大伯摘的橘子装了2 车，每车10 筐，还剩下50 筐，一共摘了多少筐橘子？

A.2×（10×50） B.2×10×50 C.2×10+50

①张大伯共摘了1000 千克橘子，每筐50 千克，10 筐装一车，可以装多少车？

②张大伯卖了10 筐橘子，每筐50 千克，一共卖了1000 元，每千克卖多少元？

③张大伯共摘了1000 千克橘子，每筐50 千克，卖出10 筐，还剩多少筐？

A.1000÷50÷10 B.1000÷（50×10） C.1000÷50－10

（1）学生独立完成，核对答案

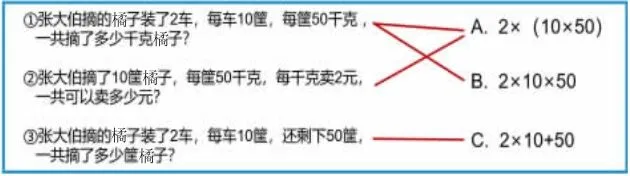
（2）分析错题

师：上面这组题目哪一题容易错？

生1：第①题，只连了一个算式，没考虑多种方法解决。

生2：第②题，我多连了一条，把它跟第②题连上了。而2×10×50是不能解决第②个问题的，因为10 筐橘子和每千克2 元这两个条件没有关联。

生3：第③题要注意了，它是用乘加来解决的。我们前面往往用连乘解答，想当然都用连乘来解答了。

师：下面这组你觉得哪题要提醒大家？

生：这组题的第②题不能连A 这个算式，1000 元不能除以每筐50 千克，因为1000 元和每筐50 千克没有关联。

（3）总结收获

师：解决了这几道题，你有什么收获？

生1：做题目要仔细审题。不能今天学习了连乘连除就想当然都用连乘连除来解决。有时不一定都是这样做的。

生2：这些题目看起来都很相似，但是只要有一个信息发生变化，数量关系就会发生变化，所以我们在解决问题时要明确先求什么，再求什么。

生3：解决问题时要选择有用的信息和有关联的信息。

【评析：在这样情境相似、数据相同的题组中放置一道不能用2×10×50 来解决的问题，因为10筐橘子和每千克2 元这两个是不相关联的信息，不能解决相关问题。在这样情境相似、数据相同的连乘解决的题组中放置一个先乘后加；在连除解决的题组中放置一个先除后减。这样会让“认真审题”落到实处。】

2.在扩缩变换中纵向感受题型的演变

师：你能把两步计算的问题改成一步计算的问题吗？先自己轻轻说一说，再集体汇报。

生1：把张大伯摘了“10 筐橘子，每筐50 千克”，这两个条件合并为“每车载500 千克”。求一共摘了多少千克橘子？（如下图所示）

列式就由2×10×50→2×500，两步计算就成了一步计算。

生2：第二组中的“每框50 千克，10 筐装一车”改为“每车装500 千克”也就成一步计算了。（如下图所示）

算式也由“1000÷50÷10”变成了“1000÷500”，从两步计算缩成了一步计算。

师：两步计算我们能缩成一步计算，那么，一步计算问题怎么扩成两步、三步计算呢？

学生回答把其中的一个条件不直接告诉，例如把“10 筐装一车”改为“左边放8 筐、右边放2筐”就成了三步计算的问题。

师：通过刚才的改编你有什么发现呢？

学生各抒己见后，教师小结：两步计算的问题，将其中的两个条件合并为一个条件就成了一步计算。两步计算的问题，将其中的一个条件不直接告知扩成两个条件告知的形式就成了三步解决的问题，以此类推。

3.在补条件选问题中提升信息提取能力

师：刚才我们会扩缩变换了，现在你会根据算式补上条件和问题吗？出示下面练习。

苹果每箱有2 层，每层15个。

①2×15×20（ ）

②2×15-20（ ）

③600÷15÷2（ ）

A.一共有600 个苹果，可以装多少箱？

B.食堂买来600 箱苹果，一共有多少个？

C.食堂买来20 箱苹果，一共有多少个？

D.吃掉20 个，还剩多少个？

【评析：这一环节能让学生充分经历连乘连除应用问题解决题目结构演变形成的全过程。经历了学生就有感悟，经历了学生就有话可说，经历了学生对一步解决的问题与两步三步应用问题的结构特征就会了然于胸。】

4.在解答非良构问题的过程中提升问题解决能力

刚才我们用三条信息解决了问题，课件保留下面信息①②③，现在再给你一些信息，然后逐步增加④～⑧信息。再提出：你能选择一些信息提出问题并解决吗？请完成《学习单》。

①学校食堂买了20 箱苹果，

②每箱有2 层，

③每层有15 个，

④全校有6 个年级，

⑤每个年级有3 个班，

⑥平均每班有36 人，

⑦每4 个苹果约重1 千克，

⑧每千克苹果5 元钱。

我选信息（序号）问题算式例如①②③一共有多少个？2×15×20

【评析：问题解决的核心目标是提升学生发现问题、提出问题、分析问题和解决问题的能力。而培养学生这样的“四能”需要有特定的环境，需要给学生创设特定的素材，让学生在自主选择有用信息解决相应问题中提升，让学生在根据算式选取有用信息中提升。本环节通过在上一环节已经熟悉的三条信息中加入5 条信息。在多个信息中选取有用的信息需要学生甄别、取舍。也就在这个非良构的问题情境中，学生的问题解决能力得到了提升。】

五、全课总结（略）

【总评】

本节课我们力求体现结构化视域下的教学设计，关注元素特征中发现问题本质，关注关联中建构知识体系，关注循环中提升问题解决能力。

元素是指构成事物的最基本结构。功能是由它构成的基本结构决定的。连乘连除解决问题最基本的元素就是乘了再乘、除了再除。为什么要乘了再乘、除了再除呢？因为连乘问题解决的是先求几个几再求几个几。而连除指的是先分再分的事情，因此要先乘再乘、先除再除。这样在发现元素特征中掌握问题本质。

关联是指事物之间的联系。这里的联系有横向、纵向；有显性、隐性的关联。本节课让学生通过有效的题组练习后发现连乘、连除解决问题的可逆联系。通过一步到两步到三步的扩缩变换中发现题目结构的凝聚与演变，建构了知识体系。

循环是数学教学必须遵循的原则。因为数学知识是一个不断螺旋上升的过程。这就需要我们在教学中循序渐进。本节课从单一题型的连乘解决问题→连除解决问题→乘加→除减→再到题型的扩缩→自主选择有用信息的综合应用。每一环节都围绕着提升学生问题解决这一核心素养展开教学。

总之，这节课充分体现了在结构化视域下进行有结构的练，促进学生有联系的学。