利用图示明晰“找次品”的原理
文|王燕芬
《找次品》的学习中,学生难以理解的问题是:怎样理解“保证”和“至少”?为什么要分三堆?为什么要尽可能平均分?教学中可以利用图示帮助学生更好地理解“找次品”的原理。
一、定位原理——觅“题眼”
1.出示题组
(1)有3 瓶钙片,其中一瓶少了3片(次品),你能设法把它找出来吗?
(2)9 个零件里有1 个是次品(次品重一些),假如用天平称,至少称几次就保证一定能找出次品?
2.独立学习
(1)读一读:每一题是什么意思?
(2)比一比:有什么共同点?“保证”和“至少”是什么意思?
3.全班交流
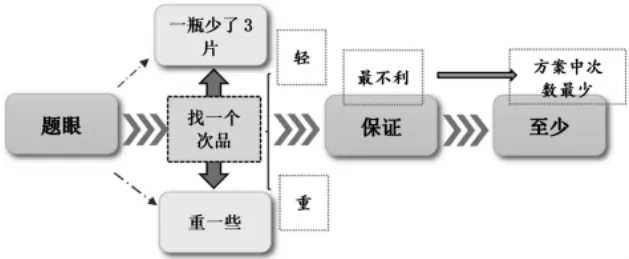
引导学生发现:(1)找次品问题是一堆物体里找一个(轻或重),而并非找几个次品;(2)“保证”一词,是指多种方案中,以“最不利”角度思考,确保找到次品;(3)“至少”一词,即是在保证一定能找出次品的方案中所用次数最少的那种方案。
二、三分原理——探“方案”
1.讨论:“8 个乒乓球里有1 个是次品(次品重一些),用天平至少称几次就一定能找出次品?”分成几堆才能保证找到次品次数最少?
2.交流汇报
(1)如果分成两堆(4,4),称一次后次品锁定在4 个中。
(2)如果分成三堆(3,3,2),称一次后次品会锁定在最多的一堆3 个中,因为数学是研究运气最差的情况。
(3)如果分成四堆(2,2,2,2),任意挑两堆称一次后,次品还是锁定在另外两堆(2,2)中,也就是锁定在4 个中。如下图所示:
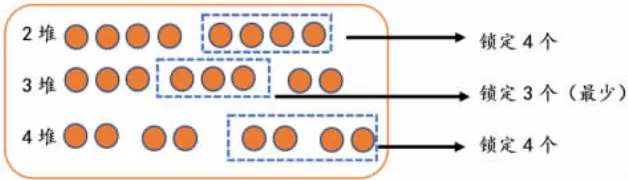
3.结合图示,发现要点:次品锁定的范围越小,找到的机会就越大
4.组内交流,例外辨析
(1)如6、10、12 等这些数分成两堆或三堆,称的次数是一样的。
(2)如8、16 等这些数分成三堆比分成两堆的方法更优化,也更具有通用性。因此,努力将物品分成三堆是有据可寻的。
三、均分原理——寻“最优”
1.思考:分成三堆,怎样分最合理?
2.结合图示,全班交流
(1)分类讨论:①如果把8 个分成(1,1,6),称一次后,最坏的情况是将次品锁定在6 个里;②如果分成(2,2,4),称一次后最坏的情况是将次品锁定在4个里;③如果是(3,3,2),称一次后最坏的情况是将次品锁定在3 个里……称一次后,要找到三堆中最大的数量作为下一次需要重新分配称量的总量。具体分析情况如下图所示:
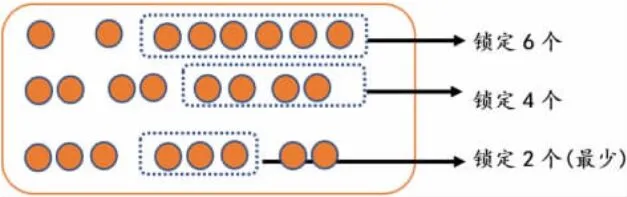
(2)发现将三个数变得相等或尽可能接近,就会使最大值降到最小。
3.寻找最优,建立模型:改变乒乓球数量,探寻最佳分法,得出结论
结合图示探究,引导学生发现“找次品”中的核心原理,有效提高学生的推理能力,实现学生思维方式的转变,从而实现真正掌握找次品原理的目标。

