基于混合遗传算法的成品油二次配送优化

孙厚举

（江苏建筑职业技术学院信电工程学院，徐州 221000）

0 引言

多周期库存路径问题［1］（inventory routing problem with multi period，IRP‑MP）属于非确定性多项式（non‑deterministic polynomial，NP）困难问题［2］的一种，是通过供应商管理库存策略（vendor managed inventory,VMI）［3］，在无限长的时间内周期性地进行一对多补货配送方案的规划和执行。成品油公路运输问题是典型的多周期库存路径问题，石油公司负责对各加油站油品库存的监控，统筹制定油品配送方案，确保配送高效且可靠。通常情况下，石油公司将制定总运距尽可能短的运送计划，以实现高质量的物流运输目标。

学术界对成品油公路运输的研究经历了从精确算法到智能化算法的过程。田立新等［4］采用0-1 规划模型解决单周期成品油运输问题。宋杰鲲等［5］采用最短路径和最小费用模型制定成品油运输模型。张立峰等［6］提出了两阶段路径规划模型，首先使用聚类算法将配送需求合并分载，然后改进遗传算法计算最终配送路线。李珍萍等［7］考虑了多种约束条件，提出了一种混合整数规划模型，继而使用遗传算法模型规划运送路线。张雄等［8］使用改进蚁群算法求解了带时间窗口的车辆路径问题。Xu 等［9］提出了多目标粒子群优化算法制定配送方案。文献［10‑11］研究了启发式算法求解多周期库存路径问题，文献［12］介绍了运输成本问题，本文在设计混合遗传算法的评估函数时参考了其中的部分因素。

1 成品油公路运输问题描述

成品油公路运输研究的是成品油运输二次配送阶段问题［13］。一次配送阶段主要是从炼油厂将成品油运送至各地级市的油库，一个省往往只有一个炼油厂，一个地级市只有一个油库且运送方式多为管道运输，几乎不需要复杂的规划模型。二次配送［14］是从油库将成品油运送至加油站，目前石油公司统一采用主动配送方式，即石油公司根据液位仪系统时时监控所有加油站多种油品的存量，根据各加油站油品的消耗情况生成配送需求，然后使用算法规划配送时间和配送量。成品油公路运输多周期规划问题中，通常每12 小时为一个周期，将全天运输计划分为早班和晚班，少数地区可能存在24小时为一个周期的情况。

问题模型与假设条件如下：

（1）允许油罐车跨地级市选取就近油库进行提油，各油库油品存量充足，不存在油品不足的情况。

（2）油库可设定当前可用油品，并可设定营业时段。

（3）每个地级市拥有大量加油站，且每个加油站都安装了液位仪，拥有近三年液位仪数据。

（4）油罐车分为汽油车和柴油车，汽油和柴油不可混装在一辆车上，不同的汽油油品不可以混装，但可以同时装在同一辆油罐车的不同隔仓里。

（5）油罐车可以分载，一辆油罐车可以一次给多个加油站配送油品。

（6）拥有油库到各加油站的距离，加油站与加油站之间的距离。如果运距不存在，则用9999公里代替。

（7）油罐车下班后停车点为油库。

（8）拥有各种约束数据，例如加油站限制拖车，限制挂车，限制配送时段等数据。

2 建立数学模型

数学符号定义如下：

P={p0,p1,…,pn}：整个规划时间段，其中元素p0和p1代表第一个规划周期的开始和结束时间，p2和p3代表第二个规划周期的开始和结束时间，以此类推。

Q={q1,q2,…,qn}：一辆油罐车的隔仓容量，其中n表示隔仓数量，qn表示第n个隔仓的容量。

K={Q1,Q2,…,Qn}：油罐车辆，其中Qn表示第n辆油罐车的隔仓容量集合。

G={g1,g2,…,gn}：油品列表，其中gn表示第n种油品的油品编号。

V={v1,v2,…,vn}：油品体积，其中vn表示第n种油品的体积。

D={(G1,V1),(G2,V2),…,(Gn,Vn) }：所有油库信息，其中(Gn,Vn)表示第n个油库的油品种类以及可用体积。

S={s1,s2,…,sn}：所有加油站。

D={(G1,V1),(G2,V2),…,(Gn,Vn) }：所有加油站的各种油品的当前体积。

SV={{S1,V1},{S2,V2},…,{Sn,Vm}}：各加油站实际配送量。

VM={v1,v2,…,vn}：加油站油品的最大容纳体积，其中vn表示第n种油品的最大可容纳体积。

SM={(G1,VM1),(G2,VM2),…,(Gn,VMn) }：所有加油站每种油品的最大可容纳体积。

T={t1,t2,…,tn}：加油站油品的预计断货时间。

O={(G1,T1),(G2,T2),…,(Gn,Tn)} ：所有加油站的所有油品的预计断货时间。

DS={ds1,1,ds1,2,…,dsi,j,…,dsn-1,n}：各运输节点间的距离，其中dsi,j表示节点i到节点j之间的距离，其中节点i和节点j可以是油库也可以是加油站或者停车场。

R={r1,r2,…,rn}：各加油站预计需求量。

v：车辆行驶速度。

SLi：油罐车在油库提油时间。

STi：加油站卸油时间。

c：断货时长惩罚。

p：不容纳体积惩罚。

根据以上描述，成品油公路运输多周期规划目标定义如下：

式（1）表示规划方案的总运输成本；式（2）表示规划方案的总断货惩罚；式（3）表示规划方案的总不容纳惩罚；式（4）表示该问题的总目标是实现所有周期中每辆油罐车的总运输成本、断货惩罚和不容纳惩罚最小。

在实际运输方案中存在如下约束：

式（5）表示限制每个加油站节点的入度和出度都必须为1；式（6）表示限制油罐车的每个隔仓满载率必须大于90%。此外还需要满足部分其他约束条件，比如加油站可容纳约束，因为油罐车的每一个隔仓在运输途中满载率要么为0，要么必须大于90%，所以隔仓卸油时必须一次卸完，不允许出现加油站油罐已满而隔仓未卸完的情况。部分城市对油罐车有交通管制，要求凌晨0点到6点通行，其他时段不允许通行。

3 混合遗传算法模型

3.1 算法编码方案

本文提出一种混合遗传算法（RMH），算法采用一位编码方式表示配送方案，但因为配送方案较为复杂，所以在编码时将每辆油罐车的配送路线进行了封装，所有油罐车的配送路线组合在一起就形成了完整的配送方案。其中，每辆油罐车的配送路线都再次被细化为三部分，即时间节点、配送路线和装载方案。时间节点包括油罐车到达油库时间、等待油库营业时长、装油时长、到达加油站时间、卸油等待时长、卸油时间，如果存在分载情况，则提供到达下一加油站时间以及卸油等待时长和卸油时间，最后加上到达下一次提油油库时间。配送路线包括油库和加油站。装载方案包括每个隔仓装载的油品种类和装载量。如图1所示，该编码表示某油罐车一次配送路线的编码。

图1 油罐车一次配送路线编码

编码中将时间节点、配送路线、装载方案、油罐车配送方案分别封装为类，则通过这些类的对象即可表示多周期配送路线方案。

3.2 算法过程

求解成品油公路运输多周期规划问题的算法流程如下。

3.3 构造初始解

首先利用松弛下界模型将部分约束条件放开，快速构造符合松弛模型的解，然后利用子回路消除方法［15］将配送方案中的子回路消除，再使用精确计算方法找到较为优秀的解放入初始解集合。假设某配送规划问题中只包含1个油库D，和16个加油站，记为{s1,s2,…,s16}，在松弛下界模型下构造的解可能并不是一条连续路径，而是多条子路径，其中多条子路径并不经过油库D。每条路径用R{si,sj,…,sn}表示，经过子回路消除操作之后，得到一条经过所有节点的回路，这条回路是开销最小的。如表1所示。

表1 子回路消除过程

其中，s2、s7、s11三个节点在构造时就没有包括在子回路中，子回路消除是通过依次计算子回路之间的距离将子回路串联在一起，形成一条回路，所以消除子回路后依然包含s2、s7、s11三个节点。通过松弛下界模型构造的规划路径R1至R5，只有R1是包含了油库的，其他规划路径都没有取油油库，经过子回路消除之后合并成为一条规划路径，然而一辆油罐车的油罐数量一般为4～5 个，也就是说，一辆油罐车到油库提一次油，最多只能配送5个加油站，如果子回路中加油站数量小于等于三个，则设定一个油库即可。所以调整后的子回路消除算法的消除过程如表2所示。

表2 改进后子回路消除过程

目标函数［16］是启发式算法中最为关键的设计，对于已经构造好的规划方案，通过目标函数进行评估，淘汰较差的解，保留优秀的解，同时配合模拟退火策略，按照一定的比例保留不够优秀的解，加强算法的全局搜索能力。

3.4 迭代搜索

合法的初始解生成之后，通过启发式算法的迭代进行局部搜索［17］，在解空间中不停地探索更优秀的解，然后用更优秀的解替换解集中较差的解，然而迭代搜索需要既保持当前解的优点，又要实现解的优化，这在实际问题中很难实现，也是设计迭代搜索的目的。首先我们认为整个问题的解空间在多维坐标系中是连续的，因此迭代时需要在解的邻域做搜索，所以邻域操作［18］是启发式算法迭代的核心操作。

本文提供了两种测量用于调整配送方案的领域操作。第一种邻域操作为简单的删除或者添加更为经济的新节点，或者删除某个节点；第二种是在不同配送路径中交换节点。第一种操作方式较为简单，可以根据目标函数直接评估，决定新增节点和删除节点。第二种操作方式不需要考虑某个节点被多次配送或者未被配送。第二种邻域操作方式的调整过程如表3所示。

表3 交换子路径节点操作过程

为防止一次邻域操作导致解在解空间中偏移过多，建议一次邻域操作只交换1～2次节点。

4 实验结果及分析

为了验证算法的有效性，本研究对3 个周期、5～50 个客户的小规模算例和6 个周期5～30 个客户的中规模算例，以及6 个周期，客户数分别为50、100、200的大规模算例进行测试。本节将对分支切割算法（branch‑and‑cut，BC）算法［19］、核启发式算法（kernel search heuristic，KSH）算法［20］和本文提出的RMH算法进行对比。

在小、中规模算例中，本文提出的RMH 算法在多数算例上取得了理论最优解。与BC 算法和KSH算法的对比结果如图2所示。

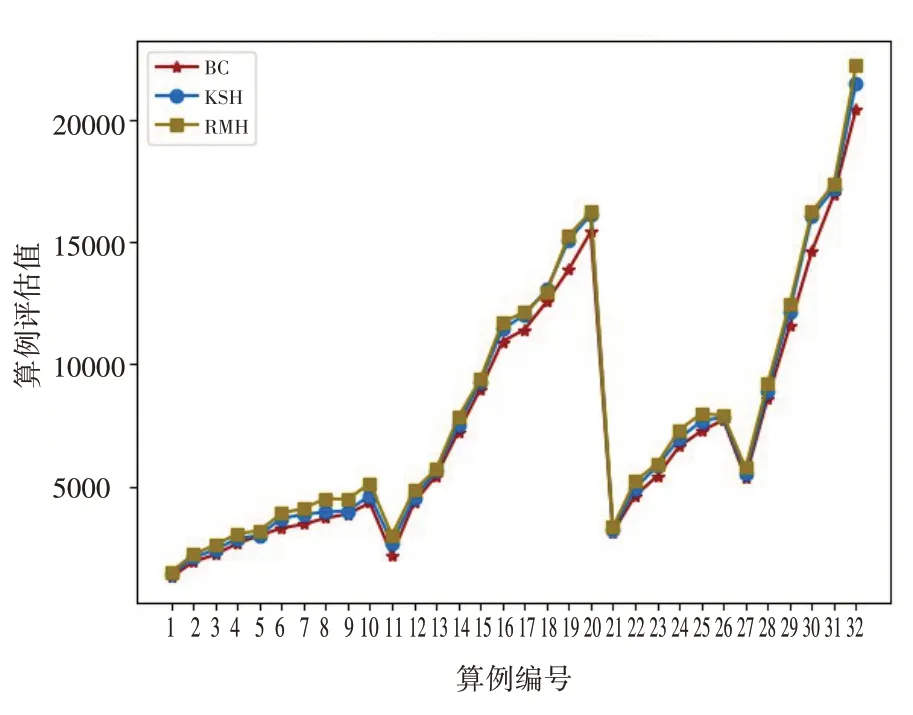
图2 小、中规模算例的对比结果

图2给出的是小、中规模算例计算结果的平均值。其中BC 算法为精确算法，在同样取得较优解的情况下，所用时间最短。从图2 不难看出，对于3周期的算例来说，三种算法得到的最优解的平均值几乎没有太大区别。中等规模算例下，KSH 算法和RMH 算法的平均值较BC 算法稍微有一些优势，但总体差别不大，但计算用时明显比BC算法要高。

对于大规模算例，周期达到6个，客户节点最多达到200 个。随着客户节点数量的增加，BC 算法的劣势越发明显。大规模算例的对比结果如图3所示。

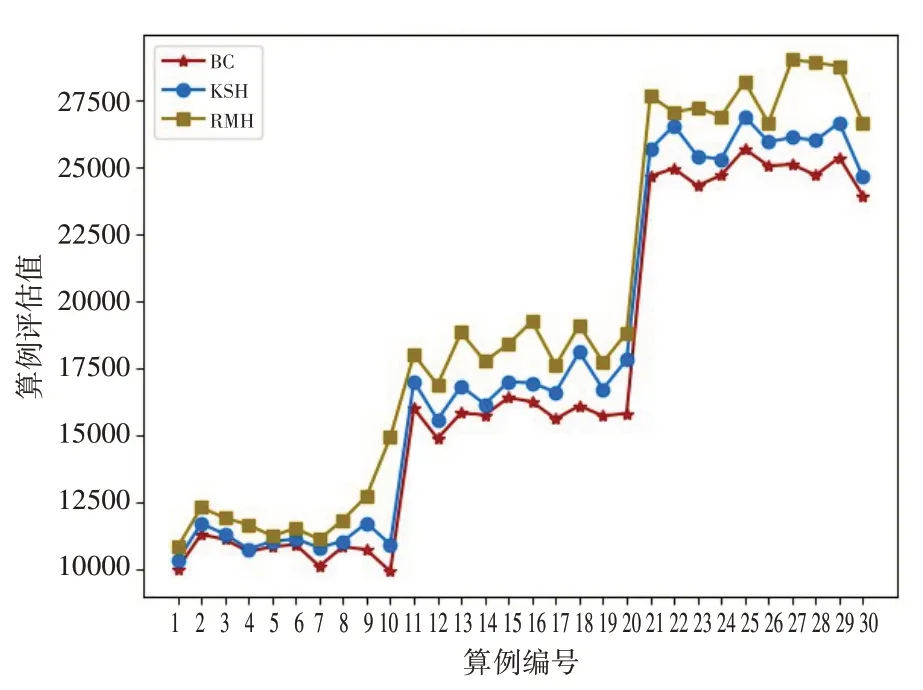
图3 大规模算例的对比结果

从大规模算例的求解结果可以看出，该研究提出的RMH 算法和KSH 算法的平均结果明显比BC 算法更优秀，而且客户节点数量越多，差距越明显，证明了精确算法在求解大规模库存路径问题上存在缺陷。而RMH 算法相比于KSH算法依旧有明显优势，总运送成本平均降低12.3%，而且平均计算时间也相对更短，通过实验对比，从求解质量和时间代价两个方面体现了RMH算法的性能和效率。

5 结语

针对成品油公路运输多周期规划问题，该研究提出一种混合遗传算法模型RMH，该模型可在多数小、中规模算例中求解到理论最优解。相较于BC 算法和KSH 算法，RMH 算法在大规模算例集获取的规划方案中优势明显。当然，该方案也存在一些不足。实际操作中，若后续需人工调整5%左右的规划路线，则会影响其它路线正常运输，牵一发而动全身，最终导致规划方案无法正常使用。因此，如何获得100%可用的规划方案是后续的重要研究工作。