岩溶地层长锚索穿越溶洞锚固力计算方法研究

肖国庆，施成华，叶承敏，孙晓贺，宋银涛，郑可跃

(中南大学 土木工程学院，湖南 长沙 410075)

随着城市发展的需要，在岩溶分布较广地区建设地铁已不可避免。由于岩溶地层具有的复杂性，对地铁建设将产生很大的困难与挑战[1]。目前车站施工常采用明挖深基坑法，在基坑工程施工过程中存在一些难以预估的风险，如：地表沉降[2-4]、基坑塌陷[5-8]等。而这些风险归根结底还是与围护结构的稳定有关，当基坑围护结构采用桩锚结构时，锚索穿过溶洞时锚固力有一定程度的降低，影响基坑施工安全。现阶段关于锚索锚固力计算理论的研究，主要有2个方向。一是假设注浆体与围岩界面间剪应力沿锚固段全长均匀分布的平均剪应力理论。LITTLEJOHN 等[9]假设黏结力沿锚固段全长均匀分布，提出了拉力型锚索锚固力设计公式。程良奎等[10]假定锚固体与周边岩土体界面的黏结强度为定值，提出了压力型锚索的设计方法。二是假设锚固力沿锚索轴线非均匀分布的非平均剪应力理论。PHILLIPS[11]认为拉力型锚索的锚固体剪应力沿锚固段呈指数分布，并由此得到了极限锚固力计算公式。LI等[12]提出了“锚固解耦段”的定义，认为部分解耦段与未解耦段面积组合的最大值即为注浆锚杆的极限锚固力。KIM[13]为得到锚固体与岩体分界面的荷载传递规律，采用t-z曲线法，取得了较好的研究效果。刘小斌等[14]通过对不同长度拉力型锚杆进行循环加载极限试验，发现锚固体轴向应力先升后降，黏结应力具单峰性，以及拉力型锚杆的锚固长度与极限抗拔承载力成正比。LIU 等[15]为研究锚杆荷载传递规律及不同锚固条件下的有效性，考虑节理张开位移，将弹性地基梁模型和锚杆拉拔模型相结合，推导出单个节理面沿锚杆应力分布的解析解。HYETT 等[16]基于剪应力与剪切位移的线性关系，分析了裂隙围岩下锚杆的轴力分布规律，适用于实际的裂隙围岩条件。周炳生等[17]基于锚固体界面剪切位移分布曲线的统一形式，推导了无限长锚体界面的位移、轴力以及剪切应力的计算公式。CHEN 等[18]分析了锚杆的系数、弹性模量和直径对锚杆荷载传递性能的影响，认为锚杆的轴向载荷从锚固端向自由端衰减，与拉拔荷载无关。刘超等[19]考虑压力型锚杆灌浆体受压产生径向膨胀的影响，推导了锚杆极限抗拔承载力与临界锚固长度的计算公式。综上所述，关于一般地层锚索锚固力的计算，国内外学者已进行了较为深入的研究，然而针对岩溶地层长锚索穿越溶洞时锚固力的计算，目前尚未有明确的计算方法，同时锚索锚固力受溶洞的影响因素也缺乏系统的认识。本文依托徐州地铁2号线淮塔东路站基坑支护工程，采用荷载传递法，基于剪切位移法非平均剪应力理论，推导锚索穿过溶洞的锚固力理论计算公式，同时对锚固力的影响因素进行系统的分析，研究结果可为工程实际提供理论指导。

1 长锚索穿越溶洞锚固作用机理

1.1 一般地层锚索锚固作用机理

锚固单元体，主要由锚固剂、锚杆(索)、锚固剂-围岩界面、锚固剂-杆体界面、围岩组合而成，简称“三体两面”结构 。如图1 所示，锚索由锚头、自由段和锚固段3部分组成。将锚固剂与锚索之间接触面称为第一界面，围岩与锚固剂接触面简称为第二界面。

图1 锚固单元体结构组成示意图Fig. 1 Schematic diagram of the structural composition of the anchoring unit body

当长锚索发挥支护作用时，锚固单元体的应力状态如图2所示，其受到的径向和轴向应力分别以σv和σr表示。

图2 锚固单元体应力分析Fig. 2 Stress analysis of anchorage unit

基于局部共同变形假设，把围岩体对锚索的剪切力简化为一系列独立作用的切向弹簧，同时锚固体微段上的应力与锚固体和围岩之间的相对位移是线性关系。对一般地层，锚索没有穿越溶洞，剪应力应处处连续，根据该假定的锚索锚固段力学计算简图如图3所示。

图3 不考虑岩溶锚固段力学计算简图Fig. 3 Mechanical calculation diagram without considering karst anchorage section

1.2 考虑岩溶锚索锚固作用机理

以全填充型溶洞为例，当锚索锚固段部分穿过溶洞时，此时锚索锚固力有一定程度的降低，计算简图应按图4 所示。此时把锚固段分成3 段分开计算，值得注意的是，在岩层与溶洞交界处，应满足变形协调条件与静力平衡条件，即剪应力会发生突变，而正应力与位移连续。

图4 考虑岩溶锚固段力学计算简图Fig. 4 Mechanical calculation of karst anchorage section

2 长锚索穿越溶洞锚固力计算方法

2.1 计算假定

考虑到实际施工时锚索打入岩层时有一定角度，将锚索锚固体划分为若干子锚固段，如图5所示，并作如下假设[21]：

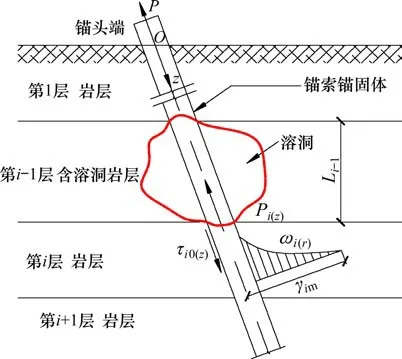
图5 子锚固段分析模型Fig. 5 Analysis model of sub-anchorage section

1) 同一子锚固段锚固体及周围岩土体均为均质弹性介质；

2) 同一子锚固段锚固体和岩土体之间力学参数为常值；

3) 锚固体横截面上正应力均匀分布，不考虑注浆体的破坏；4) 锚固体与周围岩土体间无明显的相对滑移；5) 溶洞填充物与周围岩层结合密切，与锚索锚固体也紧密接触。

2.2 锚索锚固力的推导

根据荷载传递法，将锚固体视为连续弹性体，分成若干连续弹性的单元[22]，如图6 所示，根据受力平衡，对z位置的锚固段dz有：

图6 荷载传递法计算简图Fig. 6 Calculation diagram of load transfer method

而dz段的压缩量为：

联立式(1)和(2)可得：

式中：C为锚固体的周长；z为距锚固始端距离。

设锚固体的半径为r0，弹性模量为Ep以及第i段锚固体与周围岩体剪切面上的剪切位移和剪应力分别为ui(r0)和τi(z)。由式(3)得：

基于剪切位移法原理[23]，锚固体侧岩土体剪应力与剪切位移为线性关系。锚索锚固体侧岩土体剪应力和剪切位移可表示为：

式中：ui(r)为距锚固体轴线水平距离r处的位移；Gis为周边第i段岩体的剪切模量；rim为第i段岩层中变形可以忽略不计的最大半径，一般rim=2.5li(1-μis)；li为第i段连续岩层长度；μis为第i段岩层的泊松比。

联立式(4)和式(5)可得：

式中：ki为第i段岩层的剪切刚度。

求解式(6)可得：

式中：C1和C2为待定常数；αi为与第i段岩层剪切刚度有关的常数。

根据锚索锚固体轴力Pi(z)与应力应变之间关系可得：

将式(8)代入式(10)和式(5)，可得连续锚固体的锚索轴力与剪应力的分布函数为：

式中：Ap为锚索锚固体的截面积；Ci1和Ci2为第i段微分待定常数。

考虑计算方便，取计算图示为全填充型溶洞，如图7 所示，图中1 和3 中2 段为岩层，2 段为全填充型溶洞，锚索在A和B两截面为岩层与溶洞的分界，岩层与溶洞填充物仅有剪切刚度的不同。

图7 全填充型溶洞锚固体剪应力分布图Fig. 7 Shear stress distribution diagram of anchor solid in fully filled karst cave

设锚索1，2，3 段剪切刚度分别为k1，k2，k3，则根据式(9)得：

当z=0时，由式(11)，第1段锚固体有：

当z=x时，对第1，2段锚固体，剪切位移与轴向力是相等的，由式(11)和式(12)：

同理当z=x+s时，第2，3段锚固体有：

当z=L时，由式(11)，第3段锚固体有：

当锚固体周边剪应力超过其弹性极限黏结强度时，界面将发生滑动破坏。故计算锚索穿越溶洞锚固力时，以锚固始端剪应力达到弹性极限黏结强度时锚固体的轴力值作为锚索锚固力值。根据式(12)，有：

式中：τ1为第1 段锚固体弹性极限黏结强度；G1s为第1段锚固体周边岩体的剪切模量。

联立以上(13)～(19)各式，可得最终锚索穿越全填充型溶洞锚固力P为：

分析式(20)及(21)可知，长锚索穿越溶洞锚固力的计算相较一般地层增加溶洞与锚索的位置关系、溶洞直径以及溶洞填充物的力学参数。因此，确定这几项参数后便可以运用公式(20)进行长锚索穿越溶洞时锚固力的计算，定量分析在特定的岩溶条件下锚索锚固力是否能达到设计值。

以上分析建立了锚索穿过全填充型溶洞时锚固力的计算方法，对于锚索穿过无填充型溶洞的情况，同样如图7 所示，只需令溶洞段k2，τ2为0，仍按照全填充型溶洞的计算方法进行计算。当锚索穿过半填充性溶洞时，可将溶洞段进行细分，分为若干子锚固段，这样就可将溶洞段分为若干不同小段的全填充型和无填充性溶洞进行分别计算。限于篇幅原因，本文不过多赘述。

上述公式是假设锚固体及其周围岩土体为弹性介质、且无相对滑移推导得到，因此式(20)及(21)适用于易出现溶洞的均质岩土体，如石灰岩、白云岩及泥灰岩等。

2.3 计算方法的验证

2.3.1 工程概况

选取徐州地铁2 号线淮塔东路站基坑里程K11+400.000 断面进行验证。下伏基岩为中风化灰岩，岩层下含有直径为1 m 的全填充型溶洞，充填物为硬~可塑状褐黄黏土[24-25]，夹灰岩、泥灰岩碎块。锚固体半径r0为0.075 m，弹性模量为3.02×104MPa，锚固体弹性极限黏结强度τ1为150 kPa。锚固段岩层剪切模量G1s=G3s=45 MPa，泊松比μ1s=μ3s=0.3，溶洞填充物的泊松比μ2s为0.36，剪切模量G2s为4 MPa。锚索选取第2 道锚索，自由段Lf=5 m，锚固段长度La=9 m，其中第1 段锚固体长度为6 m。锚索选用3φs15.2钢绞线，钢绞线标准强度1 860 MPa，锚索轴向拉力设计值180 kN。

2.3.2 实测与计算结果对比

对第2道穿越溶洞的锚索进行抗拔试验，溶洞与锚索位置关系如图8所示。试验中采用千斤顶进行渐进逐级加载，如图9 所示。本试验共进行3次，当锚索锚固力趋于稳定时，读取得到锚索锚固力的值分别为185.67，185.89 和184.82 kN，平均值为185.46 kN。采用本研究所建立的计算方法，将现场相关地层与锚固体参数代入计算公式，得到锚固力值为213.88 kN。

图8 第2道锚索与溶洞位置关系Fig. 8 Position relationship between the second anchor cable and the karst cave

图9 锚索拉拔试验示意图Fig. 9 Schematic diagram of anchor cable pulling experiment

锚索的特征荷载包括锚索工作荷载与极限荷载，工作荷载指锚索正常工作时所承受的拉拔荷载，而极限荷载指锚索所能承受的最大荷载[26]。现场实测时，锚索未达极限值，尚属工作荷载。理论计算时，以锚固始端黏结强度达到其弹性极限黏结强度，锚固体与岩体即将发生相对滑移得到，理论计算结果为锚索弹性极限锚固力，属极限荷载。根据《建筑基坑支护技术规程》(JGJ120—2012)[27]，锚杆(索)极限抗拔承载力与其轴向拉力标准值之比，即为抗拔安全系数，不应小于1.4。江冠等[26]根据现场6 根锚索实测，得到极限荷载与工作荷载比值范围为1.1～1.3。

当理论计算极限荷载213.88 kN 时，根据规范计算理论值对应的工作荷载为152.77 kN，由江冠的研究，可得对应的工作荷载164.53～194.44 kN。而现场实测值为185.46 kN，与规范相比偏安全，而与江冠等现场实测数据吻合较好，因此本研究所提计算方法可为岩溶地层地铁车站长锚索穿越溶洞锚固力的计算提供参考。

3 锚索穿越溶洞锚固力影响因素分析

为研究锚索锚固力受岩溶条件的影响程度，由以上锚索锚固力计算公式可知，共有α1，α2，α3，x及s5 个参数，由于α1和α3为岩层段与剪切刚度有关的量，一般没有变化，对最终结果影响不大，而α2与溶洞的填充物剪切模量相关，故考虑剪切模量G2s，即实际影响因素为锚固始端距溶洞的距离x，溶洞直径s及溶洞填充物的剪切模量G2s。其他参数同2.3.1节。

3.1 锚固始端距溶洞的距离的影响

取溶洞直径s分别为1，2，3 和4 m，根据上述锚固力公式，绘图得到锚索锚固力随锚固始端距溶洞距离x变化的曲线如图10所示。

图10 锚固力随锚固始端距溶洞的距离变化图Fig. 10 Anchoring force changes with the distance from anchorage beginning to the cave

单独分析每条曲线，即溶洞直径不变时，随着溶洞段距锚固始端的距离的增加，锚索锚固力的值逐渐增大，增长速率逐渐减小，最后趋于稳定。这与实际相符合，当x→+∞时，即锚固体穿过岩层长度无限长，此时溶洞对锚固力影响不大。由图10易得，当溶洞直径s分别为1，2，3和4 m，锚固始端距溶洞距离x≥2.3，2.6，2.8 和2.9 m 时，锚索锚固力即可达到设计值180 kN。

横向比较各条曲线，对于相同的锚固始端距溶洞距离，随着溶洞直径的增大，锚固力将有一定程度降低。当溶洞直径不超过2 m，即s≤2m时，当溶洞距锚固始端的距离大于4 m，锚索的锚固力均不低于200 kN；而s＞2 m 时，锚索的锚固力不全大于200 kN。

当溶洞段距锚固始端的距离为0.5 m 时，锚索的锚固力均不超过110 kN。而当溶洞距锚固始端的距离大于4 m，锚索锚固力均不低于180 kN。故当溶洞分布在距锚固始端较近的位置(4 m 内)时，锚固力的值受溶洞的影响很大，在此之外的溶洞对锚索锚固力的影响较小。究其原因是锚索的剪应力值在锚固始端是最大的，剪应力主要分布为指数递减曲线，主要集中在始端附近，锚固始端较近的区域越长，剪应力分布范围越广，所得的锚固力值也就越大。

3.2 溶洞直径的影响

取锚固始端距溶洞的距离x分别为1，2，3 和4 m，得到锚索锚固力随锚固始端距溶洞距离x变化的曲线如图11所示。

图11 锚固力随溶洞直径变化图Fig. 11 Anchorage force changes with the diameter of karst cave

单独分析每条曲线，当溶洞段距锚固始端的距离不变时，随着溶洞直径增加，锚索锚固力的值逐渐减小。当溶洞段距锚固始端的距离分别为x=1 m，2 m，无论溶洞直径多大，锚索的锚固力均不能达到设计值180 kN 的要求。而当溶洞段距锚固始端的距离x=3 m，溶洞直径只需s≤4.3 m，锚索锚固力即可以达到设计值180 kN 的要求，这表明，对于特定的溶洞，可根据溶洞直径来确定最小锚固始端距溶洞的距离。而当溶洞距锚固始端的距离x≥4 m，此时无论溶洞直径多大，锚固力变化不大。溶洞直径对锚固力影响较小，锚固力能满足设计180 kN要求。

横向比较各条曲线，对于同一溶洞直径s，随着锚固始端距溶洞的距离x的增大，锚固力逐渐增大。且随着溶洞直径的增大，锚固力差值增加更加显著。因此，在实际工程中应保证锚固始端距溶洞距离尽量大，以确保基坑工程的稳定性。

3.3 溶洞填充物剪切模量的影响

为分析溶洞填充物剪切模量G2s对锚索穿过溶洞时锚固力的影响，取溶洞段距锚固始端的距离x=2 m，溶洞直径s=2 m，填充物剪切模量G2s变化范围为1～45 MPa，其他参数与上述保持一致，得到锚索锚固力随溶洞填充物剪切模量G2s的变化曲线图，如图12所示。

图12 锚固力随溶洞填充物剪切模量变化图Fig. 12 Anchoring force changes with shear modulus of cave filling

由图12 可知：当溶洞直径和溶洞距锚固始端的距离不变时，随着溶洞填充物剪切模量的增大，锚索锚固力的值逐渐增大，大致趋势为线性增长。当溶洞填充物剪切模量大于25 MPa 时，锚固力已经达到了180 kN 的设计值。因此，当溶洞填充物剪切模量足够大时，锚索穿过溶洞时，不用对溶洞进行注浆填充，锚索锚固力也能达到设计要求。这与实际相符，当锚固力不满足设计要求时，常进行注浆加固，而注浆加固实质就是提高溶洞填充物的剪切模量。

4 结论

1) 基于剪切位移法原理，采用荷载传递法，考虑锚固体穿过溶洞时，分界处的变形协调与力的平衡关系，建立岩溶地层车站基坑长锚索穿越溶洞时锚固力的计算模型，推导得到相应的长锚索锚固力计算方法，通过与实际现场测试的锚固力对比，理论计算方法与实际吻合较好，计算方法可为长锚索穿越溶洞锚固力的计算提供参考。

2) 当溶洞直径不变时，随着溶洞距锚索锚固始端距离的增大，长锚索的锚固力也逐渐增大，当溶洞距锚索锚固始端距离小于4 m 内时，溶洞对锚索锚固力的影响很大，而在4 m外影响较小。

3) 当溶洞距锚索锚固始端距离不变时，随着溶洞直径增大，长锚索的锚固力逐渐减小，当溶洞直径较大且锚固始端距溶洞小于3 m 时，必须对溶洞进行注浆加固，以使锚索的锚固力达到设计要求。

4) 当溶洞距锚索锚固始端距离和溶洞直径均不变时，随着溶洞填充物剪切模量的增大，长锚索的锚固力也逐渐增大。计算分析表明，在溶洞段距锚固始端的距离x=2 m，溶洞直径s=2 m 该工况下，当溶洞填充物的剪切模量大于25 MPa 时，锚索锚固力达到设计值，可以直接穿过溶洞进行锚固施工。而当填充物的剪切模量较小时，采用注浆方式填充溶洞可有效提高锚索的锚固力。