套利限制对股票错误定价的影响研究
杨驰张兵朱红兵
(1.南京大学商学院,江苏 南京 210000;2.河海大学商学院,江苏 南京 210000)
一、引言
市场定价效率一直是学术界研究的重要话题。中国股市发展时间较短,个人投资者占比高,追涨杀跌等非理性行为较为突出。在指数层面,2014年6月至2015年6月上证指数上涨157.55%,随后却在半年内下跌49.1%,在较短时间内出现剧烈波动,远超同期其他主要国家股票市场水平。在个股层面,以贵州茅台为例,作为盈利增速较为稳定的股票,在2021年初利润增速为10%左右的情况下,其PEG达到7倍左右;在估值高的情况下,股价却偏离其实际价值。股指及个股的表现表明中国股票市场定价效率较低,错误定价现象存在。行为金融学对错误定价的解释表明,当股价偏离其真实价值时,套利活动受到诸多限制,无法使股票价格收敛于真实价值,导致市场定价效率降低,进而引发错误定价。相较于其他主要资本市场,中国股票市场套利活动面临的限制更为复杂:T+1交易制度、涨跌幅限制以及缺乏全面做空机制等特点都在一定程度上阻碍了套利行为;由于信息披露制度尚不完善、散户比例较高等原因,套利活动面临的各类风险也较为显著。因此,相较于其他主要资本市场,中国股市由套利限制引发的错误定价现象更为显著,如何减轻套利限制以提高市场定价效率成为了亟待解决的问题。
监管部门近年来进行了多项基础制度改革。2010年3月,沪深交易所正式启动融资融券业务,并经七次扩容将融资融券标的股票数量提升至2200只,对应标的股可以融券卖空,降低了卖空限制。上交所科创板和深交所创业板首批注册制企业分别于2019年7月和2020年8月上市交易,将股票涨跌幅限制由10%扩大到20%,相关股票在上市首日起即可作为融资融券标的。2021年9月成立的北交所将股票涨跌幅限制进一步放宽至30%。当股价在当日触及涨跌幅限制时,投资者无法以更高或更低的价格进行正向交易,而不断放宽的涨跌幅限制有利于套利活动的进行。2010年后,中金所陆续推出沪深300等股指期货,投资者得以做空股指期货,在一定程度上为股指期货对应指数的成份股减轻了卖空限制。2021年5月,证监会发布了最新的《上市公司信息披露管理办法》,进一步完善了信息披露基本要求,提高了信息透明度,从而降低了交易风险。上述一系列举措使套利限制有所缓解。然而,各类套利限制对错误定价具有不同程度的影响,何种套利限制起主导作用尚不明确,这给监管部门改革的效果带来了不确定性。因此,厘清中国股市套利限制的类型、研究各类套利限制对错误定价的差异性影响,可以填补套利限制对错误定价影响分类研究的空白,为监管部门提供针对性政策建议,具有重要的理论价值和现实意义。
本文的边际贡献主要有两点。第一,从形成套利限制的基础要素出发,对A股市场的套利限制进行分类,首次研究不同维度套利限制对中国股市错误定价的影响,分析何种套利限制的影响起主导作用,并创新性考虑T+1交易制度的约束作用。已有文献虽然研究了某类套利限制与错误定价的关系,但甚少关注套利限制这一复杂体系的全貌,在客观评价套利限制对错误定价的影响上具有一定的局限性(林思涵等,2020;李科等,2014)[21][20]。少数文献虽对套利限制进行了分类,但其套利限制的涵盖范围不够全面(孔东民,2008;陈慰等,2018)[19][16]。现有文献未考虑中国股市T+1交易制度所引发的套利限制。该制度下,当日买入的股票无法在当日卖出,阻碍了股票的日内正常流通(Zhang,2020)[14]。此外,形成不同维度套利限制的基础要素各不相同,其对错误定价的影响具有差异性,何种套利限制起主导作用尚不可知。总体上,现有文献缺少套利限制对错误定价影响的分类研究。因此,有必要进行分类研究以求更加深入认识套利限制对错误定价的影响。
第二,分析了不同估值情形下各细分维度套利限制对错误定价的影响,从投资者买卖行为的角度揭示了相关机制,并进行了其他异质性分析,增加了研究的深度。现有文献虽然分析了不同估值情形下套利限制对错误定价影响的差异性(Guidolin and Ricci,2020;尹玉刚等,2018)[4][25],但缺乏深入的机制分析。本文基于不同维度套利限制的视角,分别分析了不同估值情形下套利限制对错误定价产生异质性影响的背后机制,丰富了该领域的机制研究。
二、文献梳理和研究假设
(一)文献梳理
目前,相关文献对股票套利限制的度量尚无统一标准。孔东民(2008)[19]使用套利风险、可对冲风险、交易成本和投资者熟练度这四个指标衡量套利限制,并采用成交额这一指标间接测度交易成本。叶建华和周铭山(2013)[24]分别采用股价同步性、机构持股比例、会计盈余质量及Amihud非流动性指标来衡量套利风险、投资者成熟度、信息透明度和套利成本等四个套利限制因素。Gu et al.(2018)[3]使用六个套利限制指标分别构建虚拟变量,取其算术平均数构建了综合套利限制指标——Gu指标。虞文微等(2017)[26]借鉴了Gu指标的构建方法,构造的股票套利限制因子主要包括是否触及价格涨跌幅限制、是否属于融资融券标的、是否属于股指期货对应指数的成份股、非流动性以及交易量。陈慰等(2018)[16]从套利风险的角度对套利限制进行衡量,使用分析师覆盖和现金流波动性衡量基本面风险,使用股权分散度和特质波动率衡量噪音交易者风险。Lee et al.(2019)[8]使用特质波动率指标衡量套利限制。
上述文献对套利限制成因的探讨主要集中在三个方面,即形成套利限制的基础要素有三类:交易成本、交易风险和交易约束。一是交易成本。套利活动需要进行相应的交易,交易产生的成本是导致套利限制的一大原因。以交易佣金和印花税等为代表的直接交易成本可视为固定值,因而上述文献多以Amihud非流动性指标和成交额(量)这类股票流动性指标间接测算交易成本,股票流动性越好则交易成本越低。二是交易风险。套利活动存在相应的风险。既有研究指出,套利者主要面临噪音交易者风险和基本面风险两类,本文称之为交易风险,以这两类风险的相关指标进行度量。三是交易约束。套利活动受到中国股票市场交易制度的约束。相关文献多从股票是否触及价格涨跌幅限制、是否属于融资融券标的以及是否属于股指期货对应指数的成份股等三个角度进行衡量。本文创新性地将T+1交易制度也纳入指标体系,将交易制度导致的套利限制称为交易约束。综上所述,本文将套利限制分为交易成本、交易风险和交易约束三类细分维度,使用Gu et al.(2018)[3]的方法分别计算三类细分维度的套利限制,并据此计算综合套利限制。
股票的真实价值难以测度,一些学者采用股利倍数法和现金流折现法等方式确定公司的基础价值,当股价偏离基础价值就会出现错误定价现象。Vuolteenaho(2002)[13]认为上市公司现金流可以反映股票的真实价值,股票价格偏离现金流折现的部分就是错误定价。然而,中国上市公司具有分红率较低等特点,股票市场的信息披露制度也不够健全,基础价值的测算具有模糊性。股票的估值还可以从收益率的视角进行间接测度。由于套利行为的影响,对于高估股票,股票价格将下跌,股票未来收益率为负;对于低估股票,股票价格将上涨,股票未来收益率为正。因此,能预测股票收益率的相关指标便可以用于测度股票错误定价。若该指标越大,股票未来收益率越高,股票价格越低估,反之亦反是。
学者们不断发现各类股票市场异象可以用于预测股票收益率,更多的学者使用异象特征值来衡量股票错误定价。关伟和张晓龙(2017)[17]认为我国A股市场分红率低,因此,国外文献使用较多的剩余价值模型不再适用于中国市场,转而采用可操控性应计利润来度量股票错误定价。Stambaugh et al.(2015)[12]分别使用代表股票估值水平的11种异象特征值,按照百分位排名越高代表股票估值越高的方式对所有A股进行排序,将每一个排序结果进行标准化处理,计算11个排序结果的算术平均值来度量错误定价。有学者发现,部分异象在发达国家股市显著存在,但在中国股市并不存在(Han and Shi,2022;Jansen et al.,2021)[5][7],照搬其他资本市场的异象来衡量中国股票市场的错误定价显然具有一定缺陷。
Han et al.(2022)[6]分别使用CAPM模型、Fama-French三因子模型、Carhart四因子模型和Fama-French五因子模型计算出每只股票的alpha值,将四种alpha值的算术平均值作为错误定价的代理变量。alpha值为正、代表股价低估,alpha值为负、代表股价高估。alpha指标较为成熟,被广泛应用于业绩评估,可以很好地衡量错误定价(Berk and Van Binsbergen,2016)[2]。综上所述,本文主要使用alpha指标来构建错误定价指标,并参照Stambaugh et al.(2015)[12]的方法,使用异象特征值构建错误定价指标进行稳健性检验。
(二)研究假设
有关套利限制对错误定价影响的相关研究主要从单一类型套利限制的角度展开。王一鸣和周泳光(2022)[23]认为流动性的缺乏增加了投资者的交易成本,导致中国资本市场无效性增强,引起价格剧烈波动,造成错误定价。Shleifer and Vishny(1997)[11]认为,噪声交易者的非理性行为会造成股票价格在短期内持续偏离真实价值,无法在套利者的投资期限内得到纠正,从而引起错误定价。李科等(2014)[20]发现卖空限制导致了股价高估,融资融券制度等做空机制有助于矫正股价高估,提高市场定价效率。林思涵等(2020)[21]通过分析发现,融资融券交易制度在一定程度上能吸收投资者情绪的变化,进而纠正股票错误定价。
上述文献表明,流动性的缺乏增加了交易成本,从而加剧了错误定价程度。噪音交易者风险的提升加剧了错误定价。卖空限制对错误定价具有显著的正向影响,而采用融资融券等减轻套利限制的交易制度可以有效纠正错误定价。流动性属于交易成本的范畴,噪音交易者风险属于交易风险的范畴,卖空限制等属于交易约束的范畴,各细分维度套利限制对错误定价可能均具有显著正向影响。
目前的文献尚未研究何种套利限制对错误定价的影响起主导作用。由于中国股票市场的多种制度约束,如T+1交易制度、涨跌幅限制等在其他主要资本市场中均不存在,交易约束对错误定价的影响将显著大于其他资本市场。以中国股票市场的T+1交易制度为例,朱红兵和张兵(2020)[27]发现T+1交易制度产生了较高的制度成本,该制度使得当日买入的股票在当日不能卖出,导致隔夜收益率平均每年折价达11.91%。此外,Qiao and Dam(2020)[10]发现中国的T+1交易制度使得每日隔夜收益率折价达0.14%。基于以上学者的结论,同时结合中国股票市场与国外股票市场的差异,本文推测交易约束在影响错误定价的各细分维度套利限制中起主导作用,提出假设:
H1:交易约束在对错误定价具有正向影响的各细分维度套利限制中起主导作用。
在中国股票市场,有学者发现在不同估值情形下,交易风险对错误定价的影响存在更为显著的不对称性。柳楠等(2014)[22]发现交易风险和错误定价之间存在显著相关性。在低估情形下,交易风险与错误定价呈现负相关关系;在高估情形下,二者呈现正相关关系,交易风险在一定程度上可以解释错误定价。此外,在不同估值情形下,交易约束对错误定价也具有显著的不对称影响。林思涵等(2020)[21]、尹玉刚等(2018)[25]认为中国股票市场存在卖空约束,做多股票比卖空股票更加便捷。因此,对高估值股票进行卖空,进而修正错误定价的难度也将更大。对于不同估值水平的股票,以交易制度约束为代表的套利限制对错误定价的影响可能也不相同。
综上,已有学者发现在不同估值情形下,交易风险和交易约束对我国股票错误定价具有不对称的影响。具体而言:我国散户投资者占比高,套利者的力量相对较小,当股票价格下跌并进入低估区间时,大量非理性的投资者将恐慌出逃。此时,涨跌幅限制、T+1交易制度以及不可融券做空等交易制度将阻止投资者的非理性卖出行为。虽然交易约束的增加在一定程度上也对套利者的做多行为造成不利影响,但在非理性投资者占主导的市场中,交易约束依旧能减少错误定价的产生。同理,较大的交易风险也会使得非理性卖出行为和套利者的做多行为同时受到约束,但对非理性卖出行为的约束更大。因此,股票低估时交易风险和交易约束与错误定价之间呈现负相关关系。当股价上涨、变得高估时,若交易约束增大,套利者的卖空行为受到制约,股票价格将难以回归真实价值,股票价格进一步升高,错误定价加剧。此外,当股票价格高估后,交易风险的增加会引来博彩型投机者的大量买单,同时抑制套利者的卖空行为,造成股价进一步高估,加剧错误定价程度。因此,股票高估时交易风险和交易约束与错误定价之间呈现正相关关系。
不同估值情形下交易成本对错误定价的影响也可能具有较大差异。现实市场中,股价被低估时成交萎靡,若此时降低交易成本将增加投资收益,吸引资金入场,促进股价上涨,降低错误定价程度。当股价被高估时,交易成本的增加可以打击投机活动,降低错误定价程度。例如我国在2007年5月将证券交易印花税由0.1%提高至0.3%,以此给当时的非理性投机行为降温;在2008年4月又将印花税再次调整为0.1%,以求提振萎靡的股市。Nneji(2015)[9]认为流动性的增加会引起股价泡沫的增长,而流动性的增加能降低交易成本。基于现实市场情况和上述文献可以推断:在低估阶段,流动性的增加降低了交易成本,促使投资者买入股票,促使股价上涨,减轻错误定价;在高估阶段,流动性的增加降低了交易成本,促使投资者买入股票,促使股价进一步上涨,加剧错误定价。因此,低估情形下交易成本与错误定价之间呈现正相关关系,高估情形下交易成本与错误定价之间则呈现负相关关系。
根据以上文献和分析,本文提出假设:
H2:高估情形下,交易成本与错误定价之间呈负相关关系,交易风险和交易约束与错误定价之间呈正相关关系;低估情形下,交易成本与错误定价之间呈正相关关系,交易风险和交易约束与错误定价之间呈负相关关系。
三、变量描述和模型设定
(一)样本选择和数据来源
本文研究对象为所有沪深A股。融资融券制度和股指期货制度均从2010年开始实施,所以样本时间区间为2010年1月至2020年12月,相关变量均为月频数据。本文剔除风险警示类和金融行业股票数据。为排除极端值的影响,对相关变量进行上下1%分位的缩尾处理。本文所使用的无风险利率和因子数据来源于中央财经大学中国资产管理研究中心网站,其余数据来自于Wind数据库和CSMAR数据库。
(二)变量构造
1.因变量的构造及计算
本文的因变量为错误定价,指标使用alpha指标进行计算,相关处理方式如下:
首先,分别使用滚动前1~60月的月度超额收益率对CAPM模型、Fama-French三因子模型、Carhart四因子模型和Fama-French五因子模型,即式(1)~(4),进行回归,得到相应的回归系数:
其中,retrf表示超额收益率,MKT表示市场因子,SMB表示规模因子,HML表示价值因子,UMD表示动量因子,RMW表示盈利因子,CMA表示投资因子。
然后,将上述回归得到的自变量回归系数β^、γ^、θ^和δ^代入原模型,并代入各期的自变量和因变量数值,计算出各因子模型的每期alpha值,分别为CAPMα、FF3α、CHTα和FF5α。最后将由四个因子模型得到的alpha值按时间截面计算算术平均值compα,作为本文所需要的alpha指标。具体做法分别见式(5)~(9):
高估和低估均表示股票价格偏离其真实价值。高估或低估的程度越大,股票价格偏离其真实价值的程度就越大,股票的错误定价程度也就越大。alpha值大于0表示低估,小于0表示高估。alpha值的绝对值越大,代表股票高估或者低估的程度越大,错误定价程度也就越大。本文使用compα的绝对值表示错误定价程度misp,计算方法见式(10):
2.核心自变量的构造及计算
本文的核心自变量为交易成本、交易风险、交易约束以及综合套利限制,具体计算方式如下:
(1)交易成本(cost)
交易成本(cost)使用Amihud非流动性指标(Amihud,2002)[1]、相对有效价差(蒋先玲和徐海洲,2015)[18]和交易量等三个衡量流动性的指标计算得来。其中,Amihud非流动指标越高,交易成本越高;相对有效价差越大,交易成本越高;交易量越大,交易成本越低。本文计算当月所有交易日相应数据的算术平均值得到Amihud非流动性指标和相对有效价差的月频数据,成交量也为月频数据。
将这三个指标以月为基准,按指标大小分为五组,并分别按照相应指标所对应交易成本的高低进行五级打分,交易成本高的组得5分,次高组得4分,依次降低,直至最低组得1分。将上述得分进行差分标准化处理,将数值标准化为0~1,数值越大,交易成本越高。参考(Gu et al.,2018)[3]的做法,计算出三个指标的算术平均值作为交易成本指标。
(2)交易风险(risk)
交易风险(risk)包含了基本面风险和噪音交易者风险。本文参考陈慰等(2018)[16]的做法,使用现金流波动率和分析师覆盖两个指标衡量基本面风险。由于个人交易者更多被看作是噪音交易者,机构投资者更多被看作是理性投资者(陈其安等,2010)[15],因而投资者结构可以用来间接测度噪音交易者风险。使用户均持股比例和机构持股比例来衡量投资者结构。特质波动率反映出非系统性风险,也可以用来衡量噪音交易者风险(陈慰等,2018)[16]。因此,使用特质波动率、机构持股比例和户均持股比例三个指标衡量噪音交易者风险。其中,现金流波动率越高,交易风险越高;分析师覆盖越高,交易风险越低;特质波动率越高,交易风险越高;机构持股比例越高,交易风险越低;户均持股比例越高,持股集中度越高,散户占比越低,交易风险越低。
本文按月将股票日收益率以三因子模型进行回归,并计算出残差项的标准差,以此测度股票的特质波动率。股票分析师覆盖数据仅有年度值,将年度数据赋值给该年所有月份。本文采用滚动10个季度(含当季)的方法计算上市公司经营活动所产生的现金流标准差,除以这10个季度现金流的平均值并取绝对值,以此测度季度现金流波动率,再赋值给该季度3个月份。机构持股比例和户均持股比例只有季度值,将相应季度数据赋值给该季3个月份。
将上述五个指标以月为基准,按大小分为五组,并分别按照相应指标所对应的交易风险高低进行五级打分,交易风险最高的组得5分,次高组得4分,依次降低,直至最低组得1分。将上述得分进行差分标准化处理,将数值标准化为0~1,数值越大,交易风险越高。计算出五个指标的算术平均值测度交易风险。
(3)交易约束(constrt)
交易约束(constrt)由股票是否属于股指期货对应指数的成份股、是否触及涨跌幅限制、是否属于融资融券标的(Gu et al.,2018)[3]和T+1折价率等四个指标构成。以当月是否属于股指期货对应指数的成份股、当月是否有交易日触及涨跌幅限制以及当月是否属于融资融券标的构建前三个指标的月度虚拟变量。若股票在当月属于股指期货对应指数的成份股,其交易约束更低,指标数值设为0;反之更高,指标数值设为1。若股票在当月存在触及涨跌幅限制的交易日,其交易约束更高,指标数值设为1;反之更低,设为0。若股票在当月属于融资融券标的,其交易约束更低,指标数值设为0;反之更高,设为1。T+1折价率可以反映股票受T+1交易制度的约束程度,本文参考(朱红兵和张兵,2020)[27]的做法计算股票的月度T+1折价率,用以度量T+1交易制度造成的套利限制。T+1折价率数值越低,表明折价程度越高,T+1制度造成的交易约束越高;反之越低。将T+1折价率以月为基准,按大小分为五组,并按照T+1折价率的高低进行五级打分,T+1折价率最低的组得5分,次低组得4分,依次降低,直至T+1折价率最高的组得1分。将得分进行差分标准化处理,将数值标准化为0到1区间,数值越大,受T+1制度影响越大,相应的交易约束越大。计算出四个指标的算术平均值衡量交易约束。
(4)综合套利限制(limit)
综合套利限制(limit)为上述三类细分维度套利限制指标的算术平均值。综合套利限制虽然不是本文的主要研究对象,但使用该指标可以从全局对套利限制进行分析,并验证各类套利限制指标和回归模型的稳健性。具体计算方式见式(11):
3.控制变量
本文构建基础回归模型所需要的控制变量有:Beta值、市值对数、账面价值与市值比、净投资额、ROE值、换手率、动量指标、短期反转指标和最大5日收益率均值。
主要变量定义如表1所示。
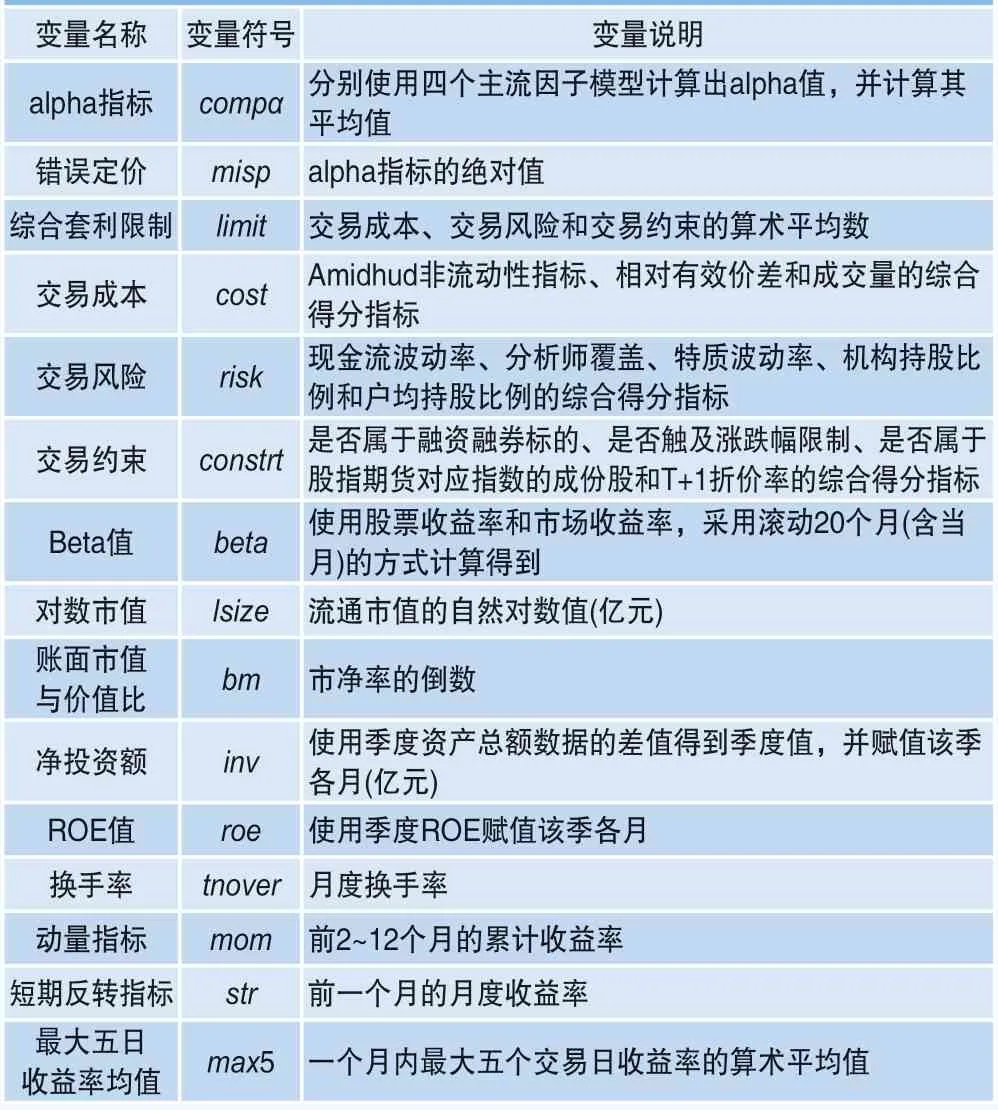
表1 主要变量定义
(三)模型设定
根据以上变量,本文建立了两个基础回归模型。回归模型(12)用于分析综合套利限制对错误定价的影响,模型(13)用于分析各细分维度套利限制对错误定价的影响:
(四)描述性统计
本文对主要变量进行描述性统计,结果如表2所示。alpha指标的最大值和最小值(在结果保留三位小数的情况下)绝对值大小相同,平均数接近于0,说明以alpha指标衡量股票估值,整体上既不会高估也不会低估,此指标是衡量股票估值的良好选择。交易成本、交易风险、交易约束以及综合套利限制的均值都在0.5附近,即在数值标准化后0~1区间的中点位置附近,四个指标均能较好度量套利限制。其余变量数值结果均无异常,数据质量较好。
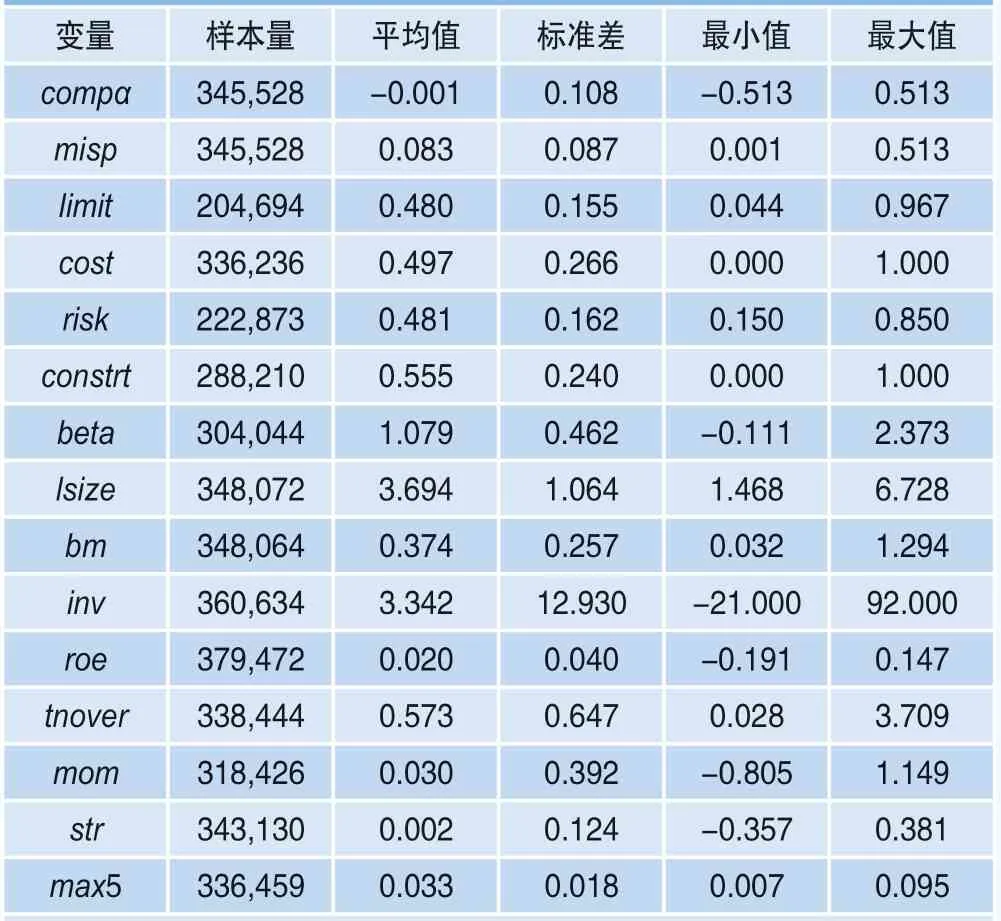
表2 变量的描述性统计结果
四、实证结果与分析
(一)相关性分析和核心自变量有效性检验
在回归分析前,本文先对解释变量进行Pearson相关性检验,以排除可能存在的多重共线性问题,并分析三类细分维度套利限制之间的相关性以检验套利限制的分类是否合理。综合套利限制、交易成本、交易风险、交易约束以及控制变量的Pearson相关性检验结果如图1所示。
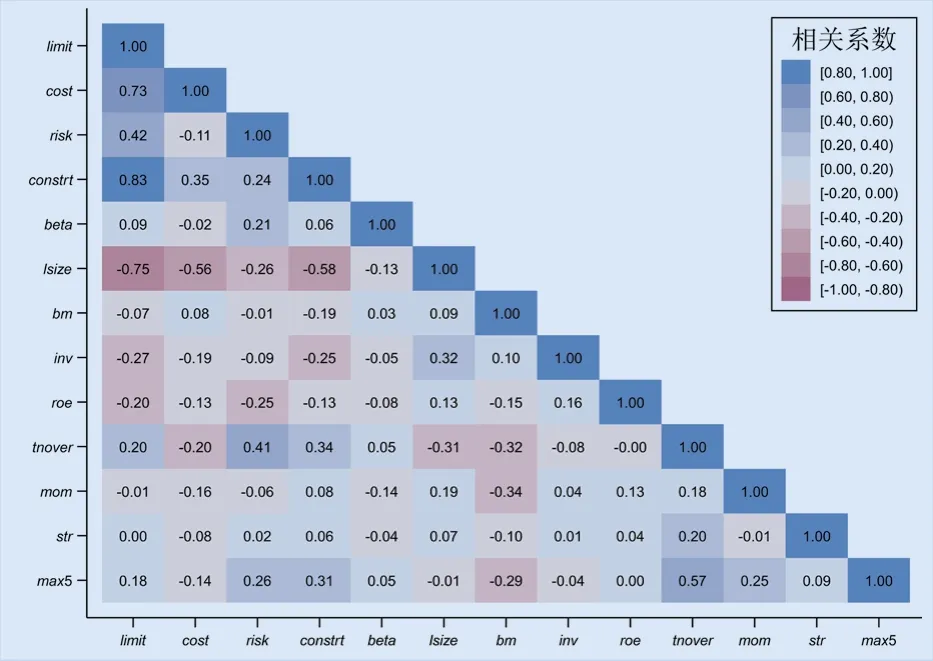
图1 主要解释变量的Pearson相关性检验结果
可以看出,三类细分维度套利限制之间的相关系数绝对值较小,相关性较弱,说明将套利限制划分为交易成本、交易风险和交易约束等三类细分维度是较为合理的。交易约束与综合套利限制之间的相关系数绝对值最大,交易成本与综合套利限制之间的相关系数绝对值次之,而交易风险与综合套利限制之间的相关系数绝对值则相对较小,说明本文计算的综合套利限制与交易约束的关联度最高,更多体现了交易约束的影响;综合套利限制与交易风险之间的关联性则相对较弱。总的来看,回归模型(12)和(13)自变量之间的相关系数绝对值基本都较小,相关性较弱,回归模型均不存在多重共线性问题。
为进一步证明核心变量即套利限制指标的有效性,本文通过分析不同特征股票组合的套利限制差异进行检验。通常小市值股票的套利限制大于大市值股票,非主板股票的套利限制大于主板股票。本文先按市值大小将股票分为五组,计算最小市值组、最大市值组的各类套利限制,并分析两组的套利限制差异。同样,将股票分为主板股票和非主板股票两组,分别计算其各类套利限制并分析两组的套利限制差异。上述所有指标均为月度数据,分组检验结果如表3所示。可以看出,无论是综合套利限制指标还是各细分维度套利限制指标,小市值股票组都显著大于大市值股票组。非主板股票组的综合套利限制、交易成本和交易约束都显著大于主板股票组,交易风险大于主板股票组但不显著。上述结果符合现实情况,说明各类套利限制指标能较好地度量相应套利限制,核心自变量是合理、有效的。
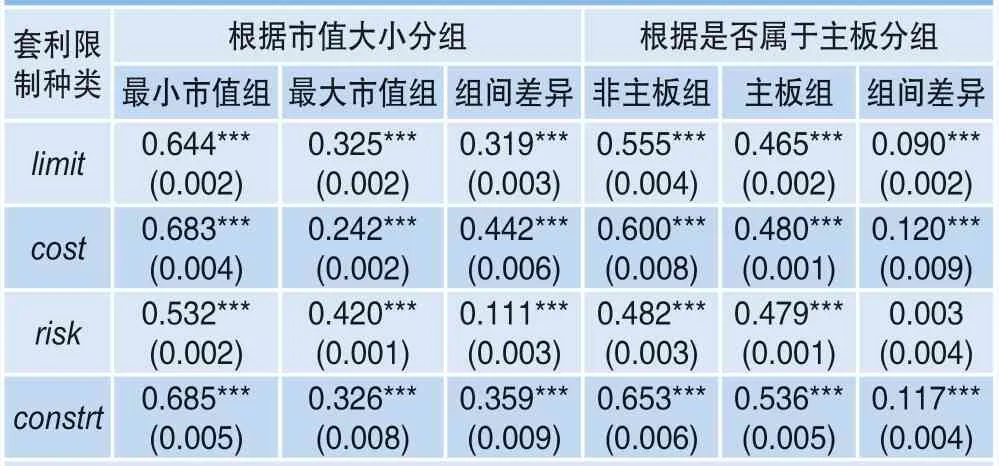
表3 根据市值大小和是否属于主板分组的各类套利限制
(二)套利限制对错误定价的影响分析
1.套利限制分组分析
本文分别使用综合套利限制以及三类细分维度的套利限制对错误定价进行分组分析,对套利限制与错误定价的关系进行初步判断。具体而言,使用各类套利限制对同期所有股票进行排序和五分组,构造五个套利限制组,按照等权的方式计算出各套利限制组的当期错误定价程度。按照套利限制从高到低的顺序,分别使用H、4、3、2、L表示各套利限制组。H-L表示最高套利限制组和与最低套利限制组的差值,具体结果如表4所示。
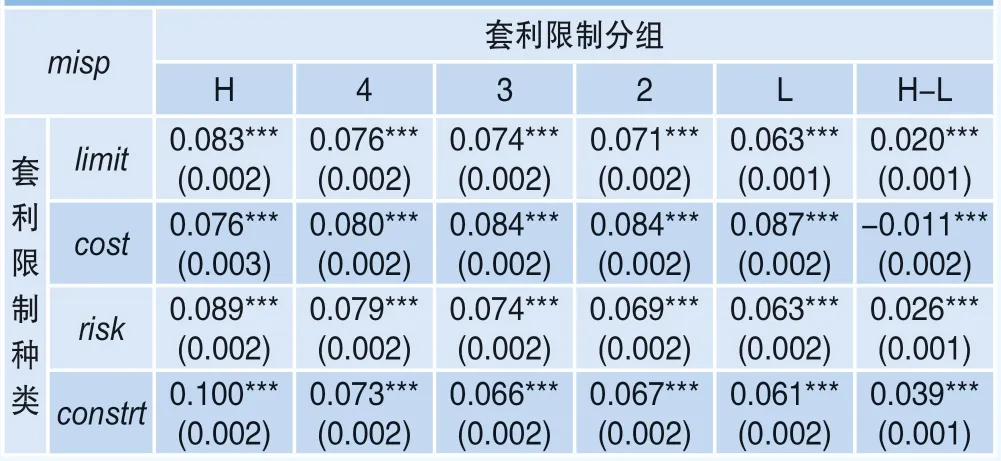
表4 基于套利限制分组的错误定价结果
可以看出,错误定价程度随着综合套利限制、交易风险和交易约束的增加而增加,但随着交易成本的增加而下降。对于综合套利限制,最高套利限制组的错误定价程度比最低套利限制组显著高0.02,高套利限制组的错误定价程度显著高于低套利限制组。同样,对于交易风险和交易约束,高套利限制组的错误定价程度显著高于低套利限制组。而对于交易成本,高套利限制组的错误定价程度显著更低。以上结果说明:套利限制与错误定价之间存在正相关关系。但分组分析忽略了其他因素的影响,为保证结论的可靠性,还需进行回归分析。
2.套利限制对错误定价影响的基础回归分析
为研究套利限制对错误定价的影响,本文用错误定价分别对综合套利限制以及各细分维度套利限制进行回归。由于套利限制指标是根据同一时间截面进行排序的相对指标,不同时间截面套利限制数值大小的比较没有实际意义,因此,本文采用Fama-Macbeth回归而非面板回归来进行分析,先使用模型(12)和(13)进行基础回归,并替换交易约束指标及综合套利限制指标进行稳健性检验。
具体而言,衡量交易约束的一个指标是是否属于股指期货指数的成份股,而股指期货一般很难用于个股对冲。为了排除该因素可能对结果造成的影响,将是否属于股指期货对应指数的成份股这一指标剔除后重新构造交易约束指标(nconstrt)。交易约束指标发生变化后,综合套利限制指标也会同步发生变化,本文使用nlimit表示新的综合套利限制指标。本文替换原模型中上述两个指标以进行稳健性检验。此外,为了证明错误定价指标的稳健性,本文参考Stambaugh et al.(2015)[12]的方法,构建了新的错误定价指标smisp,替换本文的misp指标进行检验。
回归结果如表5所示,列(1)为模型(12)的回归结果,列(2)为模型(13)的回归结果,列(3)为将模型(12)的limit指标替换为nlimit指标的回归结果,列(4)为将模型(13)的constrt指标替换为nconstrt指标的回归结果,列(5)(6)分别为将模型(12)(13)的misp指标替换为smisp指标的回归结果。
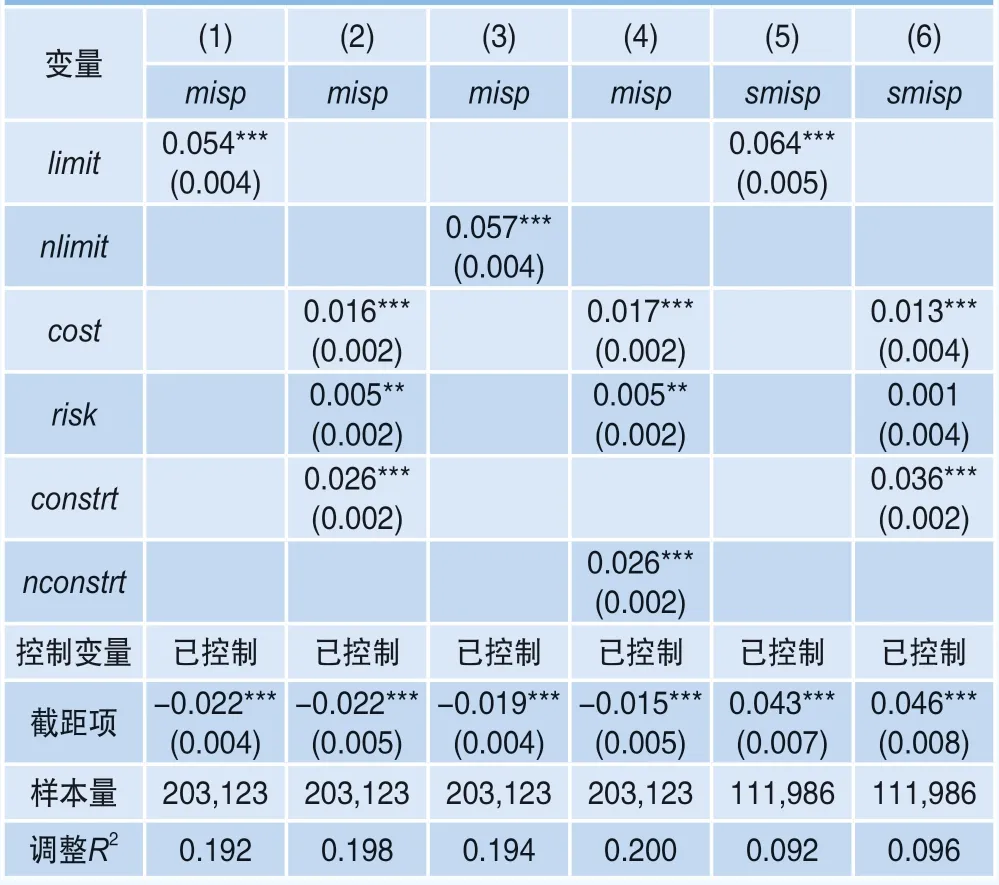
表5 套利限制对错误定价影响的基础回归结果
从列(1)可以看出,对于回归模型(12),综合套利限制对错误定价的影响显著为正。从列(2)可以看出,对于回归模型(13),交易成本、交易风险和交易约束对错误定价的影响均显著为正,交易成本和交易约束的回归系数较大,也更加显著。由于三类细分维度套利限制指标均进行了差分标准化处理,变量系数大小可以直接比较,因此,交易约束在对影响错误定价的各细分维度套利限制中起主导作用。
从列(3)(4)可以看出,使用nlimit和nconstrt指标替换原模型的limit和constrt指标后,各自变量的回归系数未发生显著变化。这说明加入或剔除是否属于股指期货对应指数的成份股这一指标对本文结论不会产生影响,进一步证明了套利限制指标的稳健性。从列(5)(6)可以看出,使用smisp指标度量错误定价后,综合套利限制对smisp的影响显著为正,各细分维度套利限制对smisp均具有正向影响,交易约束的影响依旧最强,交易成本次之,交易风险影响最小,与原回归模型的结论一致,因而使用alpha指标作为错误定价的度量有效且合理,结论较为稳健。因此,无论是综合套利限制还是各细分维度套利限制,对错误定价都具有显著正向影响。其中,交易约束在三类细分维度套利限制中起主导作用,假设H1成立。
此外,综合套利限制以及三类细分维度套利限制的回归结果都与市场现状及现有文献的研究相吻合,进一步说明三类细分维度的套利限制以及以此构建的综合套利限制是较为良好的指标,可以较好地达到研究目的。
3.不同估值情形下错误定价对套利限制的回归分析
为分析不同估值情形下套利限制对错误定价的影响,本文将股票分为高估和低估两个组进行分组回归分析。以compα为基准,compα大于0定义为低估值组,小于等于0定义为高估值组。采用Fama-Macbeth回归进行分析,具体结果如表6所示。
从表6列(1)(2)可以分析不同估值下综合套利限制对投资者错误定价的影响。低估情形下,综合套利限制对错误定价的影响为负,但不显著;高估情形下,综合套利限制对错误定价具有显著的正向影响。这说明从总体上看,中国股票市场套利限制对错误定价的正向影响在高估情形下比在低估情形下更加显著,在低估情形下套利限制对错误定价的影响相对有限。
从表6列(3)(4)可以进一步分析不同估值下各细分维度套利限制对错误定价的影响。低估情形下,交易成本的回归系数显著为正,交易风险和交易约束的回归系数显著为负;高估情形下,交易成本的回归系数显著为负,交易风险和交易约束的回归系数显著为正,且交易约束的系数更大。这说明在高估情形和低估情形下,对错误定价起主导作用的套利限制类型正好相反。在低估情形下,起主导作用的是交易成本;在高估情形下,起主导作用的是交易约束。根据组间差异检验结果,综合套利限制、交易成本、交易风险和交易约束系数的高、低估值组间差异均十分显著,因此上述结果是稳健的,符合中国市场的实际情况,也与现有文献的结论相吻合(林思涵等,2020;柳楠等,2014)[21][22],假设H2成立。
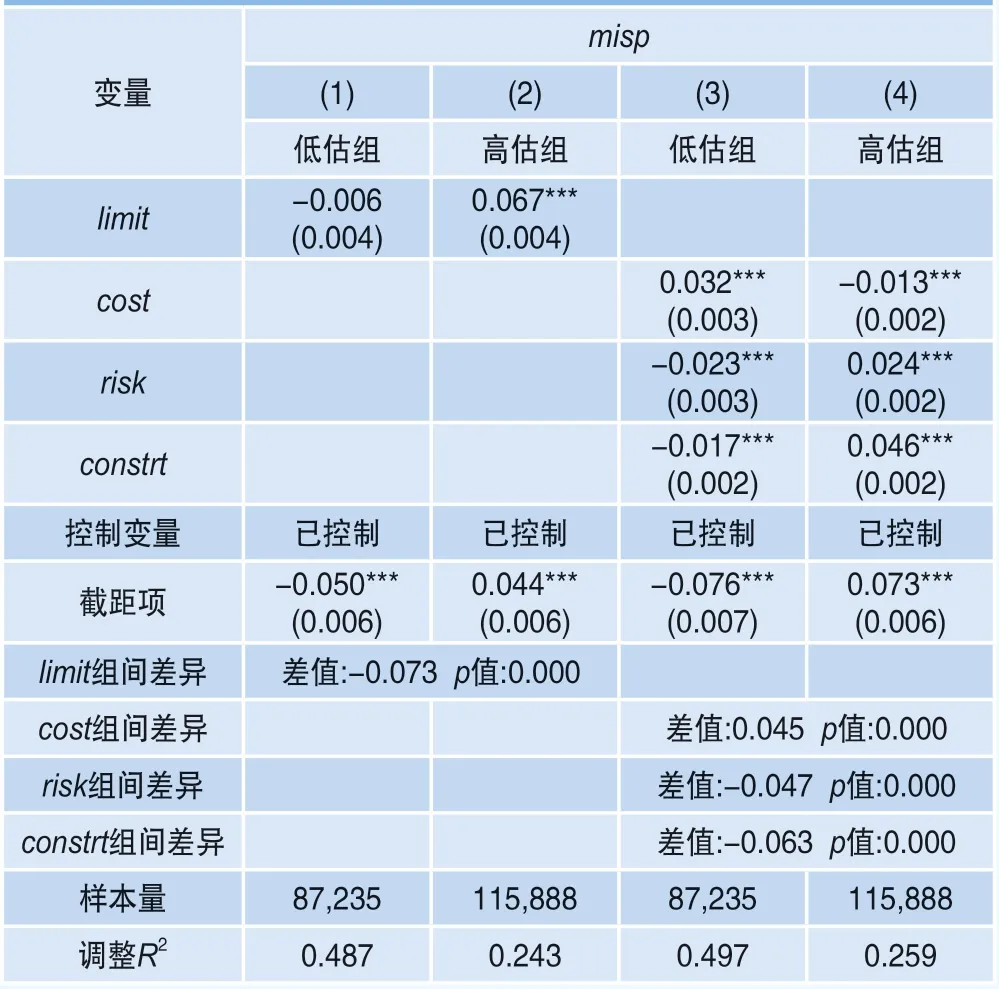
表6 不同估值情形下套利限制对错误定价的影响
4.不同投资者情绪下错误定价对套利限制的回归分析
行为金融学指出导致错误定价的原因主要有投资者非理性和套利限制两个层面。除套利限制外,投资者非理性也是影响错误定价的重要因素,但其是否会对套利限制与错误定价的关系产生影响尚不明确,可能会影响本文结论的稳健性。为排除投资者情绪可能造成的影响,本文以CICSI投资者情绪指标(使用CICSI指标计算的投资者情绪月度数据)进行分组,CICSI数值大于中位数的为高情绪组,小于等于中位数的为低情绪组,分别使用综合以及各细分维度套利限制对错误定价进行Fama-Macbeth分组回归,结果如表7所示。
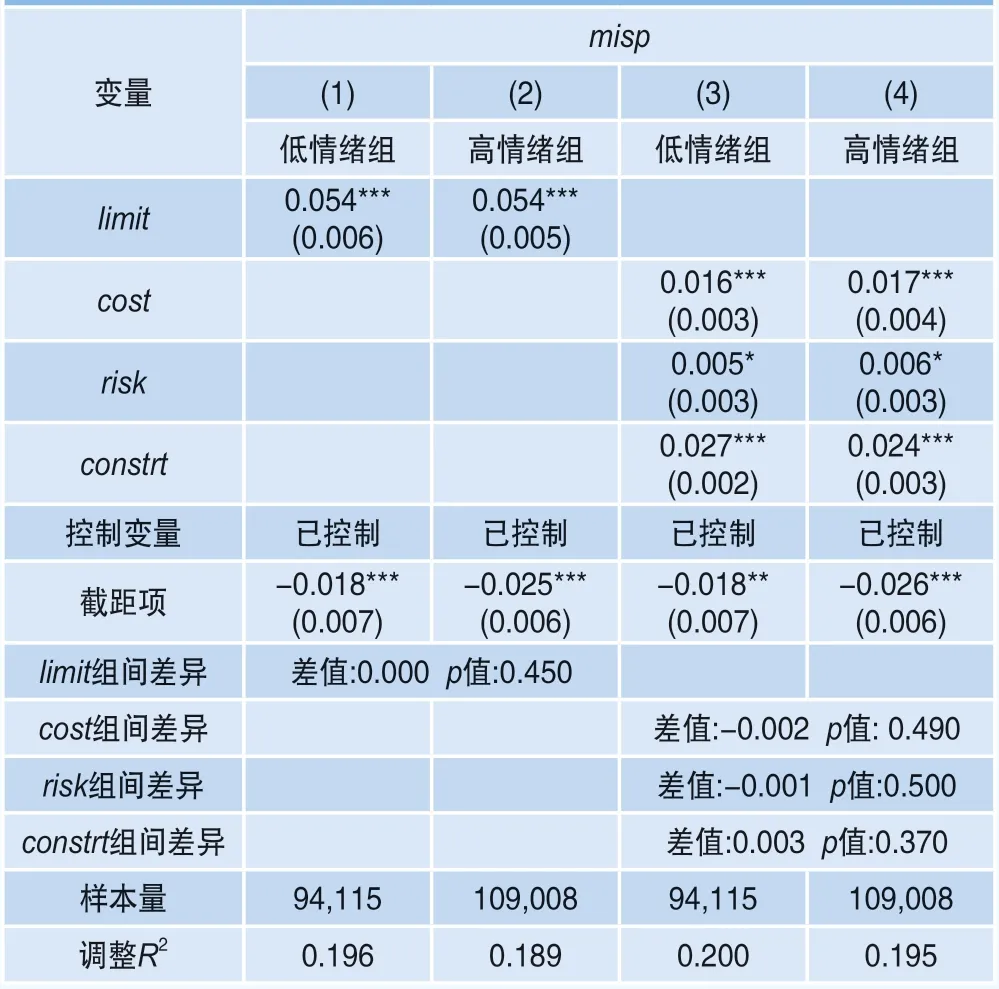
表7 不同投资者情绪下套利限制对错误定价的影响
可以看出,无论是高投资者情绪组还是低投资者情绪组,综合套利限制、交易成本、交易风险和交易约束对错误定价的影响均显著为正。根据组间差异检验结果,在不同投资者情绪下,综合套利限制以及各细分维度套利限制对错误定价的影响均无显著性差异。控制变量对错误定价的影响结果与基础回归保持一致,同样不受投资者情绪的影响,结果具有稳健性。
因此,不同投资者情绪下,各类套利限制对错误定价的影响无显著差异,说明各类套利限制对错误定价的影响并不受投资者情绪的干扰,实证结果是可靠的。
(三)套利限制对错误定价的影响机制分析
本文在理论分析中指出,在高估和低估情形下,各细分维度套利限制引起了投资者买卖行为的变化,进而会对错误定价产生影响。在本部分,本文通过识别在高估和低估情形下三类细分维度套利限制对股票主动买入(卖出)比率的影响,来分析套利限制如何影响投资者的买卖行为,以此研究套利限制对错误定价的影响机制。主动买入比率越高意味着投资者的买入意愿越大,主动卖出比率越高意味着投资者的卖出意愿越大。
首先计算每只个股的日度主动买入(卖出)比率。日度主动买入比率为当日主动性买入成交金额除以当日主动性买入成交金额与主动性卖出成交金额之和,日度主动卖出比率为当日主动性卖出成交金额除以当日主动性买入成交金额与主动性卖出成交金额之和,两者相加等于1。然后分别将个股的日度主动买入比率和日度主动卖出比率按月加总得到月度主动买入比率和月度主动卖出比率。此外,使用前文所述的alpha指标判定高估和低估情形。
使用交易成本对股票进行五分组以分析各组的主动买入比率及其差异。同样,分别使用交易风险和交易约束对股票进行五分组,分析各组的主动卖出比率及其差异。L组为各类套利限制最低组,H组为最高组,H-L为最高组与最低组的差值。buy表示主动买入比率,sell表示主动卖出比率,分组结果如表8所示。
可以看出,无论是在低估情形还是高估情形下,交易成本最高组与最低组的主动买入比率差值显著为负。这说明在低估情形下,交易成本越大,主动买入比率越低,投资者买入意愿下降,股票估值越难以回归真实价值,加剧了错误定价。在高估情形下,交易成本越大,主动买入比率越低,投资者买入意愿下降,阻碍了股票的进一步高估,减轻了错误定价。
此外,无论是在低估情形还是高估情形下,交易风险最高组与最低组的主动卖出比率差值显著为负。这说明在低估情形下,交易风险越大,主动卖出比率越低,投资者卖出意愿下降,阻碍了股票估值的进一步下跌,加剧了错误定价。在高估情形下,交易风险越大,主动卖出比率越低,投资者卖出意愿下降,使股票更加高估,减轻了错误定价。交易约束的结果与交易风险相同,不再赘述。
本文还使用Fama-Macbeth回归对上述结果进行了验证,分别分析在不同估值情形下各细分维度套利限制对主动买入(卖出)比率的影响。各回归模型的因变量为主动买入比率或主动卖出比率,核心自变量为各细分维度套利限制,并控制了其他控制变量,回归结果如表9所示。
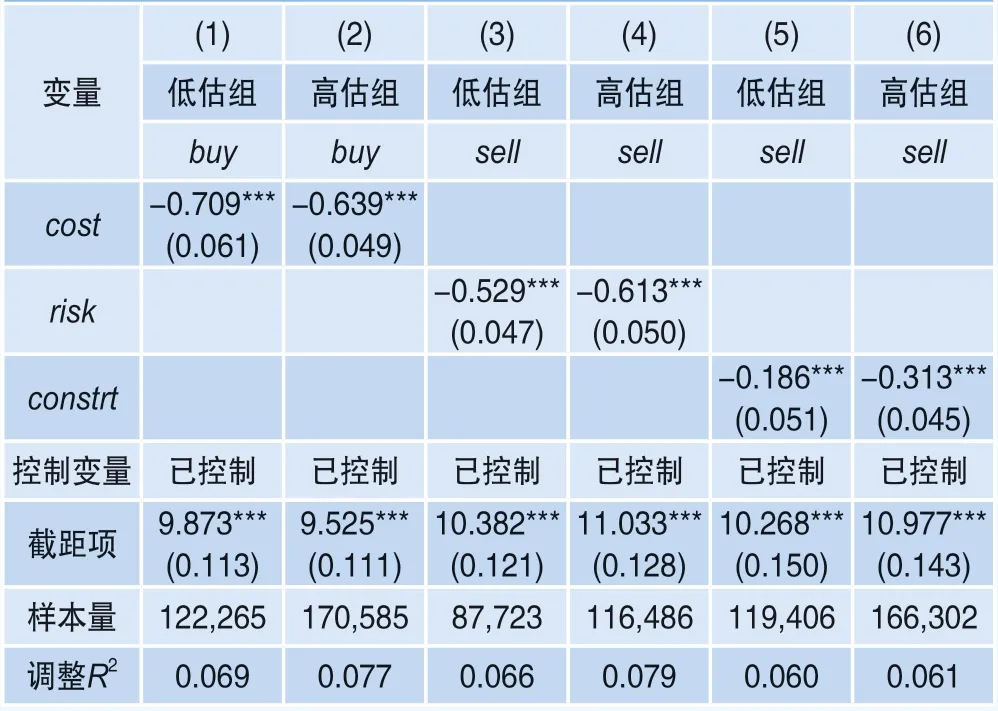
表9 不同估值情形下各类套利限制对主动买入(卖出)比率的影响
可以看出,无论高估组还是低估组,交易成本对主动买入比率均有显著为负的影响,交易风险和交易约束对主动卖出比率均有显著为负的影响。这与表8的分组结果高度一致,证明了结论的稳健性。
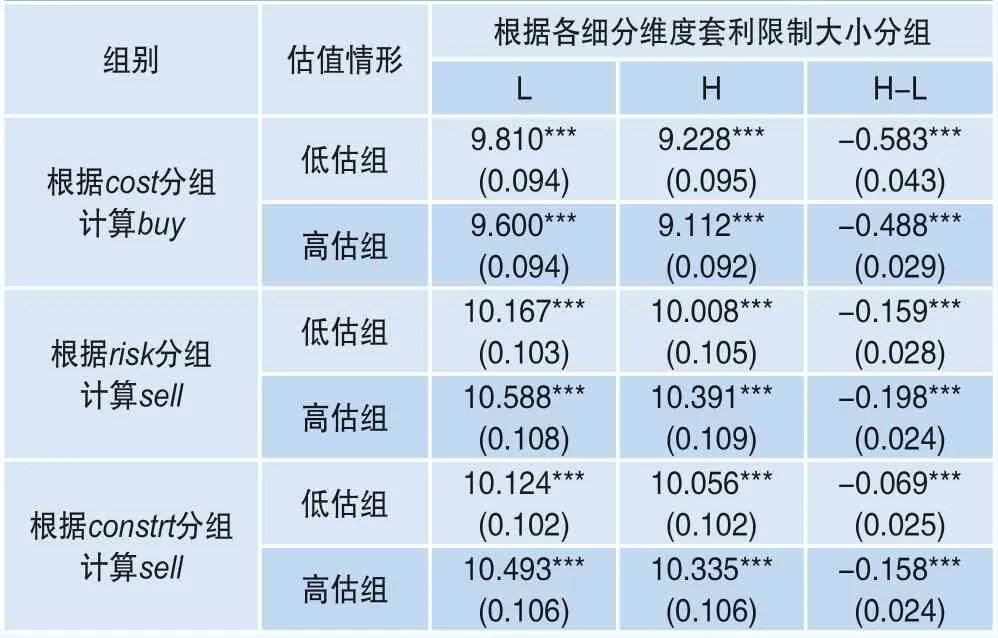
表8 不同估值情形下根据各细分维度套利限制分组的主动买入(卖出)比率
因此,上述分析结果印证了各细分维度套利限制通过改变投资者买卖行为,最终在不同估值情形下对错误定价产生异质性影响。交易成本在低估情形下加剧了错误定价,交易风险和交易约束在高估情形下加剧了错误定价,反之则反是。
五、结论与建议
本文使用2010―2020年A股市场相关数据构造了交易成本、交易风险和交易约束三类细分维度套利限制指标,研究套利限制对股票错误定价的影响。根据实证分析结果,得出以下结论:第一,各类套利限制越大,错误定价越严重。在影响错误定价的各细分维度套利限制中,交易约束起主导作用,交易成本次之,交易风险的影响则相对有限。第二,不同估值情形下,各类套利限制对错误定价的影响具有显著的差异性。低估情形下,交易成本在各细分维度套利限制中起主导作用,交易风险和交易约束并非导致错误定价的原因;高估情形下,在对错误定价具有正向影响的细分维度套利限制中,交易约束起主导作用,交易风险次之,交易成本并不是导致错误定价的原因。这一独特现象是由各细分维度套利限制对投资者买卖行为产生了不同影响导致的。第三,不同投资者情绪下各类套利限制对错误定价的影响无显著性差异,这说明套利限制对错误定价的影响不受投资者情绪的干扰,其影响独立且稳定。
根据以上结论,本文提出如下建议,以期为套利活动和我国资本市场基础制度改革提供参考:
第一,套利者应充分认识A股市场存在的各细分维度套利限制,要区别应对不同估值的股票,避免不必要的损失。在股票高估时,交易风险和交易约束是造成错误定价的重要原因,非理性投资行为以及不完善的卖空机制容易使套利者遭受损失,套利者在做空股票时要格外注意交易风险和交易约束对套利活动的影响。在股票低估时,交易成本是造成错误定价的原因,套利者需要充分考虑交易成本以获取超额收益。此外,套利者在进行跨境套利时,除考虑估值问题外,也要区分不同股票市场在各维度套利限制上的区别,避免套利损失。
第二,牛市阶段和熊市阶段监管部门提高市场定价效率的方式应有所差异。在牛市阶段可降低交易风险和交易约束,以降低交易约束为主要手段。可以通过加强上市公司信息披露、增加机构投资者比例等方式降低交易风险,通过扩大融资融券标的范围、放宽涨跌幅限制以及改T+1交易制度为T+0等方式减少交易约束。在熊市阶段可以降低交易成本为主要手段,通过减税降费、增强股票市场流动性等方式提振股票市场,减少错误定价,提高定价效率。

