面向SD-DCN 的OpenFlow 分组转发能效联合优化模型
罗 可 曾 鹏 熊 兵 赵锦元
1(长沙理工大学计算机与通信工程学院 长沙 410114)
2(长沙师范学院信息科学与工程学院 长沙 410199)
软件定义网络(software-defined networking,SDN)作为一种新兴网络架构,将网络控制功能从数据交换设备中解耦出来,形成逻辑上集中的控制平面.SDN 控制平面负责构建并维护全局网络视图,根据网络拓扑结构制定流规则,并通过以OpenFlow 为代表的南向接口协议下发到数据交换设备中,从而实现灵活高效的数据传输.基于OpenFlow 的SDN 技术有力地打破了传统网络的封闭和僵化问题,大大提升了网络的灵活性、可管控性和可编程能力,被普遍认为是未来网络最有发展前景的方向之一[1-2].经过十来年的不断发展与演进,SDN 技术已广泛应用于各种网络场景,尤其是数据中心网络.软件定义数据中心网络(software-defined data center network,SDDCN)显著简化了网络功能管理,降低了部署成本,提高了数据传输效率,优化了网络应用性能,为数据中心的优化部署提供了新的技术方案[3-4].
数据中心作为承载海量数据处理的重要基础设施,广泛应用于在线购物、网络电视、短视频分享等数据密集型产业,目前已进入井喷式的高速建设和发展时期[5].然而,在数据中心规模飞速扩张的同时,能耗问题已成为制约其可持续发展的瓶颈.在数据中心能耗中,网络设备产生的能耗占比可达50%以上[6],主要由提供高速数据传输服务的交换机产生.在SD-DCN 网络中,OpenFlow 交换机通常采用三态内容可寻址存储器(ternary content addressable memory,TCAM)存储流表以支持快速通配查找,其查找能耗高(15~30 W/Mbit)[7-8],约为 静态存储器的50 倍[9].同时,SD-DCN 网络采用等价多路径路由机制,将产生不少额外的流规则并存储到TCAM 中,导致能耗问题更加凸显.因此,如何设置OpenFlow 交换机的TCAM容量,以平衡分组转发时延和TCAM 查找能耗,是SD-DCN 实际部署需要解决的一个关键问题.
目前已有不少研究工作关注OpenFlow 交换机的TCAM 能耗问题.为降低TCAM 查找能耗,部分研究人员采用内容可寻址存储器(CAM)缓存流表中的活跃流[10-11],进而直接转发大多数分组,以大幅度减少TCAM 流表查找操作.然而,CAM 同样采用并行查找方式,查找能耗仍高.也有研究者利用过滤器预测流表查找失败情形[9],减少不必要的TCAM 查找操作,但只能过滤每条流的首个分组,节能效果极为有限.还有研究人员关注OpenFlow 交换机的TCAM 流表优化模型[12-13],但却主要关注流超时设置、流规则放置等问题,缺乏对其最优容量的考量.此外,许多工作关注OpenFlow 交换机的分组转发时延,利用排队论构建OpenFlow 分组转发性能模型[14-15],但却同样忽略了TCAM 容量对分组转发时延的影响.
针对上述问题,本文面向SD-DCN 网络场景,拟提出一种OpenFlow 分组转发能效联合优化模型,以求解TCAM 最优容量.为此,本文首先描述了一个典型的SD-DCN 网络部署场景,分析其分组转发过程和排队特性,构建OpenFlow 分组转发时延模型.然后,根据数据中心网络中的流分布特性,建立TCAM 命中率模型,进而求解OpenFlow 分组转发时延与TCAM容量的关系式.进一步,结合TCAM 查找能耗,建立OpenFlow 分组转发能效联合优化模型,并设计对应的优化算法求解TCAM 最优容量.最后,通过模拟实验评估本文所提OpenFlow 分组转发时延模型,并利用优化算法求解不同参数配置下的TCAM 最优容量.
本文的主要贡献有4 个方面:
1)针对SD-DCN 网络典型部署场景,在分析其分组到达和处理过程的基础上,为OpenFlow 交换机构建了多优先级M/G/1 排队模型,进而建立了一种更准确的OpenFlow 分组转发时延模型;
2)基于SD-DCN 网络中的流量分布特性,为OpenFlow 交换机建立了TCAM 命中率模型,以求解OpenFlow 分组转发时延与TCAM 容量的关系式;
3)以分组转发时延和能耗为优化目标,建立OpenFlow 分组转发能效联合优化模型;
4)证明了优化目标函数的凸性质,进而设计了优化算法求解TCAM 最优容量,为SD-DCN 实际部署提供有效指导.
1 相关工作
针对OpenFlow 交换机的TCAM 能耗问题,部分研究人员设计了TCAM 流表节能查找方案.Congdon等人[10]根据网络流量局部性,为交换机的每个端口设置CAM 缓存,存储包签名与流关键字之间的映射关系,以预测包分类结果,使大部分分组绕过TCAM查找过程.然而,CAM 存储器同样采用并行查找方式,查找能耗仍高.针对OpenFlow 多流表的流水线查找模式,Wang 等人[11]利用马尔可夫模型选取每个流表中的活跃表项,并集中存放到流水线前的Pop 表中,使大部分分组查找命中Pop 表,以避免复杂的多流表查找过程.Kao 等人[9]提出了基于布鲁姆过滤器的流表查找方案TSA-BF,通过优化设计布鲁姆过滤器以预测流表查找失败情形,使新流分组绕过TCAM失败查找操作.但该方案只能过滤每条流的首个分组,节能效果极为有限.
同时,许多研究工作利用排队论建立OpenFlow分组转发时延模型.针对OpenFlow 交换机的分组处理过程和SDN 控制器的Packet-in 消息处理过程,Xiong等人[14]将其分别建模为MX/M/1 和M/G/1 排队模型,Abbou 等人[15]则分别建模成M/H2/1 排队模型和M/M/1排队模型,Chilwan 和Jiang[16]分别建模成M/M/1/∞和M/M/1/K 排队模型,进而推导OpenFlow 平均分组转发时延.针对多控制器部署场景,Zhao 等人[17]为SDN控制器集群和OpenFlow 交换机分别建立M/M/n 和M/G/1 排队模型,分析平均分组转发时延,并结合SDN控制器集群的部署成本,求解最优控制器数量.然而,文献[14-17]所述模型未考虑不同类型网络分组的优先级差异.对此,Rahouti 等人[18]将SDN 网络建模成带反馈机制的双队列排队系统,将分组划分成多个优先级队列,以提供差异化的QoS 服务.Li 等人[19]为OpenFlow 虚拟交换机的分组转发过程建立排队系统,以分析丢包率、流表查找失败概率、分组转发时延等关键性能指标,进而利用多线程处理、优先制队列设置、分组调度策略和内部缓存区设置等多种方法优化分组转发性能.然而,文献[18-19]所述模型均未考虑TCAM 容量对OpenFlow 分组转发时延的影响.
进一步,已有部分研究工作关注OpenFlow 交换机的TCAM 流表优化模型.Metter 等人[20-21]建立基于M/M/∞排队系统的流表解析模型,分析不同网络流量特性下流超时时长对Packet-in 发送消息速率和流表占用率的影响.进一步,AlGhadhban 等人[12]为流安装过程建立基于类生灭过程的解析模型,分析流表匹配概率的影响因素,进而推导不同流超时时长下的流表容量.Zhang 等人[13]采用M/G/c/c 排队系统分析流超时时长对流规则的截断时间、冗余时间和安装失败率的影响,进而提出自适应流超时算法,以提高TCAM 流表资源利用率.然而,文献[12-13,20-21]所述模型未考虑TCAM 容量优化设置问题.对此,Shen等人[22]将流表项生命周期划分为Packet-in 消息发送、控制器处理和流表项超时3 个阶段,并分别建立M/M/1,M/M/1 和M/G/c/c 排队模型,进而提出流表空间估计模型,求解流安装失败概率约束下的TCAM最小容量.然而,该工作仅关注TCAM 容量对流安装成功率的影响,却没有考虑流表命中率和分组转发时延等关键性能指标.本文则考虑TCAM 容量对分组转发时延和能耗的影响,建立OpenFlow 分组转发能效联合优化模型,求解TCAM 最优容量,为SDDCN 实际部署提供参考依据.
2 面向SD-DCN 的OpenFlow 分组转发时延模型
本节在描述SD-DCN 网络典型部署场景的基础上,为OpenFlow 交换机的分组处理过程构建多优先级M/G/1 排队模型,进而建立OpenFlow 分组转发时延模型.
2.1 SD-DCN
随着在线购物、网络电视、视频分享、搜索引擎等数据密集型应用的日益盛行,数据中心作为承载海量数据处理的重要基础设施,其规模不断扩大,网络通信量正快速增长[23].传统数据中心网络因扩展性差、缺乏灵活的管理,无法满足数据处理业务中日益增长的网络需求.基于OpenFlow 的SDN 技术将控制逻辑与数据转发相解耦,进而对网络设备进行逻辑上集中的管理和控制,并为上层应用提供统一的编程接口,大大提升了网络的灵活性、开放性和可管控能力,为构建高性能数据中心网络提供了新的解决思路.SD-DCN 具备动态路由控制、服务质量管理、安全智能连接等技术优势,降低了数据中心网络的部署成本,有助于构建更加灵活高效的数据中心,已成为一种新的发展趋势[24].
图1 描述了一种典型的SD-DCN 网络架构,分为基础设施平面、数据平面、控制平面和应用平面.基础设施平面包含众多服务器,提供强大的存储和计算能力.数据平面大多采用fat-tree 拓扑结构组网[25-26],交换机自下而上分为边缘交换机、汇聚交换机和核心交换机,为众多服务器提供高性能的网络互联和数据传输服务.在数据平面中,每个交换机根据控制平面下发的流规则,快速转发网络分组.控制平面根据上层应用需求,基于全局网络视图制定流规则,并通过以OpenFlow 为代表的南向接口协议下发到各个交换机中,指导分组转发行为.应用平面基于控制平面提供的北向接口,实现服务编排、安全控制、QoS管理、资源调度等功能.
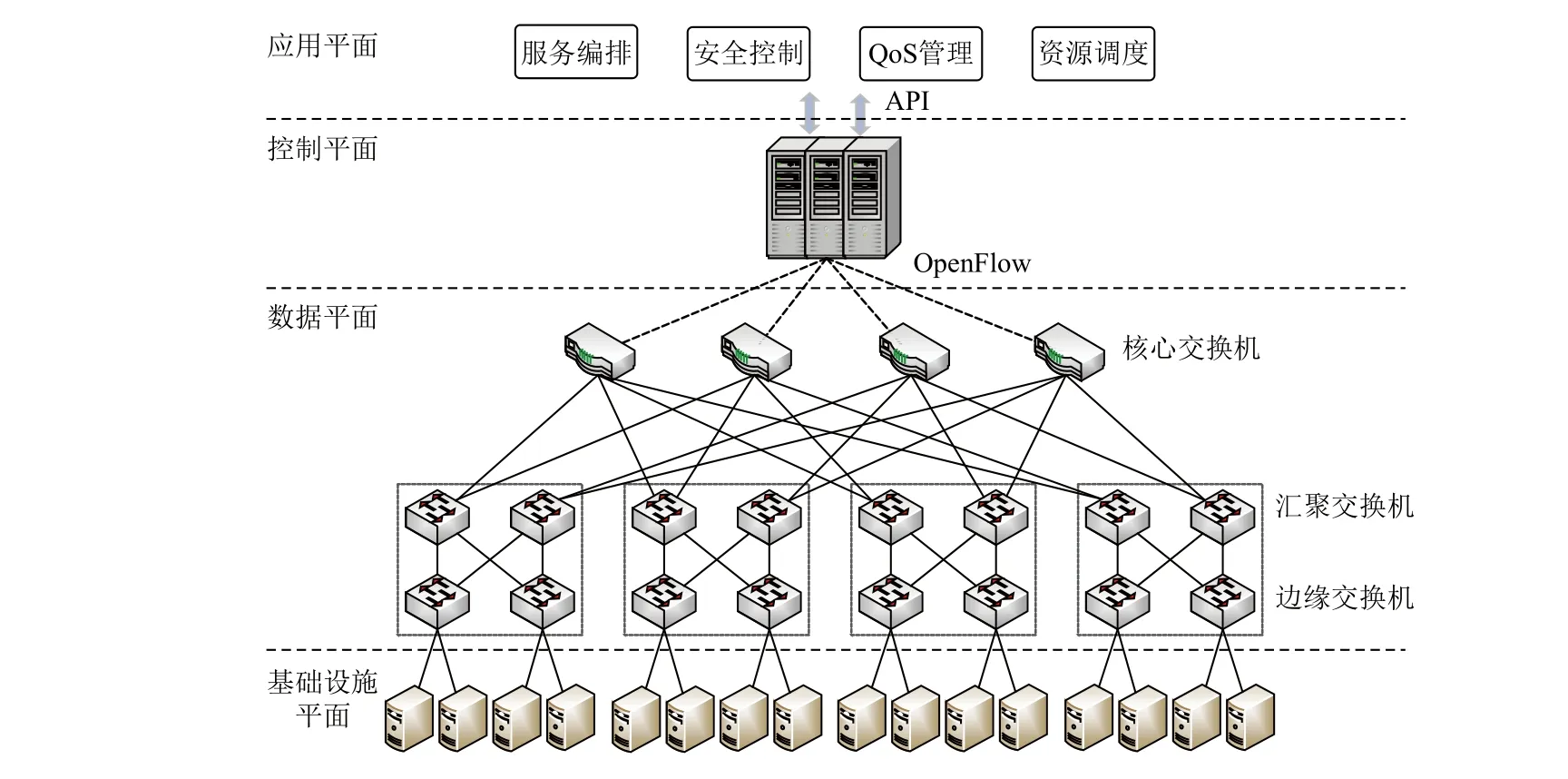
Fig.1 Network architecture of SD-DCN图1 SD-DCN 网络架构
在图1 所示的SD-DCN 网络场景中,OpenFlow交换机根据SDN 控制器制定的流规则转发分组.对于每个到达的分组,交换机从分组首部提取匹配字段,进而查找流表.若查找成功,则依据流表项中给定的动作集转发分组.否则,交换机判定该分组属于新流,将其首部信息或整个分组封装成流安装请求发送到控制器.控制器根据全局网络视图生成流规则,并下发到流传输路径上的各个交换机中.交换机将流规则安装至流表,并据此转发该流后续到达的分组.
2.2 OpenFlow 交换机排队模型
在SD-DCN 数据平面中,来自服务器的大量分组汇聚到OpenFlow 交换机,形成队列等待处理.OpenFlow交换机的分组排队和处理过程如图2 所示.对于到达的每个分组,交换机首先将其缓存到入端口队列,然后逐个解析分组首部信息,提取关键字段,以计算流标识符.再根据流标识符查找OpenFlow 流表,以定位对应的流表项.若查找成功,交换机在ACL 应用、计数器更新等一系列相互独立的操作后,将分组发送到出端口等待转发;若查找失败,交换机发送Packetin 消息给控制器,待收到相应的Flow-mod 消息后,将其中的流规则安装到TCAM 流表,并据此转发该流后续到达的分组.控制器下发的Flow-mod 消息同样以分组的形式到达交换机,但优先级高于数据分组,以保证分组转发行为的一致性和高效性.
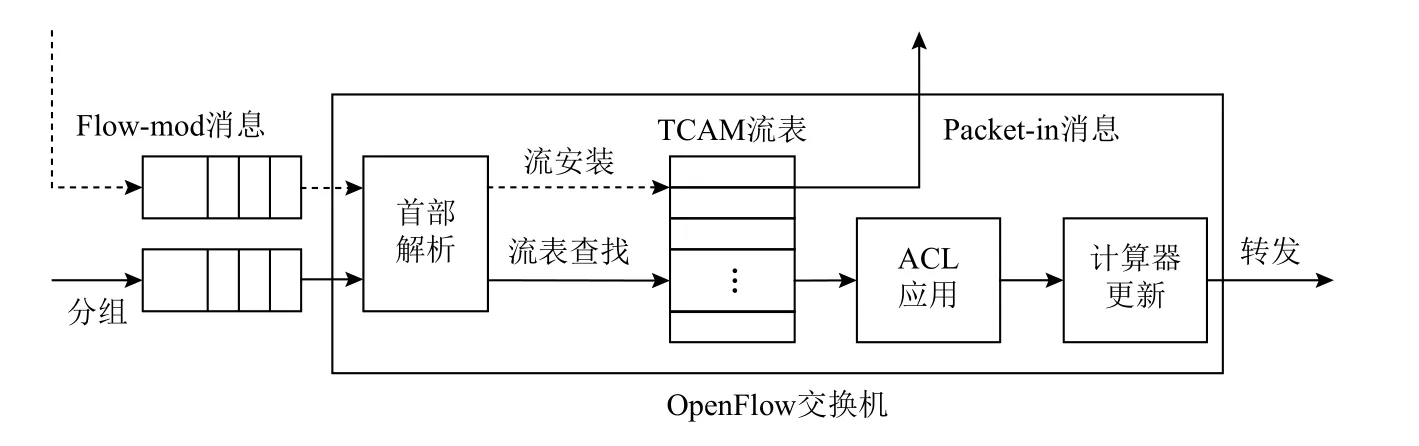
Fig.2 The queueing and processing of packet in the OpenFlow switch图2 OpenFlow 交换机的分组排队和处理过程
网络测量结果表明:在数据中心等大规模网络场景下,流量汇聚程度高,并发流数量庞大,趋于相互独立[27-28].因此,OpenFlow 交换机的分组到达过程和流到达过程均可视为泊松过程[17,22].在Open-Flow 分组转发过程中,所有新流的首个分组在Open-Flow 交换机中的处理步骤相同,且处理过程相互独立.根据Burke 定理[29],交换机发送的Packet-in 消息流仍为泊松流.假设每台交换机发送的Packet-in 消息流相互独立,根据泊松流的可加性,汇聚到控制器的Packet-in 消息流可叠加为泊松流.控制器为每个Packet-in 消息独立生成流规则后,以Flow-mod 消息的形式下发至流路径上的各个交换机.因此,Open-Flow 交换机的Flow-mod 消息到达过程同样为泊松过程.假定控制器收到交换机Sk发送的Packet-in 消息后,生成流规则并下发Flow-mod 消息给交换机Si的概率为δik,则有δii=1.若交换机Sk的Packet-in 消息发送速率为 λ(in),控制器共管理K台交换机,则交换机Si的Flow-mod 消息到达速率如式(1)所示:
OpenFlow 交换机的分组处理过程可分解为首部解析、流表查找、计数器更新等相互独立的步骤,不妨假设其共有M步.假设交换机Si中第j(1≤j≤M)步的处理时间Tij服从速率为μij的负指数分布,则其均值E(Tij)=1/μij,方差D(Tij)=1/.由于每个步骤相互独立,因此交换机Si的分组处理时间Ti服从一般分布,其均值E(Ti)如式(2)所示:
因此,交换机Si的平均分组处理速率和分组处理时间方差分别如式(3)(4)所示:
基于以上排队分析,本文将OpenFlow 交换机的分组处理过程建模为多优先级M/G/1 排队模型:1)交换机Si的Flow-mod 消息和分组到达过程为泊松过程,到达速率分别为;2)OpenFlow 交换机的入端口有Flow-mod 消息高优先级队列和分组低优先级队列,按非抢占式多优先级调度策略依次处理;3)交换机Si的分组处理时间服从一般分布,分组处理速率和分组处理时间方差,分别如式(3)(4)所示.根据排队论,可计算出Flow-mod 消息和分组在交换机中的平均逗留时间为,分别如式(5)(6)所示:
2.3 OpenFlow 分组转发时延模型

Fig.3 OpenFlow-based packet forwarding queueing system图3 OpenFlow 分组转发排队系统
在上述OpenFlow 分组转发排队系统中,到达控制器的Packet-in 消息流相互独立,其到达过程为泊松过程,且控制器对每个Packet-in 消息的处理过程相互独立,处理时间可视为服从负指数分布[30-31].因此,可将控制器的Packet-in 消息处理过程建模为M/M/1 排队模型,进而可知Packet-in 消息在控制器中的平均逗留时间W(c)如式(8)所示:
根据上述OpenFlow 交换机的分组处理排队模型和控制器的Packet-in 消息处理排队模型,可推导出交换机Si的平均分组转发时延.根据OpenFlow 分组转发过程可知,交换机Si中的分组转发过程可分为2 种情况:直接转发和请求控制器安装流规则的间接转发.分组直接转发时延即为分组在交换机中的逗留时间.分组间接转发时延包含分组在交换机中的逗留时间、Packet-in 消息在控制器中的逗留时间W(c)、Flow-mod 消息在 交换机 中的逗 留时间,以及Packet-in 消息和Flow-mod 消息在交换机到控制器之间的总传输时延.因此,交换机Si的平均分组转发时延可表达如式(9)所示:
将式(5)(6)(8)代入式(9)可得,交换机Si的平均分组转发时延Di如式(10)所示:
3 面向SD-DCN 的OpenFlow 分组转发能效联合优化模型
本节根据SD-DCN 中的网络流分布特性建立TCAM 命中率模型,进而结 合 2.3 节所述 的OpenFlow 分组转发时延模型,建立OpenFlow 分组转发能效联合优化模型,以求解TCAM 最优容量.
3.1 TCAM 命中率模型
在分组交换网络中,网络流量存在明显的局部性特点,大部分分组集中分布在少数流中[32].以数据中心网络为例,众多测量研究结果表明:20%的top流占据分组总数的80%以上[33].根据网络流量局部性,众多研究利用Zipf 分布刻画网络流中的分组数量分布特性[34-37].假设网络中有N条流,则可按照流大小即流的分组数量依次递减排序为(f1,f2,…,fN).根据Zipf 分布可知,流fr的分组数量Q(r)与其大小排名r(r=1,2,…,N)存在式(11)所示的幂律关系.
其中C和α均为大于0 的常数,α表示分组在网络流中分布的倾斜程度.假设OpenFlow 交换机的TCAM容量为n条流表项,且存储所有网络流中排名靠前的n条流,则TCAM 命中率h(n)如式(12)所示:
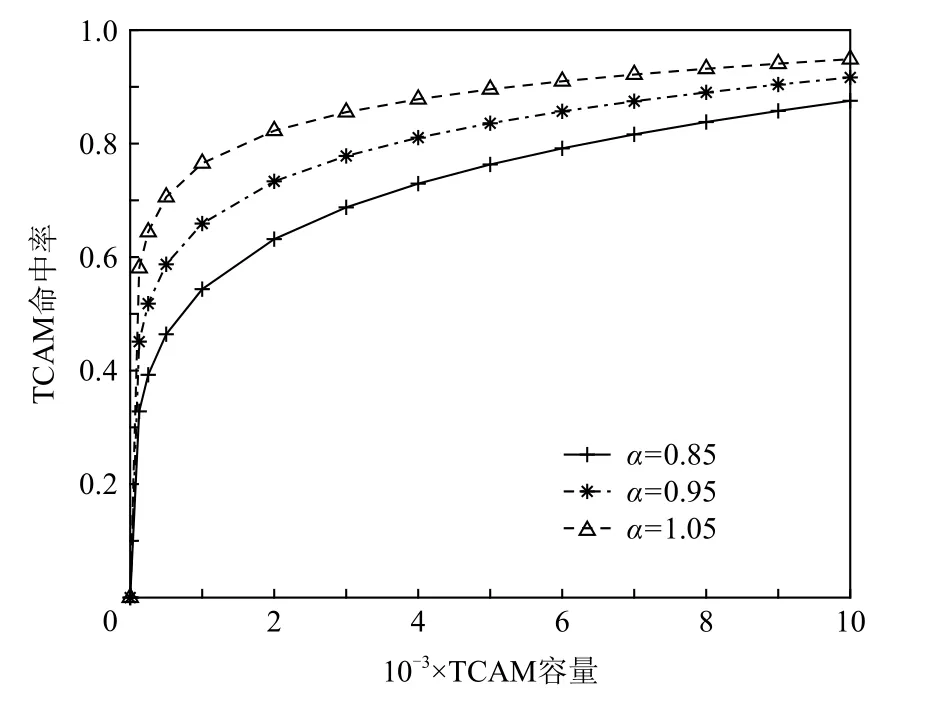
Fig.4 Estimated relationship between TCAM hit rate and TCAM capacity图4 TCAM 命中率与TCAM 容量的估计关系
从图4 中可看出:α越大,相同容量下的TCAM命中率越高,即相同数量top 流所占据的分组比例越高,网络流量局部性越明显.当TCAM 容量为4 000条流表项,即可存储前20%的流时,若α=0.95,则TCAM 命中率可达81.05%,与数据中心网络中的流量测量结果基本一致.
3.2 OpenFlow 分组转发能效联合优化模型
在OpenFlow 分组转发过程中,每个到达交换机的分组都需要查找TCAM 流表,进而实现分组转发处理.根据2.3 节所述的OpenFlow 分组转发时延模型和3.1 节所述的TCAM 命中率模型可知:TCAM 容量越大,存储的流规则越多,TCAM 命中率越高,即TCAM 流表查找成功的分组占比越大,平均分组转发时延越小.因此,平均分组转发时延与TCAM 容量呈负相关关系.由于TCAM 采用并行匹配方式查找整个流表,查找能耗基本上与其容量成正比,假定分组转发过程中的其他能耗固定,则分组转发能耗可视为与TCAM 容量呈正线性相关关系.因此,可将TCAM 容量作为决策变量,以分组转发时延和能耗为优化目标,建立能效联合优化模型求解TCAM 最优容量.
对于TCAM 容量为n的OpenFlow 交换机,根据式(12)所示的TCAM 命中率,定义TCAM 流表命中失败概率q(n)=1-h(n).进而结合式(10),可求出交换机的平均分组转发时延D(n):
同时,根据式(12)给出的TCAM 命中率,可建立OpenFlow 交换机的分组转发能耗模型.假定每条TCAM 流表项的平均查找能耗为e1,由于TCAM 容量为n条流表项,且采用并行查找方式,因此每个分组的TCAM 查找能耗为ne1.若分组转发过程中的其他处理能耗为e0,则交换机的平均分组转发能耗E(n)如式(15)所示:
以式(13)和式(15)分别给出的平均分组转发时延和能耗为优化目标,可建立式(16)所示的Open-Flow 分组转发能效联合优化模型,求解TCAM 最优容量.
其中约束条件为
式(16)优化模型包含3 个约束条件:1)平均分组转发时延D(n)不能超过QoS 规定的最大时延Dmax;2)平均分组转发能耗E(n)不能超过上限值Emax;3)TCAM 容量n为正整数.
3.3 优化模型求解
OpenFlow 分组转发能效联合优化模型是一个不等式约束下的多目标优化模型.在该模型中,以TCAM 容量n为决策变量,平均分组转发时延D(n)可通过定理1 证明具有单调递减性,平均分组转发能耗E(n)显然单调递增.而约束条件限定了D(n)和E(n)的最大值,即决定了TCAM 容量的最小值nmin和最大值nmax,进而可求得D(n)和E(n)的最小值分别为Dmin=D(nmax)和Emin=E(nmin).
定理1.对于式(13)中的平均分组转发时延D(n),若其参 数均为 正,且ρ(m)+ρ(p)=ρ(s)<1,ρ(c)=λ(c)/μ(c)<1,则D(n)具有单调递减性,即D′(n)<0.
证明.对于式(13),不妨假设n为连续自变量,利用复合函数求导法,可得D(n)的一阶导数:
进而可知1-a1q(n)>0.由于ρ(m)+ρ(p)=ρ(s)<1,则有1-a1q(n)-ρ(p)=1-ρ(s)>0.带入式(20)(21)中可得
加之各项参数为正,因此式(19)等号右边的每项均为正,进而可得D′(q(n))>0.对q(n)求导有
将上述结论带入式(18)可知:D′(n)<0.
证毕.
此时,可将优化目标D(n)和E(n)分别进行归一化处理,进而利用线性加权法将式(16)中的多目标优化函数转换成单目标优化函数f(n):
其中ω为OpenFlow 平均分组转发时延所占的权重.该函数具有凸性质,如定理2 所证.
定理2.对于式(27)所示的目标函数,若其参数均为正,且ρ(s)<1,ρ(c)<1,则该函数具有凸性质,即f′′(n)>0.
证明.对f(n)二阶求导有
其中g(q(n))和g′(q(n))分别如式(20)和式(21)所示.根据定理1 的证明过程可知
根据定理1 的证明 过程可 知1-a1q(n)>0,μ(c)-a0q(n)>0,g(q(n))>0,g'(q(n))<0.加之各项参数均为正,则式(29)等号右边的每项均为正,进而可知D′′(q(n))>0.同时,根据定理1 的证明过程可知D′(q(n))>0.代入式(28)可得f′′(n)>0.
证毕.
由于目标函数f(n)具有凸性质,因此可利用二分法在整数范围[nmin,nmax]内搜索TCAM 最优容量nopt,使f(n)取最小值.算法1 给出了OpenFlow 分组转发能效联合优化模型的求解算法.
算法1.OpenFlow 分组转发能效联合优化算法.
输入:1)网络拓扑信息G(V,E);2)OpenFlow 交换机的分组到达速率λ(p),每个步骤j的处理速率,控制器的Packet-in 处理速率μ(c);3)平均每条TCAM 流表项的查找能耗e1,分组转发过程中其他处理步骤的能耗之和e0,分组转发能耗上限Emax;4)QoS 允许的分组转发时延上限Dmax.
输出:交换机的TCAM 最优容量nopt.
算法1 分为3 个步骤:1)计算中间参数,包括交换机处理速率μ(s)(行①),交换机Sk发送的Packet-in消息触发控制器下发Flow-mod 消息到交换机Si的概率δik(行②);2)确定TCAM 容量n的整数范围[nmin,nmax](行⑥⑦);3)二分查找TCAM 容量的最优值nopt(行⑧~⑰).
4 实 验
本节首先通过模拟实验评估本文所提OpenFlow分组转发时延模型的准确性,然后采用数值分析方法分析不同因素对分组转发时延的影响,进而求解不同参数下的TCAM 最优容量.
4.1 时延模型对比
实验采用Mininet 平台模拟典型的Fat-tree 网络拓扑结构[22],SDN 控制器共管理10 台OpenFlow 交换机,包含2 台核心交换机、4 台汇聚交换机、4 台边缘交换机.其中,SDN 控制器采用OpenDaylight,Open-Flow 交换机采用Open vSwitch v2.13.在模拟实验中,利用OFsuite 性能测试工具测得控制器的Packet-in 消息处理速率为21 kmsg/s,每台交换机的分组处理速率为20 kpkt/s.同时,将交换机的流表容量设置为8 000条流表项,流超时间隔为10 s.实验利用Iperf 工具为每台交换机模拟产生不同速率的网络流量,其中新流分组占比约为10%,进而测得平均分组转发时延如图5 所示.同时,将上述参数代入本文所提的Open-Flow 分组转发时延模型和现有模型,其中控制器均采用M/M/1 模型,OpenFlow 交换机分别采用多优先级M/G/1 模型、M/G/1 模型[17]、Mk/M/1 模型[14],进而计算出平均分组转发时延的估计值如图5 所示.
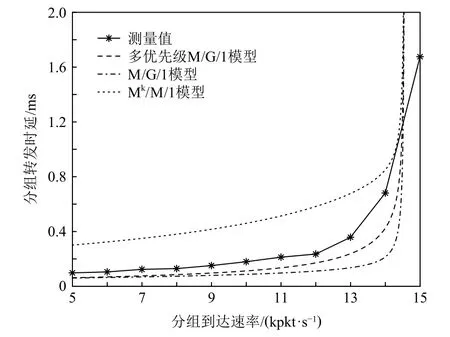
Fig.5 Comparison of delay models with different packet arrival rates图5 不同分组到达速率下的时延模型对比
从图5 中可以看出:与现有模型相比,本文所提基于多优先级M/G/1 的OpenFlow 分组转发时延模型具有更接近于测量值的估计时延.OpenFlow 交换机的分组处理过程包含多个相互独立的步骤,而Mk/M/1 模型将分组处理时间简单地看作服从泊松分布,故其估计时延与测量值相差较大.M/G/1 模型可较为准确地估计OpenFlow 交换机的分组处理时间,但在分组到达速率较大时,其估计时延明显较小.这是因为该模型只考虑到达OpenFlow 交换机的数据分组,而忽略了控制器下发的消息分组.多优先级M/G/1 模型则着重考虑了Flow-mod 消息的分组处理时延,因而其分组转发时延估计值更接近于测量值.
实验采用4.1 节所述参数,将OpenFlow 交换机的分组到达速率设为10 kpkt/s,并不断调整OpenFlow 交换机的流表容量值,可测得平均分组转发时延如图6所示.同时,将上述参数代入本文所提的OpenFlow 分组转发时延模型和现有模型,计算出平均分组转发时延的估计值如图6 所示.

Fig.6 Comparison of delay models with different flow table capacities图6 不同流表容量下的时延模型对比
从图6 中可以看出:本文所提OpenFlow 分组转发时延模型的估计时延比现有模型更接近于测量时延.现有模型由于忽略了流表容量对分组转发时延的影响,其分组转发时延始终保持不变,估计不准确.与此形成对照的是,随着流表容量的不断增大,本文所提模型的分组转发时延估计值逐步降低,并趋于稳定,与测量值接近.这是因为交换机的流表命中率随流表容量的增大而升高,进而导致发送给控制器的Packet-in 消息逐渐减少,其估计时延逐步接近于M/G/1 模型.特别地,当交换机的流表容量小于3 000条流表项时,模拟实验中的控制器负载过大,将会丢弃部分Packet-in 消息,导致分组转发时延测量值急剧升高.此时,对于OpenFlow 分组转发时延模型,由于流表命中率过低,控制器的Packet-in 消息到达速率高于其处理速率,导致模型失效.
4.2 分组转发时延
进一步,实验采用数值分析方法研究平均分组转发时延的主要影响因素.实验参数设定为:假定分组在网络流中的分布倾斜程度α=0.95,每台OpenFlow 交换机的分组到达速率λ(p)=10 kpkt/s,分组处理过程分为10 个步骤,且每个步骤的处理速率相同,分组处理速率μ(s)=20 kpkt/s.同时,SDN 控制器的Packet-in 消息处理速率μ(c)=21 kmsg/s,每台控制器管理10 台OpenFlow 交换机.
实验设置不同的TCAM 容量,可得到平均分组转发时延与分组到达速率之间的关系如图7 所示.从图7 可看出:当TCAM 容量一定时,分组到达速率越高,交换机和控制器的负载越大,平均分组转发时延越高.同时,当分组到达速率一定时,交换机的TCAM容量越大,流表命中率越高,Packet-in 消息的发送速率越低,其在控制器中的逗留时间越短,平均分组转发时延越低.此外,TCAM 容量越大,允许的分组到达速率越高.具体而言,当交换机的TCAM 容量n分别为4 000,6 000,8 000,10 000 条流表项时,平均分组转发时延在分组到达速率λ(p)分别超过10 kpkt/s,11.6 kpkt/s,12.8 kpkt/s,13.8 kpkt/s 时急剧上升,且允许的最大分组到达速率分别为10.7 kpkt/s,12.6 kpkt/s,14.3 kpkt/s,15.3 kpkt/s.
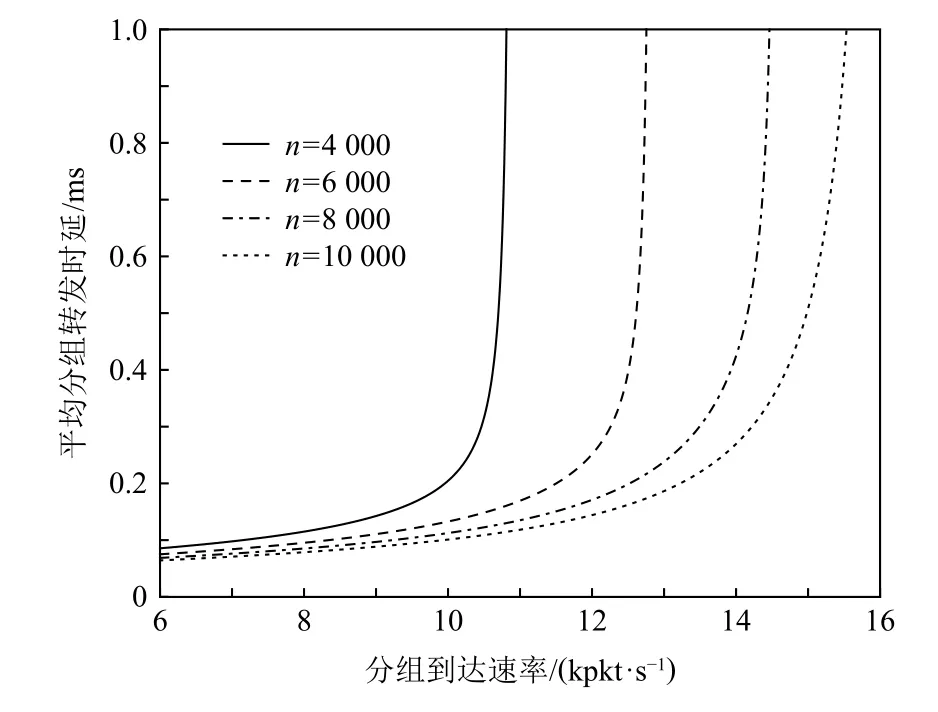
Fig.7 Relationship between average packet forwarding delay and packet arrival rate图7 平均分组转发时延与分组到达速率的关系
实验设置不同的TCAM 容量,可得到平均分组转发时延与分组处理速率之间的关系,如图8 所示.从图8 可看出:当TCAM 容量一定时,分组处理速率越高,分组在交换机中的逗留时间越短,平均分组转发时延越低;同时,当分组处理速率一定时,交换机的TCAM 容量越大,流表命中率越高,发送给控制器的Packet-in 消息越少,相应收到的Flow-mod 消息也越少,平均分组转发时延越低.此外,TCAM 容量越大,交换机的分组处理速率需求越低.具体而言,当交换机的TCAM 容量n分别为4 000,6 000,8 000,10 000条流表项时,平均分组转发时延在分组处理速率μ(s)分别小于16 kpkt/s,14.5 kpkt/s,13.7 kpkt/s,13.2 kpkt/s时急剧上升,且交换机允许的最小分组处理速率分别为14.3 kpkt/s,13.4 kpkt/s,12.7 kpkt/s,12.1 kpkt/s.

Fig.8 Relationship between average packet forwarding delay and packet processing rate图8 平均分组转发时延与分组处理速率的关系
实验设置不同的TCAM 容量,可得到平均分组转发时延与Packet-in 消息处理速率之间的关系如图9 所示.从图9 中可看出:当TCAM 容量一定时,Packet-in 消息处理速率越高,其在控制器中的逗留时间越短,平均分组转发时延越低.同时,当Packet-in消息处理速率一定时,交换机的TCAM 容量越大,流表容量越高,Packet-in 消息的发送速率越小,其在控制器中的逗留时间越短,平均分组转发时延越低.此外,交换机的TCAM 容量越大,控制器允许的Packet-in消息处理速率越低.具体而言,当交换机的TCAM 容量n分别为4 000,6 000,8 000,10 000 条流表项时,平均分组转发时延在Packet-in 消息处理速率μ(c)分别低于18 kmsg/s,15 kmsg/s,12 kmsg/s,8 kmsg/s 时急剧上升,且控制器允许的最低Packet-in 消息处理速率分别为18.9 kmsg/s,14.1 kmsg/s,10.6 kmsg/s,7.9 kmsg/s.
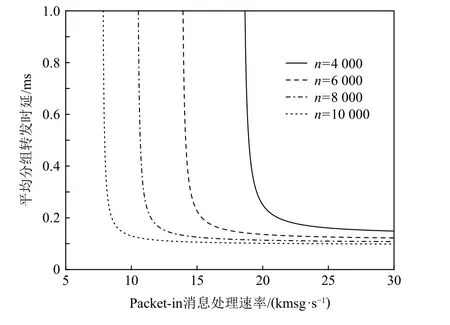
Fig.9 Relationship between average packet forwarding delay and Packet-in message processing rate图9 平均分组转发时延与Packet-in 消息处理速率的关系
4.3 TCAM 最优容量
对于OpenFlow 分组转发能效联合优化模型,不妨假设每条TCAM 流表项的平均查找能耗e1为1 个单位,其他处理步骤的能耗e0为3 000 个单位,分组转发能耗上限为Emax为15 000 个单位,即最大TCAM容量为12 000 条流表项.同时,QoS 要求的最大分组转发时延Dmax=1.5 ms.基于上述参数配置,将单目标优化函数f(n)中的权重ω设置不同值,进而实现OpenFlow 分组转发能效联合优化算法,求解不同分组到达速率下的TCAM 最优容量如图10 所示.
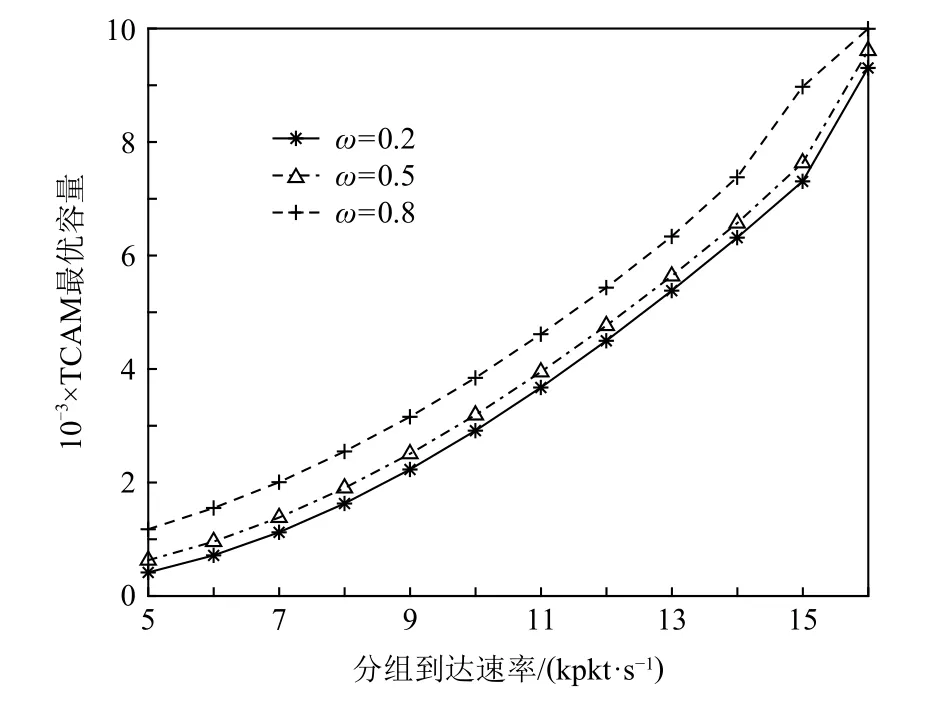
Fig.10 Optimal TCAM capacity with different packet arrival rates图10 不同分组到达速率下的TCAM 最优容量
从图10 中可看出:当每个交换机的分组到达速率增加时,TCAM 最优容量将随之增大,以提高TCAM命中率,保证Packet-in 消息发送速率不会过高,从而防止控制器过载,Packet-in 消息逗留时间过大.具体而言,当交换机的分组到达速率λ(p)分别为5 kpkt/s,10 kpkt/s,15 kpkt/s,且权重ω=0.8 时,TCAM 最优容量nopt分别为1 400,4 600,10 800 条流表项.当分组到达速率超过16 kpkt/s 时,交换机需要继续增大TCAM容量,以保证分组转发时延,但分组转发能耗将会超出上限,因而无解.此外,当分组到达速率一定时,分组转发时延的权重越高,TCAM 最优容量越大,以使TCAM 命中率越高,平均分组转发时延越小.
采用上述同样的参数配置,并将交换机的分组到达速率λ(p)设为10 kpkt/s,进而求解不同分组处理速率下的TCAM 最优容量,如图11 所示.从图11 中可看出:当交换机的分组处理速率升高时,TCAM 最优容量将随之减小,并趋于稳定.这是因为在保证分组转发时延的情况下,交换机的分组处理速率越高,需要的TCAM 容量越小.具体而言,当交换机的分组处理速率μ(s)分别为14 kpkt/s,16 kpkt/s,18 kpkt/s,且权重ω=0.8 时,TCAM 最优容 量nopt分别为8 900,5 800,4 900 条流表项.此外,当交换机的分组处理速率低于12 kpkt/s 时,由于逐步接近于分组到达速率,平均分组转发时延将超出QoS 规定的上限,因而无解.
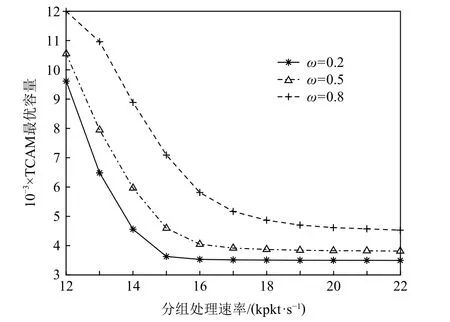
Fig.11 Optimal TCAM capacity with different packet processing rates图11 不同分组处理速率下的TCAM 最优容量

Fig.12 Optimal TCAM capacity with different Packet-in message processing rates图12 不同Packet-in 消息处理速率下的TCAM 最优容量
采用上述同样的参数配置,并将交换机的分组处理速率μ(s)设为20 kpkt/s,进而求解不同Packet-in消息处理速率下的TCAM 最优容量,如图12 所示.从图12 中可看出:当控制器的Packet-in 消息处理速率升高时,TCAM 最优容量将随之降低,并趋于稳定.这是因为控制器的Packet-in 消息处理速率越高,其允许的Packet-in 消息到达速率越高,进而交换机所需的TCAM 容量越少.具体而言,当Packet-in 消息处理速率μ(c)分别为15 kmsg/s,25 kmsg/s,35 kmsg/s,且权重ω=0.8 时,TCAM 最优容量nopt分别为6 600,3 800,2 900 条流表项.此外,当Packet-in 消息处理速率小于7 kmsg/s 时,交换机需要继续增加TCAM 容量,以提高TCAM 命中率,保证平均分组转发时延,但分组转发能耗将会超出上限,因而无解.
5 结论
本文针对SD-DCN 网络场景,利用多优先级M/G/1 排队模型刻画OpenFlow 交换机的分组处理过程,进而构建OpenFlow 分组转发时延模型.进一步,基于网络流分布特性建立TCAM 命中率模型,求解OpenFlow 分组转发时延与TCAM 容量的关系式.在此基础上,结合TCAM 查找能耗,建立OpenFlow 分组转发能效联合优化模型,以求解TCAM 最优容量.实验结果表明:与已有排队模型相比,本文所提时延模型更能准确估计SD-DCN 网络场景下的OpenFlow分组转发性能.同时,数值分析结果表明:交换机的TCAM 容量和控制器的Packet-in 消息处理速率对OpenFlow 分组转发时延有着关键性的影响,而交换机的分组到达速率和分组处理速率影响较弱.最后,通过OpenFlow 分组转发能效联合优化算法,求解出不同参数配置下的TCAM 最优容量,为SD-DCN 网络的实际部署提供参考依据.
作者贡献声明:罗可提出研究思路,并设计研究方案,以及修订论文最终版本;曾鹏完善论文创新点,并完成模型的建立和推导,以及撰写论文初稿主要部分;熊兵设计了实验思路,以及审查和修改润色论文;赵锦元协助创新点推导和论文修改;所有作者都参与了实验分析和手稿撰写.

