斜拉桥船撞风险分析

邓皓天，刘宪庆*，余葵，周强，唐亮

(1.重庆交通大学河海学院，重庆 400074； 2.国家内河航道整治工程技术研究中心，重庆 400074； 3.山区桥梁及隧道工程国家重点实验室，重庆 400074)

近年来，上海大治河桥、湖南平江大桥、上海斜塘大桥、广州洪奇沥大桥和珠海莲溪大桥相继遭受到不同船舶撞击，造成了不同程度的损失[1]。2021年1月，交通运输部印发《关于深化防范化解安全生产重大风险工作的意见》(交安监发〔2021〕2号)，给出《交通运输安全生产重大风险清单》，并将船舶碰撞桥梁风险列入交通运输领域安全生产重大风险清单中。因此，对桥梁结构进行船舶撞击风险评估尤为重要。

耿波[2]建立了一个桥船安全评估系统，并利用此系统对两座长江大桥进行安全评估。赵君黎等[3]将中国桥梁防撞规范与美国、欧洲等规范进行比较研究，发现差异较大。郑植等[4]对通明海特大桥桥墩在不同水位下的抗力水平进行分析，并对通明海特大桥的防护装置进行研究。张星星等[5]基于美国国家公路与运输协会(American Association of State Highway and Transportation Officials，AASHTO)模型，对桥间距、桥位以及能见度进行修正计算，并对典型桥型进行风险概率计算，结果表明风险概率评价较为合理。唐勇等[6]将AASHTO模型、KUNZI模型和改进的KUNZI模型进行比较分析，建议选用前两者的较大数值作为桥墩的碰撞概率。彭可可[7]对AASHTO模型进行改进，对双塔双索面斜拉桥船的动态偏航概率、年撞击频率进行计算。邵伟峰等[8]对AASHTO模型进行改进，提出动态桥梁碰撞概率，对白居寺长江大桥进行了船撞风险评估。付旭辉等[9]利用有限元法与AASHTO模型计算对比，对珠海淇澳大桥进行船撞能力评估。

现有的防撞设施有拱形自浮式水上升降防撞装置[10]、纤维增强复合材料(fiber reinforced polymer,FRP)防撞浮箱[11]、新型装配超高性能混凝土(ultra-high performance concrete，UHPC)防撞装置[12]、框架结构新型防撞装置[13]等防撞设施，但是加装防撞设施后仍存在较大风险，如2020年6月9日，西江大桥的防撞浮箱船舶侧向撞击后损毁，直接经济损失900万元，次生安全隐患明显。

目前对于大跨度斜拉桥船撞风险研究还不够完善[14]。斜拉桥是大跨度桥梁最主要的桥型，因此现以长江某斜拉桥为例，基于AASHTO模型对其涉水桥墩进行船撞风险分析，对自身抗撞能力、船舶撞击力以及桥梁年撞击概率和年撞损概率进行计算，确定桥梁船撞风险，并提出合理化建议。

1 工程概况

1.1 桥梁概况

算例桥为436 m双塔双索面斜拉桥。主桥桥长879 m，桥跨组合为主桥(35.5+186+436) m双塔斜拉桥，全桥长度1 198.94 m。该斜拉桥的整体布置图见图1。

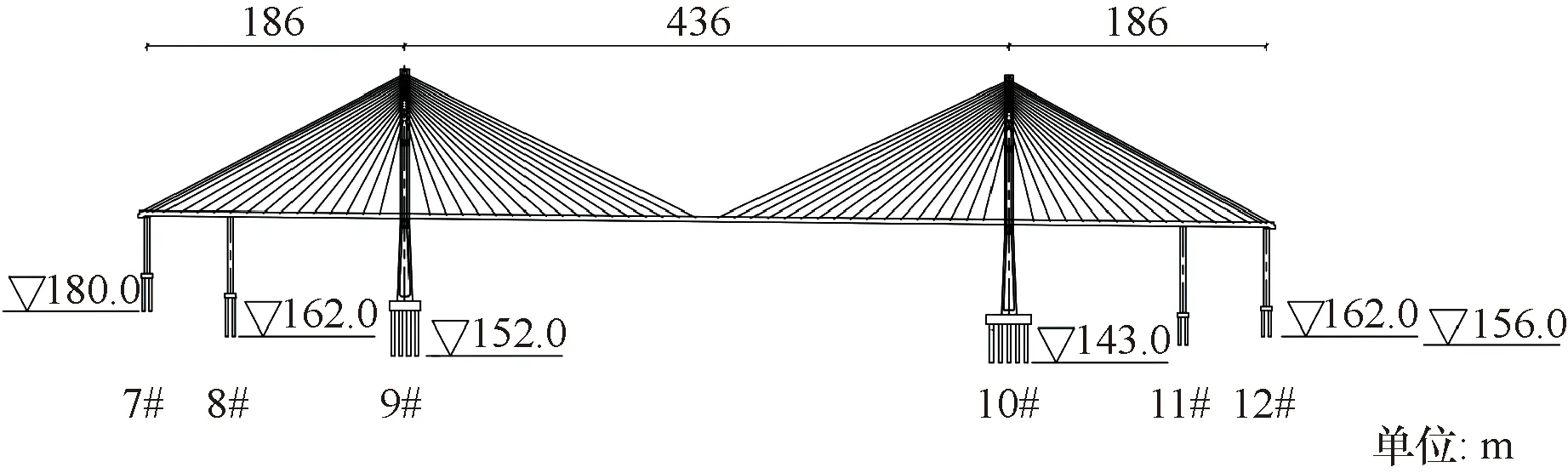
7#～12#表示桥墩编号图1 斜拉桥整体布置图Fig.1 Overall layout of cable-stayed bridge

1.2 桥区水域情况

通过调查，距离工程最近的水工建筑物主要有某危险品码头、某航道基地趸船和天然气管道穿越工程以及某油码头。

1.3 桥区河段水流条件

桥梁在长江干流上，河道呈“U”形，水流条件见表1。

表1 桥区河段水流条件Table 1 River flow conditions in bridge area

从表1可以看出，低水期桥区河段水流流速较小；高水期河道中水流流速较大且桥区河段河道弯曲，规划航道中心线与水流流向的夹角较大，相对横向流速较大。由于水面宽度较大，工程河段整体较平顺，主流平面流速变化较均匀。选取的低水位、高水位和洪水位的流速分别是1.5、4、5.5 m/s。

1.4 可达性分析

船舶在最高通航水位(198.05 m)、洪水位(203.06 m)之间水位通航时，9#～12#墩都会发生船撞的风险，其中9#、10#墩位于主航道区域；船舶在最低通航水位(175.70 m)通航时，仅10#墩会发生船撞的风险。

2 桥梁自身抗撞能力分析

2.1 模型建立

在船撞力的作用下，墩柱在墩底处产生最大弯矩和剪力，桩基在桩顶处产生最大弯矩和剪力，一般情况下，可以将墩柱底截面和桩顶截面作为最危险控制截面进行计算。通过Xtract软件进行桥墩最危险截面处弯矩-曲率曲线的模拟计算。在截面分析软件Xtract中输入材料参数，按照实际截面尺寸和配筋建模，网格的划分根据截面尺寸和分析效果进行划分，得出弯矩-曲率曲线。弯矩-曲率分析一般分两个阶段分析，分别是混凝土开裂、钢筋屈服两个阶段，该墩柱具有正常配筋率，受拉钢筋首先屈服，取钢筋屈服时的弯矩作为截面的极限弯矩。

建立的极限弯矩计算模型各控制截面的截面形状及网格划分情况见图2。为了确定该斜拉桥主桥自身内力，通过MIDAS建立桥梁整体模型，如图3所示。

图3 主墩及辅墩有限元内力计算模型Fig.3 Finite element internal force calculation model of main pier and auxiliary pier

2.2 桥墩自身抗撞能力计算

参考文献[15]中指出，当桥墩受到大小为P的船撞力作用时，船撞力在各桥处产生的内力F′计算公式为

(1)

式(1)中：F′为船撞力在桥产生的内力，此处为极限弯矩，kN·m；P为船撞力，kN；F为桥墩施加1 000 kN船撞力得到的桥墩内力，此处为截面弯矩，kN·m。反之，则可以得到船撞力P，即桥墩自身抗撞能力，按式(2)计算。

(2)

在MIDAS软件计算中，对桥墩施加1 000 kN的单位荷载，作用在墩底和桩顶以上2 m位置中点处[16]，荷载类型为节点荷载(船只或漂浮物的撞击力)，角度为水平方向横桥向正撞(0°)，从而得到桥墩内力，即截面弯矩。由式(2)得到主墩及辅墩在不同水位下的桥墩抗力。截面弯矩、极限弯矩、桥墩自身抗撞能力的计算结果见表2。

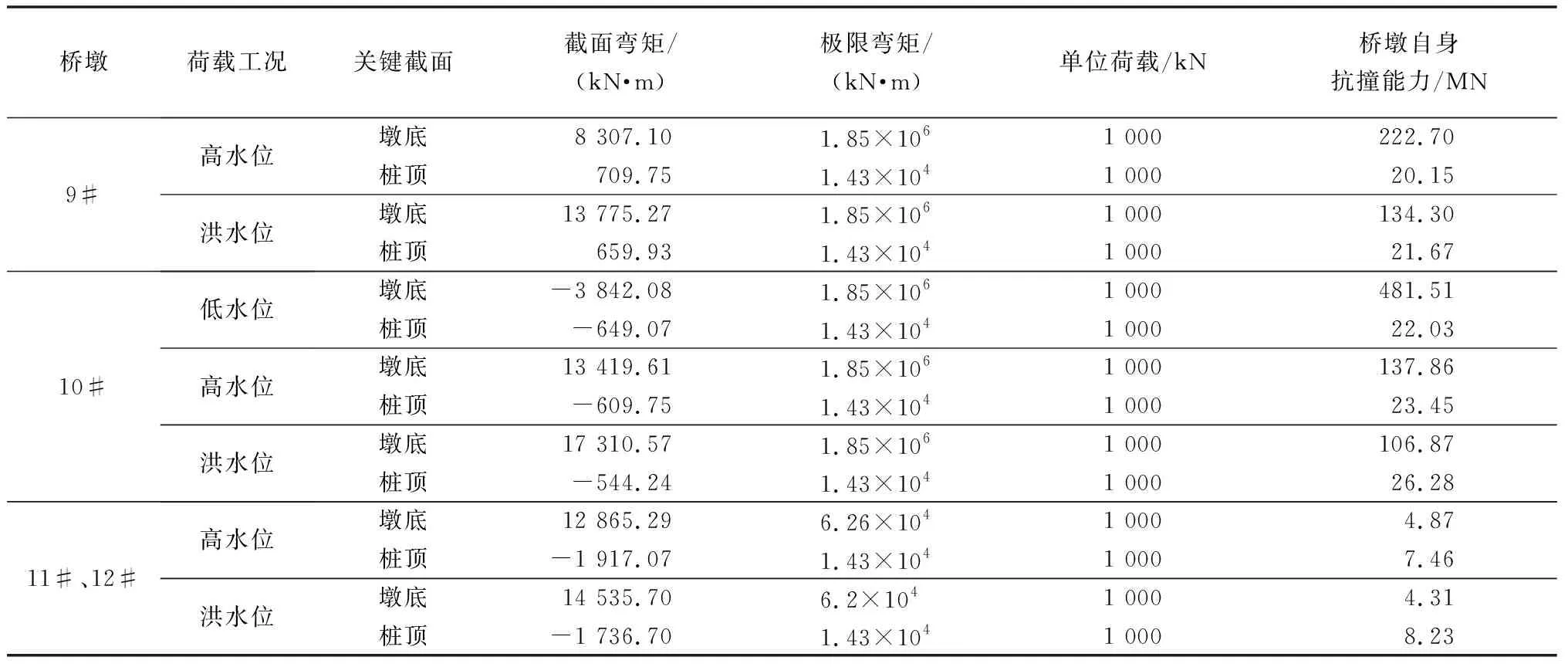
表2 斜拉桥墩自身抗撞能力计算结果Table 2 Calculation results of self-collision capacity of cable-stayed bridge pier

3 船舶撞击力计算

3.1 代表船型及通航量预测

该斜拉桥工程河段代表船型按5000 t级干散货船考虑[17]。高水期可通行更大吨位船舶，验算中主墩(9#、10#)的撞击船舶按7 000 t级干散货船考虑，辅墩(11#、12#)的撞击船舶按2 000 t级干散货船考虑。根据2014—2017年的实测年通航量，预测2025年、2030年和2035年的船舶通航量分别为18 250、22 265和23 360艘。主要船型参数见表3。

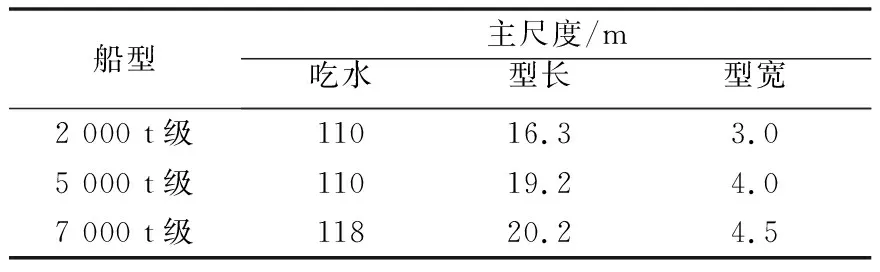
表3 工程河段船型尺度表Table 3 Ship type scale table of engineering reach

3.2 偏航撞击速度

桥区河段航行船舶(队)的航速参数：船舶上行航速为12 km/h，下行航速为20 km/h。综合考虑安全因素以及河道里程综合影响后，采用《公路桥梁抗撞设计规范》[18]公式计算得到船舶通过各涉水桥墩时的撞击速度，计算公式见式(3)，船舶撞击速度曲线图见图4。

图4 船舶撞击速度曲线Fig.4 Ship impact velocity curve

(3)

式(3)中：V为设计船舶撞击速度，m/s；VT为船舶的正常航行速度，m/s；X为桥墩中心线至航道中心线的距离，m；Xc为航道中心线至航道边缘距离，m；XL为航道中心线至3倍船长的距离，m；VL为水域特征流速，m/s；Vmin为船舶最小设计撞击速度，m/s。

船舶通过各涉水桥墩时的撞击速度计算结果见表4。在综合考虑安全因素后将撞击速度取为航道内正常行驶速度，即船舶通过9#主墩时撞击速度为5.5 m/s(船舶上行)，10#主墩时撞击速度为8.5 m/s(船舶下行)。11#、12#桥墩仅考虑洪水位时船舶失控撞向11#、12#桥墩的情况，取5.5 m/s(船舶下行)。

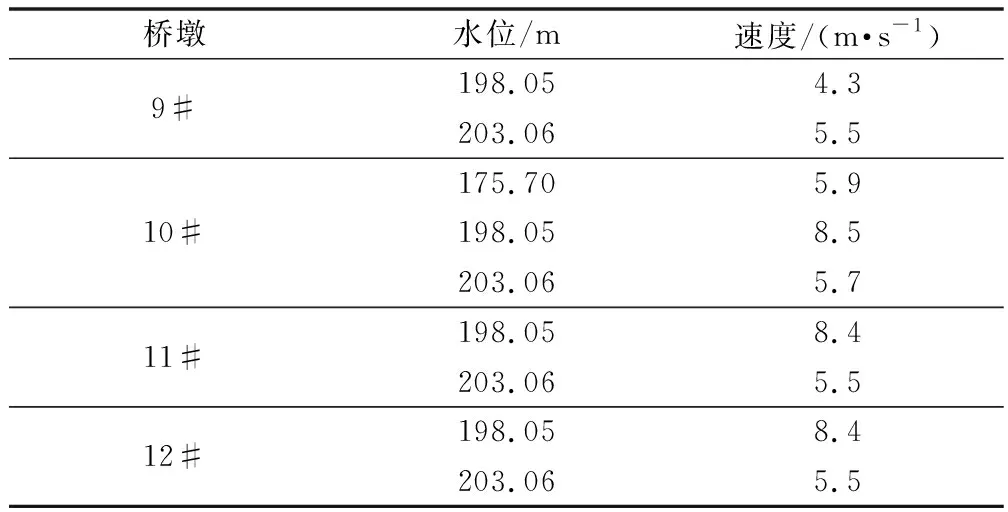
表4 船撞速度计算结果Table 4 Calculation results of ship collision velocity

3.3 船撞力计算

为了更为真实地预测船撞力，采用AASHTO规范公式、《公路桥梁抗撞设计规范》公式与有限元仿真结果对比分析确定船撞力。

3.3.1 AASHTO规范公式

依据AASHTO规范中相关规定，船撞力计算公式为

(4)

式(4)中：P为船舶最大撞击力，N；M为船舶载重量，t；v为船舶撞击速度，m/s。

3.3.2 《公路桥梁抗撞设计规范》公式

根据《公路桥梁抗撞设计规范》规定，和桥梁撞击时，按式(5)计算，即

F=0.015M0.7V

(5)

式(5)中：M为满载排水量，t；V为船舶撞击速度，m/s。

3.3.3 有限元仿真模拟

采用ABAQUS建立7 000 t级和2 000 t级干散货船有限元模型分别撞击斜拉桥主墩和辅墩。全船采用壳单元进行建模，对主墩及辅墩在3种工况水位(最低、最高通航水位和洪水位)情况下进行船撞力计算。船舶有限元模型如图5所示。由于船撞发生时间极短，且撞击力的大小主要和船艏及墩的构造相关，受上部结构的影响较小，该部分粗略化建模。桥墩撞击计算模型平面视图见图6。

图5 船舶有限元模型Fig.5 Ship finite element model

图6 桥墩撞击计算模型平面视图Fig.6 Plane view of pier impact calculation model

3种船撞力计算结果见表5。可以看出，有限元仿真结果与AASHTO规范及公路桥梁抗撞设计规范的计算结果有一定的差异。

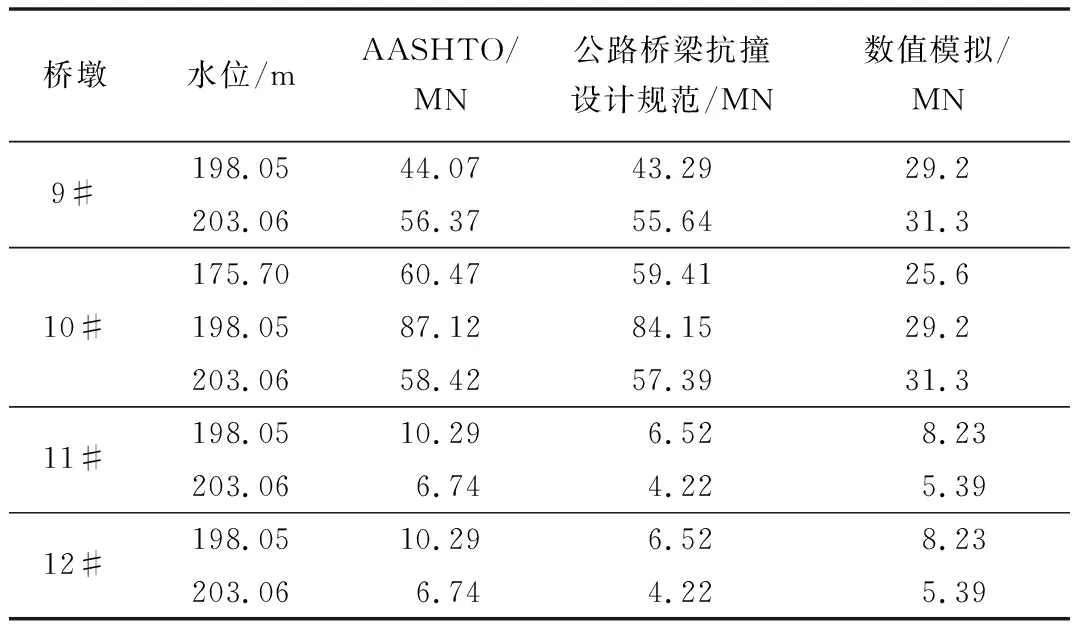
表5 船撞力计算结果Table 5 Calculation results of ship collision force

9#与10#桥墩在各个水位时，公路桥梁抗撞设计规范与AASHTO规范的船撞力计算结果较为接近。其中10#桥墩在198.05 m水位时，有限元仿真结果与AASHTO规范的船撞力计算结果差异最大。11#与12#桥墩在各个水位时，AASHTO规范计算结果与有限元仿真结果较为接近。其中11#与12#桥墩在198.05 m水位时，公路桥梁抗撞设计规范与AASHTO规范的船撞力计算结果差异最大。产生差异的原因可能是各个规范的公式计算侧重点不一样，以及实际船舶与有限元模型的差异。

由于AASHTO规范的船撞击计算结果都大于公路桥梁抗撞设计规范计算结果与有限元仿真结果，为了偏于安全考虑，船撞力都采用AASHTO规范计算结果。

4 桥梁船撞风险分析

4.1 年撞击概率

涉水桥墩年撞击频率可按式(6)计算。

Fimp=NPAPG

(6)

式(6)中：N为可撞损桥墩的分类船舶年通航量；PA为船舶偏航概率；PG为船舶与桥墩撞击的几何概率。

根据代表船型及通航量预测，计算得到该斜拉桥在最低通航水位、最高通航水位和洪水位时船舶撞击大桥的年撞击概率，见图7～图9。

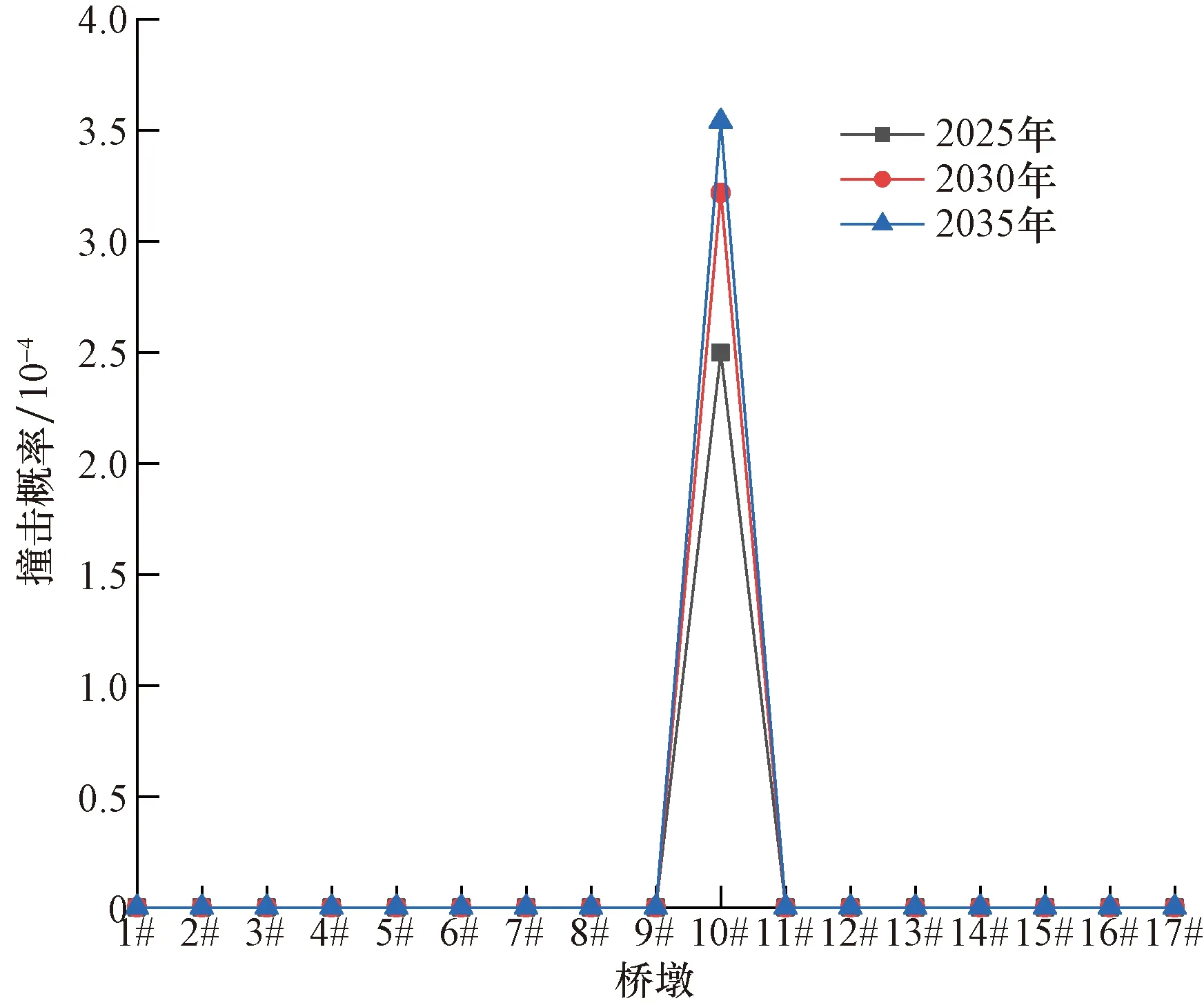
图7 175.70 m水位时船舶年撞击频率分布Fig.7 Distribution of annual impact frequency of ship at 175.70 m water level

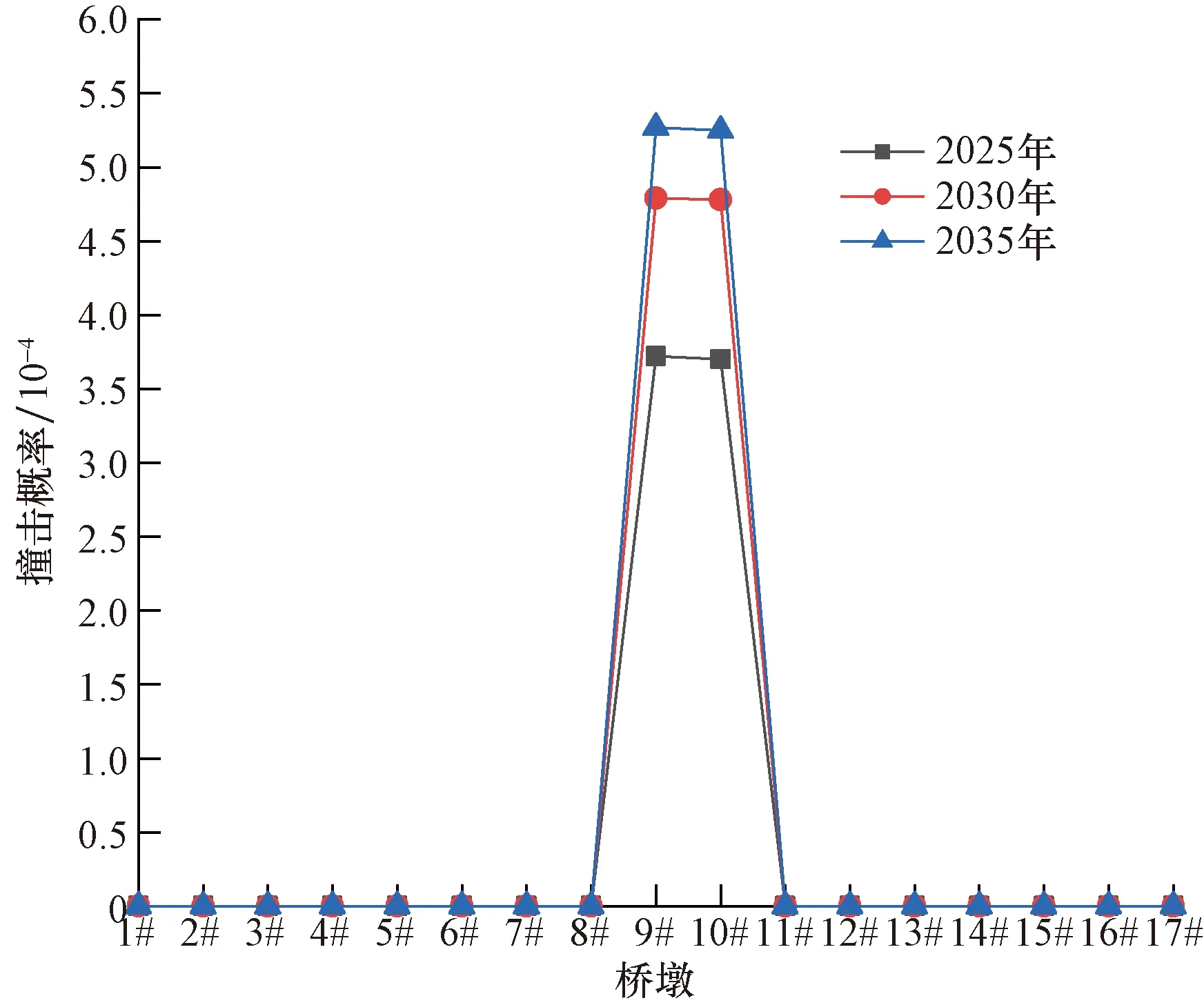
图8 198.05 m水位时船舶年撞击频率分布Fig.8 Distribution of annual impact frequency of ship at 198.05 m water level

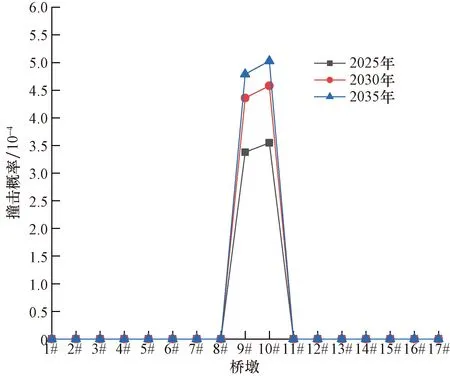
图9 203.06 m水位时船舶年撞击频率分布Fig.9 Distribution of annual impact frequency of ship at 203.06 m water level

4.2 年撞损概率

桥墩年撞损概率与桥梁自身抗撞能力和船舶撞击力有关，可按照式(7)计算。

(7)

式(7)中：PC为桥墩受船舶一次撞击的撞损率；H为桥墩抗撞能力，N；P为船舶最大撞击力，N。

结合前文计算的桥梁自身抗撞能力和船舶撞击力，得到年撞损概率，见图10～图12。

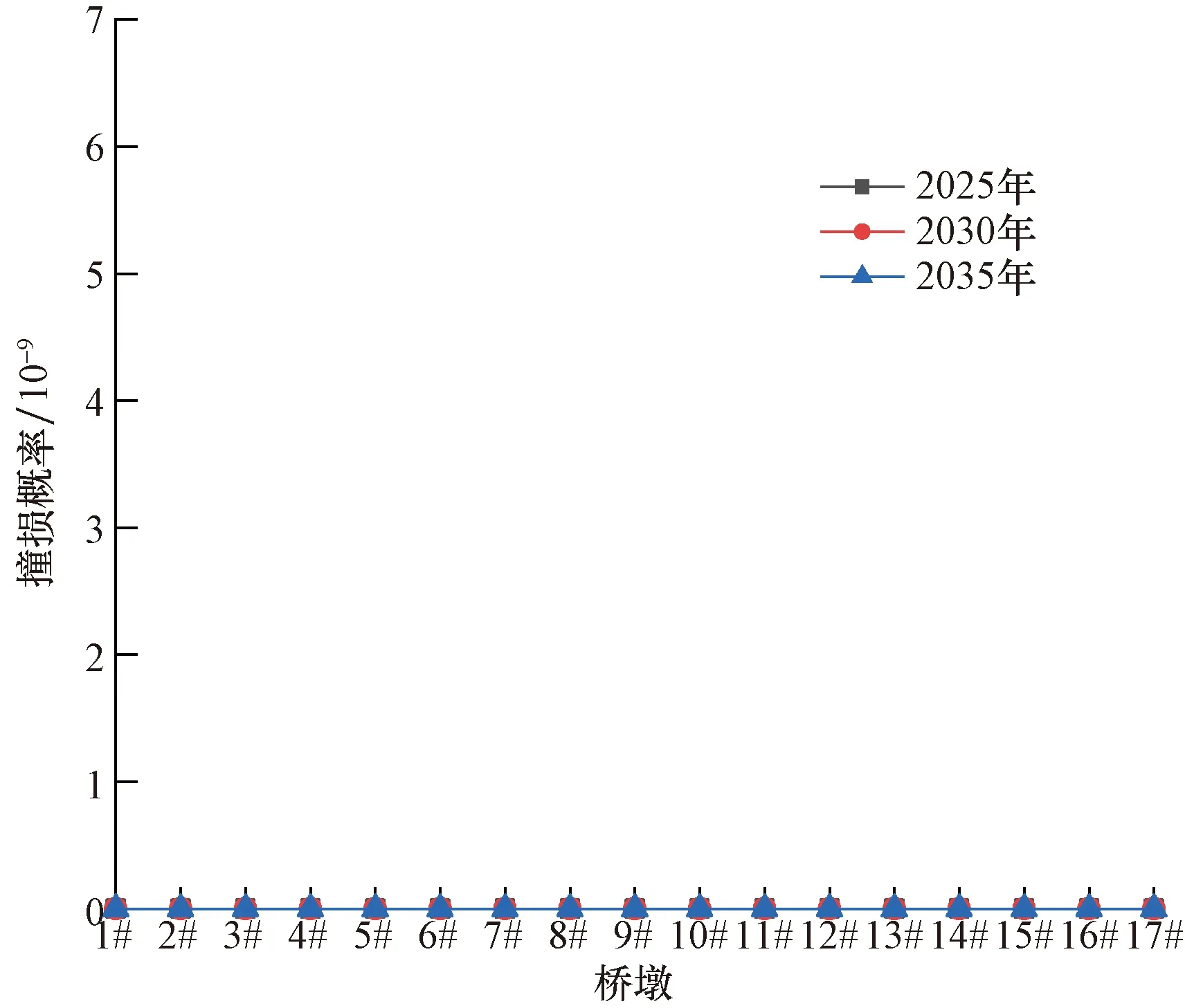
图10 175.70 m水位时年撞损频率分布Fig.10 Distribution of annual damage probability at 175.70 m water level

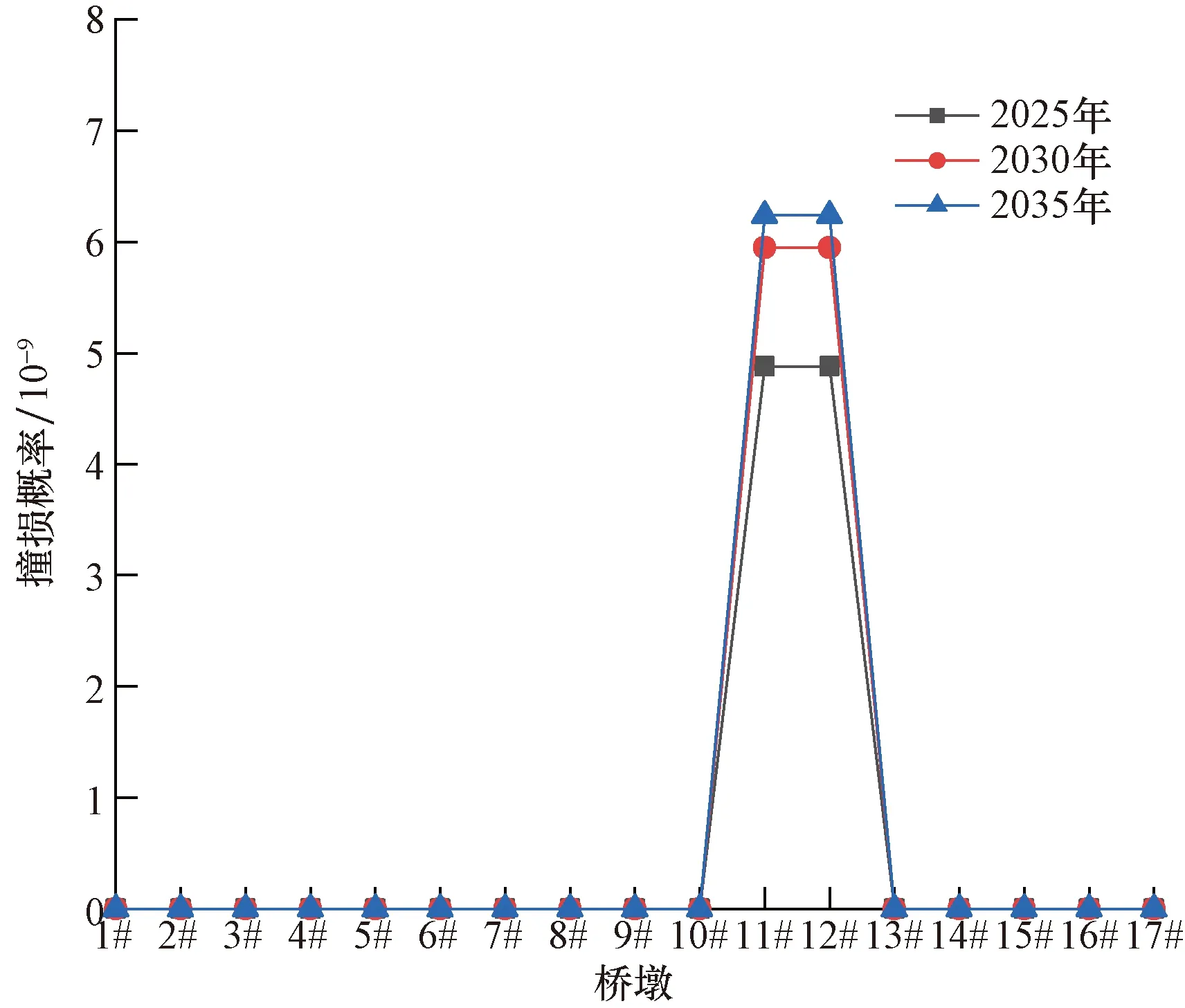
图11 198.05 m水位时年撞损频率分布Fig.11 Distribution of annual damage probability at 198.05 m water level

图12 203.06 m水位时年撞损频率分布Fig.12 Distribution of annual damage probability at 203.06 m water level

4.3 风险分析

依据AASHTO规范中相关规定，编制如图13所示的评估矩阵，对于关键性桥梁，其年撞损频率小于10-4，对于一般性桥梁，其年撞损频率小于10-3被认为是可以接受的。

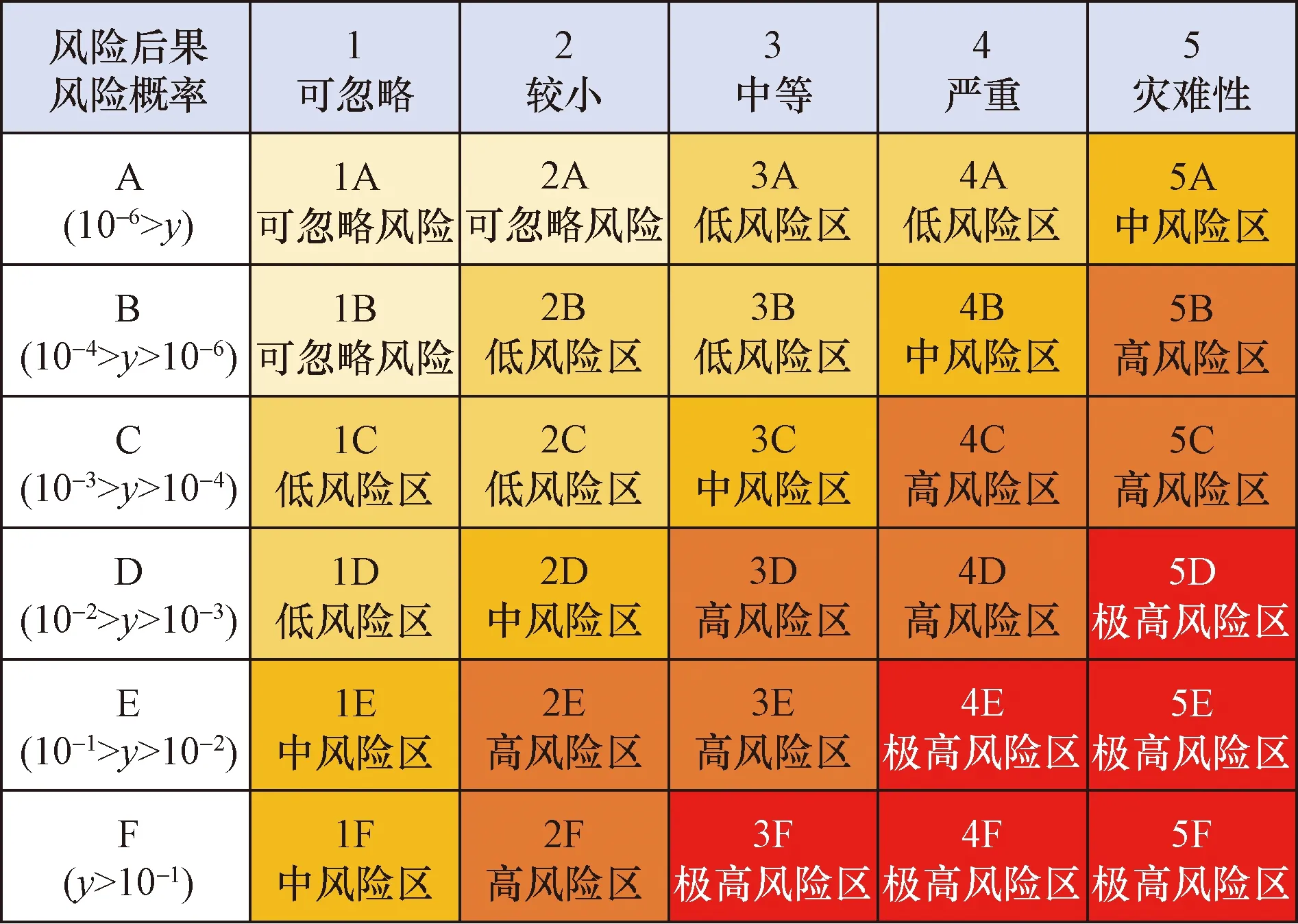
y为计算得到的风险概率图13 桥梁船撞风险评估矩阵Fig.13 Bridge-ship collision risk assessment matrix

由图7～图12可知，随着船舶流量的增加，全桥年撞击频率和年撞损概率逐年增加，由图13船撞风险的概率水平分级，大桥撞击概率发生在10-4～10-3区间，风险水平等级为C级(较难发生)；撞损概率低于10-6，风险水平等级为A级(不可能发生)，因此，该桥墩的年撞击概率及撞损概率都在可接受范围内。

5 结论与建议

(1)按照2025年、2030年与2035年通航量，175.70、198.05和203.06 m水位时，船舶撞击9#～12#桥墩的年撞击概率和年撞损概率均在可接受风险值内。

(2)由于该桥位于长江干流上，为关键性桥梁，考虑到桥墩混凝土局部损伤，难以修复，同时为防止船舶发生海损事故，建议9#、10#墩增设附着于桥墩的变截面防撞浮箱结构。

(3)11#、12#墩有一定的撞损概率，建议增设相应的防撞设施，设置警示标牌和禁止通航标，并准备相应的应急预案。