拖曳锚在浮式风机中的设计计算方法

康思伟，栾辰宇，张雨蓉，李飒

(1.中海油融风能源有限公司，上海 200050； 2.天津大学建工学院，天津 300072)

风能作为一种可再生的能源，其开发和利用拥有广阔的潜力和前景[1]，其锚固基础的设计计算也越来越受到大家的关注[2]。海上风力发电风机基础形式大致可以分为两大类：固定式基础和漂浮式基础；固定式海上风机基础主要适用于近海岸0～60 m的水深海域，而漂浮式海上风机基础主要适用100 m以上水深海域，甚至更深的海域。截至2020年，已经建成的浮式风机场地20余处，其中绝大部分为示范项目，用于商用的不超过3处。其中的WindFloat Atlantic采用了拖曳锚作为浮式风机永久性锚固基础[3]。

拖曳锚是用系泊缆水平拖曳，将锚爪插入海底。锚爪是一个承载板，提供锚的大部分承载能力。锚杆控制系泊张力的作用线作用在锚爪的角度和位置。一般而言，拖曳锚由于安装方便, 同时也易于回收，因此是一种非常具有吸引力的锚固基础的选择。

拖曳锚的一个潜在缺点是无法实现精确定位。垂直定位的不确定性转化为承载能力的不确定性,此外，拖曳锚在土体中形态的不确定性也影响到其承载力的准确评估,它们传统上主要用于临时系泊，而不是永久设施。近年来拖曳锚已从传统的船舶锚发展为设计复杂可用于半永久系泊系统的高承载力锚。

目前用于计算拖曳锚承载力的方法主要有3种，第一种是经验法，经验法是根据工程或试验中实测数据总结得到的经验公式与参考设计表，用于计算拖曳埋置锚的最大拖曳距离与承载力。目前经验法相关数据主要由锚制造商提供[4]。第二种是理论计算方法，经验相关性在预测锚性能方面无疑具有很大的实用价值。然而，纯经验方法有固有的局限性。基于均匀厚度矩形板的理想化板锚的简化分析是目前常用的理论分析方法。由于拖曳锚的承载力与其埋深具有直接关系，因此在承载力的计算过程中，有必要评价拖曳锚的嵌入过程。在分析过程中，结合锚链的形态[5]，采用极限平衡或极限分析方法通过位移增量的计算确定拖曳锚的贯入过程，并进而确定拖曳锚的承载力[6-7]。第三种方法是有限元法，近年来随着数值模拟技术的飞速发展，大变形有限元如耦合欧拉-拉格朗日(coupled Euler Lagrange，CEL)法被用来计算拖曳锚的贯入[8]。

由于拖曳锚的精确定位是拖曳锚研究中的关键问题，毋晓妮等[9]研究了黏土中浅埋拖曳锚的运动性能，并指出在埋深较浅的情况下，埋深比和方位角对土体中的屈服面均有影响。张春会等[10]基于增量迭代法提出了预测拖曳锚嵌入运动轨迹和系泊点拉力的模型。

尽管大量学者对这一问题展开了很多研究，到目前为止，并没有一种方法可以解决拖曳锚精确定位的问题。而在这些方法中，对于黏土中的拖曳锚，O’Neill等[11]提出的采用破坏包络线预测拖曳锚安装行为的方法被广泛使用。在此方法中，锚链方程用于计算拖曳锚所受力的大小和角度；锚杆的阻力考虑锚杆上的法向力和滑动力。使用锚爪的破坏包络线确定锚爪上的荷载。通过确保拖曳锚(包括锚爪、锚杆和锚链上的力)在每个推进步骤处于平衡状态，预测锚定轨迹。

尽管目前有关拖曳锚问题的分析研究仍然存在很多问题，但这无法阻止拖曳锚在实际工程中的广泛应用。考虑到拖曳锚在浮式风电中具有广阔的应用前景，现以Hywind Scoland风场的设计计算条件为基础，采用设计图表法、理论计算法以及有限元方法对拖曳锚的承载力进行计算，并根据计算结果提出拖曳锚作为浮式风电锚固基础的设计计算流程，对其应用于浮式风电中需要注意的问题进行评价。

1 拖曳锚的计算方法

1.1 设计图表法

以Vryhof公司提供的拖曳锚设计方程为例说明利用设计图表进行拖曳锚承载力的计算的具体方法，如表1所示。

表1 Vryhof公司拖曳锚的设计方程Table 1 Design equation for drag embedded anchor of Vryhof company

1.2 理论计算法

采用Neubecker等[5]提出的方法计算系泊缆的张力。将拖曳锚通简化成如图1的形式。即假设锚爪为一个长度为Lf和厚度为tf的简单条形机构，拖曳锚相关尺寸与位置示意图如图1所示。

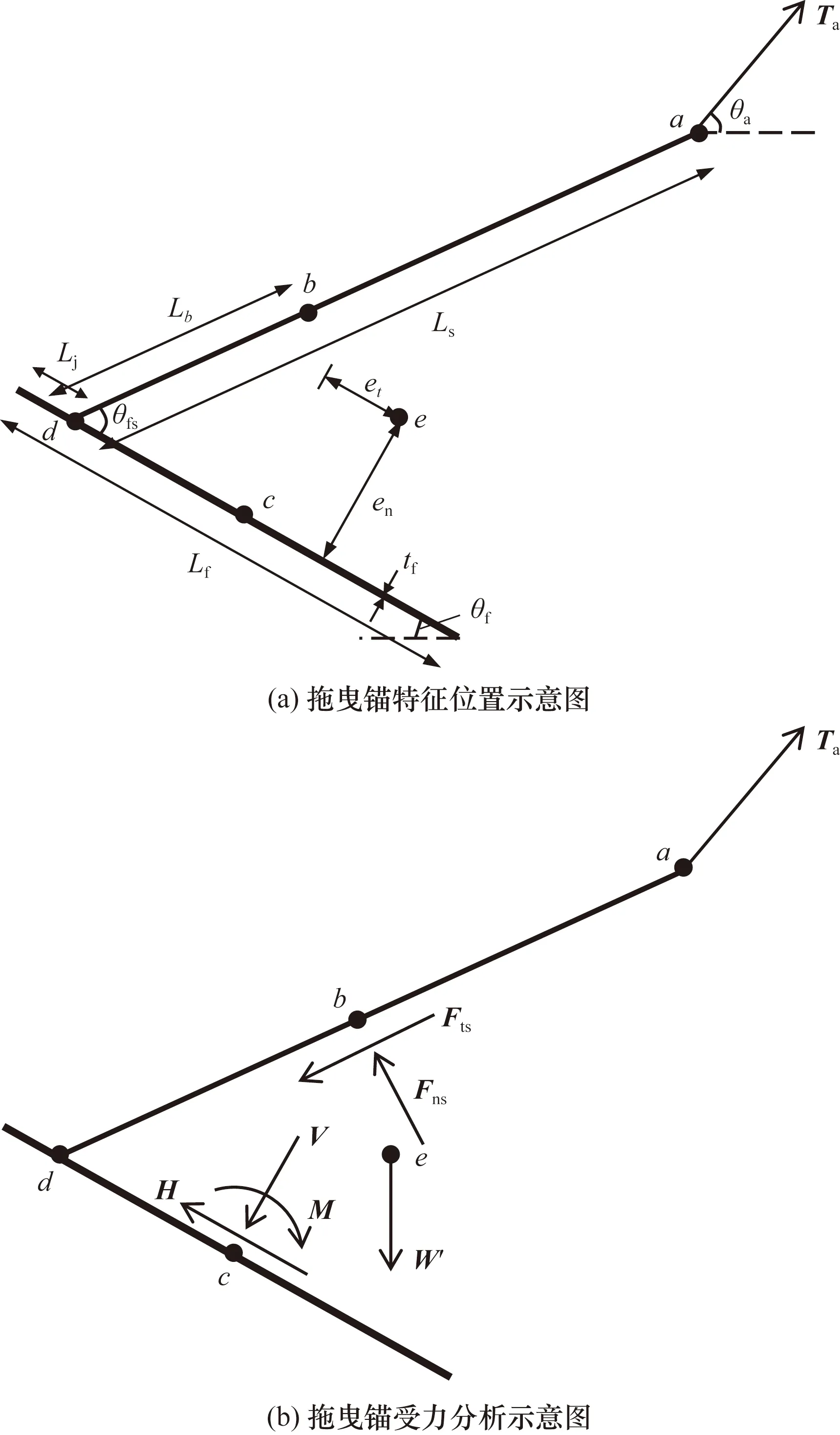
图1 拖曳锚特征位置和受力分析示意图Fig.1 Characteristic position and loading analysis of drag embedded anchor

长度为Ls的锚杆以杆-爪角θfs刚性连接。在锚贯入过程的某一时刻，锚爪和锚杆分别对应角度θa和θf。此处分析是针对极限状态进行的，此时施加的张力Ta对应锚的极限载荷能力。

拖曳锚位置确定利用了几个特征点：系泊点位置(系泊张力施加位置)a，锚杆受力点b，锚爪中心点c，锚杆与锚爪连接点d，拖曳锚重心e。锚杆受力点与锚杆锚爪连接点的距离Lb，锚爪相对于连接点d后侧长度Lj。重心相对于锚爪中心点c的垂向与水平向距离设置为en与et。

拖曳锚的受力，除了系泊点处系泊张力Ta，还包括锚杆法向承载力Fns与切向力Fts，锚自身重力W′，锚爪自身所受的切向力H，竖向力V与转矩M(以中心点e为参考点)。其中，锚杆法向力Fns可表示为土单位承载力乘法向受力面积，锚杆切向力Fts可表示为单位切向力乘锚杆表面积。考虑力与转矩的平衡，锚爪中心点c上的法向力V、切向力H和力矩M可以定义为

V=Tasin(θα+θf)-W′cosθf+Fnscosθfs-Ftssinθfs

(1)

H=Tacos(θα+θf)+W′sinθf-Fnssinθfs-Ftscosθfs

(2)

M=Ta[Lssin(θα+θf-θfs)-(Lf/2-Lj)×

sin(θα+θf)]+Fts(Lf/2-Lj)sinθfs+

Fns[Lb-(Lf/2-Lj)cosθfs]-

W′(etcosθf+ensinθf)

(3)

锚杆受力点与锚杆与锚爪连接点的距离可表示为

(4)

式(4)中：Sur=kLssin(θfs-θf)/Su0，考虑锚爪上力的相互作用，采用破坏包络面的表达式为

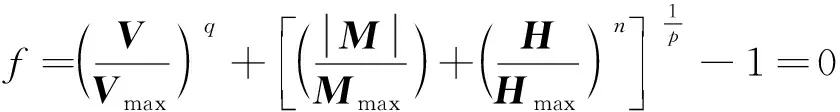
(5)

式(5)中：Vmax、Mmax和Hmax定义拖曳锚的法向、切向和弯矩的单轴承载力(代表独立作用时的最大载荷)；指数m、n、p和q定义破坏包络表面的形状。

根据上述计算方法，采用图2所示的计算流程编制程序，进行拖曳锚的贯入深度和承载力计算。

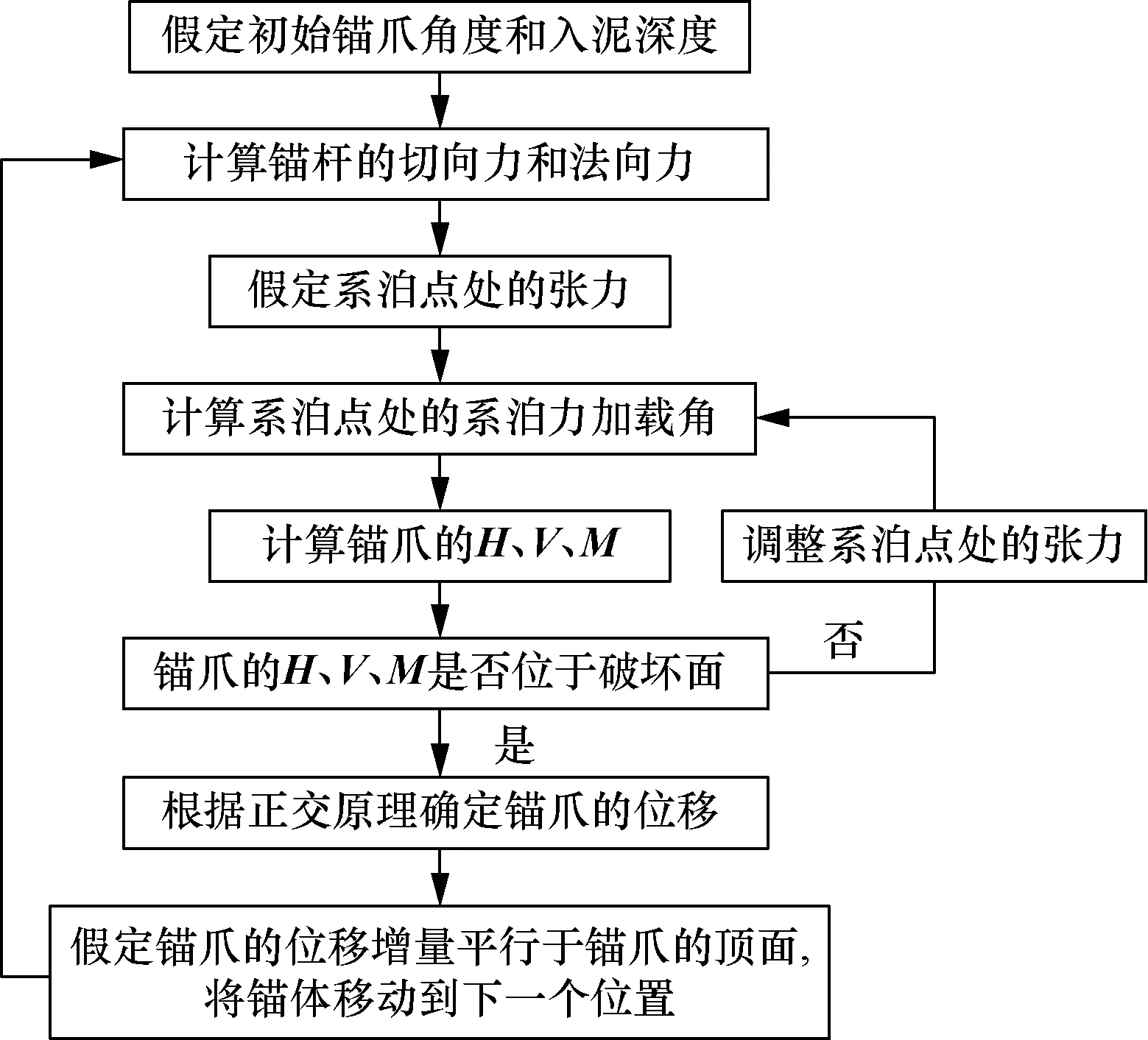
图2 黏土中拖曳锚计算流程图Fig.2 Calculation flow chart of drag embedded anchor in clay

2 工程背景

苏格兰Hywind是世界上第一个商用浮式风电场。该浮式风电场坐落于苏格兰北部的海洋中，风场所在地的水深为95～120 m，平均风速10.1 m/s,平均波高1.8 m。该风机的基本情况如表2所示[12]。

表2 Hywind风机的各部分尺寸和重量Table 2 Size and weight for Hywind turbine turbine

该风场地层主要由两类中等强度黏土组成，黏土参数[13]如下。

分别对临床有效率和PCO2绘制倒漏斗图，见图8、9。结果显示纳入研究数据点基本分布在对称轴的两侧，且位于倒漏斗图的顶部，但临床有效率的个别数据点在倒漏斗图中下部、PCO2的个别数据点在倒漏斗图线边缘，提示可能存在发表偏移。

一种黏土为均质黏土，平均土强度Su=30 kPa。

一种黏土为强度线性增长的黏土，表层土强度Su0=15 kPa，土强度梯度k=2 kPa/m。

在实际工程中，设计载荷为2 000 t，采用了高度16 m、直径5 m的吸力锚作为锚固基础。

3 拖曳锚可行性分析

3.1 设计图表法计算

选择Vryhof公司MK6型锚，首先根据厂商的设计图表法进行拖曳锚的选型。拖曳锚的拖曳距离以及承载力如表3所示。

表3 拖曳锚的贯入深度及承载力Table 3 Penetration depth and capacity of drag embedded anchor

从表3中可以看到，采用Vryhof公司40 t和50 t的MK6型锚均可以满足设计要求，为更加经济，选择40 t的拖曳锚进行进一步的计算。

3.2 理论计算法计算

同时，采用理论计算方法对拖曳锚的贯入深度以及承载力进行进一步的分析。计算过程中所采用的计算参数如表4所示[15]。

采用表4的计算参数，得到在不同土质条件下拖曳锚的贯入深度与拖曳距离的关系以及拖曳锚承载力与贯入深度之间的关系，如图3和图4所示。

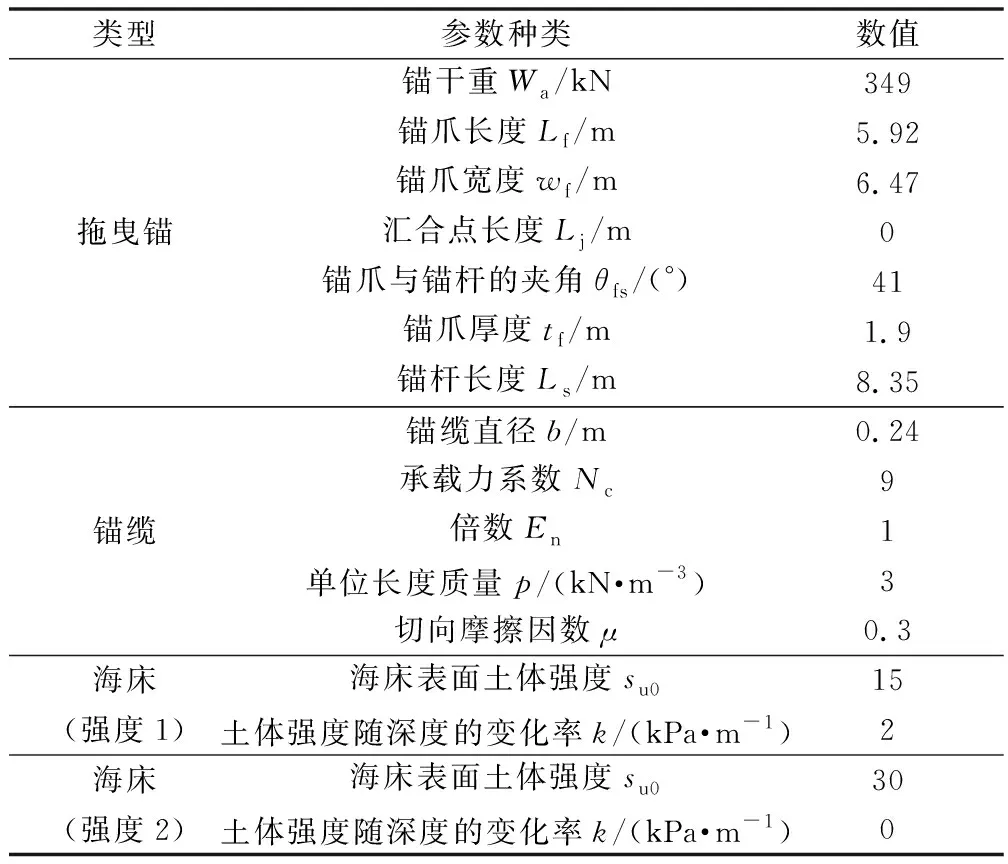
表4 40 t MK6拖曳锚的计算参数Table 4 Parameters for MK6 in 40 t

从图3和图4可以看到，对于均质黏土Su=30 kPa的情况，75 m拖曳距离对应9.7 m贯入深度，拖曳锚最终拖曳力为1 400 t。对于表层强度Su0=15 kPa，土强度梯度k=2 kPa/m的黏土，75 m拖曳距离对应14.3 m贯入深度，拖曳锚最终拖曳力为2 240 t。

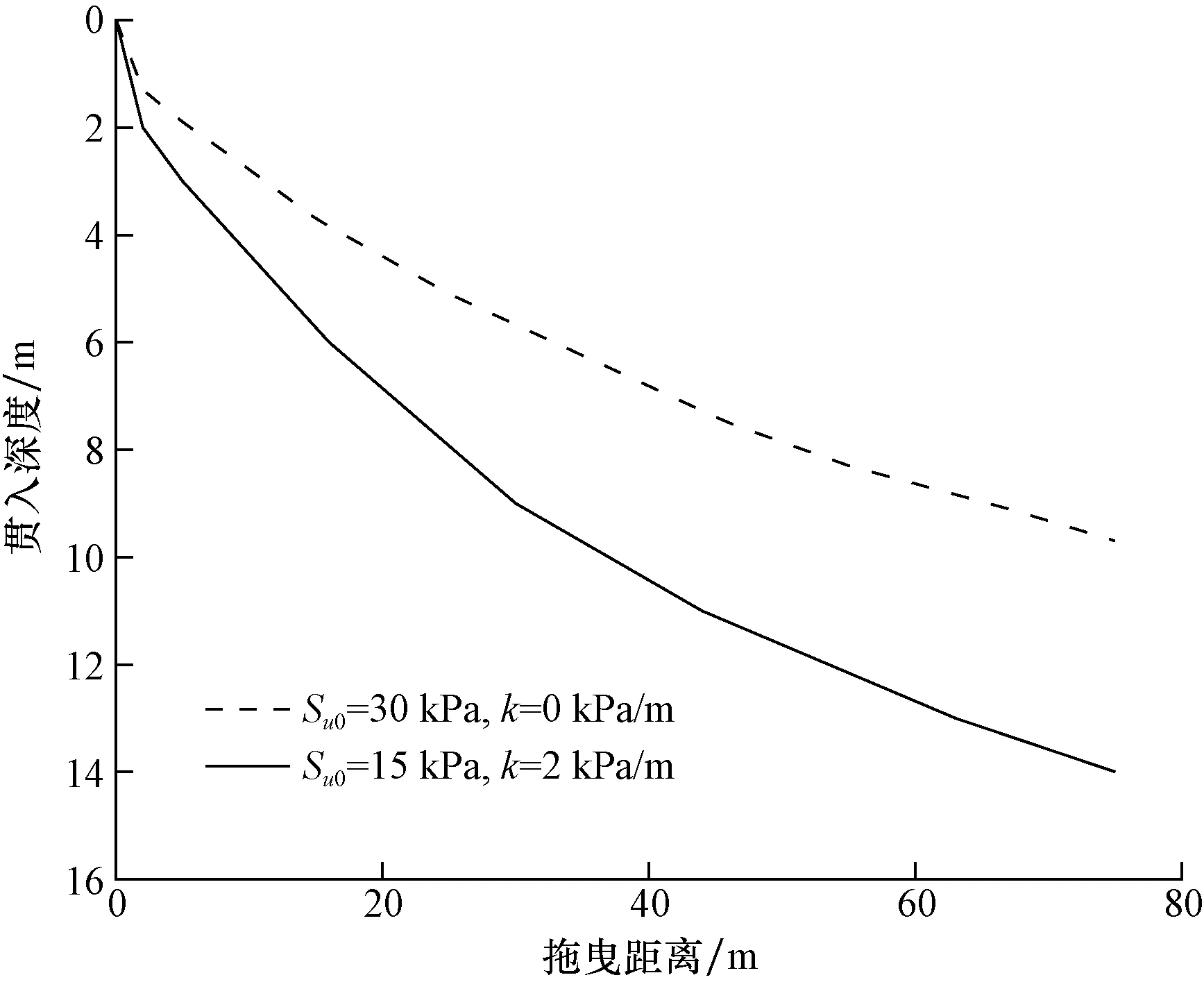
图3 40 t MK6锚贯入深度随拖曳距离变化曲线 Fig.3 Relationship of penetration depth and dragging distance of 40 t MK6

图4 40 t MK6锚拖曳力随拖曳距离变化曲线Fig.4 Relationship of moor loading and dragging distance of 40 t MK6

可以看到，仅Su0=15 kPa，k=2 kPa/m的黏土计算结果与制造商提供的数据(2 200 t)相似，而对于Su=30 kPa的均质黏土，拖曳锚承载力数值偏小。

从图3、图4计算结果可以看到，拖曳锚的设计计算对土体强度的变化较为敏感，上述两种计算在贯入深度范围内的土体强度的平均值均为30 kPa，但其贯入深度和最终承载力相差达到70%。这主要是因为对于强度随深度变化的土体条件，拖曳锚的贯入深度明显大于均质强度的土体条件。因此在拖曳锚的设计计算时，需要考虑土体强度随深度的变化，采用平均值进行拖曳锚承载力计算会低估拖曳锚埋入深度，导致计算所得承载力偏低。同时也可以看到，制造厂商提供的数据仅可做初始承载力的估算使用，拖曳锚在具体场地的承载力需要更加详细的计算。

3.3 有限元法

为进一步评价拖曳锚的承载性能，针对第一种土质情况，即黏土为均质黏土，平均土强度Su=30 kPa情况的拖曳锚承载力展开有限元分析。

由于拖曳锚的拖曳过程采用有限元模拟时间成本过高，在评价拖曳锚承载力的过程中，采用将锚体分别埋置于由图表法获得的贯入深度14 m，以及由理论法获得的贯入深度7.9 m来计算拖曳锚的承载力。

给定计算得到的拖曳锚拉力角与拖曳力(拖曳力为设计拖曳力20 000 kN)，评估拖曳锚能否在该力作用下保持一个稳定状态。由于拖曳锚可能产生较大旋转，因此采用有限元大变形分析(CEL)。由于不模拟拖曳过程，拖曳锚的初始锚爪角设置为0°，拖曳锚与土体模型剖面如图5所示。

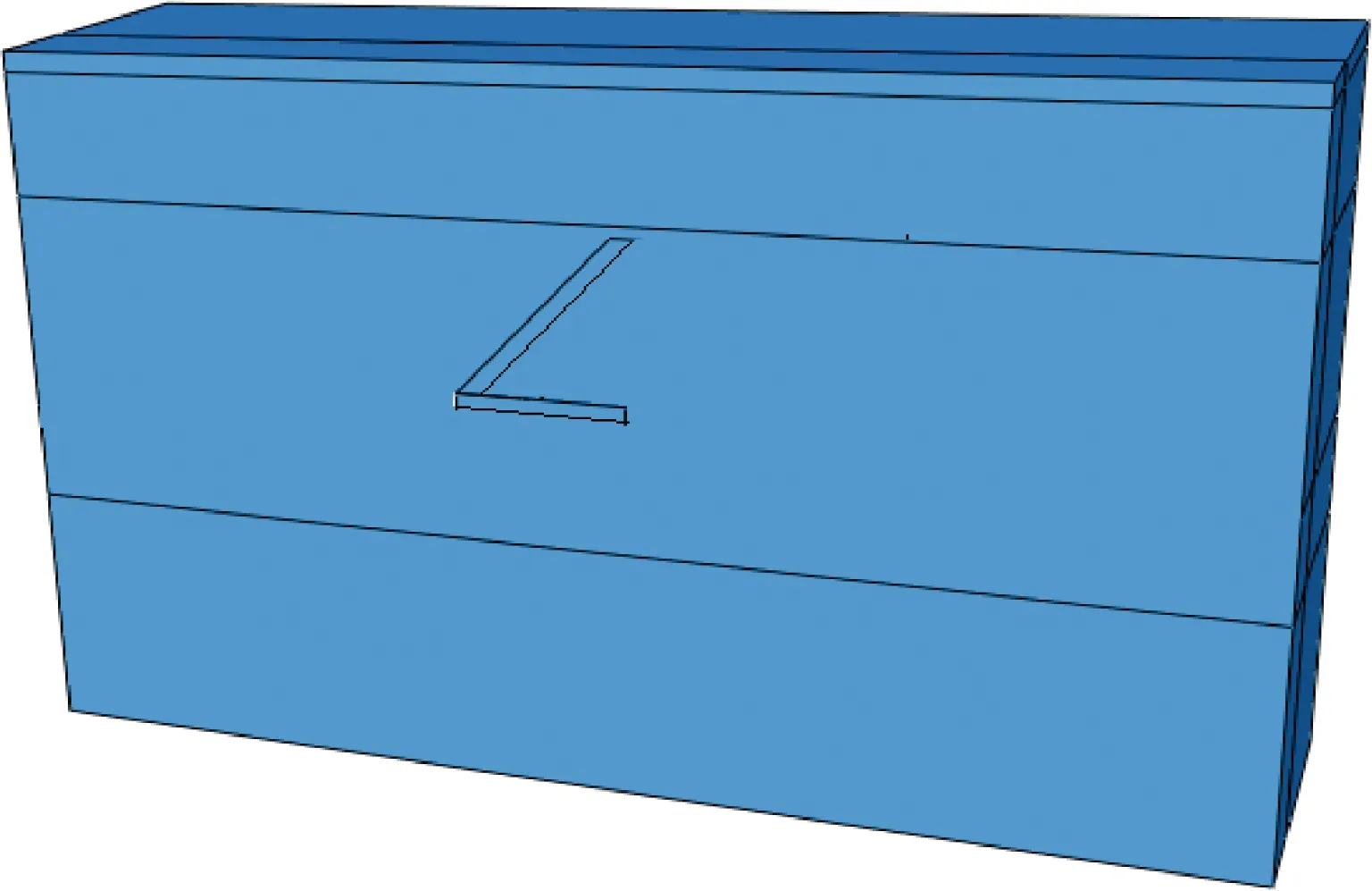
图5 拖曳锚与土体模型剖面Fig.5 The section for CEL model

拖曳锚会在对应拉力下旋转并达到稳定，拖曳锚在拉力不断增加情况下，土体塑性应变区变化以及达到稳定状态时y-z截面的塑性应变区如图6所示。

图6 拖曳锚受拉后的塑性应变区变化Fig.6 The development of plastic zone in clay

由塑性应变图可知，锚体在拉力下旋转，并在周围形成塑性应变区。随着锚体旋转程度的不断提高，塑性区范围不断扩大，其中锚体底部塑性应变最大。由于锚体在旋转过程中也有水平位移，为考察锚体的位置变化，选取锚爪的中点作为参考点，首先考察锚爪中点处的旋转角度随水平位移的变化，如图7所示。可以看出随着锚爪中心位置的水平位移的增加，旋转角度会不断增加，但旋转角度的增幅会随着水平位移的增加而逐渐降低，逐渐使得旋转角度趋于平稳，直到拖曳锚达到受力平衡位置。

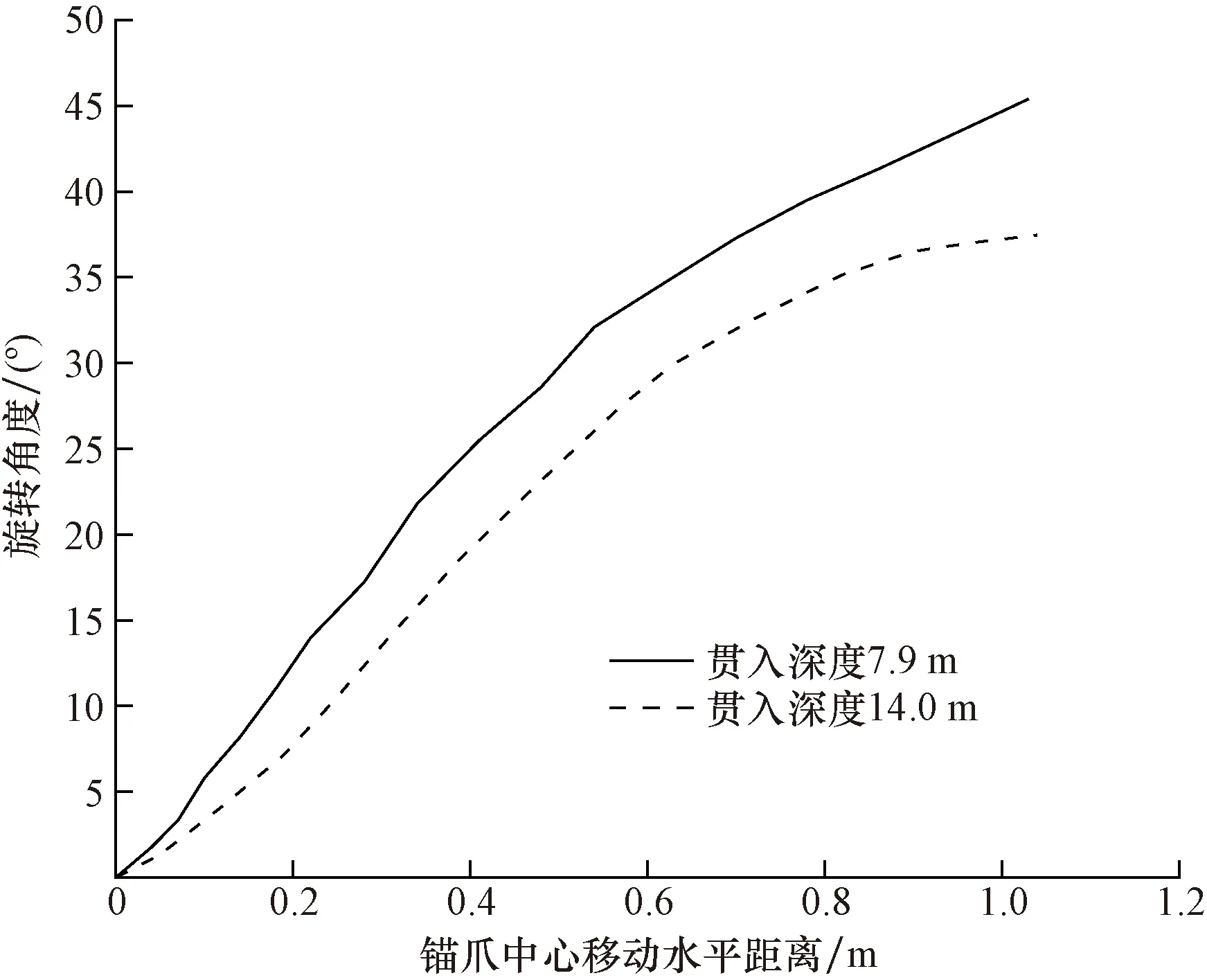
图7 拖曳锚系泊点位置变化 Fig.7 The change of mooring position with dragging distance

锚爪位置变化是由于系泊点拉力引起的，锚爪中心位置水平位移随系泊点拉力的变化如图8所示。可以看出，对于埋深为7.9 m的拖曳锚，随着锚拉力的增加，锚爪中心位置的水平位移也会不断增加，且增长趋势并没有随着锚拉力的增加而变缓，说明有走锚可能性；对于埋深为14 m的拖曳锚，当锚爪力达到19 000 kN时，锚爪中心位置的水平位移趋于平稳，说明其可以承受20 000 kN的拉力。由此可以看到贯入深度为确定拖曳锚承载力的关键因素。

图8 拖曳锚系泊拉力随位移变化Fig.8 The change of mooring loading with mooring position

4 拖曳锚设计计算流程

计算结果表明，选择40 t拖曳锚存在一定风险。重复上述步骤，对50 t MK6拖曳锚进行计算，不同计算方法得到的计算结果显示，50 t MK6拖曳锚可满足设计要求。

根据以上计算结果，建议采用如下流程进行拖曳锚的选择，如图9所示。

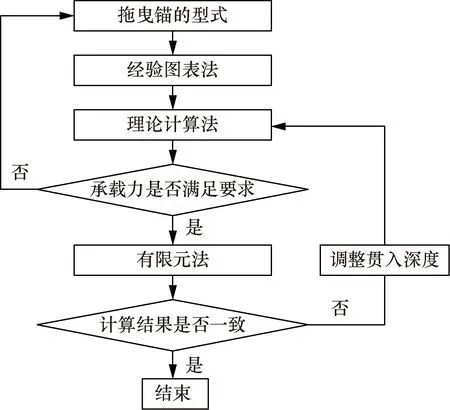
图9 拖曳锚选择流程Fig.9 The selection flow for drag embedded anchor

5 结论

总结了目前海上浮式风电锚固基础的使用情况，以Hywind场地条件为背景，对黏土场地拖曳锚承载力各种计算方法进行了评价，并得到如下结论。

(1) 相比于其他形式的锚固基础，拖曳锚由于其建造和安装成本较低，在浮式风电工程中具有较好的应用前景。

(2) 以Hywind风场为工程背景，利用不同方法计算了拖曳锚在均质以及强度随深度增加的黏土条件下的承载力。计算结果显示，拖曳锚的设计计算对土体强度的变化较为敏感，在两种不同土质条件下，贯入深度范围内的土体强度的平均值均为30 kPa，但其贯入深度和最终承载力相差达到70%。

(3) 对于强度随深度变化的土体条件，拖曳锚的贯入深度明显大于均质强度的土体。制造厂商提供的数据仅可作为初始承载力的估算使用，拖曳锚在具体场地的承载力需要更加详细的计算。

(4) 有限元分析结果显示，拖曳锚贯入深度为确定拖曳锚承载力的关键因素。如果将拖曳锚应用于浮式风电永久性锚固，需要对拖曳锚贯入过程进行更加深入的研究。