基于零知识证明的匿名投票方案
于筌,刘晓彤,刁恩虎,刘秀磊*
(1.北京信息科技大学北京材料基因工程高精尖创新中心,北京 100101; 2.北京信息科技大学数据与科学情报分析研究所,北京 100101)
电子投票是互联网时代常用的决策手段,第一个电子投票协议由Chaum[1]在1981年提出,该协议使用公钥密码学技术,解决了不可信通信环境下的投票安全问题。现有的大多数电子投票方案均依托于中心化节点,使用诸如盲签名[2]等密码学技术对投票过程进行加密。中心化架构具有系统结构简洁、响应速度快等特点,但同时也存在诸多不足。从系统需求的角度,中心化系统易被单点攻击,公信力不强;从加密算法的角度,中心化系统所基于的各种密码学算法限制了系统的构建:基于盲签名的电子投票系统[3]无法完全隐藏投票者身份信息;基于秘密共享的电子投票系统[4]通信复杂度较高[5];基于混合网络的电子投票系统[6]虽然可以完成匿名投票,但需要多个混合服务器,系统成本较高。
以太坊(Ethereum)[7]和零知识证明(zero knowledge proof)[8]技术的出现为这些缺陷提供了解决办法。以太坊是去中心化系统的代表,它的数据分布于全球矿工节点,智能合约在以太坊上基于共识机制运行,具有透明性和可信性。所有矿工节点保存着一份公认的合约执行结果,因此在区块链上运行的智能合约结果具有不可篡改性。现有很多系统选择使用区块链作为其底层结构来提升安全性,如基于区块链技术的数据共享系统[9]、基于联盟区块链的水产养殖品质量追溯系统等[10]。在电子投票领域,基于区块链的一个典型应用是当前实现在链上的各种不具备匿名性的去中心化自治组织(decentralized autonomous organization,DAO),其通过智能合约运转,具有较高的透明度和投票参与率,是未来区块链发展的重要方向。零知识证明由Goldwasser等[8]在1985年提出,旨在让证明者可以在不为验证者提供任何有用信息的情况下,使验证者相信某个论断正确。将零知识证明应用于链上的投票系统,可使投票者在不透露任何身份信息的前提下完成投票。
现从基本的非匿名智能合约链上投票系统出发,使用零知识证明技术对智能合约进行改进,以满足可重复匿名投票与不可重复匿名投票的应用场景,弥补原始链上投票系统的缺陷,使最终投票系统同时具备匿名性与不可伪造性。上述系统除满足常见投票场景外,亦可满足涉及隐私的问卷调查场景,进一步彰显本系统的价值。所有智能合约、合约部署步骤及相关交互代码均已开源,期望能为相关系统开发人员提供有益的参考。
1 相关技术
1.1 椭圆曲线密码
椭圆曲线密码 (elliptic curve cryptography)[11]是指利用椭圆曲线的特性来实现如公钥加密、共享密钥等技术的统称。与其他密码算法相比,其优势在于相同长度下密码强度高。由美国国家标准与技术研究院(National Institute of Standards and Technology,NIST) SP800-57文件[12]可知,长度250 bit左右的椭圆曲线密码与长度为2 048 bit的RSA(Rivest-Shamir-Adleman)密码具有近似的强度。使用对零知识证明电路设计友好的椭圆曲线Baby Jubjub[13]加密投票者身份信息,以保证投票方案的匿名性。
1.2 单向散列函数
单向散列函数是指可以将消息映射到散列值的函数,常见散列函数有SHA-256[14]、RIPEMD-160[15]、皮特森哈希(Pedersen Hash)[16]等。它需满足以下3种性质:抗碰撞性、隐秘性和谜题友好性。抗碰撞性是指函数难以人为产生哈希碰撞;隐秘性是指函数只能单向计算;谜题友好性是指函数输出值不可预测。为满足投票的实时性,选择使用电路精简、运行速度快的皮特森哈希。皮特森哈希的生成过程如下。
(1)对域名分隔符、数组[0,1,…,63]使用blake2s-256散列函数[17]生成散列值,再将散列值使用映射函数在Baby Jubjub曲线上映射生成64个点[G0,G1,…,G63]。
(2)将输入的位数用0填充至3的倍数。
(3)按照每块189 bit分块。
(4)再将每块按照每片3 bit分片,共63片。
(5)每片使用式(1)进行计算,其中mj代表此块中的第j片,s0、s1、s2分别为第j片的第1、2、3位。
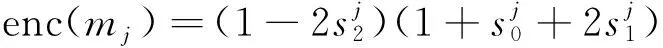
(1)
(6)将每片结果再乘以24j。
(7)所有结果相加得到H。
(8)计算[HG0,HG1,…,HG63],得到[P0,P1,…,P63]。
(9)计算P0+P1+…+P63,得到皮特森哈希基点。
(10)对皮特森哈希基点进行哈希抽取,抽取其x值作为最终皮特森哈希值。
1.3 非交互式零知识证明
非交互式零知识证明(non-interactive zero knowledge proof)[18]是一种特殊的零知识证明,证明者可以在不与验证者交互的情况下生成证明,以此排除证明者与验证者串通的情况。由于非交互式零知识证明协议允许智能合约充当验证者,因此非常适用于以太坊应用程序。在这种情况下,任何人都可以生成证据并将证据作为交易的一部分发送给智能合约,智能合约对证据进行验证后,根据结果执行后续操作。
最常用的非交互式零知识证明协议是简洁的非交互式零知识证明(zero-knowledge succinct non-interactive argument of knowledge,zk-SNARK)[19]。它是具有简洁证明和次线性验证时间的非交互式零知识协议,因其较高的可编程性而被大多数以太坊开发人员所接受。
在众多zk-SNARK算法中,Ronald Mannak对比了8种主流的zk-SNARK算法的性能参数[20],Fractal[21]、Halo[22]、SuperSonic[23]、Plonk[24]、Marlin[25]、Sonic[26]、Groth16[27]、zk-STARK[28]。研究表明,在证明数据量大小和验证速度方面,Groth16远好于其余算法[20]。因此使用Groth16算法作为系统核心算法,以达到减少投票成本、提升投票速度的目的。
2 基于智能合约的投票系统
基于智能合约的投票系统结构如图1所示,系统由链上智能合约与前端用户交互界面组成。智能合约负责提供基本投票功能、存储投票结果,并将投票过程标识为相应事件,以便用户从以太坊区块中查看。前端交互界面部分通过MetaMask浏览器钱包插件与链上智能合约进行交互。系统具体投票步骤如下。

实线箭头代表函数调用;虚线箭头代表数据传输图1 基于智能合约的投票系统结构Fig.1 The architecture of the voting system based on smart contracts
(1)用户连接MetaMask钱包,通过前端页面访问智能合约。
(2)智能合约使用权限函数通过访问者地址对访问者身份进行认证。
(3)认证通过后,用户调用功能函数进行投票。
(4)待投票结束后,合约返回投票结果至前端,以供用户查看。
3 基于零知识证明的匿名投票方案
上述实现的投票系统虽然通过地址对访问者身份进行了判断,在一定程度上保证了投票过程的安全性,但这种验证方式并不具备匿名性。在这种地址与投票权一一绑定的验证方式中,攻击者可以对地址的交易信息进行分析,构建用户画像,进而获取投票者部分身份信息。为了避免投票者身份信息泄露,系统需选择一种可以完全隐藏身份信息的方法。首先,采用数字签名技术标识投票者,将用于数字签名的公私钥称为投票私钥Pr和投票公钥Pb,以链下形式分发;其次,使用零知识证明技术隐藏Pr与Pb之间的关系,从而达到匿名投票的目的。
由于零知识证明方法会完全隐藏投票者特有信息,因此该方案无法满足不可重复投票的应用场景。为提高其通用性,在方案中加入皮特森哈希作为投票者的特征信息。智能合约可通过投票者发送的Pr的皮特森哈希来记录每个投票者的投票次数,以消除恶意投票者对投票过程的影响。引入的皮特森哈希既与Pb无直接关系,又可以保护Pr,使该方案满足匿名性的同时提高了通用性。
图2所示的匿名投票方案的具体运行流程分为5个阶段,分别为准备阶段、发布投票阶段、投票阶段、验证阶段和计票阶段。下面将对每个阶段的算法进行介绍,其中表1记录了算法中用到的主要参数及其代表符号。
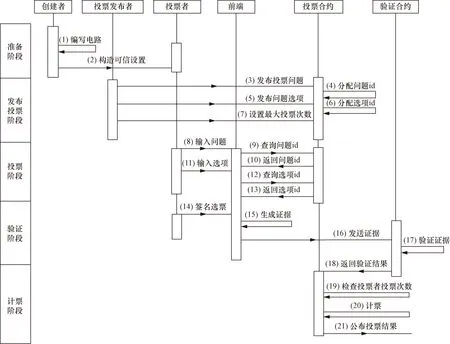
图2 匿名投票方案运行流程Fig.2 Anonymous voting scheme operation process

表1 主要参数Table 1 Primary parameters
3.1 准备阶段
系统准备阶段共分为两个部分,编写零知识证明算术电路和构造可信设置,对应图2中的步骤1、步骤2。
方案创建者首先需编写零知识证明算术电路。电路描述构造和验证零知识证明证据时需遵循的约束规则,其输入分为私有输入与公有输入。 私有输入包括所有证明者想要证明的秘密,对验证合约不可见;公有输入包含私钥哈希、投票者投票选择等投票信息,对验证合约可见。
算法1:零知识证明算术电路。
私有输入:Pr,R;
公共输入:PbG,H′,R′;
Pb= GenPublicKey(Pr);
(2)fori= 1,2,3,…,len(PbG) do:
(3)/*约束投票公钥必须在投票公钥组中*/
PbG[i]=Pb;
(4)end for
H= GenHash(Pr) ;
(6)/*约束投票私钥的哈希与合约接收的投票私钥哈希一致*/

(7)/*约束投票选择与合约接收的投票选择一致*/

构造可信设置即使用算术电路生成用于进行零知识证明的两组随机数:Pk和Vk。随后方案用得到的Pk和Vk生成验证合约,验证合约用于在验证阶段对智能合约的访问者进行身份验证。
3.2 投票发布阶段
在投票发布阶段,投票发布者会发布投票问题和相应选项至投票合约,并设置每个投票者最大投票次数。投票发布阶段算法如算法2所示,对应图2的步骤(3)~步骤(7)。
算法2:投票发布算法。
输入:Vq,Vo,Vmax;
输出:Qi,Oi;
(1)PsendVqtoSt;
(2)StassignQitoVq;
(3)returnQitoP;
(4)fori= 1,2,3,…,do:
(5)Psend (Vo,Qi) toSt;
(6)end for
(7)StassignOitoVo;
(8)returnOitoP;
(9)PsendVmaxtoSt;
(10)StsaveVmax;
3.3 投票阶段
在投票阶段,投票者将其选择输入前端,前端与合约交互得到相应问题与选项的id,以便在验证阶段完成电路约束,生成证据。投票算法如算法3所示,对应图2的步骤(8)~步骤(13)。
算法3:投票算法。
输入:Vq,Vo;
输出:R;
VrequireQifromSt;
returnQitoV;
VrequireOifromSt;
returnOitoV;
R=[Qi,Oi];
3.4 验证阶段
在验证阶段,验证合约验证访问者是否拥有投票权限。投票者需要对投票选择进行签名,前端根据其投票私钥生成证据,并将证据、投票私钥哈希和在投票阶段获得的相应id发送给验证合约。验证合约根据证据检查投票者身份和投票选择的正确性。验证阶段算法如算法4所示,对应图2的步骤(14)~步骤(18)。
算法4:验证算法。
输入:Pr,PbG,R;
(1)H= GenHash(Pr);
(2)Ci=[Pr,PbG,H,R];
(3)W= Calculate Witness(Ci);
(4)Pi= Slice(W);
(5)/*使用见证和证明密钥生成证据*/
π= Prove(W,Pk);
(6)/*投票者发送证据到验证合约*/
VsendπtoSv;
(7)/*验证合约验证访问者身份*/
if Verify(π,Pi):
(8)SvsendR′ toSt;
(9) else
(10) visitor is not a voter;
(11)end if
3.5 计票阶段
当访问用户被确定是投票者后,验证合约将信息发送给投票合约,方案进入计票阶段。在计票阶段,投票合约需先验证投票者的投票次数是否符合规范。如果符合,则将投票计入;否则,将投票作废。投票结束后,投票合约根据投票选择将得票最多的选项设置为最终投票结果。计票阶段算法如算法5所示,对应图2的步骤(19)~步骤(21)。
算法5:计票算法。
(1) ifH′ not in HL:
(2) PutH′ in HL;
(3) else:
(4) ifVc (5) vaild vote; (6) else: (7) invaild vote; (8) end if (9) end if (10) after voting: (11)Stcalculate final results; (12) return final results; 提出的匿名投票方案不仅满足Fujioka等[29]在1992年提出的电子投票系统应具有的7种基本安全性质:合格性、匿名性、不可重复性、完整性、正确性、公平性和可验证性,还满足稳定性和通用性。 4.1.1 合格性 合格性指没有投票权的用户无法进行投票。在本文方案中,验证合约需要根据访问者提交的证据验证访问者的身份,给予其相应的投票权限。只有拥有投票私钥的投票者能生成正确的证据,执行投票操作,因此方案满足合格性。 4.1.2 匿名性 匿名性指所有投票者信息应被保密。本文方案分两步完成投票匿名性。第一步,方案使用数字签名和零知识证明技术解除了投票权对地址的依赖,使投票者可以通过任意以太坊地址进行投票,消除了投票者真实以太坊地址暴露的隐患。第二步,方案用于与链上合约交互的数据和合约中保存的数据均不包含任何投票者身份信息,防止攻击者通过合约窃取投票者相关信息。至此方案满足匿名性。 4.1.3 唯一性 唯一性指投票者在某些场景下不可重复投票。本文方案采用投票私钥哈希作为特有信息标识投票者。在不可重复的投票场景中,投票合约可以通过此标识判断投票者投票情况。因此方案满足唯一性。 4.1.4 完整性 完整性指所有有效选票都被正确计算。对方案验证阶段和计票阶段的投票完整性进行分析。在验证阶段,方案使用零知识证明技术约束投票者的投票选择无法被篡改。在计票阶段,因智能合约具有原子性,投票合约接收的正确的投票选择一定会按照规定好的投票规则计入结果。因此方案满足完整性。 4.1.5 正确性 正确性指所有无效选票都不被计算。本文方案共有两种出现无效选票的场景,一种是投票者投票次数超出投票发布者规定的最大投票次数,另一种是攻击者篡改投票者正确的投票选择后生成伪造选票。 针对第一种场景,方案在验证阶段通过检查投票者的投票次数对其进行甄别。针对第二种场景,由于伪造选票不满足零知识证明算术电路的约束,因此其无法通过验证合约的检测。至此两种无效选票均无法计入投票结果,方案满足正确性。 4.1.6 公平性 公平性指投票中间结果不可被获取。本文方案虽然在投票结束前不会公布投票结果,但每个投票者的投票选择会伴随交易记录保存在以太坊中。由于投票选择采用明文传输,攻击者可以通过交易记录中的数据计算出中间投票结果。针对上述场景,方案可通过合理设置投票时间来避免中间投票结果泄露,满足公平性。 4.1.7 可验证性 可验证性指投票结果不会被伪造。本文方案在以太坊上运行,投票过程的每一步和投票结果都通过交易记录和事件日志被记录在以太坊分布全球的节点中,具有不可篡改性。因此投票结果与投票过程均不可篡改,方案满足可验证性。 4.1.8 稳定性 稳定性指系统抗干扰的能力。本文方案是去中心化的投票方案。方案不会因节点故障等中心化系统常出现的问题,造成投票数据丢失、投票系统崩溃等严重后果,因此方案稳定性较强。 4.1.9 通用性 通用性指系统适用于不同应用场景的能力。本文方案可同时满足可重复匿名投票和不可重复匿名投票两种投票场景,且支持投票发布者根据自身需求设置每个投票者的最大投票次数,具有良好的通用性。 通过将本文方案与已提出的电子投票方案进行对比分析(表2),表明本文方案基本解决了电子投票系统常见的安全问题。 表2 方案对比Table 2 Comparison of schemes 文献[30]提出的投票方案虽然在文献[29]提出的方案上进行改进,解决了选票碰撞问题,增强了方案的安全性。但其仍然是中心化投票方案,严重依赖可信第三方,因此不满足投票匿名性、可验证性和稳定性。文献[31]和文献[32]提出的电子投票方案将保存的以太坊地址作为投票者特有信息来验证投票唯一性。与第3节描述的方案相同,这种方式限制投票者只能使用特定的以太坊地址进行投票,虽然没有直接暴露投票者身份信息,但攻击者可以由此得到投票者真实以太坊地址,进而获取投票者真实身份信息,方案不满足匿名性。文献[30-32]提出的电子投票方案虽然分别使用可信第三方分配的身份标识和以太坊地址作为投票者特有信息对投票唯一性进行判定,但3种方案均未考虑可重复投票场景,不满足通用性。文献[33]中提出的方案使用一次性环签名算法,满足电子投票系统的基本安全要求。但方案无法同时满足可重复投票和不可重复投票场景,通用性差于本文提出方案。和上述3种方案相比,本文方案满足电子投票方案应具有的安全特性,且具备更好的通用性,可以满足各种不同的应用场景。 提出一种结合零知识证明与数字签名技术的链上匿名投票方案。该方案可以使投票者在不暴露任何身份信息的前提下完成投票,并通过算术电路来约束投票过程的完整性和正确性。借助以太坊去中心化、透明、不可篡改等特点,实现了投票可验证性和系统稳定性。经过对比分析,方案在满足电子投票系统基本安全特性的同时,还具备比已提出的电子投票系统更好的通用性,适用于不同的应用场景。4 方案分析
4.1 安全性分析
4.2 方案对比分析

5 结论

