主动配电网下分布式能源系统双层两阶段调度优化模型
袁天梦,侯鑫垚,廉杰
(国网冀北电力有限公司唐山供电公司,唐山 063000)
随着能源全球化进程的不断推进,高效、清洁、多样化的现代能源系统逐渐成为中国能源发展转型的主要途径。当今世界多数国家均使用大功率的单一供电系统为电力用户提供能源,这种集中式供电方式为95%左右的用户提供服务。随着电力用户的逐渐增加,如何保证能源供应与安全,提高能源利用率,降低污染物排放成为电力系统发展过程中急需解决的问题[1-2]。针对上述问题,能源互联网应运而生,此网络中不仅包含多种能源单元,更能满足用户的多元化应用需求,为集中式供电方式提供强有力的能源保证。分布式能源系统是能源互联网中的重要组成部分,可为区域性配电网的能源提供供给[3]。分布式能源系统的发展不仅提高了清洁能源的利用率,更为中国电力事业与环保事业的发展提供了帮助。
国内外一些学者对此展开了研究,王永利等[4]提出了一种考虑需求响应的分布式能源系统多能协同与储能规划方法,通过建立由风机、光伏、热电联产和电锅炉、储能系统组成的综合能源系统多能协同模型,通过规划各设备容量情况,满足电热负荷需求,并采用遗传算法对该规划方案进行优化。易灵芝等[5]提出了一种含微电网群的主动配电网双层联合优化调度方法,上层模型主要是以配电网为研究对象,应用遗传算法来降低配电网线损,提高电能质量;下层模型主要是以微电网为研究对象,应用混合整数线性规划来降低运行成本。张学军等[6]提出了一种含风储联合单元的电力系统两阶段日前调度模型,针对电力市场环境下含风储联合单元的电力系统日前调度问题,建立了两阶段调度优化模型。第一阶段主要是以风储联合单元的期望收益最大为目标,对日前投标量进行优化;第二阶段主要是以系统综合运行成本最小为目标,对日前机组组合进行优化。王子驰等[7]提出了一种基于多能互补分布式能源与综合能源管理系统优化调度方法,通过构建某一区域的多能互补分布式能源系统,采用负荷预测的方法进行系统的优化,实现系统调度的最大经济效益。刘华等[8]提出了一种天然气冷热电联供分布式能源系统优化调度方法,基于改进粒子群算法,提出天然气冷热电联供系统中各设备的优化调度模型,并对设备运行进行条件约束,确保运行成本最低。以上方法都可以进行分布式能源调度,并且可进行多角度调度。但在主动配电网下的分布式能源系统双层两阶段调度中,优化模型分层调度能力不高,使得能源利用率不高。
为解决以上方法在主动配电网下的分布式能源系统双层两阶段调度中的问题,在考虑能源利用率和运行成本的基础上,现构建一种主动配电网下分布式能源系统双层两阶段调度优化模型。首先,构建主动配电网双层能量管理下分布式能源系统日前与日内两阶段调度模型,并以提高能源系统的利用率作为目标函数,设定双层两阶段调度优化模型的约束条件,控制能源系统的调度过程。其次,使用帝国竞争优化算法对能源系统调度优化模型进行求解,获取最佳调度方案。最后,构建算例分析环节,将该模型和算法引入IEEE-33节点配电网中,进行测试,验证所提模型的有效性。
1 调度优化模型构建与求解
1.1 主动配电网下分布式能源系统双层两阶段调度优化模型构建
主动配电网下分布式能源系统调度优化的目的是在确保配电网稳定运行的前提下,使可再生能源能够得到最大化利用,系统的总体运行成本最低。由于传统方法下的优化模型对于日前与日内两阶段模型构建结果较好,但模型分层效果不佳[9-10]。因此,将优化模型构建为上、下两层,上层负责节点功率的调度,以网损最小为目标,进行全局优化,下层以运行总成本最低为目标,局部优化[11-12]。在调度的过程中考虑日前与日内两个阶段的能源系统作用与表现,优化模型可表示为
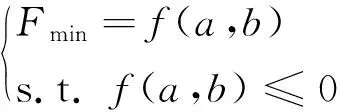
(1)
式(1)中:b为下层调度变量;a为上层调度变量;f(a,b)为目标函数。
根据式(1)可得到a、b为指定数据时,调度的最优解为
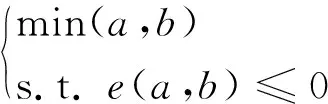
(2)
已知上层目标函数为满足多种约束条件的能源系统运行成本,在研究中,将分布式能源系统中的微型燃气轮机运行成本作为主要研究对象。通过文献[13-14]分析可知,能源系统供能具有时段性,为保证此系统的正常运转,需在其中安装相应的负荷稳定器,则此电源的运行成本Fl可表示为
Fl=ui(Pi)2+viPi+si
(3)
式(3)中:ui、vi和si为燃料费用系数;Pi为微型燃气轮机组正常运行功率。
除此成本外,风电机组与光伏机组不计入燃料成本,其发电成本函数可使用Ji、Ki表示,则有
Ji=PjiRJ
(4)
Ki=PkiRK
(5)
式中:Pji、RJ分别为风电机组的有效出力与维护费用;Pki、RK分别为光伏机组的有效出力与维护费用。将上述计算内容融入当前上层目标函数中。
在下层调度模型的构建过程中,需对系统中的各个电源分配情况进行分析,以提高能源系统的利用率作为目标函数。则此目标函数[15]可表示为
minOz=αiOi+αjOj
(6)
式(6)中:Oi为调度过程中,能源系统的总网损函数;Oj为能源系统中各电压节点偏移函数;αi与αj分别为上述两系数在下层调度函数中的权重系数。
为保证上下层目标函数具有科学性,将其约束条件设定如下。
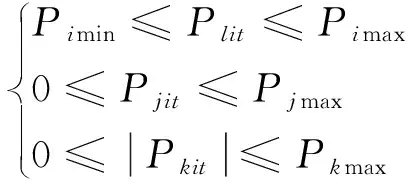
(7)
式(7)中:Pimin为微型燃气轮机组i的出力下限;Pjmax、Pkmax分别对应能源系统中的风电机组与光伏机组的出力上限。
将上述公式作为双层两阶段调度优化模型的约束条件,控制能源系统的调度过程。
1.2 主动配电网下分布式能源系统双层两阶段调度优化方案求解
使用差分帝国竞争算法对构建的调度优化模型进行求解。在此算法的使用过程中,其最小的个体单位是国家[16],根据相应计算原理,可将国家视作N×1的矩阵,则有
c=[d1,d2,…,dn]
(8)
根据以往研究结果,将国家的价值与势力通过代价函数体现,则有
cost=f(c)=f(d1,d2,…,dn)
(9)
在模型求解的过程中,寻找分布式能源系统运行的最小成本。在计算前,需给定初始化的国家数量ncou以及原始帝国数量nemp。经过多次计算得到初始国家后,选择初始国家nemp中代价函数的取值最小但力量最强大的国家作为初始化帝国主义国家,剩余数据作为此部分帝国主义国家的殖民地。
每个国家对应的殖民地个数的具体计算过程如下。
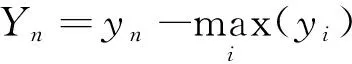
(10)
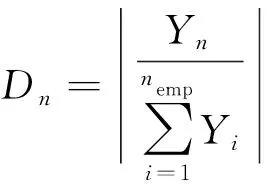
(11)
N(Yn)=round{dn,N}
(12)
式中:yn为第n个帝国类型国家的代价函数取值。
使用式(10)将其转化为标准代价取值结果,而后再将标准代价取值结果代入式(11)中,得到各个国家的势力大小标准值dn。最后,使用式(12)得到各个国家的初始殖民地个数。在分布式能源系统的调度过程中,更具有优势的方案会通过整合较差的调度方案提高此方法的使用效果[17],在帝国竞争算法中通过竞争机制模拟此过程。在研究中,帝国的总成本表达式为
U(Yn)=f(empn)+φmean[f(cempn)]
(13)
式(13)中:第n个帝国的总代价使用U(Yn)表示,帝国总体势力与殖民地之间的关系通过φ体现。通过计算可知,当φ取值越大时,两者之间更易出现相互影响的情况,但其整体取值范围控制在(0,1)。每个帝国都希望通过殖民掠夺扩大版图,并控制其他的国家。在此行为开始后,较弱的帝国会成为竞争计算的核心,则每个帝国被占领的可能性可表示为
NU(Yn)=U(Yn)-max[U(Yi)]
(14)
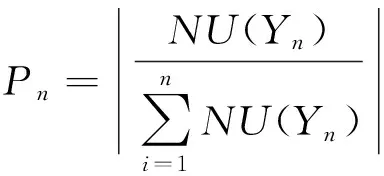
(15)
式中:U(Yn)与NU(Yn)分别为第n个国家的代价函数以及代价函数标准值;Pn为此帝国成为势力最弱帝国的可能性。
在帝国互相竞争侵占的过程中,势必会出现帝国大量消亡的情况[18]。与此同时,殖民地的数量将会随着计算迭代次数不断减少。当大部分帝国均消失后,所剩下的最强帝国所代表的方案,则为本次调度优化模型的最优解。其所侵占的殖民地位置将会收敛于帝国位置的周围。
2 算例测试分析
完成了新型分布式能源系统双层两阶段调度优化模型的构建过程后,为验证模型具有一定的使用效果。在理论部分设计完成后,构建算例测试分析环节,对此模型的应用结果与性能加以分析。
2.1 算例参数设定
对比多个案例后,选择IEEE-33节点配电网测试系统搭建测试环境,使用仿真实验的方式得到模型应用结果。此系统拓扑结构为辐射状三相平衡系统。根据算例测试要求,将系统电压设定为11 V,可承载有功负荷阈值设定为3 000 kW,可承载无功负荷设定为2 000 kVar,测试系统基本结构如图1所示。
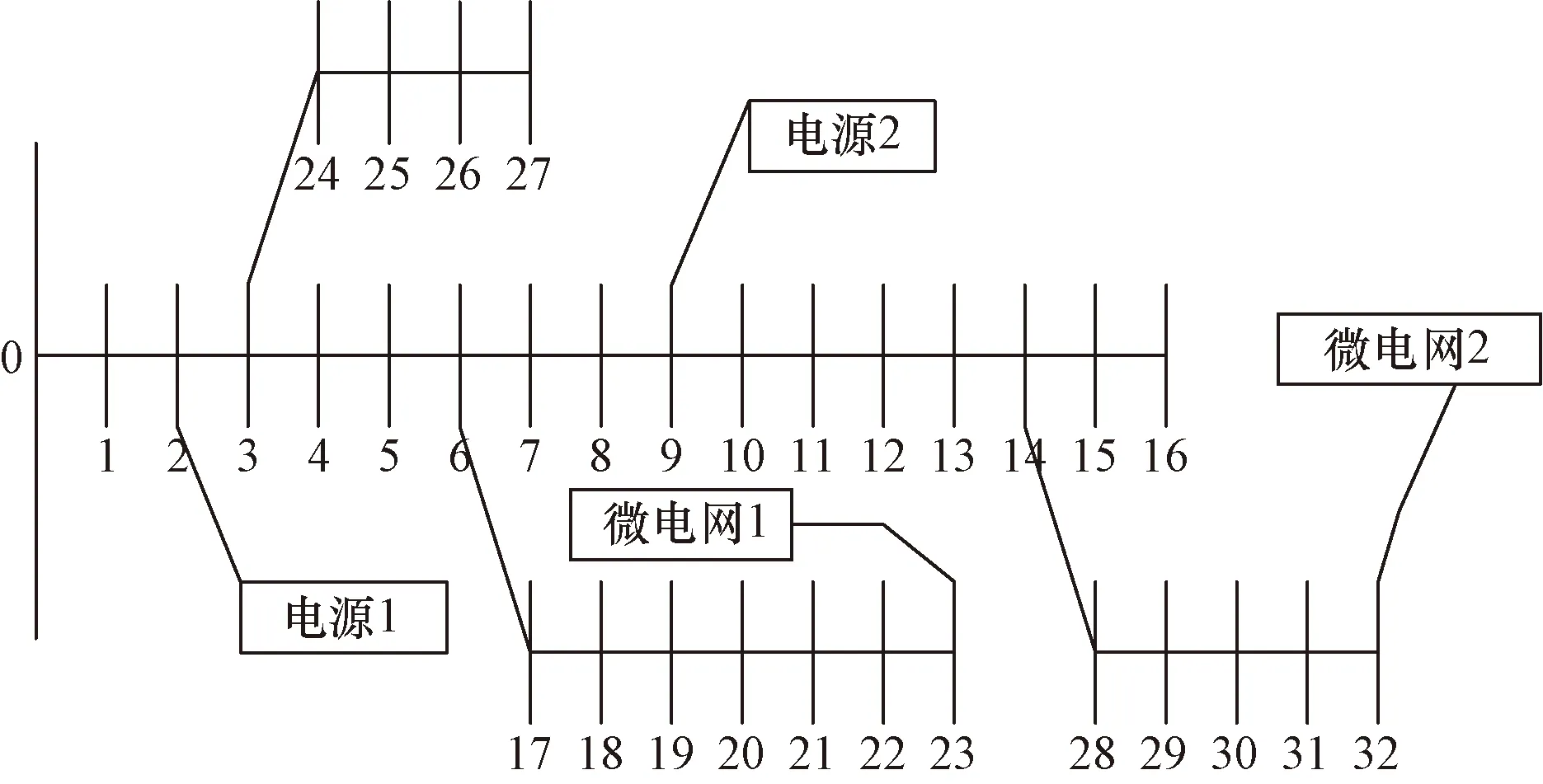
节点0为变电站节点,其余节点为工作节点图1 IEEE-33节点配电网测试系统结构图Fig.1 IEEE-33 node distribution network test system structure diagram
为使其更加贴近真实主动配电网应用环境,将电源分别接入节点9与节点2,微型电网安装在节点32与节点23的位置。选用微型燃气轮机作为分布式电源,此电源额定功率为300 kW。引入系统中的微电网中包含燃气轮机、光伏设备以及风力机组。所研究的配电测试系统各支路的年最大负荷利用时间Tmax=150 h,单位售电价格ci=1.0元/(kW·h),能源系统规划年限设定为5年。此外,为提升算例的真实性,在本次测试中主要考虑日前与日内两种优化调度模式。在算例测试中将上述设定结果作为测试的基础,以此分析优化模型的使用效果。
2.2 算例数据设定
引入MATLAB软件中的3次样条差值法,为算例分析提供数据基础。在测试前,获取日前24 h调度计划,将日前24 h划分为96个数据点,每个单位时间周期设定为15 min,则采样时间间隔可表示为t=15 min。日内调度时间周期与优化时域均设定为10 min,则日内采样时间间隔可表示为t=5 min。与此同时,将此测试系统各节点参数设定如表1所示。
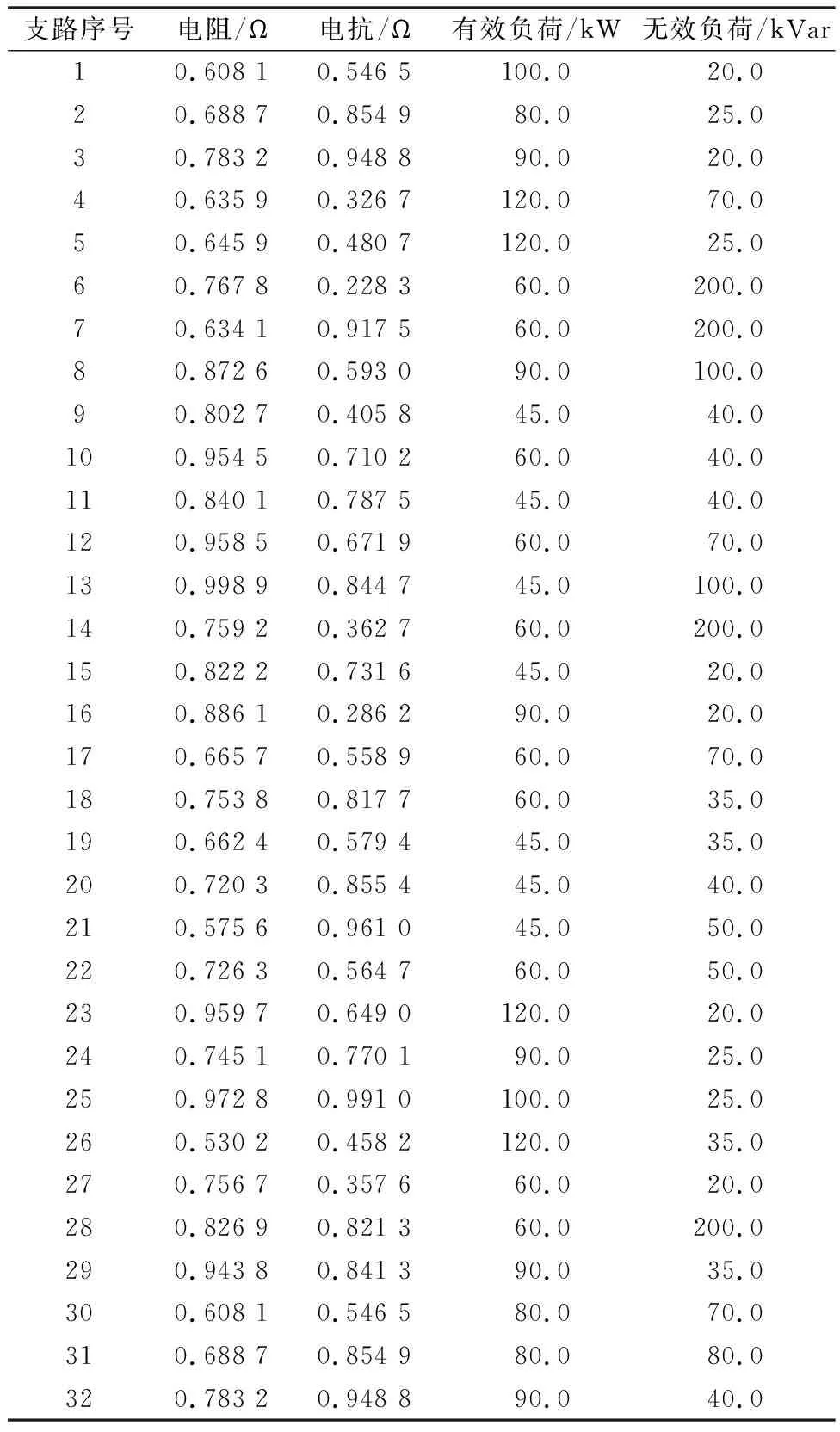
表1 IEEE-33节点配电网测试系统相关参数设定结果Table 1 Parameter setting results of IEEE-33 node distribution network test system
除上述数据外,将光伏发电成本设定为0.015 0元/(kW·h);风力发电成本设定为0.005 8元/(kW·h);微电网发电成本为0.041 50元/(kW·h);微型燃气轮发电成本为0.005 14 元/(kW·h)。将此部分数据作为算例测试中的初始成本参数,使用此参数辅助完成计算过程,并对不同调度方法应用前后的成本变化加以分析。
2.3 所提方法调度前功率测试结果及分析
根据算例设定结果,得到分布式能源系统日前调度结果,如图2所示。

图2 所提方法应用前功率测试结果Fig.2 Power test results before application of the proposed method
根据图2的曲线变化趋势可知,在0:00—6:00,整个分布式能源系统处于充电状态,此时段内能源系统中的储能容量较低,各功率值均较低,系统中的剩余功率将通过联通线路传输到系统的储能单元,为后期的电能需求高峰期提供供给保障。在12:00左右,逐渐达到用电高峰期,配电网的功率大幅度提升,使用提出的调度优化模型可以很好地实现功率的消纳,并充分利用此部分能量完成其他工作项目。
2.4 所提方法调度后功率测试结果及分析
根据已设定的算例参数以及数据,得到主动配电网分布式能源系统日内调度结果,具体如图3所示。
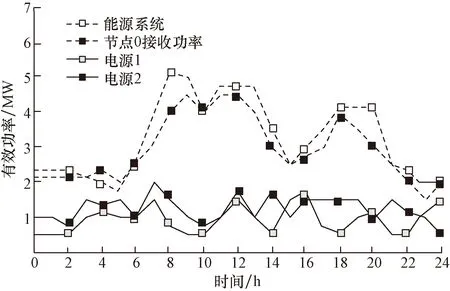
图3 所提方法应用后功率测试结果Fig.3 Power test results after application of the proposed method
根据图3可知,所提方法应用后功率总和得以下降。由此数据进行分析可知,日内调度在一定程度上缩小了全天电力需求的最大值与最小值之间的差距,使得能源系统电能输出更加稳定。与此同时,对燃气轮机的有效出力进行计算可知,其出力大小发生了明显的变化,比照日前调整阶段同比增长了1.5%。由此可知分布式电源的出力大小均发生了较大的变化,其利用率得到了明显的提升。
2.5 方法应用前后的成本对比
为了突出本文方法的实用性,对比所提方法应用前和应用后的光伏发电成本、风力发电成本、微电网发电成本、微型燃气轮发电成本。根据实验初始参数设置可知,单位功率对应的光伏发电成本设定为0.015 0元/(kW·h);风力发电成本设定为0.005 8元/(kW·h);微电网发电成本为0.041 50元/(kW·h);微型燃气轮发电成本为0.005 14 元/(kW·h)。成本的具体对比结果如表2所示。
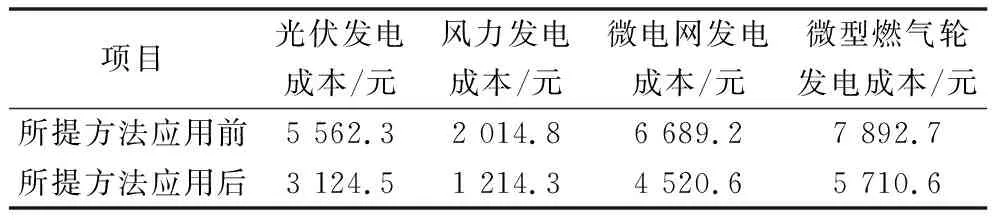
表2 所提方法应用前后的成本对比Table 2 Cost comparison before and after application of the proposed method
根据表2可知,所提方法应用下,光伏发电成本、风力发电成本、微电网发电成本、微型燃气轮发电成本均明显下降,说明所提方法具有理想的实用性,优化主动配电脑网下分布式电源的应用效果和经济效益。
2.6 算例测试结果讨论
在当前分布式能源系统调度优化模型的基础上进行了研究,并提出了可分阶段分层调度的分布式能源系统调度优化模型。根据日前与日内两阶段调度结果以及其分析内容,确定研究中提出模型的使用效果。算例测试结果表明:此模型具有一定的使用价值,通过对目前阶段的研究可以确定,调度优化模型可提升分布式电源的利用率。与此同时,此模型使用后,分布式能源系统运行状态更加稳定。由此可知,此模型可降低分布式能源运行的波动性以及不确定性。综上所述,提出的新型调度优化模型具有较高的使用价值,可将其应用到实际的电力系统调度管理工作中。
3 结论
分布式能源系统的经济调度问题一直都是电力系统发展研究中的关键问题,其中合理的调度优化模型是降低电力系统运行成本和提升系统运行性能的关键,为此提出了双层两阶段调度模型。经算例测试证实,此调度优化模型具有较好的使用效果以及良好的应用前景。在以后的研究中可对模型的计算部分进行更为详细的分析,不断完善优化模型结果,提高模型使用效果。

