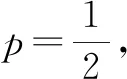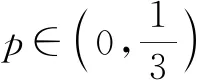概率统计与函数的交汇

⦿广州市增城区郑中钧中学 周晓霞

在新课标高考数学试卷中，概率统计是其中一大重要的主干知识，特别是其与函数的交汇应用问题，能很好地融入创新情境与交汇知识，实现不同主干知识之间的联系与转化，对于考查学生基础知识、基本能力与思想方法等有很好的效果，倍受命题者青睐.

1 利用二次函数处理概率统计问题

例1(多选题)设实数p满足0

表1

则当p在(0，1)内增大时( ).

A.E(ξ)减小

B.E(ξ)增大

C.D(ξ)先减小后增大

D.D(ξ)先增大后减小

点评：利用二次函数(或其他相关的函数类型)来解决概率统计问题时，关键是结合相应的概率统计要素构建起对应的函数，进而借助函数的图象或性质来解决一些相关的单调性、最值等应用问题.

2 利用基本初等函数处理概率统计问题

例2已知样本x1，x2，……，x2022的平均数和方差分别是1和4，若yi=axi+b(i=1，2，……，2022)的平均数和方差也分别是1和4，则ab=.

综上可知，ab=1.故答案为1.

点评：抓住一次函数所对应的平均数和方差与对应样本数据的函数关系式(分别是一次线性函数与二次函数)来构建对应的方程组，这是问题解决的关键与切入点，也是概率统计中相关概念的函数基本性质.熟练掌握概率统计中相关概念的函数基本性质等，也是函数概念与性质的深入与应用.

3 利用分段函数处理概率统计问题

例3某超市同一月按每天相同进货量订购一种品牌的酸奶，每瓶酸奶对应的进货成本与售价分别为5元与8元，未售出的酸奶当天晚上九点以后以每瓶3元的价格酬宾全部处理完.根据销售经验与当天的最高气温(单位：℃)数据信息，如果当天最高气温不低于30，需求量为500瓶；如果当天最高气温位于区间[25，30)，需求量为300瓶；如果当天最高气温低于25，需求量为200瓶.为了确定八月份的预订数目，统计了当地前三年八月份每天的最高气温数据信息，得如表2的频数分布表：

表2

假设以最高气温位于各区间的频率代替最高气温位于该区间的概率.

(1)试确定八月份这种酸奶一天的需求量X(单位：瓶)的分布列；

(2)若要求八月份一天销售这种酸奶的利润的数学期望值不低于700元，则八月份的每天的进货量n(单位：瓶)应满足什么条件？

解析：(1)根据题目条件，需求量X的所有可能取值为200，300，500.

因此所求的分布列如表3所示.

表3

(2)由(1)可知这种酸奶一天的需求量在200至500瓶之间，则只须考虑200≤n≤500，n∈Z.

当300

由E(Y1)≥700，解得n≤400，此时可得300

当200≤n≤300时，设酸奶利润为Y2，则E(Y2)=0.3[200×3-2(n-200)]+0.7×3n=1.5n+300.

综上可得，267≤n≤400,n∈Z.

点评：分段函数在概率统计的实际问题中应用比较广泛，结合概率统计问题中变量的不同分段取值情况，利用分段函数的本质，对应的概率统计要素也要对应地进行分类讨论，综合应用.

4 利用函数的导数处理概率统计问题

例4[2021年广东省梅州市平远中学高三(上)第五次段考数学试卷]高校的《博士硕士学位论文抽检办法》(教育部2014年印发)通知中规定：每篇抽检的学位论文送3位同行专家进行评议，3位专家中有2位以上(含2位)专家评议意见为“不合格”的学位论文，将认定为“存在问题学位论文”.有且仅有1位专家评议意见为“不合格”的学位论文，将再送另外2位同行专家(不同于前3位专家)进行复评，2位复评专家中1位以上(含1位)专家评议意见为“不合格”的学位论文，将认定为“存在问题学位论文”.设每篇学位论文被每位专家评议为“不合格”的概率均为p(0

(2)现拟定每篇抽检论文不需要复评与需要复评的评审费用分别为900元与1 500元，若某次评审抽检论文总数为3 000篇，求该次评审费用期望的最大值及对应p的值.

(2)设每篇学位论文的评审费为X元，则X的可能取值为900，1 500，于是

令函数g(p)=p(1-p)2，p∈(0，1)，求导可得g′(p)=(1-p)2-2p(1-p)=(3p-1)(p-1).

点评：在处理与解决实际应用问题中的概率统计变量时，对于一些高次函数等情况，经常可以通过构建对应的函数，结合高次函数的导函数来确定对应高次函数的单调性，由此确定该函数的极值或最值等相关问题，为实际应用与判断提供理论基础.

概率统计问题与函数的交汇应用问题，综合性较强，往往可以借助二次函数、基本初等函数或分段函数，利用函数的单调性解决与随机变量的数学期望、方差相关的最值问题；或借助导数研究函数的极值点，从而确定概率统计问题中的最优解来决策与应用等.这些概率统计与函数的交汇融合问题，其本质仍是以概率统计为主导进行问题情境创设，利用函数的性质或导数这一工具加以辅助求解或综合应用，实现基本数学知识之间的交汇融合，促进学生数学应用意识与数学创新能力的提升.