考虑剪切变形下隧道开挖引起邻近桩基水平向响应简化分析

冯国辉，郑茗旺，黄展军，侯世磊，徐长节,5,6，程康，葛尚奇，孙佳政，黄小彬

(1.浙江大学 滨海和城市岩土工程研究中心，浙江 杭州，310058；2.浙江大学 平衡建筑研究中心，浙江 杭州，310028；3.南昌轨道交通集团有限公司，江西 南昌，330013；4.中铁十四局集团 第四工程有限公司，山东 济南，250002；5.华东交通大学 江西省岩土工程基础设施安全与控制重点实验室，江西 南昌，330013；6.江西省地下空间技术开发工程研究中心，江西 南昌，330013；7.中铁十一局集团有限公司，湖北 武汉，430061；8.南昌市政公用工程项目管理有限公司，江西 南昌，330000)

随着城市经济的发展，城市地下空间的发展也越来越受到人们的青睐。这其中不乏存在隧道开挖对邻近建筑物的影响，例如隧道开挖引起邻近土体应力应变场发生改变，进而使得邻近桩基发生较大变形无法正常工作。因此，关于隧道开挖对邻近桩基的影响方面的研究也越来越受到众多学者的关注。

相比于有限元模拟[1-2]和室内实验[3-4]的方法，理论解析法可以简单快速预测邻近堆卸载对既有桩基变形响应。理论解析方法大多属于两阶段分析法，第一阶段通过LOGANATHAN等[5]提出能够准确估算隧道开挖引起周边土体位移计算公式；第二阶段把自由土体位移作为附加应力施加在既有桩基上，将桩基简化成不同的梁模型放置在不同的地基上，进一步获得桩基单元受力平衡方程，最后求解方程得到桩基应答响应。基于单参数Winkler 地基模型，李早等[6-7]将桩基简化成Euler-Bernoulli 梁搁置在Winkler 地基模型上，结合桩基两端自由的条件获得桩基变形响应差分解；梁发云等[8]引入最小势能原理获得Winkler 地基模型下既有桩基水平方向位移变形控制方程，随之解方程获得桩基变形解析解；LIANG等[9-10]基于弹性地基梁和Winkler地基模型，分别获得水平荷载作用下既有桩基承载力解析和桩基非线性变形响应变分解；可文海等[11]基于Euler-Bernoulli梁和Winkler地基模型，解析获得邻近隧道开挖对既有桩基的竖向变形响应。然而，Winkler 地基模型并未考虑到土体剪切变形对桩-土相互作用的影响，在预测桩基变形时存在较大误差。为了克服这一缺点，前人提出了能够考虑土体剪切变形的双参数Pasternak 和Ⅴlasov 地基模型，双参数地基模型在计算地下结构物与土体相互作用时具有良好的预测精度，因此被广泛使用[12-14]。冯国辉等[15]基于Winkler 和Pasternak 地基模型研究了隔离桩对盾构掘进对邻近高铁桩基的变形响应；梁发云等[16]基于Euler-Bernoulli梁Pasternak地基模型解析获得受荷被动桩水平向解析应答；ZHANG等[17]考虑到桩周侧向土体影响，基于Pasternak 地基模型提出了侧向土体影响下桩土相互作用解析应答。

为了更加准确预测隧道开挖引起邻近桩基的变形响应，KERR[18]提出了三参数Kerr 地基模型，杨涛等[19]基于Euler-Bernoulli 梁和Kerr 地基模型提出了邻近堆卸载对邻近桩基水平变形半解析解；ZHANG 等[20-21]利用Kerr 地基模型模拟桩-土相互作用，结合桩基两端自由的条件，获得桩基水平向变形解答。

综上所述，大部分桩土相互作用的理论研究均是将桩基简化成Euler-Bernoulli梁搁置在Winkler和Pasternak 地基模型上，忽略了桩基自身剪切变形的影响，而Kerr 地基模型通过多参数的加入，能够有效地提高地基模型下土与结构相互作用的响应精度。基于此，本文作者在前人研究的基础上采用两阶段法分析桩-土相互作用，第一阶段通过LOGANATHAN等[5]提出的解析公式估算隧道开挖引起周边土体自由水平位移，第二阶段将桩基简化成Timoshenko 梁[22]放置在Kerr 地基模型上，建立桩基水平向受力平衡方程，并结合桩基两端约束情况获得桩基水平向变形响应应答。随后考虑群桩之间土体遮拦效应获得隧道开挖引起邻近群桩水平向变形半解析解。将本文方法计算结果与已有的工程实测和有限元数据对比，验证了本文方法的正确性，最后进一步分析了地层损失比、隧道埋深、桩隧相对位置变化对桩基水平向变形及其内力的影响。

1 理论推导过程

1.1 隧道开挖引起周边土体自由场水平位移

LOGANATHAN等[5]就软土地区土体变形特性提出隧道开挖引起周围土体自由位移变化公式，其表达式为

式中：ε为地层损失率；R为隧道半径；y为桩基截面中心点到隧道轴线处水平距离；x为桩身某点距离地面的竖向距离；H为隧道轴线埋深深度；v为均质土体泊松比。

1.2 盾构开挖引起邻近单桩水平位移解析

为了简化计算，Kerr地基模型如图1所示，并做出以下假设：

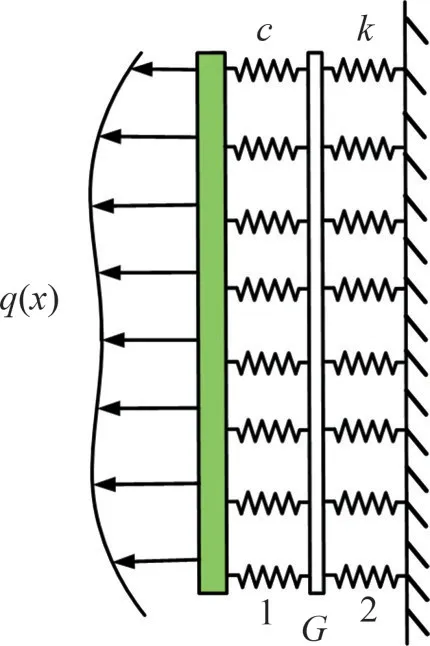
图1 Kerr地基模型Fig.1 Kerr foundation model

1)既有桩基简化成Timoshenko 梁搁置在弹性地基上；

2)桩-土相互作用满足Kerr地基模型要求；

3)桩基为常为L的弹塑性连续变形体，不考虑结构物与土体存在相对位移，土与结构变形协调一致。

1.3 桩基变形理论推导

根据Kerr 地基模型理论知，桩基变形w(x)满足式(2)：

式中：w1(x)为第1层弹簧的变形量；w2(x)为第2层弹簧的变形量。利用两层弹簧的受力特性得到式(3)和式(4)：

式中：p1(x)为第1 层弹簧反力；c为第1 层弹簧刚度。

式中：p2(x)为剪切层下方第2层弹簧反力；k为第2层弹簧刚度。

对于剪切层受力特性有：

式中：G为土体剪切层刚度。

将式(2)～(4)合并可得：

桩基受到的附加应力q(x)可表示为

式中：V(y，x)为式(1)中土体水平自由位移场。

考虑到Timoshenko梁[22]的曲率方程为

式中：M为梁所受弯矩；EI为梁体抵抗变形抗弯刚度；q(x)为梁体所受到附加应力；Δ=κGaA为梁体剪切刚度；Ga为梁体剪切模量；A为梁体横截面面积，对于圆形截面，κ一般取0.9。

根据Timoshenko梁[22]理论可知：

假设其剪切层满足

式中：Mr为梁剪切层的弯矩。

将式(5)～(8)代入式(9)，可得：

样品测试在武汉综合岩矿测试中心进行，采用的测试方法为等离子体发射光谱法、X射线荧光光谱法、原子荧光光谱法、发射光谱法、石墨炉原子吸收法、离子选择性电极法、催化极谱法、化学发射光谱法等。样品测试质量采用了标准样、密码样、监控样等多种监控手段，并通过了中国地质调查局区域地球化学分析质量监督检查组的验收，分析质量为优秀级。

式(11)为隧道引起邻近既有桩基的水平变形控制方程。本文为了简化计算方法，采用有限差分法使其获得6 阶方程数值解。将既有桩基离散为n+7 个点(其中桩基两端存在6 个虚点)，相邻虚点之间间距为l，且l=L/n，其中L为桩长。桩基离散化如图2所示。

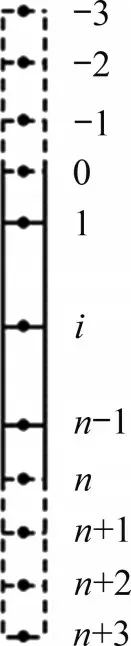
图2 既有桩基离散图Fig.2 Discretization of existing pile

那么式(11)可化为

式中：(w2)i-2，(w2)i-1，(w2)i，(w2)i+1及(w2)i+2分别代表节点i-2，i-1，i，i+1及i+2水平位移。

结合式(6)～(9)可知桩基水平位移w(x)、弯矩M(x)、剪力Q(x)的表达式为：

为了消去桩基两端6个虚拟单元，本文将桩基两端简化成两个自由端，这样可知桩基两端弯矩M=0，剪切层弯矩Mr=0，剪力Q=0，即

K1，K2，K3和K4以及Q1，Q2和Q3分别表示为：

此时，便获得w2(x)位移的半解析解，将得到的结果代入式(13)～(15)即可得到桩基水平位移w(x)、弯矩M(x)、剪力Q(x)。值得注意的是，当Timoshenko 梁剪切刚度Δ=∞时，本文解析将退化成Euler-Bernoulli梁下的Kerr地基模型解析(E-K模型)；当Kerr 地基模型中参数c=0 时，本文解析将会退化成Timoshenko 梁下Pasternak 地基模型解析(T-P模型)。

1.4 盾构开挖对邻近群桩水平位移分析

当盾构过程侧穿邻近群桩时，相邻桩基对土体应力传递的阻碍作用使得桩身处的土体自由位移减小，此现象就是群桩的遮拦效应。实际群桩水平附加位移应是隧道开挖引起的邻近土体自由水平位移与邻近桩基间遮蔽效应产生的水平位移之和。

图3所示为开挖隧道侧穿邻近群桩简化计算模型图。若只考虑单桩时，隧道开挖引起桩1轴线位置土体自由水平位移为V1(x)，而桩1 轴线处实际水平位移为S1(x)，那么桩1 处土体产生的遮蔽位移为

图3 隧道与群桩位置图Fig.3 Location diagram of tunnel and pile group

式中：ΔS1(x)为隧道侧穿引起桩1位置处产生的土体遮蔽位移。

桩1轴线处遮蔽效应引起桩2轴线位置处土体位移V21(x)为

λ为水平向土体传递系数，

式中：V2(x)为隧道开挖在单桩2轴线处产生的土体自由水平位移。

此时在隧道开挖引起群桩中桩2轴线处土体实际自由水平位移为

1.5 Kerr地基模型参数确定

根据ZHNAG 等[17]的建议，土体弹簧刚度k可参照文献[23]的建议取值，土体剪切层刚度G可由TANAHASHI[24]提出的经验公式取值，具体如下：

式中：Es为地基弹性模量：t为地基剪切层厚度：v为均质土体泊松比。本文参照以往研究[25]，近似将11D(D为桩的直径)等效为地基土的剪切层厚度。

参照简化弹性空间法[26]，Kerr的地基参数c取

2 算例分析

2.1 已有文献单桩算例对比

文献[17]报道了隧道开挖侧穿邻近单桩的工程实例，其简化图如图4所示。工程实况如下：圆形截面单桩直径D=1.2 m，单桩插入深度L=28 m，桩基模量Ep=30 GPa；隧道轴线埋深H=15 m，隧道轴线与桩基轴线水平距离y=5.7 m，隧道成后半径R=4.125 m，地层损失率ɛ=0.5%。基于文献[17]地层分层情况及其建议，取本算例中土体模量Es为54 MPa。

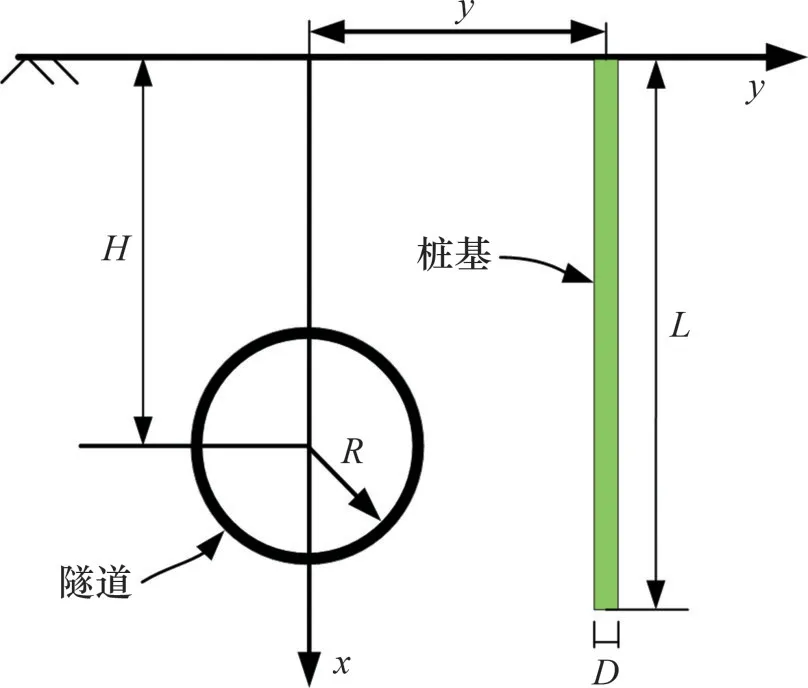
图4 隧道与桩基的位置示意图Fig.4 Location diagram of tunnel and pile foundation

图5所示为本文方法计算结果与文献[17]中计算结果对比图，其中三种方法均是采用差分法获得桩基变形解析，且三种结果变化趋势与实测结果一致。既有理论是将桩基简化成Euler-Bernoulli梁搁置在单参数Winkler和双参数Pasternak地基模型上，而Winkler地基模型并未考虑到土体剪切效应，很明显计算结果与实测结果偏差很大；Pasternak 地基模型考虑了土体剪切效应的因素，但其计算结果与实测结果也存在一定的误差；但很明显Pasternak 地基模型预测结果与实测结果更接近，从两种地基模型计算结果可以看出，土体剪切效应对于土与结构相互作用的研究是不可忽略的。相比于Pasternak 地基模型预测结果，本文方法既考虑到了多参数对提高计算精度的作用，也考虑到了Timoshenko 梁考虑到梁体剪切刚度的影响，其计算精度提高明显，更加贴近于实测结果。可见本文方法相比于现有的计算方法，具有一定的优越性。

图5 单桩水平位移分析(与已有文献对比)Fig.5 Analysis of horizontal displacement of single pile(compare with existing paper)

2.2 既有文献群桩算例比较

本算例以LOGANATHAN 等[27]三维边界元GEPAN 软件模拟隧道开挖引起邻近2×2 群桩水平位移，并与本文方法计算结果进行对比验证。隧道与群桩简化模型如图6所示，其假定均质土体弹性模量Es=24 MPa，泊松比υ=0.5，桩基模量Ep=30 GPa，桩底距离地表深度L=25 m，桩基直径D=0.8 m，隧道开挖半径R=3 m，隧道轴线埋深H=20 m，地层损失率ɛ=1%。隧道轴线与前排桩水平距离y1=4.5 m，隧道轴线与后排桩水平距离y2=6.9 m。

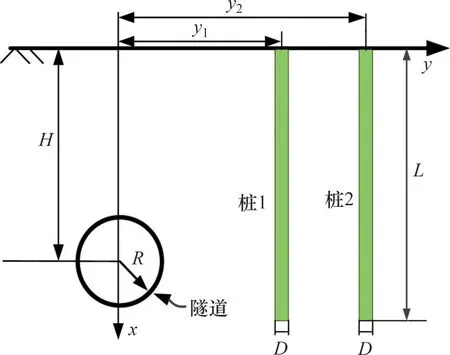
图6 隧道与群桩简化示意图Fig.6 Simplified diagram of tunnel and pile group

为了验证本文方法的有效性以及本文方法退化解与本文方法的差别，图7和图8所示分别为本文方法、T-P模型、E-K模型与有限元结果桩2水平位移和弯矩对比图。由图7和图8可以看出：三种方法计算结果与有限元结果趋势相同，而T-P模型预测结果明显偏大。本文作者认为这是由于未考虑到Kerr地基模型参数c加入，使得本文方法计算精度有了较大提高。相比于本文方法，E-K模型位移结果偏小，但其弯矩预测结果偏大，本文作者认为这是E-K模型没有考虑到梁体剪切刚度会削弱梁体抵抗外力变形的影响，这样会使得Euler-Bernoulli 梁抵抗外力变形的能力增强，但其承担的弯矩内力也会变大。从图7 和图8 可以得出：本文方法和E-K模型均能较好预测桩2水平位移及弯矩变化，从而验证了本文方法的有效性。

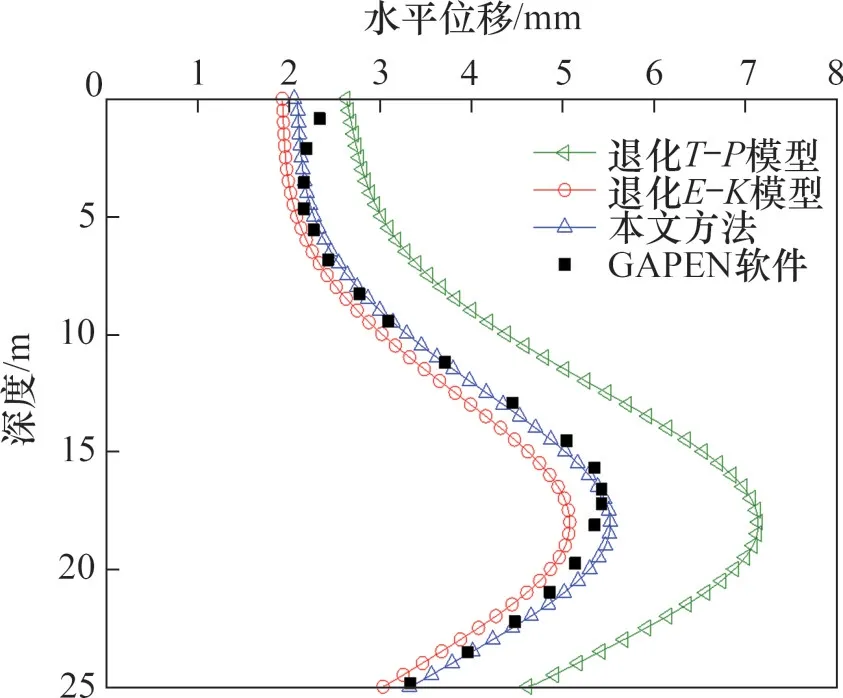
图7 桩2水平位移Fig.7 Horizontal displacement of pile 2

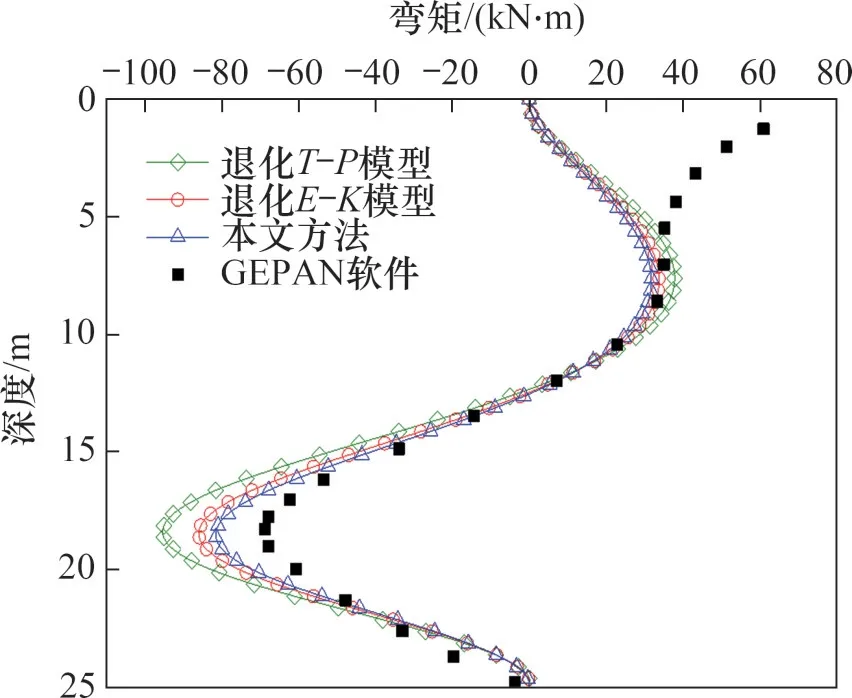
图8 桩2弯矩Fig.8 Bending moment of pile 2

3 参数分析

为了研究土体损失率、隧道埋深、桩隧位置变化对桩基受力变形影响，以LOGANATHAN等[27]三维边界元GEPAN 模拟隧道引起邻近2×2 群桩变形响应的工程为例。本文利用控制变量法对桩土相互作用进行参数分析。

3.1 地层损失率对既有群桩的影响

为研究地层损失率对隧道开挖引起邻近群桩变形响应的影响，取5 组不同地层损失率ɛ进行参数分析，ɛ分别为0.5%，1.0%，1.5%，2.0%和2.5%时采用本文方法计算桩2变形响应。

图9 和图10所示分别为基于不同地层损失率下，隧道开挖引起邻近群桩中桩2水平位移和弯矩响应图。由图9可知：桩2的水平位移峰值随着地层损失率增大而增大，地层损失率每增加0.5%，其峰值增幅基本上保持恒定。由图10 可知：在不同地层损失率下，桩2弯矩峰值变化与桩2水平位移峰值变化相似。本文作者认为这是由于桩基轴线处土体自由位移场与地层损失率变化成正比关系，增大地层损失率会同步线性增大桩基的水平附加应力，这样也会使得桩2产生实际水平位移也在等比例增大。

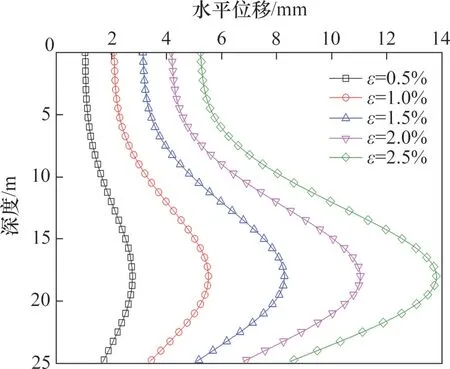
图9 不同地层损失率下的桩2水平位移Fig.9 Horizontal displacement of pile 2 with different ground loss ratios

图10 不同地层损失率下的桩2弯矩Fig.10 Bending moment of pile 2 with different ground loss ratios

3.2 隧道埋深对既有群桩的影响

为研究隧道埋深对隧道开挖引起邻近群桩变形响应的影响，取5组不同隧道埋深H进行参数分析，H分别取14，16，18，20 和22 m，并采用本文方法计算桩2变形响应。

图11 和图12所示分别为不同隧道埋深下，隧道开挖引起邻近群桩中桩2 水平位移和弯矩响应图。由图11可知：隧道埋深从14 m增至22 m的过程中，桩2 水平位移峰值缓慢增大，其增幅较小，位移峰值出现的位置深度也在不断增加。从图12可知：隧道埋深从14 m 增至22 m 的过程中，桩2弯矩峰值由3个逐渐变为2个；当隧道埋深靠近桩底时，弯矩峰值明显减小。基于此，对于实际工程中盾构侧穿既有邻近群桩时，应尽量增大开挖隧道的埋深。

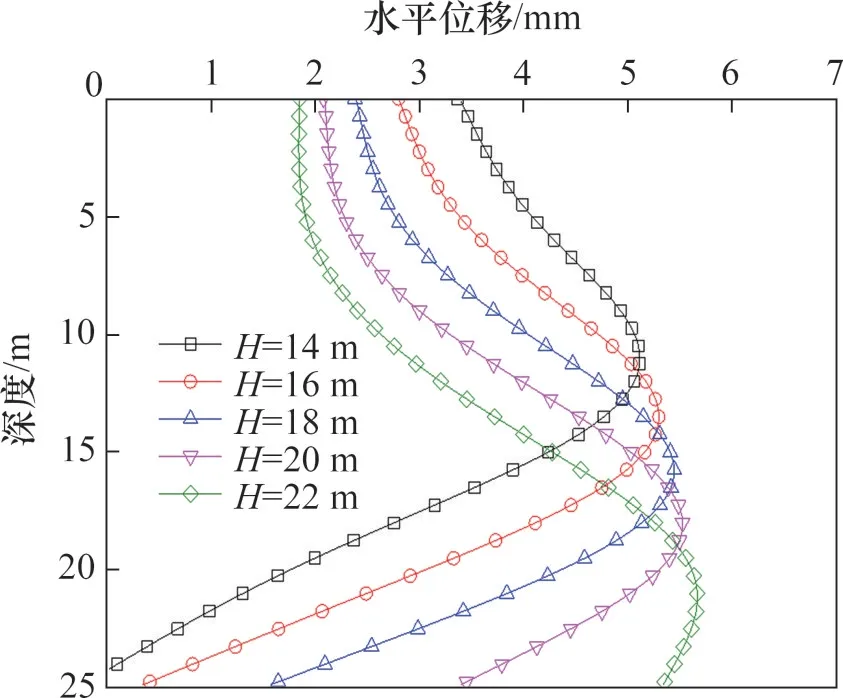
图11 不同隧道埋深下的桩2水平位移Fig.11 Horizontal displacement of pile 2 with different depth of tunnels

图12 不同隧道埋深下的桩2弯矩Fig.12 Bending moment of pile 2 with different depth of tunnels

3.3 桩隧位置对既有群桩的影响

为研究桩隧位置的改变对隧道开挖引起邻近群桩变形响应的影响，取5组不同桩隧距离y2进行分析，y2分别取7，8，9，10和11 m，并采用本文方法计算桩2变形响应。

图13 和图14所示分别为不同y2下，隧道开挖引起邻近群桩中桩2水平位移和弯矩响应图。由图13可知：y2从7 m增至11 m的过程中，桩2水平位移峰值逐渐减小，但其速率是不断变缓的。由图14可知：在不同y2下，桩2弯矩峰值的变化与桩2水平位移峰值变化相似。本文作者认为这是由于随着桩2位置越来越远离隧道开挖轴线时，隧道开挖引起桩2位置处的自由位移场也会逐渐减小，同样的桩1 对桩2 的遮蔽位移也逐渐减小，使得桩2的水平位移和弯矩不断减小且其减小速率也在变缓。

图13 不同y2下的桩2水平位移Fig.13 Horizontal displacement of pile 2 with different values of y2

图14 不同y2下的桩2弯矩Fig.14 Bending moment of pile 2 with different values of y2

4 结论

1)基于两阶段法，采用LOGANATHAN 公式获得隧道开挖引起邻近土体自由水平位移场，再将桩基简化成Timoshenko 梁搁置在Kerr 地基模型上，并结合桩基两端边界条件获得既有桩基变形解析应答。

2)通过与既有理论及其工程实测结果对比，说明了相比于传统的单参数Winkler 和双参数Pasternak 地基模型差分解结果，本文方法预测结果更加符合实测结果；与既有文献有限元结果对比，本文方法计算结果基本符合有限元结果，且相比于本文方法退化解更既有优越性。

3)邻近群桩水平位移及其弯矩会随着地层损失率增大而线性增大；隧道埋深增大会引起邻近群桩水平位移减小，且隧道埋深接近于桩底时，桩基弯矩峰值会明显减小；桩隧间距增大会引起邻近群桩水平位移及其内力减小，其减小速率逐渐变缓。