灵活解题，培养学生创新思维

颜小兵

数学的创新思维要求学生敢于质疑，敢于创新，探索不同解法之间的异同点，通过对不同之处作比较，类似之处寻根源，不断提升解题能力和思维品质。

一、原题呈现

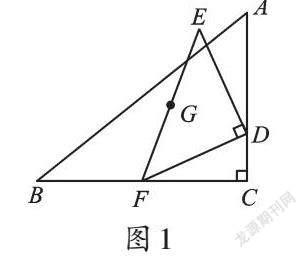
例题 如图1，在Rt△ABC中，∠C=90°，AB=10cm，BC=8cm，点F为边BC的中点，点D从点C出发沿CA向点A运动，到点A停止，以FD为直角边作等腰直角三角形DEF，点G为斜边EF的中点，求点G运动的路径长为多少？

此题为一道中考复习练习题。教师在解决这类问题时，首先要让学生弄清点G在运动过程中，其运动路径是什么形状，找出点G运动的起点和终点，才能根据相关计算求出路径的长度。在解题教学的过程中，教师应关注学生创新思维的培养。

二、教学过程

1.合作探究，把握问题

师：同学们，要想求出点G运动的路径长，你们认为点G运动的路径是什么？

生1：我认为点G在一条直线上运动。

生2：我认为点G的运动轨迹是线段。

师：为什么？请大家分组讨论。

学生分组讨论。经过一番讨论后，大部分学生得到以下猜想：点G的运动可以参照点E的运动，因为点G是线段EF的中点，点G始终随着点E的运动而运动，可以由点E的运动轨迹求出点E的路径长度，从而确定点G的路径长度。

师：大家说得都很好，思维很活跃。同学们能否联想到基本模型，去确定点E的运动轨迹呢？

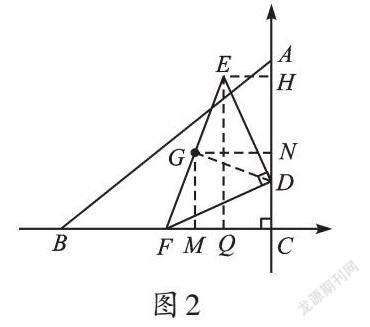
生3：我们可以建立平面直角坐标系，过点E作EH⊥y轴，垂足为H（图略），利用基本模型证明三角形全等，确定点E的运动轨迹。

师：说得非常好。你说的基本模型其实就是“K”字形模型，它是平面几何中最常见的模型之一。若能够灵活运用此模型结论，我们就可以轻松破解本题。我们要能够观察发现点G的运动路径是△EDF的中位线，探索出点G、点E的运动路径之间的数量关系，再根据三角形的中位线定理，求出点G运动的路径长。

2.品味模型，寻求多解

师：同学们，刚刚我们借助于点E的运动轨迹去求点G的路径长。那么，我们能不能直接通过探究点G的运动轨迹去求点G的路径长？

生4：可以。点G的运动轨迹应该是在一条直线上，而且是在第二、四象限的角平分线上。

师：是的，点G始终在∠ACB的角平分线上运动。这样我们就可以由点G的起点和终点直接求出点G的路径长度。我们可以构造“K”字形模型表示点E的坐标，然后根据中点公式求出点G的坐标，确定点G在函数y=-x的图像上，从而求出点G的路径。

师：既然大家都已经知道点G的轨迹在∠ACB的角平分线上，那么你能不能利用其他方法来证明呢？

生5：分别作EH、GN垂直于y轴，EQ、GM垂直于x轴。我们可以利用三角形中位线定理和梯形中位线定理求出GM和GN的长度相等（如图2），然后利用角平分线的逆定理判断确定点G始终在∠ACB的角平分线上运动，从而求出点G的路径。

3.深化问题，创造多解

师：同学们，只有一组对角是直角的四边形，我们把它称之为“损矩形”。你能不能利用“损矩形”GFCD的特征，证明点G到∠ACB的两边的距离相等？

生6：连接GD，分别过点G作AB、AC的垂线段。

（学生板书略。）

师：很好，通过直接探讨点G的运动轨迹，运用“损矩形”的特征，证明了点G到∠ACB的两边的距离相等，再根据角平分线逆定理，从而确定点G始终在∠ACB的角平分线上运动。同学们，还有其他证明方法吗？

（学生沉默片刻，教师继续引导。）

师：根据刚才提出的“损矩形”的特征，我们连接它的两个非直角顶点的线段，这条线段叫作损矩形的直径，你们发现点G、F、C、D之间有什么关系？

生7：四点共圆。

师：为什么？

生7：我们分别连接GC、GD，取公共斜边FD的中点O，连接GO、FO、CO、DO，可以证得GO=FO=CO=DO，所以它们四点共圆。

师：说得非常好！怎样说明点G在∠ACB的角平分线上呢？

生8：连接GC、GD，根据同弧所对的圆周角相等得到，∠GCF=∠GDF=45°。因为∠ACB是直角，从而直接确定点G始终在∠ACB的角平分线上运动。

师：那我们怎样去求线段的长度呢？

众：因为点G的运动轨迹是一条线段，我们直接利用两点间的距离公式就可以求出点G運动的路径长。最后求出点G运动的路径长为3[2]。

三、教学反思

习题讲评课不能仅停留在对错题的分析、讲解上，而应更加关注学生思维能力的发展，以题目为支点，撬动学生良好思维品质的发展。在本题中，笔者从辨别图形结构、挖掘基本图形入手，不断追问，拓展问题，让学生认清问题本质。特别是在中考前夕的复习课中，教师应精心选择例题，结合多方面的知识点，从多角度探索典型例题的不同解法。同时，教师还要给足学生思考的时间，适时引导并留白，启发学生思考，让学生发挥想象力，创造性地产生许多新的解题方法，引导学生深入探究反思，发展数学学科素养，培养创新思维。

（作者单位：江苏省泰州市姜堰区实验初级中学）