基于GAF与卷积神经网络的配电网故障选线新方法

雷 静，李晨婧，郭 亮，王晓卫，徐经民，黄灿英

（1.国网江西省电力有限公司电力科学研究院，南昌 330006；2.国网江西省电力有限公司，南昌330006；3.西安理工大学电气工程学院，西安710054；4.江西建设职业技术学院，南昌 330200）

中国配电网大部分采用中性点经消弧线圈接地系统，即小电流接地系统[1]。根据统计，小电流接地系统发生单相接地故障的概率高达80%，而在消弧线圈的补偿下，故障特征弱，给配电网故障选线增加了一定困难。如果继续允许故障长时间运行，系统绝缘易受损害，造成故障范围扩大为两相短路。因此必须准确判断故障线路并及时切除，以免造成更严重的危害。

配电网故障选线方法众多，包括相关分析法[2-3]、电压法[4]、导纳法[5-6]、注入信号法[7]和智能算法等。由于故障特征和选线结果呈现复杂的非线性关系，不能用一个准确的数学模型来描述，而智能算法无需人为设定线性关系，自动从数据中学习来调整参数，所以近些年来，智能算法被广泛应用于配电网接地故障选线。文献[8]将各馈线零序电流和相电流差进行小波变换，计算综合相关系数之后输入SVM进行学习分类，得到故障选线结果；文献[9]将HHT处理后的特征矩阵奇异值分解提取幅值和极性特征量，通过模糊C聚类算法判定故障；文献[10]通过LCD、希尔伯特变换以及带通滤波算法获取时频矩阵，经过奇异值分解后利用SVM分类器选线；文献[11]利用改进欧式-动态弯曲距离法提取特征矩阵，再利用模糊C均值聚类实现选线。

深度学习作为智能算法一个新的研究方向，在语音和图像处理方面颇有建树，近年来，卷积神经网络逐渐应用于电力系统故障判别，文献[12]利用卷积神经网络进行配电网故障区内区外定位，验证了卷积神经网络用于配网故障判别的可行性；文献[13]利用连续小波变换后的零序电流时频分量，转化为灰度图，输入卷积神经网络进行故障选线；文献[14]将原始一维零序电流波形拼接为新的特征图像，这种方法可以扩充样本库，提高神经网络训练的精度；文献[15]对传统GoogLeNet网络的结构进行改进，能更好地提取图像的特征进而提高网络分类正确率；文献[16]将零序电流进行S变换后，构造S变换相关度图形SCF（S-transform correlation figure），再利用卷积神经网络提取SCF特征进行配电网故障选线。

本文将一维零序电流序列利用GAF变换转化为二维特征图像，再输入卷积神经网络，提出一种基于格拉米角场和卷积神经网络的配电网故障选线方法，并对该方法利用单一样本库和含3种完全不同拓扑样本的混合库都进行验证，证明了该方法的正确性和干扰适应能力。

1 单相接地故障特征分析

据现有文献可知，谐振接地系统发生单相接地故障后，半周波到一周波内故障接地电流会有暂态过程，此过程蕴含丰富的暂态信息，利用暂态过程的电气量进行分析，可以使故障特征的提取更有效。接地电流if表达式为

式中：第一项为稳态分量，后两项为暂态分量；iCt和iLt分别为暂态电流的电容Ct分量和电感Lt分量；ICm和ILm分别为电容Cm电流和电感Lm电流的初始值；ωf和δ分别为电流电容分量的振荡角频率和衰减系数；τL为电感电流的衰减时间常数；ω为工频角频率；φ为故障初相角。

由于电感电流补偿的滞后性，接地电容在零序电压作用下的充放电过程会产生显著的暂态过程，使故障馈线和健全馈线的零序电流波形有明显不同的暂态特征。

为进一步分析发生单相接地故障后的物理特征，给出图1简化后接地故障零序等效网络，当发生单相接地故障时，流过健全馈线与故障馈线的电流具体如图所示，以其为例分析谐振接地配电网系统发生单相接地故障时的零序电流特征。图中，母线有n条出线，线路l发生单相接地故障，u0为母线零序电压。

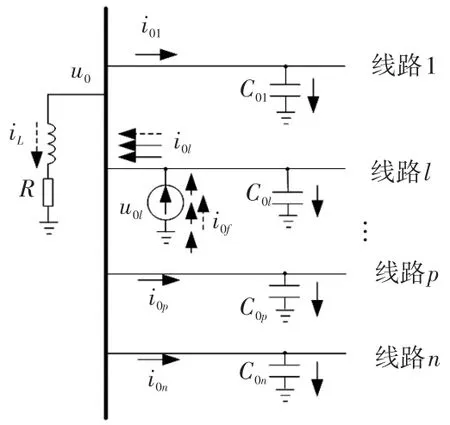
图1 单相接地时故障零序等效网络Fig.1 Zero-sequence equivalent network under singlephase grounding fault

从图1可以看出，非故障线路p零序电流电压关系为

对于故障线路l，故障线路零序电流为

由式（2）可知，健全馈线由于处在相同的零序电压之下，它们的零序电流表达式相同且波形拥有很强的相似性。另外，由式（3）可以看出，故障馈线的零序电流大小等于所有健全馈线零序电流与消弧线圈电流之和，其幅值远大于健全馈线；其次，两者之间的极性也近似相反。

线路1故障各馈线零序电流如图2所示。如图2（a）所示，当线路l1发生单相接地故障时，l1的零序电流幅值几乎等于其他健全馈线零序电流幅值相加，并且l1的零序电流相位近似相反于其他健全馈线相位，这印证了上述故障馈线和健全馈线的特征。但是随着故障工况的变换，如图2（b）所示，故障馈线和健全馈线的相位不再严格相反，而且幅值规律也有所变化，所以需要提出一种可以适应多种故障工况的选线方法。

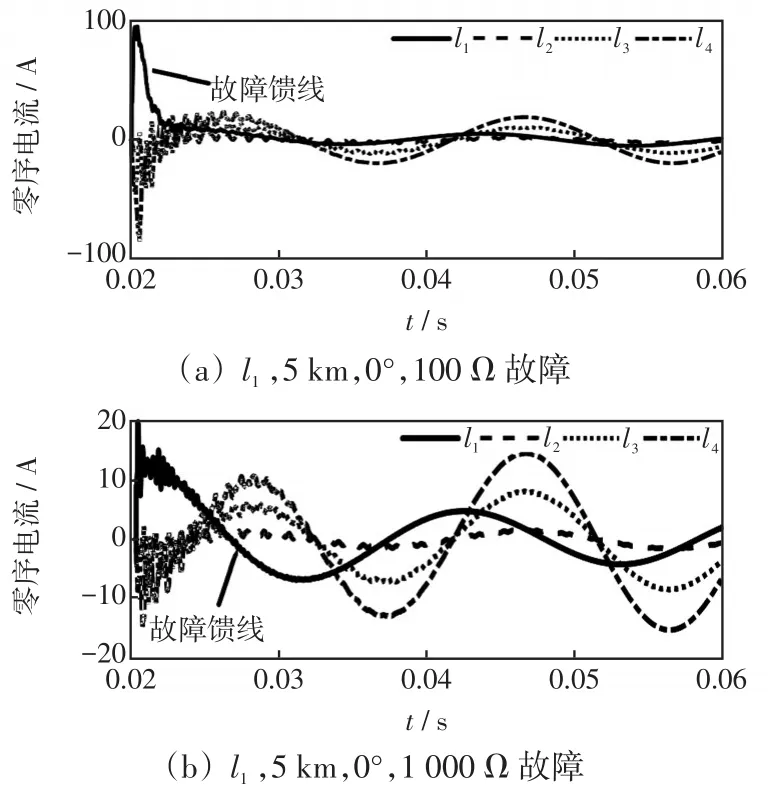
图2 线路1故障各馈线零序电流Fig.2 Zero-sequence current of feeders under fault in line 1

2 故障选线方法

本文提出了一种基于格拉米角场和卷积神经网络的谐振系统配电网单相接地故障检测方法。将采集到的零序电流信号数据进行GAF变换，将生成的包含故障馈线和健全馈线特征差异的特征图GASF（Gramianangularsummationfield）/GADF（Gramian angular difference field）输入到多层CNN网络中。经过训练集代入卷积神经网络训练，得到训练好的CNN，再代入测试集，以此区分待测馈线是否故障。

2.1 GAF变换

GAF变换技术，可以将一维序列的数据表示为极坐标，再利用极坐标生成二维图像[17]。在将一维序列X={x1，x2，…，xn}映射到极坐标之前，将数据归一化至[0，1]，即

式中：xmin为序列中的最小值；xmax为序列中的最大值；x͂i为一维序列归一化后的值。再将一维序列映射到极坐标，即

式中：ϕi为极坐标角度，取值在之间；ri为半径。将区间[0，1]分割成n块间距相等的部分，半径ri是前i块的累加。如此，随着时间序列的推移，相应数据都能在极坐标系上找到对应的点。

如图3（a）所示，所有零序电流序列值的极坐标角度都在0和π/2之间，半径大小与时间先后对应，其中故障线路l1的角度分布与其余健全馈线有明显不同。这样做有两个好处：一是给定一个时间序列，在极坐标系上的映射有且只有一个结果；二是极坐标系通过半径大小保留了时间先后关系。

之后，形成一个类gram矩阵，即

收集每条馈线单相接地故障发生后一段波形数据，然后通过上述GAF变化将一维数据转化为二维特征方阵，如图3（b）所示，之后就可以将这些特征图作为CNN的输入样本集。

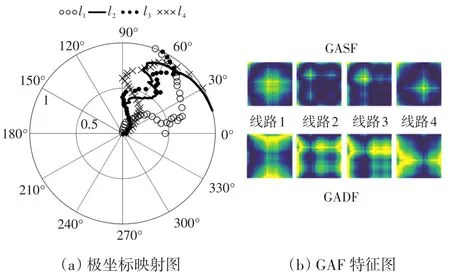
图3 极坐标下线路1故障各馈线零序电流Fig.3 Zero-sequence current of feeders under fault in line 1 under polar coordinates

CNN会分别对GASF图和GADF图进行训练，后面测试结果表明，CNN对GADF图的分类比GASF图的分类更准确。

2.2 基于卷积神经网络的故障馈线检测

卷积神经网络对格点元素，例如像素和音频的特征提取、学习有稳定的效果。在第2.1节，将配电网馈线的电流序列信息通过GAF变换转化为二维格点元素，之后就可以利用CNN进行线路故障判别。

本节介绍了一个多层卷积神经网络，网络各层架构如图4所示，总体结构包括8层结构，除去输入层和输出层，隐含层中还包含了6个隐层，分别是2个卷积层、2个池化层、1个全连接层和1个分类层。最后一个池化层的输出被送入全连接层，通过Softmax函数，数据被分为2类。

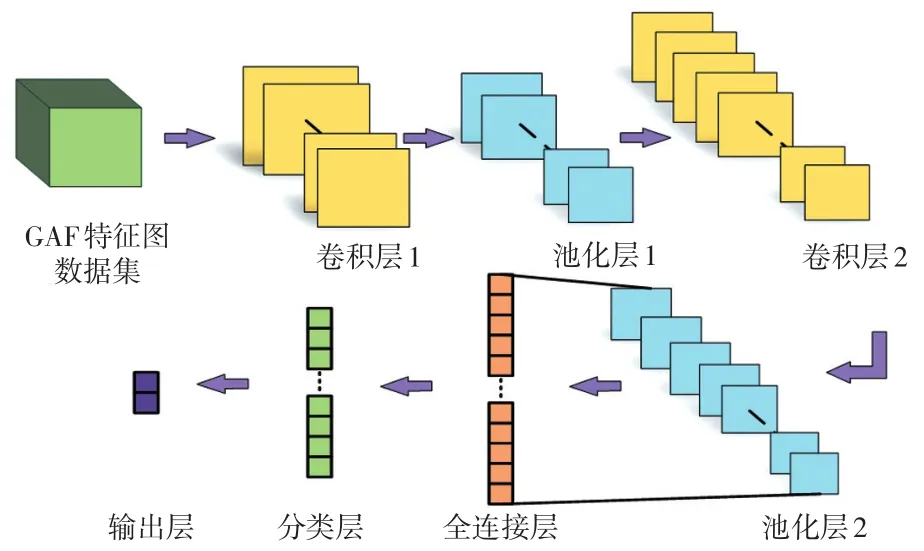
图4 CNN网络架构Fig.4 CNN network architecture

2.2.1 卷积层

卷积层的计算公式为

式中：j为神经网络的层数；X为输入图像子区域集合；z为第z个输出的图像；为第j层的输出；为第j层的输入；为卷积核；为偏置；f（·）为激活函数，一般为Relu函数。

2.2.2 池化层

池化层使用特征图像中某一位置相邻输出的总体统计特征来代替网络在该位置的输出，采用最大值池化函数或者平均值池化函数进行特征映射，从而降低特征图维度与训练计算量，但不改变特征图数目。

池化层的计算公式为

式中：yk为第k个输出图像；ymn为输出大小m×n的特征图；wk为权连接系数（权值）；bk为偏置；down（·）为池化函数。

2.2.3 全连接层

在人工神经网络中全连接表示每一层中的神经元均与前一层中的神经元建立权连接关系。取全连接层的输入图像的个数为i，尺寸为m×n。先把i个输入的图像矩阵按列展开，然后按照上一层的输出顺序首尾相接，拼接成一个i×m×n的一维特征列向量，最后将其映射至输出层相应的类别。全连接层与输出层的映射表达式为

式中：yg为输出层的第g个值；x为特征向量；wg为权连接系数（权值）；bg为偏置；f（·）为激活函数，一般为Softmax函数。

2.2.4 输出层

全连接层的输出，经过Softmax函数被分为两类，分别为馈线健全和故障的概率，表示为

式中：P0为馈线判定为健全馈线的概率；P1为馈线判定为故障馈线的概率。选取概率大的类别为馈线判定结果。

2.2.5 丢弃层

在卷积神经网络中使用丢弃层，可以防止网络过拟合，增强其泛化能力。该层将上一层输出数据按一定比例丢弃，其实是让某些神经元以一定的概率不工作，采用dropout后计算公式变为

式中：rj为Bernoulli函数以概率p随机生成一个0、1的向量；zj为该层输出。可以理解为在每次训练网络时，使用dropout，每个神经元有p的概率被移除，这样可以使一个神经元的训练不依赖于另外一个神经元，协同作用被减弱，从而减少过拟合情况的发生。

2.2.6 损失函数

神经网络中，为了克服使用均方误差训练时，权重和偏置更新非常慢的缺点，常使用交叉熵代价函数作为损失函数loss，用以迭代训练更新参数，即

式中：x为样本；n为样本总数；a为网络输出；y为输出真实值。

利用loss函数可以评判神经网络迭代训练的效果，选取合适的网络结构和参数，以便利用所构建的卷积神经网络进行馈线故障判定。

通过本节构建CNN架构，之后利用事先采集的零序电流序列对CNN进行迭代训练，获得CNN参数。采集母线零序电压u0以及各馈线零序电流i0的波形。将母线零序电压u0大于额定相电压的15%作为选线流程的启动条件。满足启动判据时，收集的待测零序电流i0序列将进行GAF特征变换，之后输入预先训练好的CNN中，实现故障馈线判别，流程如图5所示。

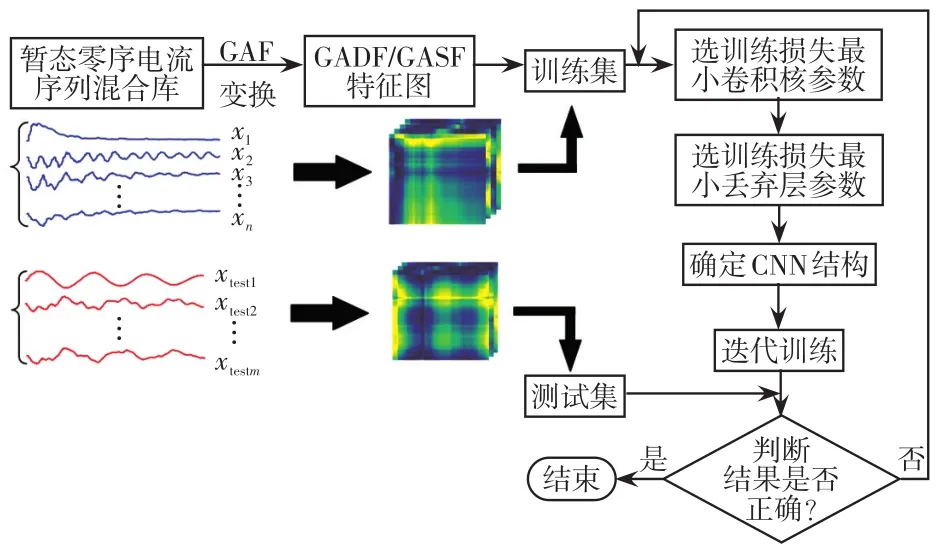
图5 接地故障选线方法Fig.5 Grounding fault feeder selection method

3 仿真验证

3.1 混合库模型

为了验证本文所提方法的通用性，对不同拓扑、参数、馈线类型和故障条件的配电网模型进行仿真，通过设置不同的接地故障工况，产生大量数据。单相接地故障是在不同故障条件下设置的，包括不同的故障馈线、每条馈线不同故障位置，不同接地电阻及不同故障初始角等。

3.1.1 辐射状网络模型

在仿真软件中搭建了一个典型的10 kV辐射状配电网模型，该故障仿真模型采用10 kV的4条馈线配电系统，如图6所示。架空线路和电缆线路参数如表1所示，辐射状网络模型的接地故障工况参数如表2所示。

图6 辐射状配电网模型Fig.6 Model of radial distribution network

表1 模型参数Tab.1 Model parameters

表2 故障工况参数Tab.2 Parameters under fault conditions

3.1.2 IEEE-13节点模型

采用仿真软件搭建了一个IEEE-13节点模型，如图7所示。

图7 IEEE-13节点配电网模型Fig.7 Model of IEEE-13-node distribution network

对该模型进行不同故障工况的单相接地仿真，其中节点645和646是BC两相，节点684是AC两相，所以将其他三相线路划分为3块区域，分别记为l1、l2和l3，并在这3块区域安装零序电流互感器，用来记录零序电流。

在线路l1上共设置4处单相接地故障点，分别距线路首端60.96 m、91.44 m、121.92 m、152.40 m，接地电阻从0 Ω到2 000 Ω，4条线路总共仿真132条波形。

3.1.3 IEEE-34节点模型

采用仿真软件搭建了一个IEEE-34节点模型，如图8所示，该算例是位于亚利桑那州的实际线路。

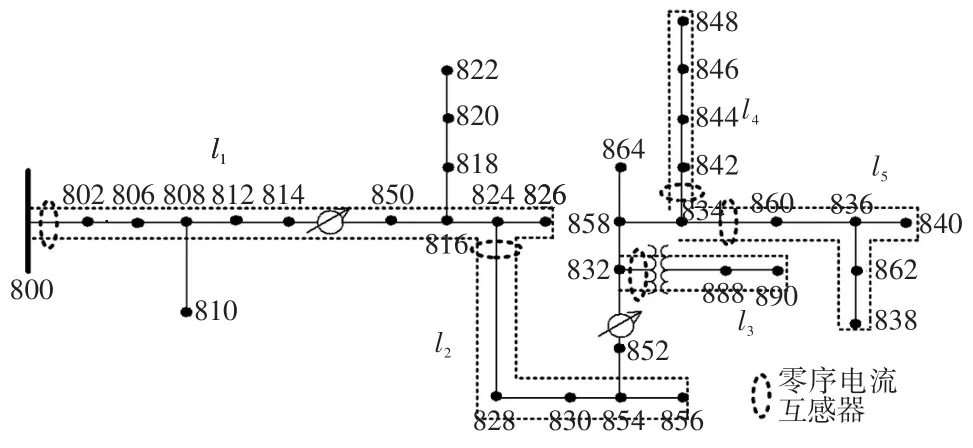
图8 IEEE-34节点配电网模型Fig.8 Model of IEEE-34-node distribution network

对该模型进行不同故障工况的单相接地仿真，除去单相线路，将模型三相线路划分为5块，并在线路上安装零序电流互感器，用来记录零序电流。

在线路l1上共设置4处单相接地故障点，分别距线路首端60.960 m、131.826 m、527.304 m、9 823.704 m，接地电阻从0 Ω到2 000 Ω，5条线路总共仿真220条波形。

3.2 混合数据库建立

3.2.1 采样方法

对上述模型采样时，选取辐射状网络的一维原始零序电流波形，采样频率为100 kHz，信号的采样点数为100。但对于IEEE-13节点和IEEE-34节点网络，未发生故障时系统本身就是不平衡状态，因此对零序电流突变量进行采样效果更好，即发生故障后的零序电流减去上一个周期正常运行状态的零序电流，表示为

式中：N为每周期采样点数；xk+N为当前时刻零序电流采样值；xk为上个周期正常运行状态的零序电流采样值。采集3种模型的零序电流突变量作为初始数据，通过第2.1节所述变换，转化为可以输入CNN的特征图像。

图9是采集的辐射状网络（l1为故障线，l2、l3、l4为健全线）、IEEE-13节点模型（l1为故障线，l2、l3为健全线）和IEEE-34节点模型（l1为故障线，l2、l3、l4、l5为健全线）的零序电流突变量GAF变换的特征图。3种模型均为线路1发生单相接地故障的情况，对它们的零序电流突变量进行GAF变换，得到GADF/GASF特征图，其中故障线路1与其他健全线路的特征图有明显区别，CNN经过训练后可以很好地区分健全馈线和故障馈线的特征。

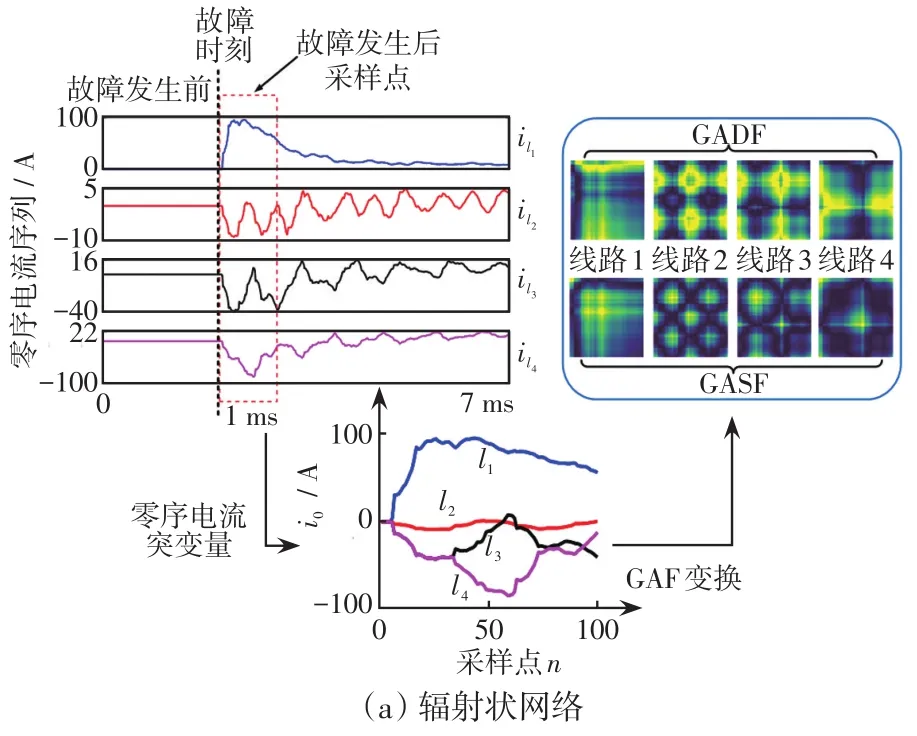
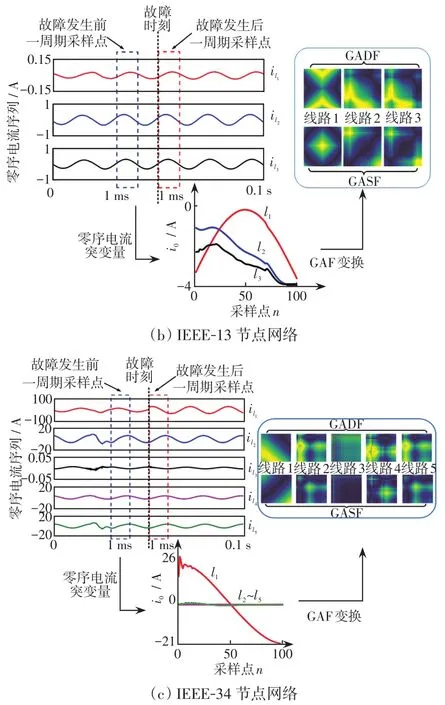
图9 配电网模型GAF变换Fig.9 GAF transformation for distribution network model

3.2.2 数据库划分

在本例中，对馈线的检测分类采用2个类别标签，分别为故障馈线和健全馈线。建立3种模型进行仿真，采样零序电流突变量数据，构建如下2个样本库。

（1）辐射状模型样本库：共2 288个样本，打乱样本，从中随机选择2 058个作为训练样本，剩余的230个作为测试样本。

（2）混合样本库（包含辐射状网络模型和IEEE-13、IEEE-34节点模型）：共528个样本，其中IEEE-13节点仿真波形132条，IEEE-34节点仿真波形220条，为了平衡3种模型样本数量，从辐射状模型样本库选取176条仿真波形。打乱样本，从中随机选择472个作为训练样本，剩余的56个作为测试样本。

3.3 网络参数确定及训练

本文仿真试验在个人计算机（Windows 10，内存8 GB）上完成。CNN采用Python 3.8和Tensor-Flow 2.2.0深度学习框架搭建。基于所提出的CNN结构，将模型仿真波形进行GAF变换，每个样本为100×100的二维矩阵图像，将它们分为训练和测试样本，用于检验所提方法的正确率。

3.3.1 核大小的选取

使用不同的卷积核和池化核大小，会对卷积神经网络的性能造成影响。分别设置不同的卷积核和池化核大小，对神经网络训练后再进行对比，比如“3-2-3-2”表示卷积层1的核大小为3×3，池化层1的核大小为2×2，卷积层2核大小为3×3，池化层2核大小为2×2。

如图10所示，将卷积神经网络迭代训练100次的损失值进行比较，可以看出“7-2-3-2”结构收敛速度最快而且迭代100次后损失值最低，所以最终确定卷积神经网络的参数为“7-2-3-2”。

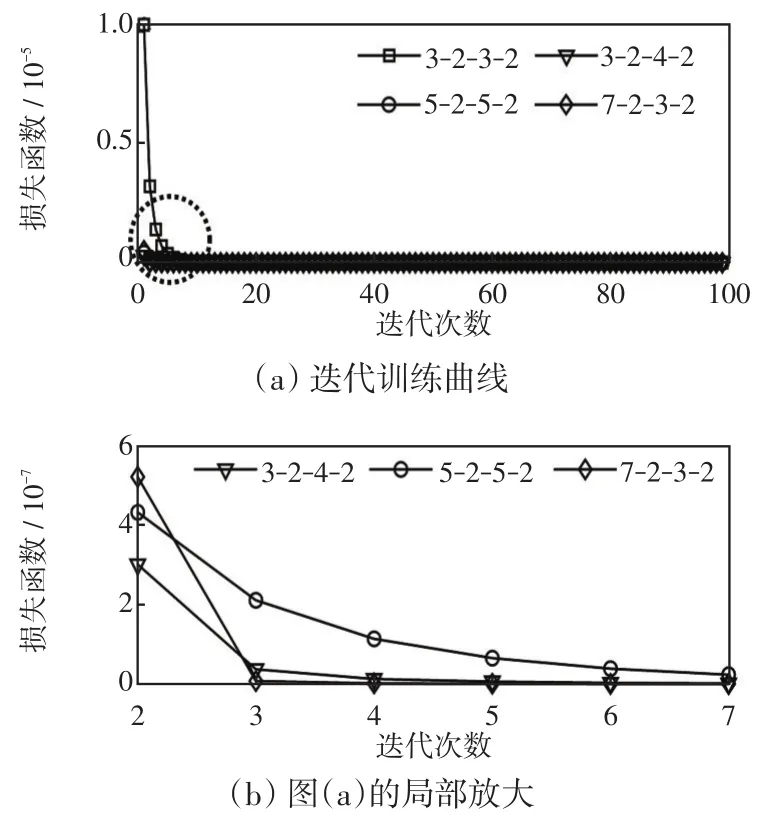
图10 CNN迭代训练曲线（1）Fig.10 Iterative training curves of CNN（1）

3.3.2 丢弃层参数的确定

设置不同的丢弃概率训练CNN，对第3.2.5节中丢弃层的参数进行选择。CNN迭代训练曲线如图11所示。

由图11可以看出，随着迭代次数的增加，损失逐渐降低，而p=0.3相较其他概率，CNN训练的损失更低。所以选择丢弃层参数p=0.3。

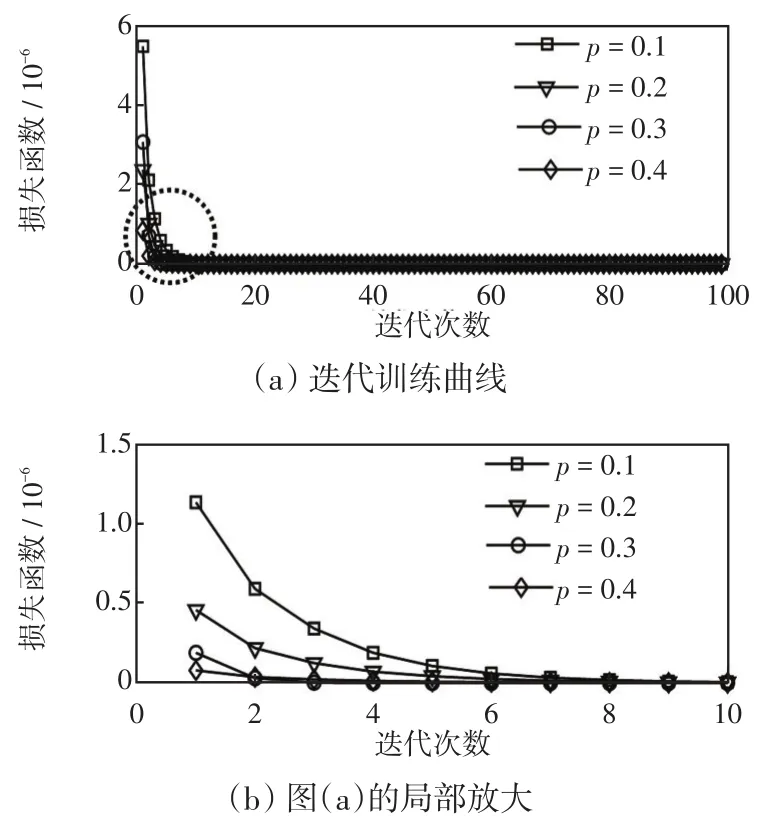
图11 CNN迭代训练曲线（2）Fig.11 Iterative training curves of CNN（2）

由于确定了CNN一些核大小以及丢弃层的参数，所以以CNN基础结构为基础，提出CNN各层结构如表3所示，利用该CNN模型对图像进行特征提取和故障馈线识别。

表3 CNN各层结构Tab.3 Layer structure of CNN

3.4 网络提取故障特征分析

为分析CNN提取故障特征的过程，本文选取230个样本。利用第3.3节介绍的CNN网络进行迭代训练，将最后几个隐含层的输出可视化，如图12所示。

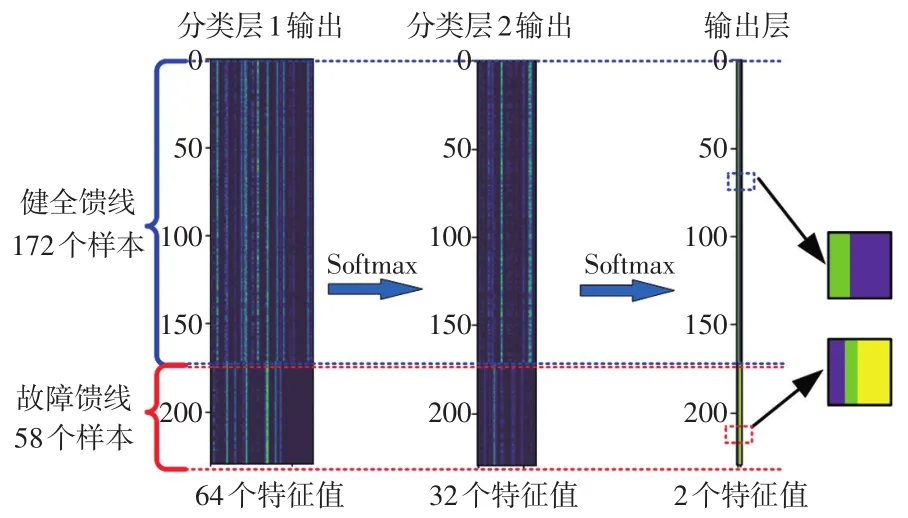
图12 CNN隐含层输出可视化Fig.12 Hidden layers output visualization of CNN

由图12可以看出，CNN最后几层数据经过Softmax函数的传递，样本特征的维数逐渐被降低，在保留样本图片特征的基础上，随着层层传递，样本的特征区别更加鲜明，说明所提出的CNN有较好的区分健全馈线与故障馈线的能力。

当CNN迭代训练次数在0、100时，将其分类层1的输出结果提出，采用t-SNE进行降维并归一化，可视化到xy二维平面上，结果如图13所示。

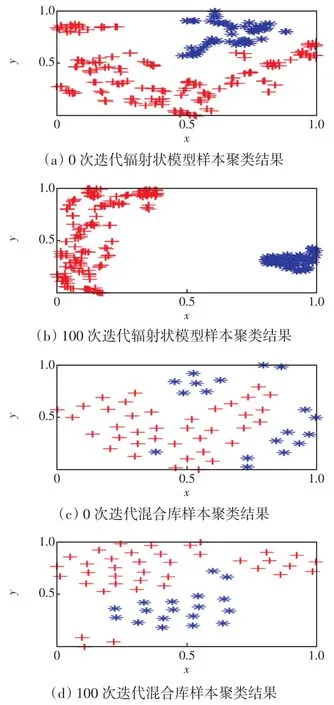
图13 t-SNE聚类结果Fig.13 Clustering result of t-SNE

从图13可以看出，辐射状模型由于样本标签少，分类能力非常高；对于混合库来说，虽然样本来源工况复杂，但仍具有良好的分类效果，说明CNN具有良好的自动提取故障特征的能力。随着迭代次数的增加，故障类型逐渐分开，同类型的馈线标签更紧凑，同时也进一步展现了CNN模型优越的识别性能。

3.5 模型验证结果

将CNN多层模型训练迭代后，代入测试集进行验证。图14中的混淆矩阵显示了对馈线正常或故障所执行的分类任务结果。在这些分类任务中，输入图像为从零序电流信号产生经GAF变换后的GASF和GADF特征图。

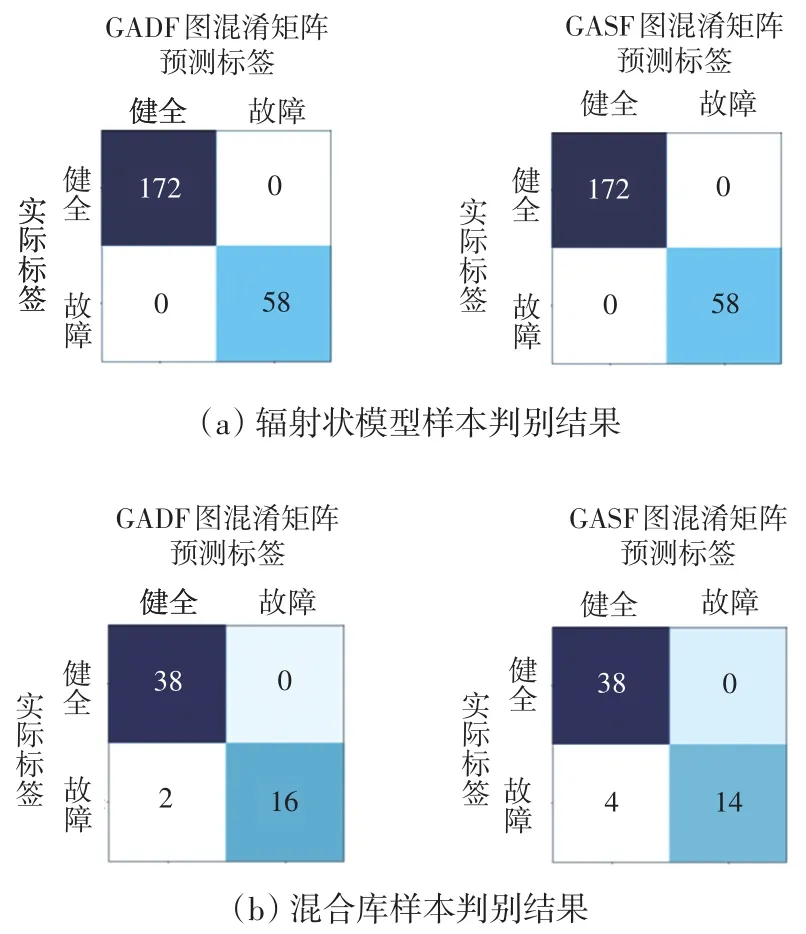
图14 故障判别混淆矩阵Fig.14 Confusion matrix of fault diagnosis

从图14可以看到，混淆矩阵显示了对等待判别馈线（测试集）所执行的分类任务结果。例如图14（b）中的GADF图混淆矩阵展示了56个测试样本的实际标签和预测标签，其中38个健全样本被正确地预测为健全标签，16个故障样本被正确地预测为故障标签，但是有2个实际故障样本被误判为健全样本。对于辐射状模型测试馈线，如图14（a）所示，在GAF+CNN的方法下，全部判别正确。对于混合库样本，如图14（b）所示，有个别故障馈线被判断为健全馈线，但是准确率依然很高。而且随着迭代次数的增加，分类的准确率也在逐步上升。

支持向量机SVM（suppout vector machine）是一种常用的归纳学习智能算法，SVM通过寻找最优超平面将两类对象分隔开。对于配网故障选线，SVM将其转化为二分类问题，输入为一条零序电流序列，输出将馈线分为故障和健全两类。SVM、GASF+CNN及GASF+CNN的判别测试准确率结果如表4所示。

表4 测试结果Tab.4 Test result

表4中的预测输出结果表明对馈线标签所执行的分类准确率，在不含干扰的工况下，对于辐射状模型样本库来说，GASF+CNN和GADF+CNN的判定准确率达到100%，均高于SVM方法。对于混合样本库来说，GADF+CNN方法的选线准确率最高有96.43%，GASF+CNN和GADF+CNN方法选线准确率依然均高于SVM方法。

需要说明的是，混合库由于涉及模型数量多，仿真样本数量少，选线准确率没有辐射状样本库高，但是在不含干扰的工况下，本文方法对其选线准确率依然高达96.43%，随着样本数量的提升，相信其准确率会有所提高。

3.6 适应性分析

在实际工程应用中，因为互感器非单一通道，信息传输可能出现超前和滞后的现象，常常出现多通道采样传回不同步现象。为了模拟这种情况，设置健全线路零序电流采样传回时间超前或滞后故障线路10%。图15为非同步传回采样的零序电流波形特征图，由于采样点为100点，所以设置故障线路零序电流采样超前或滞后健全线路10点。

由图15可见，故障线暂态零序电流序列采样滞后于健全线，滞后的n个数据补0，所以矩阵中前n行与前n列覆盖的特征值均为0计算而来。那么原本属于k行和k列的特征值，也被延后到了k+n行和k+n列。

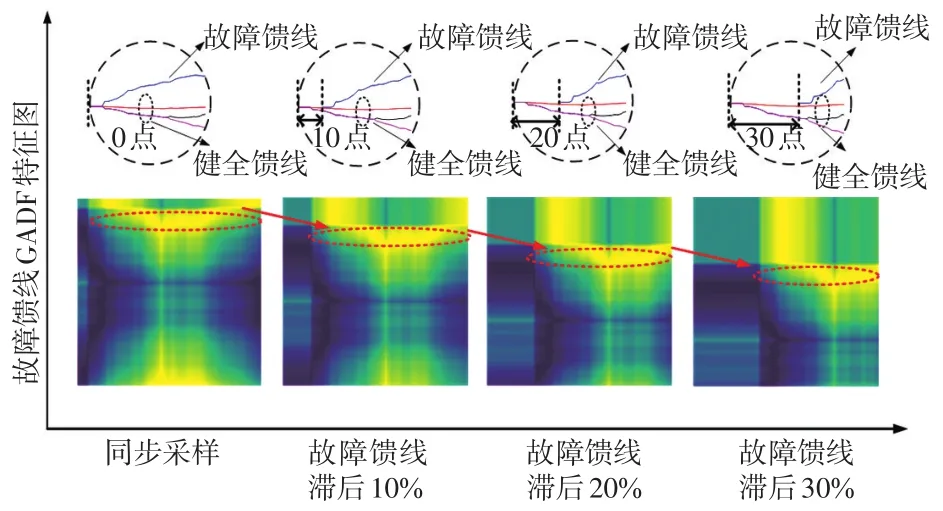
图15 非同步传回采样暂态零序电流特征图Fig.15 Characteristic images of transient zero-sequence current with asynchronous sampling

由表5可以看出，GADF+CNN方法的预测准确率在两个样本库都保持最高；对于辐射状模型样本库，本文方法表现效果良好，GADF+CNN选线准确率能达到100%；对于混合库，SVM方法表现依然不如本文方法，虽然由于混合库模型复杂，仿真样本少，但GADF+CNN方法准确率能达到90%以上，仿真样本增多可能会使混合库的选线准确率有很大的提升。结果表明，本文方法适用于非同步传回采样数据的馈线是否故障的判别。

表5 信号非同步采样测试结果Tab.5 Test results under asynchronous sampling of signal

4 结论

本文通过GAF变换将一维零序电流序列转化为二维特征图像，并构建CNN，提取GASF和GADF特征图的信息，实现馈线故障与否的判别。利用仿真数据进行验证，可以得出以下结论。

（1）利用GAF对原始零序电流波形进行变换，可以得到具有丰富特征信息的图像。将生成的GADF和GASF图像输入CNN进行训练和验证后，可以发现GADF图像的识别效果优于GASF图像。

（2）建立不同拓扑模型的混合数据库会略微降低精度，但会大大提高故障检测方法的通用性。此外，笔者还采集了大量不同故障条件下的接地故障特征图像，如不同的故障位置、不同的接地电阻、不同的故障初始角，使得该方法具有很强的多工况适应性。

（3）与SVM方法相比，本文方法尤其是GADF+CNN方法对配电网馈线判定的准确率更高，对数据非同步传回的干扰具有良好的鲁棒性，在配电网故障选线方面表现良好。