基于主从博弈的楼宇微网优化运行

王 辉，王宝全，李旭阳，王一凡，金子蓉

（1.三峡大学电气与新能源学院，宜昌 443002；2.湖北省微电网工程技术研究中心（三峡大学），宜昌 443002）

随着我国“双碳”目标的确立，可再生能源RGs（renewable generations）在电网中的全面有机整合是未来电力系统面临的主要挑战之一，以RGs为基础的分布式发电DG（distributed generation）越来越常见[1]。楼宇能耗、工业能耗和交通能耗在我国并称为三大能耗，对楼宇能耗，通过优化管理可以节约20%～30%能耗[2]，节能潜力巨大。随着DG、能量储能系统、用户负荷以及电动汽车和智能模块（智能电表、开关）在中低压系统中利用，形成微电网。微电网不仅用于调峰、负载转移和能源管理，还最大化RGs集成，减少与主电网的交换功率[3]。楼宇微网BMG（building microgrid）为提高建筑能耗效率提供了机会和理想的基础设施，是智能电网的重要组成部分。

有关微电网优化调度国内外均有一定的研究[4-10]，现阶段主要研究供需双侧协同优化。文献[5]提出一种分层调度策略实现微电网的经济可靠运行，避免可控发电机组频繁启动，提高可再生能源利用率；文献[6]建立了微网两阶段优化调度模型，提出一种动态激励型需求响应参与的实时滚动优化策略，结果表明所提策略可提高用户收益，降低系统运行成本；文献[7]考虑供给侧、需求侧及能源转换之间影响作用，构建了供需双侧多能协同优化策略模型，通过实际算例验证了所提模型在夏季和冬季均具有显著经济和环境效益；文献[8]提出了一种基于需求响应的多能源型微网多时间尺度调度方法来优化协调能源供应侧、能源需求侧和储能设备；文献[9]利用供需双侧电、热能的互动互补关系，建立多能互补的微网优化运行数学模型，通过算例分析，验证文中建立的模型可以提高系统供能的灵活性；文献[10]在以热电联供CHP（combined heat and power）机组为核心的微网上建立了考虑需求侧热、电协同响应的规划模型，以经济性指标和环境性指标为多目标函数，仿真结果表明所提模型能降低碳排放和提高系统经济性。上述研究对微电网参与市场交易提供重要理论基础，但微电网在产能、耗能环节包含多方利益主体，各利益主体之间优化相互制约，考虑单方主体利益优化，势必影响其他主体利益，在优化过程中需要同时考虑各主体利益。

博弈论是一种先进的优化工具，主要用于研究多个利益相关主体如何进行优化决策的问题[11]，已经应用在电力系统的优化运行和能量管理等领域。在BMG优化调度中，楼宇微网运营商BMO（building microgrid operator）调度与用户用能调度的目标具有不同逐利特性，博弈论可以有效解决此问题[12-13]。文献[14-15]使用Stackelberg博弈对运营商和用户之间的电力交易过程建模，通过优化日前电价来最大化运营商的利益，然后用优化电价来诱导用户调整用能，减少用户的用电费用。用户用能包括多种能源形式，上述文献从单一电力方面进行调度，不能发挥用户的多能可调度潜力。文献[16]提出了一种基于源荷双侧的主从博弈优化策略，以供应商、服务商及用户不同主体的经济性最优为目标，通过算例表明，所提方法可有效提高系统中各主体的经济收益，但是所构建供热设备仅有CHP机组和燃气锅炉GB（gas boiler），能源转换设备单一；文献[17]基于综合需求响应和博弈方法，提出了一种两阶段优化调度策略，经过算例验证所提调度策略优越性，实现了不同主体间制约平衡和联合优化，但是CHP机组固定的“以热定电”模式运行和能源转换设备单一；文献[18]考虑系统运行经济性和环保性建立了合作博弈模型，对各能源耦合设备利益分配，结果表明提出的利益分配方法有效可行，但是系统采用固定的“以热定电”模式；文献[19]以“以热定电”策略为基础，提出了运营商与产消费者的博弈模型，以实际算例验证了无论在双方经济效益上还是负荷特性都有优势；文献[20]提出基于主从博弈的分布式协同优化运行策略，通过混合算法求解，验证了供能侧收益和用能侧消费者剩余都提升。上述文献中，CHP机组大多工作在传统的“以热定电”模式，运行在传统固定模式下，系统整体收益降低，目前在基于博弈优化中对运营商模式选择研究不足。

文献[21]考虑“以热定电”模式的不足，分析“以电定热”模式的优势，在供需博弈优化模型中对比两种不同模式，验证了“以电定热”模式能提高供需两侧的收益，但也造成了大量热能浪费。用户侧的热电比不是固定的，运营商在固定模式下收益都不是最优的。文献[22]提出一种运营商动态选择模式，但未考虑到可再生能源对运营商模式选择的影响。现有研究中，对供能侧能源转换设备研究单一，不能充分利用能源之间耦合提高系统经济收益。

针对以往研究不足，结合楼宇微网应用实际情况，在供能侧除了风光可再生能源发电、CHP机组外，设置对GB和电热设备的选择，增加能源之间耦合，提高系统经济收益。考虑可再生能源对运营商模式选择的影响，提出一种灵活切换模式。在优化过程中，BMO根据用户负荷需求优先制定价格策略，用户侧再根据价格信息做出需求响应，二者之间博弈过程存在先后顺序，因此将BMO作为领导者，用户聚合商作为跟随者，建立主从博弈模型，并证明该博弈模型存在唯一的Stackelberg均衡解，提出自适应差分进化SADE（self-adaptive differential evolution）算法对比运营商在不同模式下优化，并验证本文所提方法和策略的优越性。

1 BMG结构

BMG结构如图1所示，包括BMO和用户聚合商不同主体。

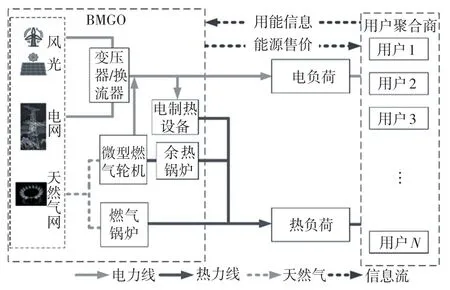
图1 超环面电机结构Fig.1 Structure of toroidal motor

BMO既是产能基地也是调度中心，包括DG、能源转换设备和能量管理系统，具有监听所辖范围内的天气参数和楼宇用能需求，与上级电网进行购、售电交易等功能。在维持系统稳定运行的同时，通过调整自身运行策略和制定售能价格来提高收益。

楼宇用户的用户管理系统既可以接收电价、热价信息，又以价格型IDR参与系统优化调度中，分散的楼宇用户参与系统优化会增加调度负担，因此用户聚合商聚合各用户的用能信息，同时也是为了避免各用户单独与运营商交互，导致用户用能的数据泄露。

BMG优化主要是供需两侧的经济联合优化，运营商根据用户聚合商提供的用能信息，调整自身的设备运行策略并制定电、热能售价，而用户聚合商接收制定的售价，发布给每个用户，由用户管理系统调整用能策略。

2 楼宇微网系统模型

2.1 楼宇微网运营商模型

2.1.1 定价模型

为了保证微网稳定，微网与电网并网运行，与电网交易的购、售电价分别表示为

BMO与用户交易的电价和热价为

式中：λep与λhp分别为BMO与用户交易的电价向量和热价向量；分别为t时段的电价和热价。

为保证BMO制定价格合理有效，防止BMO“价格套利”和用户直接向电网购电，定价约束为

2.1.2 优化模型

BMO通过向用户供能产生收益，当产生电能过多或不足时，都需要与电网交易；产生热量过多时需要承担弃热惩罚。收益最大化为优化目标，表示为

式中：FMGO为BMO的收益；分别为t时段向用户售电和售热的收益；为与电网交互收益；为微型燃气轮机MT（micro turbine）运行成本；为GB的运行成本；为BMO产热过剩，产生能源浪费惩罚；分别为BMO向用户的供电量和供热量；，其中分别为t时段MT、WT、PV发电量和电热设备的耗电量；λgas为购气单价；L为天然气低热值；ηMT，e为MT的发电效率；、μGB分别为GB的产热量和性能系数；λab为MG产生过多热的惩罚系数；为微网的产热量。

2.1.3 供能模型的选择

为了提高可再生能源利用效率，风、光发电优先利用。CHP机组以MT为核心，产生电能同时也可以产生热能供用户使用，产热量为

在“以热定电”模式下，CHP机组根据用户热能需求产生热能，同时产生的电能结合可再生能源发电和电网保证微网中电功率平衡，应满足

在“以电定热”模式下，CHP机组根据用户电能需求产生电能，产生的热能结合GB和电热设备保证微网中热功率平衡，应满足

能源转换设备GB和电热设备选择满足

在灵活切换模式，切换模式满足

式中，FMGO，FTL和FMGO，FEL分别为CHP机组工作在“以热定电”和“以电定热”模式下BMO的收益。

2.2 楼宇微网用户侧模型

2.2.1 用户负荷模型

微网中有N户综合能源用户，用户负荷包括电负荷和热负荷。本文考虑用户的IDR行为，即电需求响应和热需求响应[23]。电负荷包括固定电负荷（如电灯、电脑、电视等）和可转移电负荷（如洗衣机、洗碗机、电动汽车等），分别表示为

式中：Li，fe和Li，se分别为用户i的固定电负荷向量和可转移电负荷向量；分别为用户i第t时段的总电负荷、固定电负荷和可转移电负荷。用户根据微网下发的电价信息自主调整可转移电负荷的功率和时间，需要满足的约束为

楼宇用户中的热负荷包括热水负荷和空间热负荷，根据人体对热舒适度有一定的模糊性，降低一定的供热量，使室内温度能维持在可接受的温度范围内。减少热需求，用户的热舒适度会降低，但是用户用能成本也降低，在一定范围内，用户自愿调节热需求。原始热负荷向量和削减热负荷向量分别表示为

式中：Li，oh和Li，ch分别为用户i的原始热负荷向量和削减热负荷向量；分别为用户i在t时段参与热需求响应后的热负荷、原始热负荷以及削减的热负荷；为可削减热负荷上限。

2.2.2 收益模型

用户聚合商在接受BMO给出的价格信号后，优化用户的电、热负荷。目标函数是最大消费者剩余[20]，用户i第t时段的优化目标为

3 楼宇微网主从博弈模型与求解

3.1 博弈模型结构

对于BMG中，用户的用能策略根据BMO制定的能源价格进行优化，优化的结果反过来会影响BMO的定价，且具有先后顺序，符合主从递阶的动态博弈情况，因此BMO作为领导者，各用户作为跟随者，主从博弈G表示为

式中，N为参与者，包括BMO和各个用户，N={BMO，users}。领导者BMO的策略为24 h售出电价、热价；跟随者的策略为各时刻可平移电负荷和可削减热负荷的功率；各参与者的收益为式（7）和式（19）定义的目标函数。

在Stackelberg博弈过程中，BMO优先制定售能价格，用户根据内部的价格优化用能策略，然后BMO根据用户用能情况优化供能策略。当BMO接受所有用户的用能信息时而不再改变售能价格时，博弈达到纳什均衡。

3.2 博弈均衡存在性和唯一性证明

当满足以下3个定理时，存在唯一的Stackelberg均衡解[25]。

定理1：博弈互动参与者的策略集是非空紧凸集。

定理2：对于领导者给出策略集后，跟随者最优策略存在且唯一。

定理3：对于跟随者给出策略集后，参与者最优策略存在且唯一。

证明：领导者的策略集满足式（3）、（4），用户侧的策略集满足式（15）～（17），所以每个参与者的策略集都是非空紧凸的，满足定理1条件。对于定理2条件，求用户收益目标函数关于和求一阶偏导得到，即

由于用电效用函数系数和用户损失热舒适度系数都是正的，二阶导数都为负，所以存在极大值点。令一阶偏导（式（23））等于0，可得到极大值点为

可见，Hessian矩阵为负定的，存在极大值点。综上所述，本文的主从博弈存在唯一的Stackelberg均衡解。

3.3 求解方法

在博弈过程中，为了防止参与者信息泄露，参与者之间信息互不透明，各参与者单独优化，因此采用分布式优化方法。

差分进化DE（differential evolution）算法是一种随机的启发式搜索算法，有较强的鲁棒性和全局寻优能力，但是传统DE易出现“早熟”现象和辨识精度需要优化，本文提出一种SADE算法，在原有固定变异算子、交叉算子的基础上，引入自适应变异算子和随机范围的交叉算子，增加搜索到全局最优解的概率和保持群体多样性。自适应的变异算子和随机范围内的交叉算表示为

式中：G和Gm分别为当前进化代数和最大进化代数；F0和F分别为传统固定的变异算子和改进后变异算子，在算法开始时，自适应变异算子为2F0，在初期保持个体多样性，避免“早熟”，随着算法进展，变异算子逐步减小，到后期接近F0；R0和R分别为传统的固定交叉算子和改进后的交叉算子，改进后的交叉算子平均值保持在R0，有助于在搜索过程中保持群体多样性。用户侧的优化目标是二次函数，参考文献[20]，采用二次规划的方法优化用户侧。在博弈求解过程中将二次规划嵌入到SADE算法中，求解流程如图2所示。

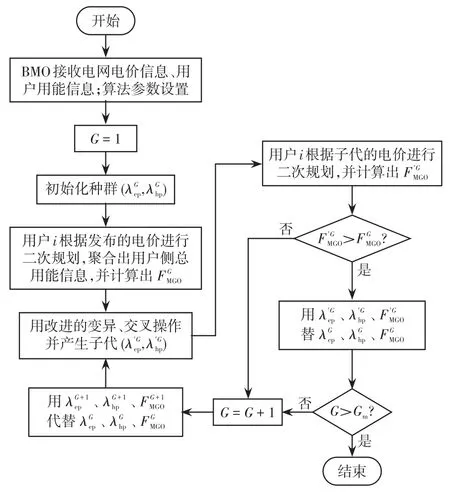
图2 求解流程Fig.2 Flow chart of solving process

4 算例分析

以北方某地的6户居民组成BMG为算例，对所提出的模型仿真，以冬季的用能情况进行分析。设备参数如表1所示，冬季典型日的风电、光伏预测出力及初始电负荷曲线和用户热初始负荷曲线分别如图3和图4所示。各用户最大可转移电负荷和可削减热负荷占总负荷的20%[20]。

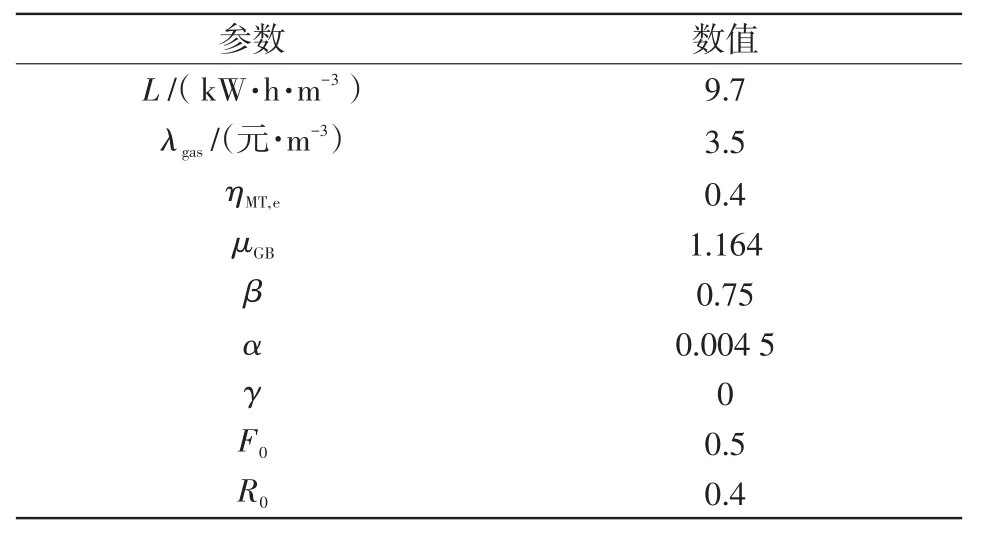
表1 设备参数Tab.1 Equipment parameters

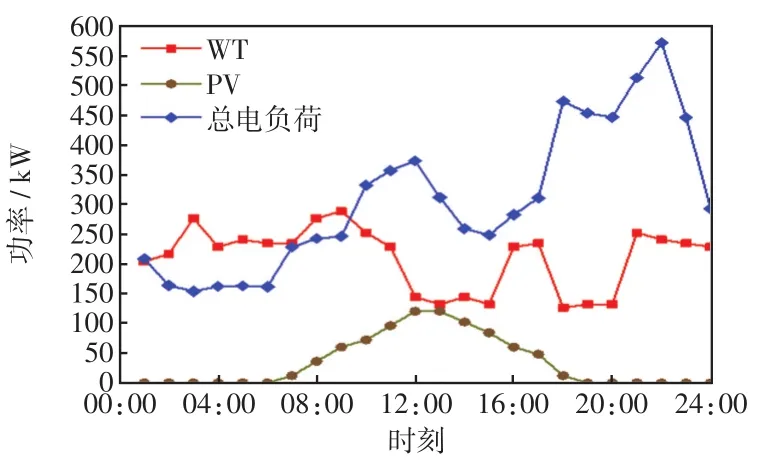
图3 风、光发电及初始电负荷Fig.3 Wind and photovoltaic power generation data and initial power load

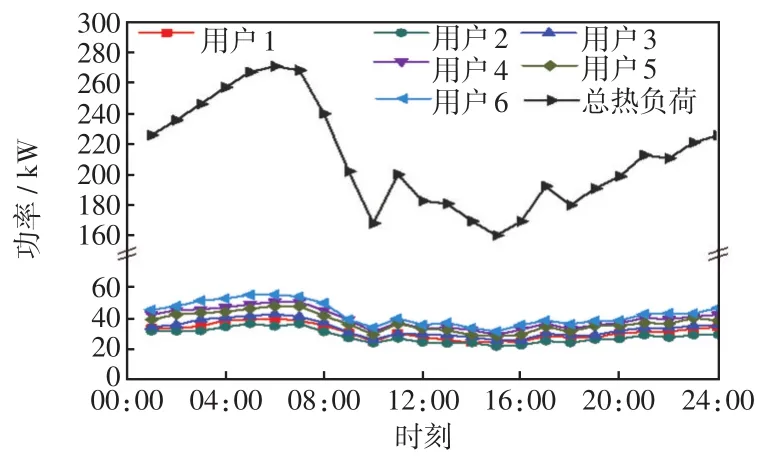
图4 用户的初始热负荷Fig.4 Initial thermal load

用户参与综合需求响应旨在降低运行成本，以往研究表明用户参与响应比不参与响应的运行成本低，因此本文只对微网运营商不同运营模式和不同算法优化设置不同场景。

场景1：BMO以传统的“以热定电”模式运行，运营商侧采用改进算法优化。

场景2：BMO以文献[21]提出的“以电定热”模式运行，运营商侧采用改进算法优化。

场景3：BMO以本文提出的灵活切换模式运行，运营商侧采用改进算法优化。

场景4：BMO以本文提出的灵活切换模式运行，运营商侧采用传统DE算法优化。

场景5：BMO以本文提出的灵活切换模式运行，运营商侧采用遗传算法优化。

不同场景下的BMO收益、用户侧成本及用户侧收益如表2所示。结果表明：“以电定热”模式比“以热定电”模式的供需两侧收益分别提高了20%和2.2%，用户侧用能成本降低；灵活切换模式比“以热定电”模式与“以电定热”模式在BMO收益上提高了23.4%和2.8%，用户侧用能成本不同程度降低。通过不同模式博弈，考虑了不同主体之间利益关系，达到各主体利益最大化。

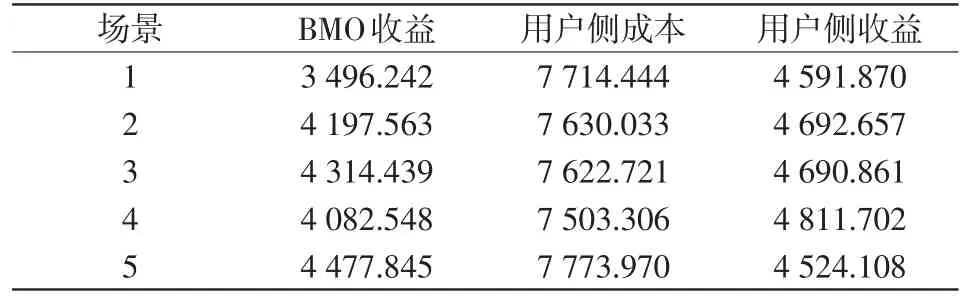
表2 不同场景下的经济对比Tab.2 Economic comparison in different scenarios 元

在“以热定电”模式下，系统运行结果如图5所示。CHP机组按照用户侧的热能需求运行，由上文经济对比分析可知，此模式下供需两侧的收益最低，主要因为当电负荷较小时，造成了电能盈余，BMO侧与电网交易时由于“价格套利”降低了收益；当电负荷较大时，BMO需要向电网侧购入电能，由制定电价机制使收益降低。对比优化前、后的电负荷表现出削峰填谷，高峰时段削减电负荷转移到低谷时段。优化后的电负荷接近新能源发电量，有助于提高新能源消纳率。

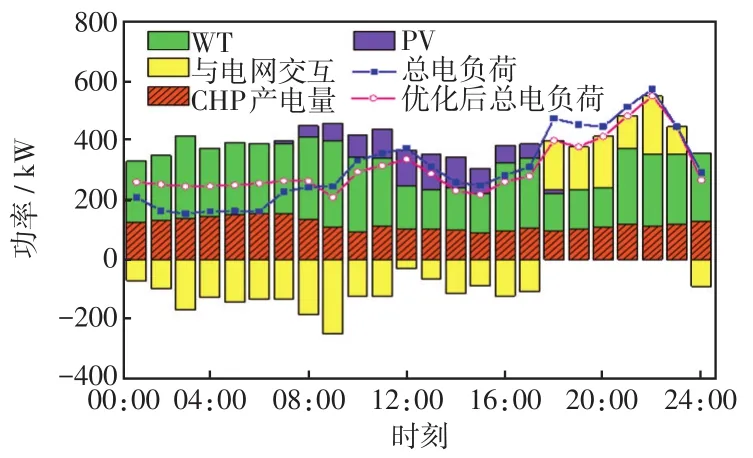
图5 “以热定电”模式Fig.5 Mode of“power following thermal load”

在“以电定热”模式下，CHP机组根据用户侧的电能需求运行，当产生热能不足时，GB与电热设备选择产生热能，满足系统热平衡，运行结果如图6所示。可见，在01：00—07：00电价低谷时段，电热费用比GB费用低，电热设备运行；其余时段热能不足时GB运行；在18：00—23：00期间，由于电能需求大，导致产生的热能多，满足用户热能后，出现了大量的弃热量，由于BMO承担弃热惩罚，使BMO收益降低。

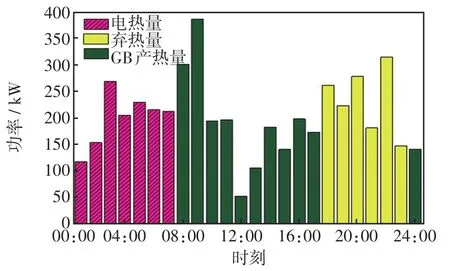
图6 “以电定热”模式Fig.6 Mode of“heat following electric load”

在灵活切换模式下，CHP机组在“以热定电”、“以电定热”和不工作3种模式下切换运行，运行结果分别如图7和图8所示。由图可见，在01：00—07：00、18：00—19：00时段及23：00时刻，CHP工作在“以热定电”模式，此期间热能需求较大，CHP机组满足优化后用户热能需求，同时产生的电能和新能源发电与电网交互满足优化后的电功率平衡；在08：00—11：00、14：00—17：00时段，CHP机组不运行状态，新能源发电与电网交互满足系统电功率平衡，此时段电价较高，电热费用高于GB产热费用，GB满足用户的热能需求；在12：00—13：00、20：00—22：00时段及24：00时刻，CHP机组工作“以电定热”模式，CHP机组产电和新能源发电满足优化后的电负荷，当同时产生热能与GB产热满足系统热平衡，因为此时段电价较高，电热费用高于GB的费用，在20：00—22：00时段，电负荷需求大，此时间段“以电定热”模式产生了多余的热量，但是整个调度周期中灵活切换模式的弃热量比固定的“以电定热”模式产生弃热量少。

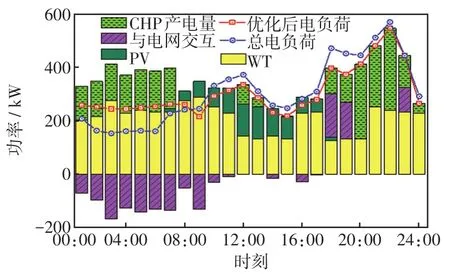
图7 灵活切换模式下电能调度结果Fig.7 Power scheduling results in flexible switching mode

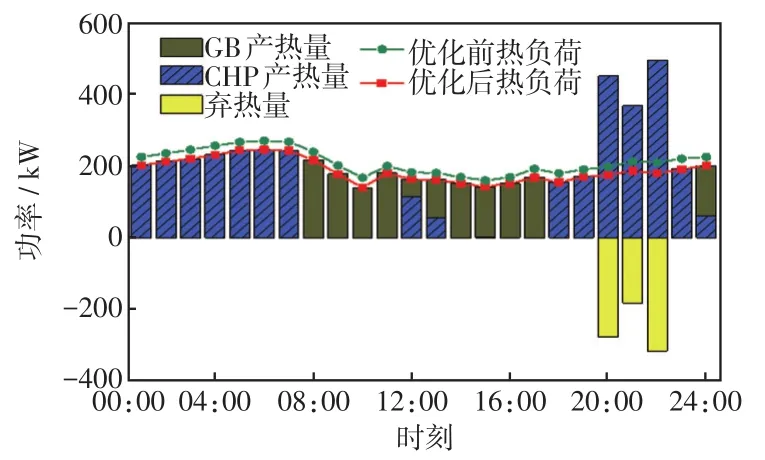
图8 灵活切换模式下热能调度结果Fig.8 Heat scheduling results in flexible switching mode

在灵活切换模式下，BMO制定的售电价、售热价如图9所示。上网电价和分时电价都是由当地电网提供的，系统制定的电价策略与电网分时电价趋势一样，比电网发布具有更优的价格。各用户热需求削减占比如图10所示，用户优化前的热需求，用户满意度最大，升高热需求和降低热需求都会降低用户满意度，用户降低热需求，用能成本减少，因此用户在一定范围内接受降低热舒适度，造成的热舒适度降低成本由用户自身承担。用户削减的热负荷量与热价变化规律相同，热价高时削减比例大。优化结果中，所有用户降低热负荷占比都在可接受范围内。

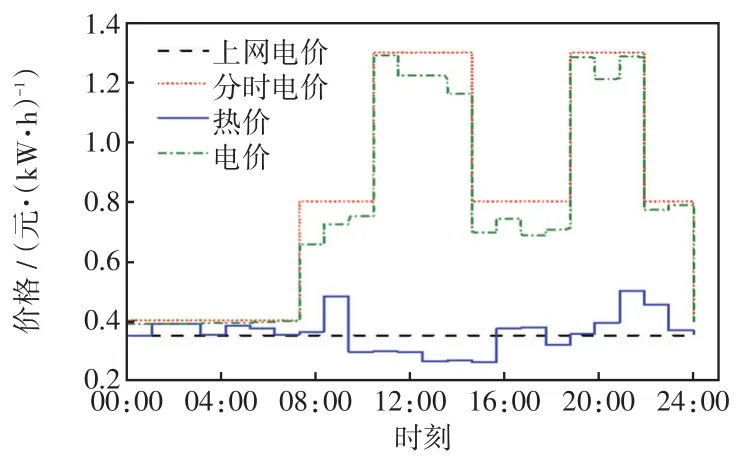
图9 灵活切换模式下BMO制定售价Fig.9 BMO pricing in flexible switching mode

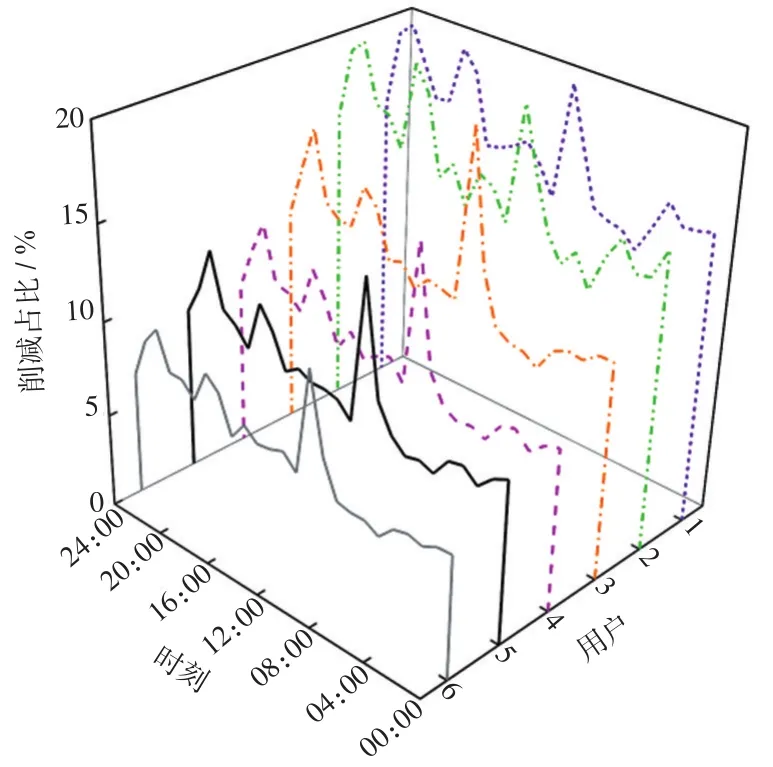
图10 灵活切换模式下热负荷削减占比Fig.10 Proportion of thermal load reduction in flexible switching mode

由于DE算法是一种随机搜索的智能算法，优化过程中具有随机性，因此在优化过程中反复优化5次。对比场景3、4优化BMO收益递代曲线如图11（a）、（b）所示，场景3、4、5优化BMO收益递代曲线5次的平均值如图11（c）所示。结果表明：本文提出的SADE算法比传统DE算法可以让种群更快速地走出死区，避免早熟，提高了BMO的收益；采用改进前后的DE算法优化BMO，在迭代60次时达到平衡，采用遗传算法优化BMO，迭代100次时达到收敛，本文使用DE算法具有较快的收敛性。

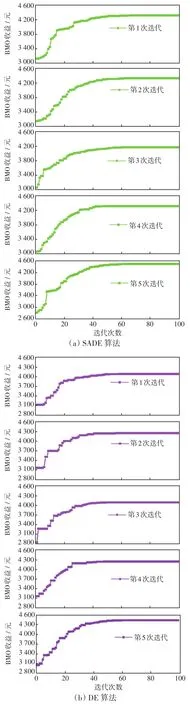
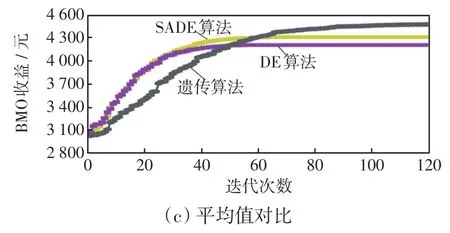
图11 BMO收敛曲线Fig.11 BMO convergence curve

5 结论

本文基于主从博弈下，为了提高楼宇微网中各主体收益，对比分析不同模式下楼宇微网优化运行，验证了博弈模型收敛性，通过算例验证了所提方法和策略的有效性，得出如下结论。

（1）所提供需双方博弈互动模型，兼顾各方的利益，不同运行模式下，都使供需两侧利益达到最大化，双方互利共赢。

（2）采用分布式优化方法递代求解，保护各主体间数据的隐私，能够快速迭代出纳什均衡解，采用提出的改进算法比传统算法更具有优势。

（3）本文设置了多种供能模型的选择，增加了能源之间耦合，用户参与IDR更灵活，有效地提高系统经济效益。

（4）提出的灵活切换模式优化可以在“以热定电”、“以电定热”和不运行3种模式下灵活选择，结果表明灵活切换模式比传统固定模式可以提高系统中各主体收益，减少用户用能成本。

本文研究CHP机组不同模式下运行状况，但是随着用户侧电动汽车增多，电动汽车充放电具有巨大的可调节性，而且电动汽车充放电不确定性和新能源发电不确定性在以后研究中需要考虑进去。