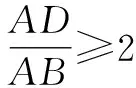抓住数学本质 考查核心知识
——一道中考压轴题的命制历程
湖北省宜昌市夷陵区东湖初级中学 黄 新 湖北省宜昌市教育科学研究院 张 钦
笔者曾有幸参加中考数学命题工作,现将中考数学试卷第23题的命题考查靶向、命题预设、素材选取、雏形编制、试题打磨等命制过程进行展示,与大家分享.
1 设想与来源
1.1 命题设想
中考是在完成义务教育基础上进行的选拔性考试,命题要考虑初中学生升入高中后继续学习的潜在能力.根据中考功能,命题组确定第23题为几何压轴题,命题定位于通过几何图形的运动与变换,借助数学活动,考查数学核心知识.命题设想以教材中的素材为原型,最好在“数学活动”中选取;重视推理,突出考查合情推理与演绎推理的有机结合[1];关注探究,注重对数学基本活动经验的考查;关注交汇,考查初中几何核心知识,规避试题模式化;注重公平,规避资料上出现的题目;强化核心,有效导向初中几何的教与学.
1.2 试题取材
查看人教版教材,笔者首先找到人教版八年级下册第64页“数学活动”中的活动1: 折纸做60°,30°,15°的角.

图1
教材原题: 如果我们身旁没有量角器或三角尺,又需要作60°,30°,15°等大小的角,可以采用下面的方法(如图1).
(1)对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平.
(2)再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM.同时,得到了线段BN.
观察所得的∠ABM,∠MBN和∠NBC,这三个角有什么关系?你能证明吗?
教材意图:教材给出利用矩形纸片折出30°角的方法,运用折的过程得到全等三角形,以及利用直角边和斜边的关系判断30°角的方法,这个活动既有动手操作,又有一定的趣味性.本活动关注学生通过动手操作和观察经历数学思考,主动获取数学知识,并感悟数学思想方法,积累基本学习活动经验,同时复习矩形的性质、三角形全等以及直角三角形等核心知识.
2 试题编制与打磨
作为中考数学试题中的几何压轴题,考查高度必须高于教材难度,并且尽量覆盖初中阶段几何核心知识,考查基本图形的典型性质.母题出现在八年级下册,它所涉及的初中几何知识比较少,笔者在此图形的基础上,通过折叠变换改变条件,整合相关性质和图形间关系,以探究相关结论来创编,达到命题预设.
2.1 改变折叠方式,初稿框架稚现
第1稿:四边形ABCD是矩形,P是AB上一点,将△PBC沿PC折叠得到△PB′C,直线CB′与AD交于点E,BE,CP交于点F,DC=6.
(1)如图2,当点A与点P重合时,比较线段AE与DE的大小;
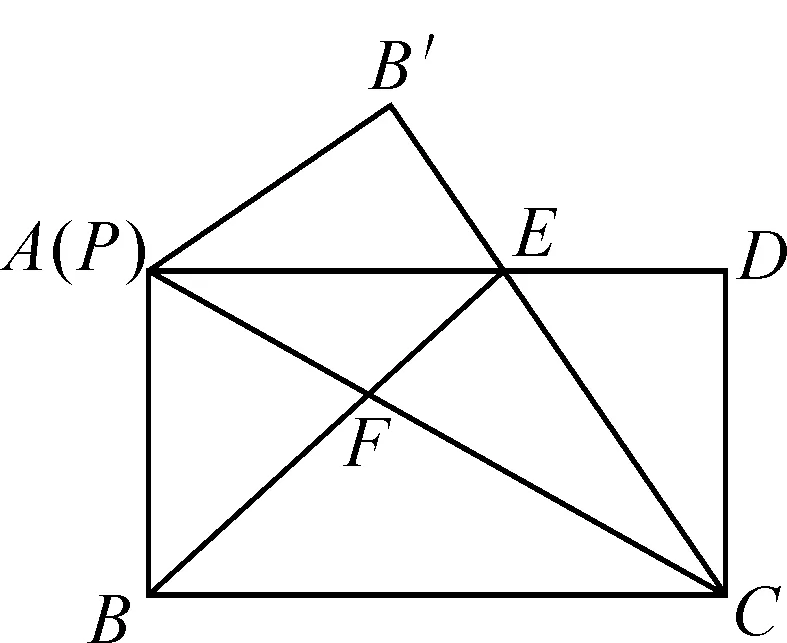
图2
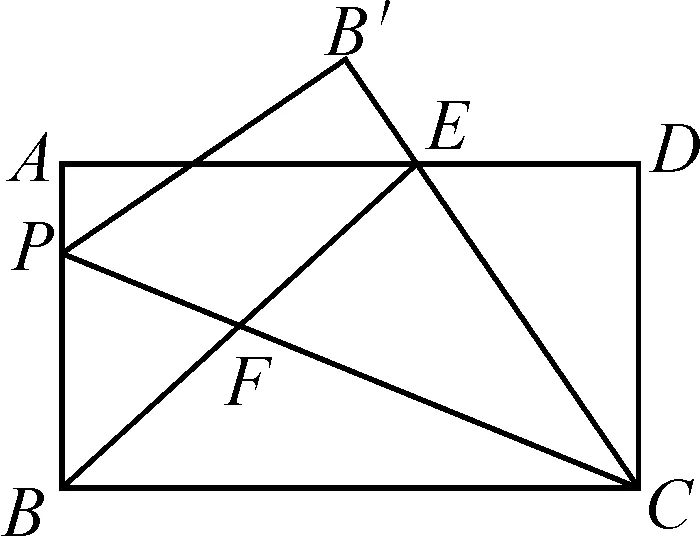
图3
(2)如图3,点P在运动的过程中,有唯一点P使PB′∥BE,求AP∶PB;

图4
(3)如图4,当PB′∥BE时,半径为2的⊙O与△PBC的两边相切,且点O在△PBC的内部或边上,求PB的取值范围.
诊断分析:第(1)问为“比较线段长度大小”这个基本的数学问题,考查折叠的基本性质及直角三角形边角关系,绝大多数学生能解决,体现了试题由易到难的基本特征.第(2)问考点设置比较好,体现了数形结合思想.第(3)问关联圆的知识,突出了对核心知识与方法的考查预设.第1稿出来之后,命题组成员认为“以矩形及矩形折叠为基本条件,将矩形上一点设置为动点,折叠所得图形随动点的移动而变化”为题干的思路比较好.但是,第(2)问入口太窄,方法比较单一,难度偏大,建议将动点改为定点,重新编制题干;第(3)问把圆的知识放进去,感觉比较突兀,导致本道题不流畅、不自然,有拼凑之嫌,同时分类太多致使书写量偏大,不利于考生解答.于是尝试将(3)中“⊙O与△PBC的两边相切”改为“以CF为直径作圆,交DE于点G”,将动圆设置为定圆,以更好地突出考查数学本质,于是得到第2稿.
2.2 精准考查核心, 改造条件设问
第2稿:四边形ABCD是矩形,P是AB上一点,将△PBC沿PC折叠得到△PB′C,CB′与AD交于点E,BE,CP交于点F,PB′∥BE.
(1)如图5,①求证:BP=BF;②E是AD的中点,且AD=nAB,求n的值.
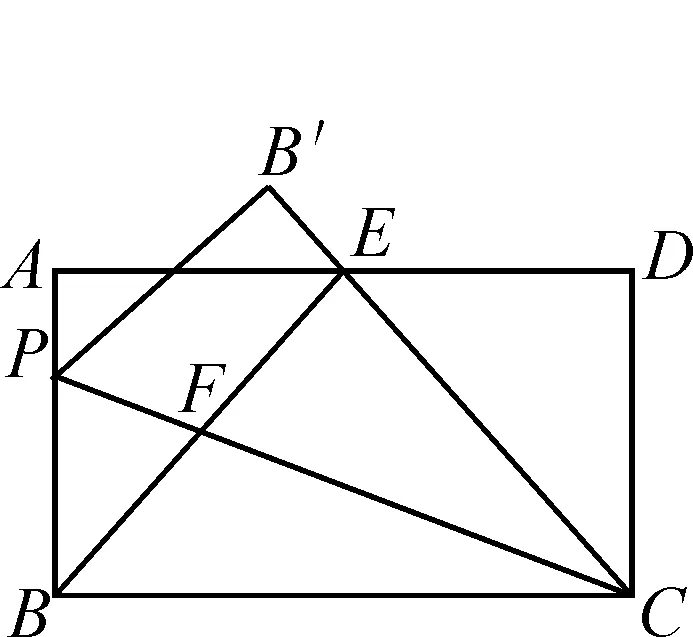
图5

图6

诊断分析:第2稿中,第(1)问中“E是AD的中点,且AD=nAB”不简约,并且条件“AD=nAB”的出现,可能会给学生带来一定的思维障碍;第(2)问设置求“tan∠ECG”,需要学生自己搭桥太多,计算量过大,证三角形相似次数太多,而且方法单一.命题组经过讨论,认为圆在这里出现仍比较牵强,不能突出对核心知识的考查,决定只在直线型中挖掘新的结论,突出对学生解决问题方式的考查.

2.3 优化条件设问,突出运算推理
第3稿:已知矩形ABCD中,P是边AB上一点,把△PBC沿着直线PC折叠,顶点B的对应点是点G,CG交线段AD于点E,连接BE,与线段PC交于点F,且BE⊥CG.
(1)如图7,AE=DE,求证:AD=2AB;

图7
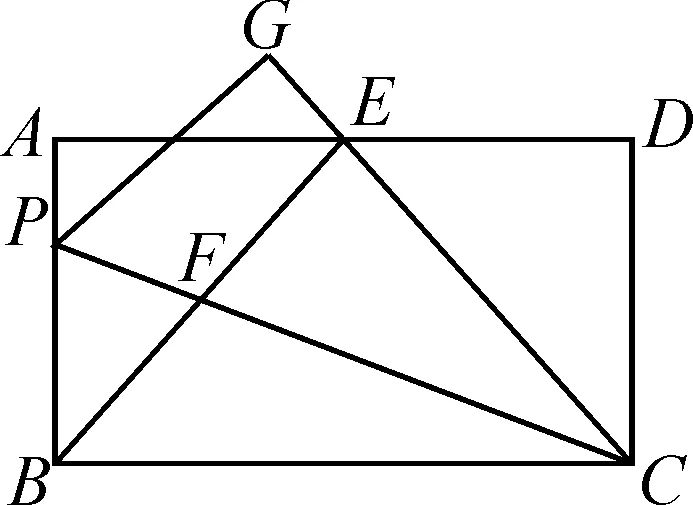
图8
(2)如图8,AE 诊断分析:在讨论第3稿时认为,设置第(1)问的目的,一是考查三角形全等的证明方法,二是为求tan∠PCB的值作铺垫.虽然第(1)问中设置的“求证AD=2AB”的方法较多,有利于考查思维的全面性,但对于本题后续问题的解决有干扰,并且后续第(2)问中的①②问都要用到三角形相似的知识,因此决定将第(1)问直接设置为证三角形全等.第(2)问给的数据为分数,在形式上给学生造成运算的心理负担,于是将条件中的数据设置为整数,给学生以简洁的感觉,体现人文关怀,但是对比本地模拟题中大多是求正切值,①中求tan∠PCB的值存在套路,达不到预期的区分度,因此改为“求cos∠PCB的值”. 确定好题目考查方向后,再次核对课程标准中对应的知识及能力要求,看是否符合命题要求.最后环节是语句的打磨及图形的再构造,确保试题简洁、美观、悦目,确保考查的效度[2],彰显人文关怀.最后得到如下中考数学第23题. 中考稿:在矩形ABCD中,AB=12,P是边AB上一点,把△PBC沿直线PC折叠,顶点B的对应点是点G,过点B作BE⊥CG,垂足为E,BE交PC于F,点E在AD上. (1)如图9,当点E是AD的中点时,求证:△EAB≌△EDC; (2)如图10,①求证:BP=BF; ②当AD=25,且AE ③当BP=9时,BE·EF的值. 图9 图10 诊断分析:本题最终以矩形为背景进行图形变换,以考查几何推理为主,并设问求线段长的乘积及三角函数值等,充分考查学生几何直观、空间想象、逻辑推理和数学运算等核心素养.设问具有关联性,“①求证:BP=BF”,为解决第②问起到搭桥的作用;②中条件“AE 编制本题时,难点定在对数学思维的考查,并在题干及问题设置上渗透人文关怀.精心打磨题干语言,力求与教材中的习题语言的规范性一致,通过多次打磨,降低了学生阅读量,学生不存在阅读障碍;精心搭建桥梁台阶,通过设置递进式问题引导学生思维;精心拓宽解题入口,秉承“人人都有获得数学教育的机会”理念,争取让 “人人都敢于尝试压轴题”,试题解法多样,便于不同水平的考生都能有施展身手的舞台.

2.4 直击数学本质 , 彰显人文关怀


3 命题感悟
3.1 打磨细节,增强考查的效度
3.2 适时反思,着眼核心素养