基于ARIMA-SVM组合模型的电力负荷预测

孟鑫 梁霄

关键词：电力负荷预测；ARIMA; SVM;组合预测

1引言

电力系统负荷在当下能源紧缺的环境中成为各个国家和地区的重要议题。近年来，全球气候呈现以变暖为主要特征的显著变化，极端气候事件发生的概率和强度不断上升。天气系统复杂多变和社会事件（政策变化、节假日、电网故障、经济活动、疫情影响等）等不确定因素给准确的预测带来困难，选择合适的预测算法成为研究电力负荷的关键。

电力系统负荷可以由线路中设备总功率求和得到，根据用户的用电习惯和生活工作规律，电力负荷会随时间产生一定的规律性变化，符合时间序列的基本特征。电力系统负荷时间序列具有复杂性、不确定性、非线性等特征，由于受到复杂多变的气候和能源供应链等可变性因素影响，其数据包含线性和高度非线性特征，这导致电力系统负荷预测难度较大。目前，电力负荷传统预测模型主要关注数据的时序性特征而忽略了数据存在的非线性特征。我们希望构建一种既能反映数据的时间序列特征，又能体现出数据的非线性属性的模型，于是本文重点将ARIMA模型和SVM模型进行组合优化，对电力负荷的预测进行研究。

2基本模型

2.1ARIMA模型

ARIMA模型是研究时间序列的一类经典统计模型，在處理线性问题上有巨大优势[1]。ARIMA模型的本质是将不平稳的时间序列经过差分使原始数据平稳化后再对其建立自回归和滑动平均模型（ARMA）。构建和预测模型之前需要对数据进行平稳化处理，通过参数估计方法得到残差最小化的模型。ARIMA（p，d，g）模型的设定如下[2]：其中，L是滞后算子，表示残差序列。

2.2SVM模型

支持向量机方法是一类在解决非线性问题上有许多特有优势的机器学习算法，由Vapnik等首先提出，其基本原理是根据统计学VC理论的系统问题最小化原则，对特定训练样本的训练精度与学习质量关系的折中，以期望模型显示出最佳的泛化水平[3]。

2.3ARIMA－SVM组合模型

ARIMA模型和SVM模型分别在处理线性和非线性问题上具有各自的优点和特色[4]．因此本文将二者结合起来构建组合模型，对电力负荷进行预测，以期望取得较好的预测效果。在数据线性规律由ARIMA模型捕捉的基础上，提取ARIMA拟合模型的残差序列作为构建SVM模型的训练样本，用编程语言循环搜寻残差最优化的参数，让SVM算法捕捉到数据的非线性趋势，形成组合模型，最终的预测值由ARIMA和SVM预测的结果相加得到。

2.4评价指标

为了验证组合模型在电力负荷预测中的有效性，本文选择ARIMA和SVM为参照模型，同时为了便于模型预测和模型评价，本文中三种模型的预测方法均采用一步预测法，并且所有模型均基于R语言编程实现。为了更有效地反映模型的优劣性，本文结合均方根误差（RMSE）和平均绝对误差百分比（MAPE）来评价组合模型的预测效果。RMSE和MAPE的计算公式如下[5]：

3电力负荷预测仿真

3.1数据来源

本文采用的数据整理自广东省某市2018年1月1日0：00—2018年1月14日23：45电网间隔15分钟的负荷数据，该时间段内该市无极端气候和能源供应等不稳定性影响，时间序列内没有异常变化。选取数据中前13日的负荷数据（共1248个数据），并划分为训练样本进行模型拟合和预测，14日的负荷数据划分为测试样本，以验证拟合模型的优劣。图1为前13日共1248个电力负荷数据的变化图，由图1可见数据的周期性特征较为显著。

3.2电力负荷预测及拟合效果

3.2.1ARIMA模型建立及预测

首先对原始日寸间序列进行预处理，依据拉依达准则，借助R语言boxplot（）函数画出数据箱线图，观察得到数据中无异常值，原始数据可直接进行建模。利用R语言中的unitrootTest（）函数检验电力负荷数据的单位根，从而判断数据是否为非平稳时间序列。若数据无法通过单位根检验，则可以利用差分对数据进行变换。单位根检验结果如表1所列，其中单位根检验P值小于0.05，说明数据为非平稳时间序列。

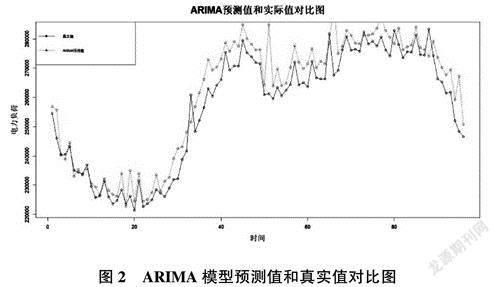
原始时间序列经过一阶差分后通过了单位根检验，并且有99%的置信度。可以认为一阶差分序列为平稳序列，因此设定ARIMA模型参数d=1。借助R语言中的auto. arima（）函数来选择模型AIC和BIC中最小的参数p，g，得到拟合的最优模型为ARIMA（5，1，1）（0，1，0）[96]。此时，拟合模型的AIC=23 514.47。由ARIMA模型预测值和真实值在图2中的对比可知，模型捕捉日寸间序列数据的线性特征较为充分。

3.2.2SVM模型预测

将训练集中前12天的数据作为输入，第13天的数据作为输出，选取径向基核函数作为核函数进行拟合模型，这是一个基于样本点之间的距离决定映射方式的函数，径向基核函数属于局部核函数，当数据点距离中心点变远时，取值会变小。高斯核函数的形式如下：

由拟合的ARIMA模型可知，时间序列周期为96，将2018年1月1日～2018年1月13日的电力负荷ARIMA模型预测值残差使用SVM模型进行拟合，寻求到最优SVM模型参数拟合模型进行预测，在数据线性规律由ARIMA模型捕捉的基础上，提取ARIMA拟合模型的残差序列作为构建SVM模型的训练样本，用编程语言循环搜寻残差最优化的参数，让SVM算法捕捉到数据的非线性趋势，形成ARIMA-SVM组合模型，最终的预测值由ARIMA和SVM预测的结果相加得到。由图3可知，组合模型的预测值能够更好地拟合电力负荷的实际值，主要原因是组合模型很好地利用了两种模型的优势，充分提取数据特征。

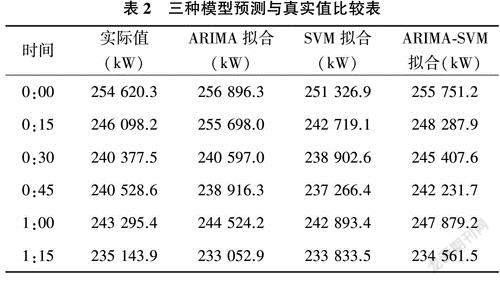
三种模型部分预测值（1月14日）如表2所列，可以发现ARIMA-SVM预测值最为接近真实值。

3.3模型评价

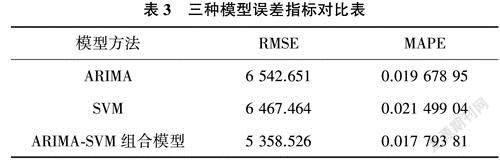
根据上述三个模型的预测值和实际值进行误差指标计算，得到模型预测的均方根误差（RMSE）和平均绝对误差百分比（MAPE）的结果，如表3所列。SVM模型的预测值偏差略优于ARIMA模型．ARIMA模型的预测值偏离度优于SVM模型，这表明时间序列中的线性因素和非线性因素对模型预测的影响相当，而组合模型的预测误差和偏离度均优于单一模型，充分证明本文ARIMA-SVM组合模型能够最大限度地提取数据的时间序列特征和数据的非线性属性，并大幅提高预测精度。

4结束语

本文利用ARIMA模型捕捉电力负荷数据中的线性趋势，结合SVM算法预测数据的非线性趋势。基于广东某市电力负荷数据的算例分析表明了ARIMA-SVM组合模型在预测具有非线性特征的时间序列中的准确性。线性与非线性高度结合的ARIMA-SVM组合模型可以成功应用到电力负荷时间序列预测模型中，通过更全面地挖掘数据中蕴含的信息，构建出更加系统和准确的模型，从而提升预测效果。