多点支撑结构形变及轴系轴承承载性能分析

牛荣军， 刘越，唐红利，崔永存，邓四二

(1.河南科技大学 机电工程学院， 河南 洛阳 471003； 2.北京理工大学 机械与车辆学院， 北京 100081；3.中国北方车辆研究所， 北京 100072)

0 引言

多点支撑轴系轴承广泛应用于发动机、变速箱、机床主轴等机械传动机构中，其性能优劣直接影响到机械系统的运动平稳性、旋转精度和寿命等。随着高功率密度传动系统性能的提升要求，轴系轴承高承载、长寿命的指标也不断提高[1]。目前，在多点支撑轴系轴承的性能评估中仍多采用将支撑轴视为刚性的简化方法进行估算[2-5]，其结果一般会高估轴承性能，给主机的安全运维带来隐患。因此，考虑多点支撑结构的形变影响，进而优化轴系结构配置，提升轴系轴承综合疲劳寿命为高功率传动系统的研发提供理论依据，极具现实意义。

关于滚动轴承的承载能力，国内外学者已开展了较为深入的研究。刘越等[6]针对传动系统中典型的多轴承支撑轴系结构，提出了轴和轴承刚度耦合建模方法以及轴系结构精确变形迭代求解方法，获得了轴系的精确变形。罗祝三等[7]提出了考虑轴的弹性变形对多支点轴系中若干滚动轴承联合进行拟静力学分析的模型，分析结果表明设计中要考虑轴系变形轴承的影响。田程等[8]针对多支撑轴系分析的难点，提出了一种考虑轴承刚度耦合性和非线性的有限元计算方法。倪艳光等[9]基于有限元建模方法，分析了套圈变形对球轴承载荷分布以及刚度、寿命等力学性能的影响，结果表明薄壁球轴承要充分考虑套圈变形与支撑配合关系的影响。毛宇泽等[10]通过求解包含套圈弹性变形的非线性方程组，分析了负游隙对轴承承载性能及疲劳寿命的影响。Sun等[11]建立了鼠笼式柔性支承滚动轴承的准动态迭代有限元分析模型，计算并分析了整体柔性支撑结构对滚动轴承内部载荷分布和动态特性的影响。李云峰等[12]建立了包含支撑结构刚度的轴承静力学分析模型，分析了轴承游隙及初始接触角对轴承承载能力的影响，并验证了模型的正确性。Lacroix等[13]对薄壁四点接触球轴承的载荷- 位移特性进行了实验研究，并比较了考虑和不考虑套圈刚度时的试验和数值结果。王亚珍等[14]建立了考虑薄壁套圈变形的滚子轴承拟静力学分析模型，得到不同工况下的轴承载荷分布和疲劳寿命。Harris等[15]利用圆环的变形方程与Hertz接触变形公式建立了一组柔度方程组，对具有弹性外圈的行星齿轮轴承的载荷分布进行了分析。刘宏等[16]对鼠笼式弹性支撑件下的齿轮接触性能进行了试验研究，发现鼠笼式弹性支承件的支撑刚度对齿面接触区和传动误差有较大的影响。邓四二等[17]研究了沟槽式弹性支撑结构参数对双半内圈角接触球轴承动力学特性的影响，指出合理选择弹性支撑结构参数可有效改善轴承的动态性能。毛月新[18]等研究了滚子凸度设计及修形对轴承接触载荷特性的影响，但没有定量给出修形对轴承疲劳寿命的影响。

综上所述，在多点支撑轴系中，由于转动支撑轴的挠曲变形，以及轴承多点支撑刚度影响，使得轴系轴承的力学性能发生明显变化，如果还采用常规的轴承设计分析方法，则轴承的承载能力和寿命将产生明显误差，不符合实际工程应用情况。

本文基于弹性力学的Timoshenko梁单元理论建立多点支撑轴系的通用力学模型，并耦合轴系轴承刚度的影响，系统研究了传动轴系驱动力矩大小、作用位置和配置参数等对轴系轴承的承载性能影响，以期为轴系结构的优化配置提供参考依据。

1 多点支撑轴系的力学模型建立

为详细考察多点支撑轴系中支撑轴系挠曲变形和轴系轴承刚度复合对轴承承载性能的影响，下面基于一般通用的轴系多点支撑结构，采用弹性力学的Timoshenko梁单元理论建立多点支撑轴系分析模型，然后耦合轴系轴承刚度进行多点支撑轴系轴承的力学性能研究。

图1所示为多点支撑轴系受载的通用力学模型示意图，支撑轴系中包括支撑轴承和传递齿轮等部件，支撑轴与各个轴系轴承支撑可以视为承受轴向载荷、径向载荷及力矩的弹簧。定义坐标系Oxyz原点O位于支撑轴轴线上，第1列轴系轴承中心到原点的轴向距离为l1，第j(j=1,2,…,m,m表示轴系轴承的总列数)列轴系轴承中心到原点的轴向距离为lj；各轴系轴承在x轴和y轴方向的径向载荷分量分别为Fjx、Fjy，在z轴方向的轴向载荷为Fjz；在x轴和y轴方向的力矩分量分别为Mjx、Mjy；作用于支撑轴系上的各外部载荷到坐标原点的轴向距离分别为a1，a2,…,ai，…，an(n表示外力作用位置标号)；各外部载荷在x轴、y轴和z轴方向的分量分别为p1x～pnx、p1y～pny和p1z～pnz；在x轴和y轴方向的力矩分量分别为T1x～Tnx和T1y～Tny。

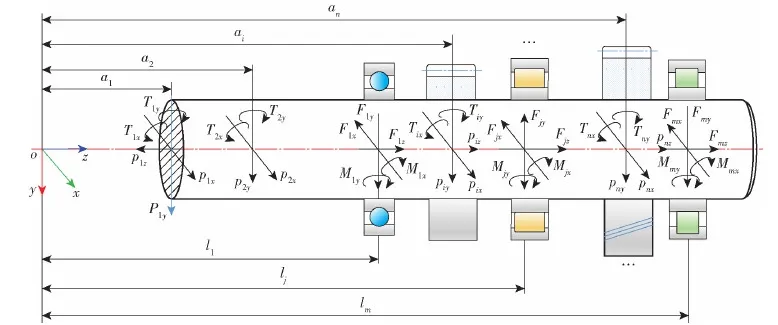
图1 多点支撑轴系受载力学模型Fig.1 Mechanical model of a loaded multi-point support shaft

依据图1所示支撑轴系受力作用关系，可以列出支撑轴系的力平衡方程式：

(1)

(2)

(3)

(4)

(5)

1.1 支撑轴系挠曲变形计算

支撑轴系的转角和挠度分别以α和ω表示，根据弹性力学理论，在图1所示的轴系中支撑轴挠曲的微分方程为

(6)

式中：M为作用弯矩；EI表示支撑轴的抗弯刚度，E为弹性模量，I为惯性矩。

采用积分法可得支撑轴系在分析区间内的转角和挠度方程：

(7)

(8)

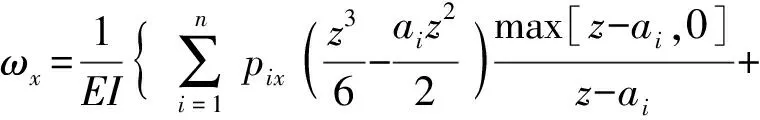
(9)

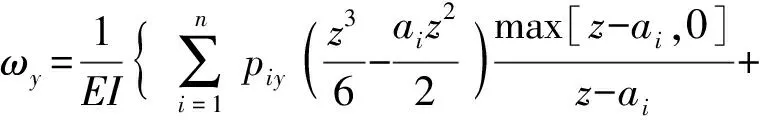
(10)

式中：C1j～C4j为积分常数；下标x、y表示沿x轴、y轴方向。

1.2 边界条件确定

根据变形协调原则，在各支撑轴系轴承的中心截面处，支撑轴的形变与轴系轴承支撑位置处的形变应协调一致。因此，参照图1多点支撑轴系模型，可以列出轴系轴承支撑位置的边界条件：

当z=l1时，

(11)

当z=lj时，

(12)

当z=lm时，

(13)

式中：θ和δ分别为各列轴系轴承中心截面位置处的转角和位移变形量。

将边界条件式(11)～式(13)代入式(7)～式(10)，可以确定积分常数C1j～C4j以及轴系第j轴承列中心截面位置处的转角和位移关系式。

2 轴系轴承力学模型建立

本文所分析的轴系结构中有QJ309四点接触球轴承、MU209圆柱滚子轴承和MU2306圆柱滚子轴承3个典型型号。选择QJ309和MU2306进行力学建模分析，型号MU209与MU2306的推导方法相似。

根据变形协调原则，各轴系轴承的形变与对应支撑轴截面中心的形变协调一致。因此可以用各轴系轴承支承点位置对应的支撑轴截面中心形变量对轴系轴承进行受载形变分析，即支撑轴和轴系轴承形变量相同。这里给出沿着y轴方向径向变形和绕x轴倾斜变形的分析过程，沿着x轴方向径向变形和绕y轴倾斜受载变形可同理分析。轴系轴承中滚动体编号和位置角的设置如图2所示。图2中，Z为滚动体个数，ψk表示各个滚动体的分布位置角，k表示滚动体编号。

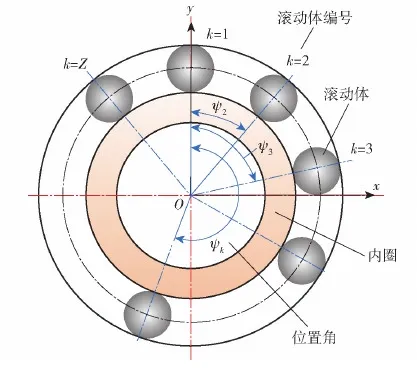
图2 滚动体编号及位置角定义Fig.2 Numbering and position angles of rolling elements

2.1 轴系圆柱滚子轴承位移变形分析

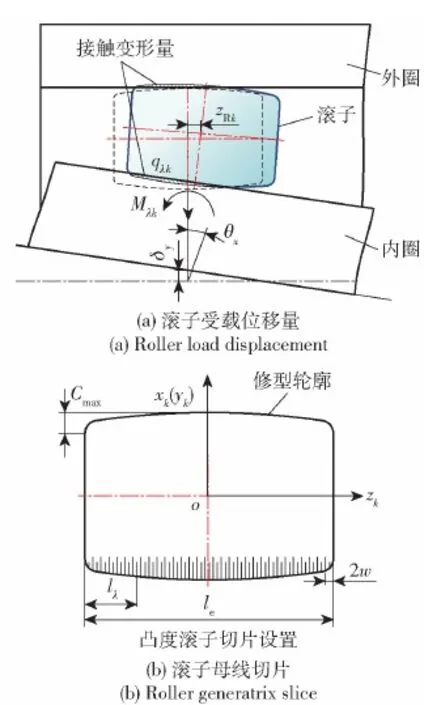
图3 滚子与滚道接触关系Fig.3 Contact relationship between roller and raceway

本文研究的轴系结构的中间和右侧端为圆柱滚子轴承。对轴系圆柱滚子轴承进行分析时，为了考虑因支撑轴挠曲变形造成轴承滚子倾斜对接触状态的影响，采用切片法沿滚子母线进行离散化处理，切片的宽度为2w=le/N(le为滚子的有效长度，N为切片总数)。图3为滚子与滚道接触关系示意图，其中lλ为(λ为切片编号)每个切片到滚子左参考面的距离，Cmax为滚子凸度量，Mλk为每个切片对滚子中心产生的力矩，qλk为每个切片产生的接触载荷，θx为内圈绕x轴的转角，δy为内圈在y轴方向的径向位移量，zRk为滚子中心倾斜产生的轴向位移量，下标R表示轴系圆柱滚子轴承列。

考虑滚子倾斜、游隙和凸度修型等影响，沿着滚子母线方向，每个滚子切片单元与滚道间产生的接触变形量为

δykλ=δycosψk+θxcosψk(0.5le-lλ-zRk)- 2cλ-uRr

(14)

式中：lλ=w[1+2(λ-1)]，1≤λ≤N；cλ为滚子凸型的修型量；zRk=0.5dmtan(0.5θxcosΨk)，dm为轴承节圆直径；uRr为轴承的径向游隙。

考虑滚子修型影响，每个滚子切片单元与滚道间的接触力及力矩分别为

(15)

(16)

接触力和力矩在y轴方向的径向力和绕x轴的力矩分量分别为

(17)

(18)

式中：Zr为滚子个数。

同理可求出接触力和力矩在x轴方向的径向力和绕y轴的力矩风量分别为

(19)

(20)

式(14)～式(20)中，下标x、y分别表示图2所示坐标系中沿y轴方向和绕x轴。

2.2 轴系球轴承位移变形分析

本文研究的轴系支撑结构中左侧为QJ309球轴承，滚动体与滚道间设计为四点接触，根据需要也可设计为两点或三点接触球轴承。钢球与沟道间的弹性变形量可通过内、外沟道的曲率中心距变化来分析。图4为四点接触状态时钢球与沟道接触关系图。图4中，O′为受载后球心位置，α0为设计接触角，δz为内圈在z轴方向的径向位移量，c1ik为受载前接触对Ⅰ内曲率中心，c2ik为受载前接触对Ⅱ内曲率中心，c′1ik为受载后接触对Ⅰ内曲率中心，c′2ik为受载后接触对Ⅱ内曲率中心，c1ek为受载前后接触对Ⅰ外曲率中心，c2ek为受载前后接触对Ⅱ外曲率中心。

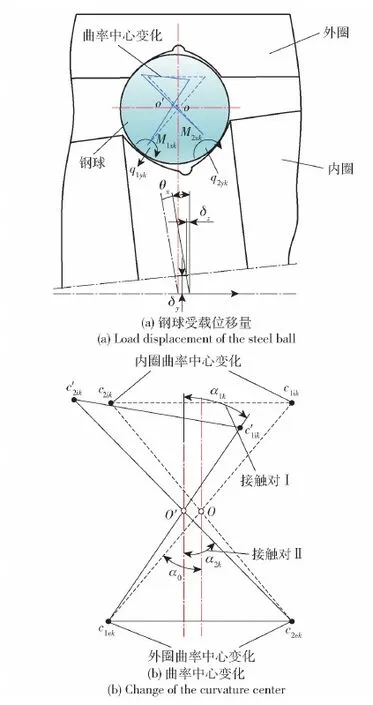
图4 钢球与沟道的接触关系Fig.4 Contact relationship between steel ball and raceway

受载后，各个位置角处钢球与内、外沟道的接触弹性变形量为

δ1yk=[(A0sinα0+δz+Riθxcosψk-uBa)2+

(A0cosα0+δycosψk-uBr)2]0.5-A0

(21)

δ2yk=[(A0sinα0-δz-Riθxcosψk-uBa)2+

(A0cosα0+δycosψk-uBr)2]0.5-A0

(22)

式中：A0为内外沟道初始曲率中心距；α0为设计接触角；Ri为内圈沟曲率中心圆半径；uBa为轴向游隙；uBr为径向游隙。

各个位置角处钢球- 滚道间的接触角为

(23)

(24)

依据赫兹接触理论，两个接触对产生的接触载荷分别为

q1yk=Kn[max (0,δ1yk)]1.5

(25)

q2yk=Kn[max (0,δ2yk)]1.5

(26)

式中：Kn为钢球与沟道的接触变形系数，可参考轴承设计理论[19]确定。

接触载荷对内圈产生的沿z轴方向轴向力、沿y轴方向径向力和绕x轴的力矩分别为

(27)

(28)

(29)

式中：Zb表示钢球个数。

同理，可得到接触载荷对内圈沿着x轴方向径向力和绕y轴的力矩分别为

(30)

(31)

联立式(1)～式(5)、式(17)～式(20)和式(27)～式(31)，可得到轴系轴承共21个未知量的非线性方程组。本文采用Newton-Raphson方法对所建立的非线性方程组进行迭代数值求解，求解误差设置为10-6，最终得到轴系轴承的位移、转角变形量以及支撑轴的挠曲变形等，进而得到轴系轴承的载荷分布、接触角和寿命等性能参数。

3 计算结果及分析

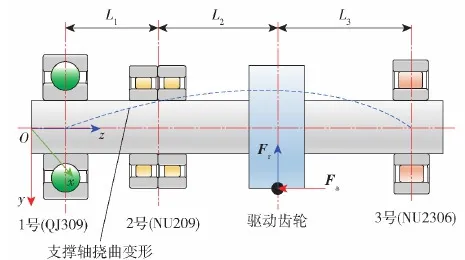
图5 多点支撑轴系轴承配置Fig.5 Multi-point support shafting bearing configuration

某变速箱驱动轴系轴承的具体多点支撑轴系结构和轴承配置如图5所示，结构参数如表1所示。中间驱动齿轮的力矩T为800 N·m，轴系轴承和驱动齿轮的位置L1为40.5 mm、L2为52.5 mm，L3为51.5 mm，Fr为斜齿轮所受径向力的合力，Fa为斜齿轮轴向力。

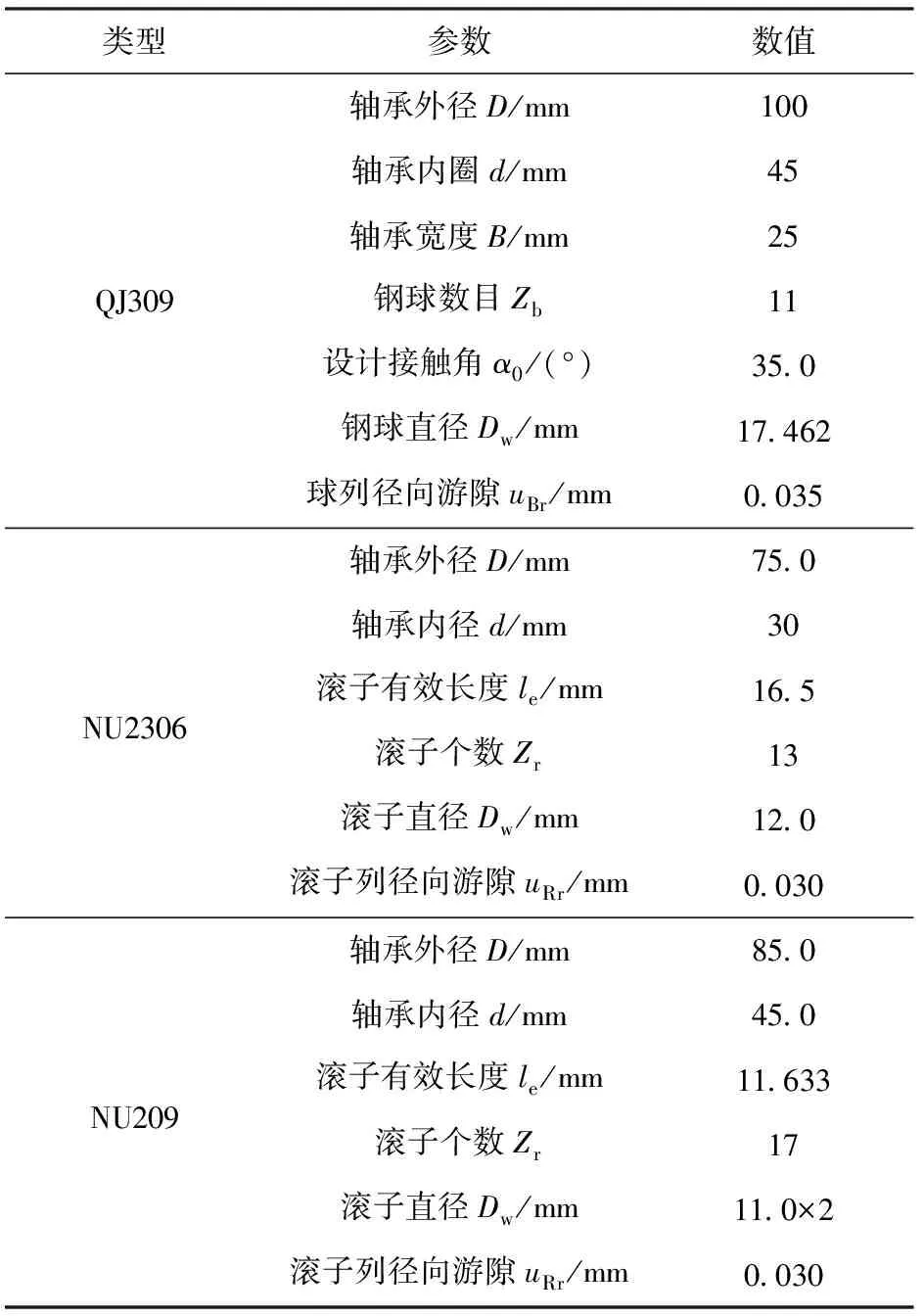
表1 轴承类型和结构参数Table 1 Parameters of bearing type and structure

下面通过驱动力矩大小、载荷作用位置和安装配置等研究支撑轴的挠曲变形对轴系轴承的载荷分布、接触角和爬坡率等影响，评估多点支撑轴系轴承的承载性能。

3.1 刚柔多点支撑轴系刚性比较

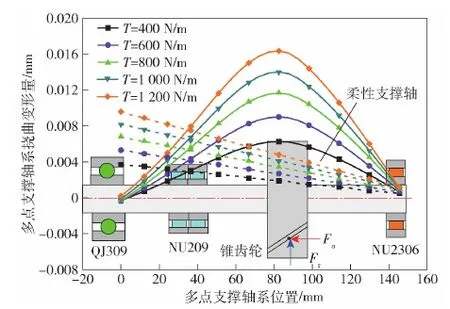
图6 多点支撑轴系形变刚性比较Fig.6 Comparison of rigidity of multi-point support shafting

为表明多点支撑轴系中，刚性和柔性支撑轴对轴系轴承承载性能的影响，图6给出驱动力矩T在400～1 200 N·m范围变化时支撑轴的挠曲变形影响对比。

由图6可以看出：

1)随着驱动力矩的增大，刚性轴不能产生挠曲变形，只能通过偏转角的改变，调节多点支撑轴系轴承的载荷比分配，使得左端球轴承的径向变形明显增加，具体刚性变形见表2的数据结果；

2)随着驱动力矩的增大，柔性轴的挠曲变形明显，特别是中间齿轮作用位置，变形量最大。由于考虑多点支撑轴挠曲变形的影响，使得多点支撑轴系轴承的变形量明显不同于刚性轴变形的影响。特别是球轴承的径向变形呈负位移变化，明显不同于刚性轴的正位移变化。具体数据结果如表2所示。

多点支撑轴系中，支撑轴的挠曲变形对各个轴系轴承的载荷分配产生明显影响，采用常规的刚性轴分析方法，将使得轴承寿命评估过于偏大，在实际多点支撑轴承计算中，要考虑支撑轴系的挠曲变形和轴系轴承的耦合作用。

3.2 轴系轴承性能分析

3.2.1 圆柱滚子轴承性能分析

为表明支撑轴系挠曲变形对轴承接触性能的影响，图7给出了多点支撑轴系形变对中间和右端轴系轴承不同修型滚子接触状态的影响结果，选用常用的两边弧坡和对数两种滚子修型方法，为体现对比性滚子凸度量都取为0.08 μm，驱动力矩为800 N·mm，其他参数见表1。

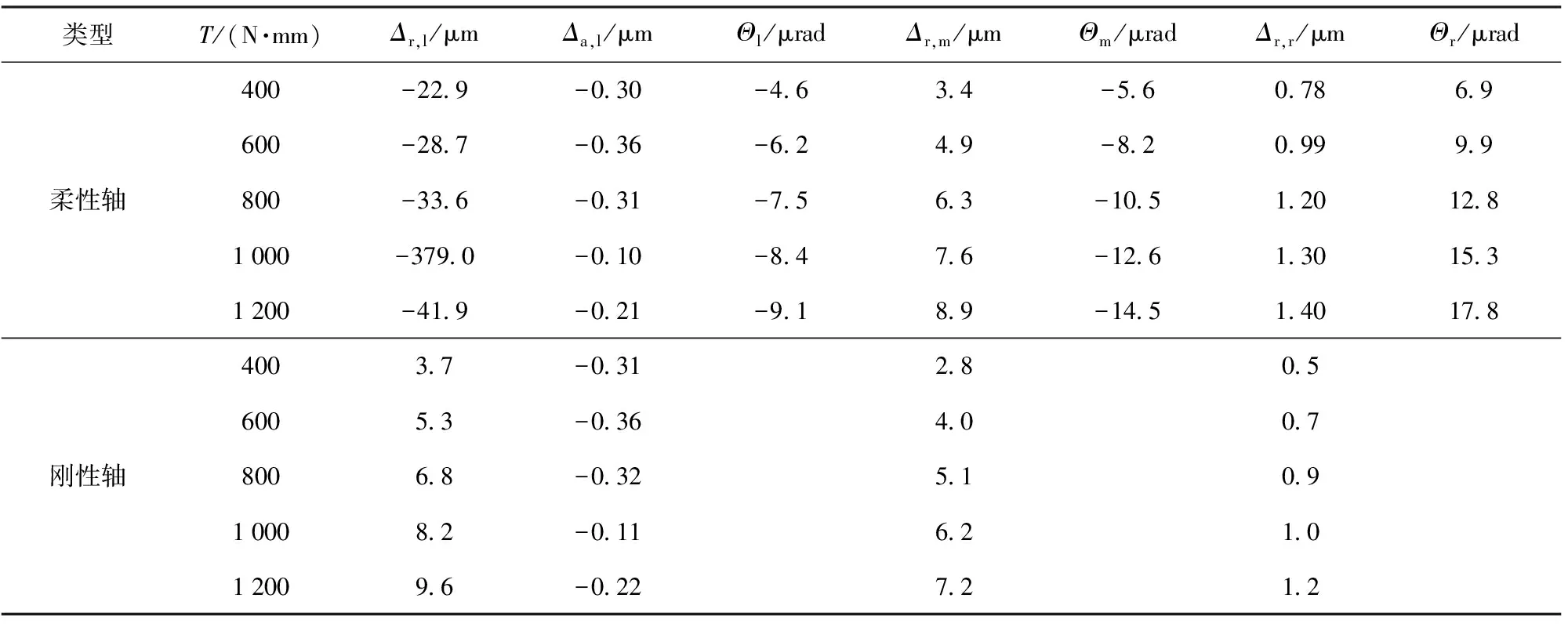
表2 刚柔性支撑轴系对轴系轴承支撑刚性的影响Table 2 Influence of rigid and flexible shafting on support rigidity of shafting bearing

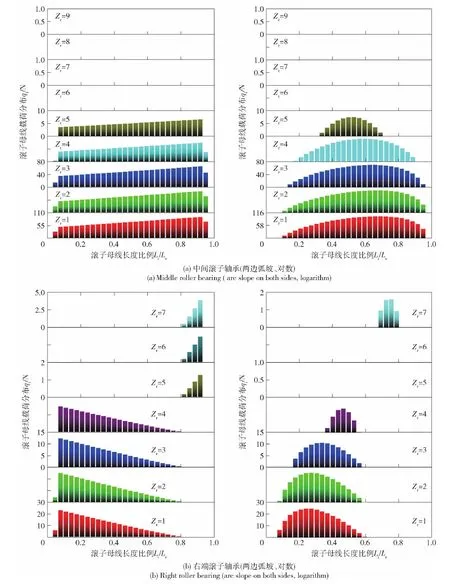
图7 滚子凸型对轴承接触性能的影响Fig.7 Effects of roller crown on contact performance

参照图5轴系坐标系设置。为便于后续轴承受载分析，设置齿轮径向合力方向为y轴方向，此时所分析轴系轴承载荷分布关于yz平面对称，在图7中只提取轴承的一半滚子进行受载分析。由图7中2种滚子修型的结果可以看出：1)柔性轴系对轴承的承载状态产生明显影响，柔性轴由于在轴承支撑点的挠曲变形，对支撑点轴承产生附加力矩作用，使得其母线接触压力分布呈明显的两端非对称状态；2)柔性轴系下，2种修型滚子母线的压力分布区域都明显减小，受载压力均匀性变差，从而造成滚子母线局部承载压力偏大，轴承容易因局部受载压力过大发生早期疲劳失效。

从支撑轴系对轴承的压力分布影响可以看出，多点支撑轴系轴承的分析中，要考虑支撑轴挠曲变形对轴承承载性能的影响，在刚性轴系下轴承受载均匀性要优于柔性支撑轴系，从而过高估计轴系轴承的承载能力，给安全性设计带来一定风险。

图8给出了考虑多点支撑轴系挠曲变形，滚子不同修型方法对中间和右端圆柱滚子轴承载荷分布的影响。

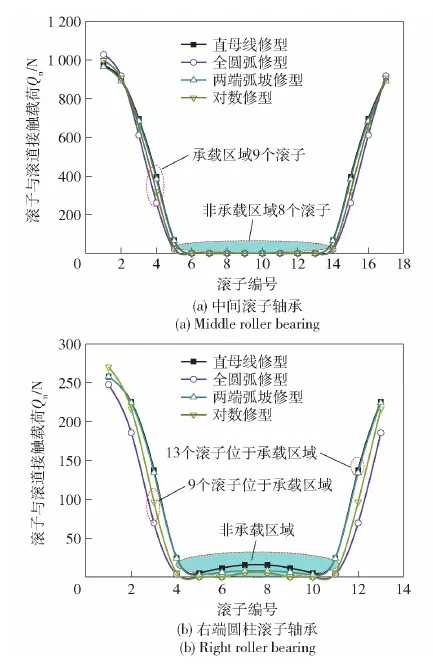
图8 滚子凸型对轴承载荷分布的影响Fig.8 Effects of roller crown on load distribution

由图8可以看出：1)中间圆柱滚子轴承有9个滚子在承载区域，8个在非受载区域，全圆弧修型滚子受载的最大载荷较大，而两端弧坡修型滚子受载的最大载荷最小；2)右端滚子轴承中，对数和全圆弧修型滚子有9个滚子在承载区域，而直母线和两端弧坡修型滚子全部13个滚子承载，其中全圆弧修型滚子受载的最大载荷最小，而对数修型滚子受载的最大载荷最大。

根据多点支撑轴系中间和右端滚子轴承受载特点分析，中间滚子轴承选择两边弧坡修型、右端滚子轴承选择全圆弧修型比较合适，有助于降低轴承的受载压力，延长轴承使用寿命。

图9给出了多点支撑轴系中，驱动力矩T在 400～1 200 N·m范围变化时对中间和右端滚子轴承载荷分布和最大接触压力的影响。

图9 驱动力矩对轴承承载性能的影响Fig.9 Effects of driving torque on the bearing performance

由图9可以看出：1)随着驱动力矩的增大，分配到中间和右端圆柱滚子轴承的作用载荷增加，使得滚子轴承的载荷分布都整体增大；2)中间圆柱滚子轴承的受载载荷明显高于右端圆柱滚子轴承受载载荷，需适当调整齿轮力作用位置，使得中间和右端滚子轴承受载尽量相同、寿命接近，达到同寿命设计；3)多点支撑轴承系轴承中，中间和右端圆柱滚子轴承最大接触压力都呈现不断增加趋势，其中内圈接触压力明显高于外圈接触压力，使得轴承内圈要早于外圈发生疲劳失效。

3.2.2 四点接触球轴承性能分析

图10给出了驱动力矩T在400～1 200 N·m范围变化时对左端四点接触球轴承载荷分布的影响。

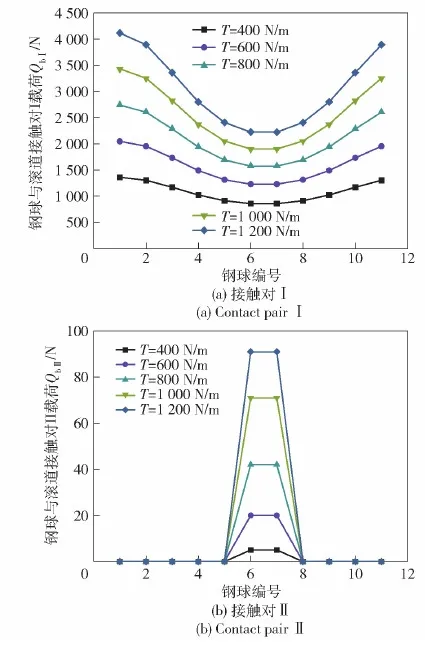
图10 驱动力矩对轴承载荷分布的影响Fig.10 Effects of driving torque on load distribution

由图10可以看出：1)随着驱动力矩的增大，分配到左端四点接触球轴承的作用载荷增加，使得球轴承的载荷分布都整体增大；2)由于球轴承的多点接触特点，部分钢球存在两个接触对同时受载情况，钢球编号6和7同时受载。由于其多点受载作用，钢球的运动灵活性受到限制；3)接触对Ⅰ起主要受载作用，其载荷分布明显高于接触对Ⅱ的承载载荷。接触对Ⅱ整体受载较小，大部分钢球处于非承载状态，因此在多点支撑轴系中，球轴承主要承受轴向和力矩载荷，分配到球轴承的径向载荷较少。

图11给出了不同设计接触角对左端四点接触球轴承接触角和接触压力的影响。

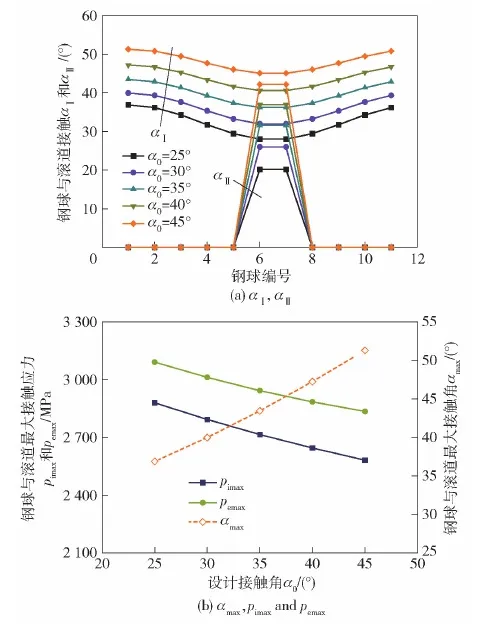
图11 设计接触角对轴承接触性能的影响Fig.11 Effects of design contact angle on bearing contact performance

由图11可以看出：1)设计接触角的增大，有助于四点接触球轴承抵抗轴系分配的轴向载荷，降低轴承接触载荷，接触角每增加5°接触最大接触压力下降50 MPa左右；2)在工况条件不变条件下，通过增大设计接触角可以明显减小轴承的最大接触压力，有助于提高轴承抗疲劳失效能力，是延长轴承寿命的有效设计方法。

上述分析表明，接触角变化对提高轴承承载能力，延长轴承寿命具有明显作用，但过大的设计接触角有可能导致接触轴肩爬坡率过高，造成轴承爬坡问题[20]，从而造成轴承在轴肩位置过早失效风险。因此，要合理选择初始设计接触角，在极限载荷作用下轴承不出现爬坡问题，原理图如图12所示，其中ci为内圈沟道曲率中心。

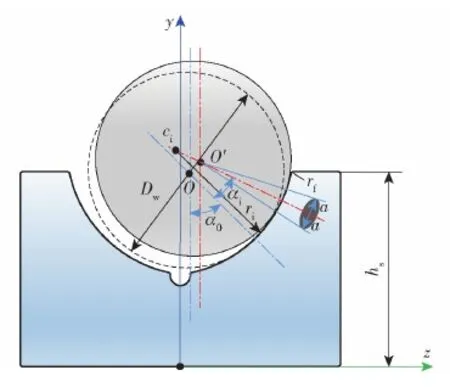
图12 球轴承轴肩爬坡原理图Fig.12 Schematic diagram of ball-bearing shoulder climbing

内圈最小挡边高为

(32)

外圈沟道的最小挡边高为

(33)

内、外圈爬坡率定义为

(34)

式中：ri为内圈沟道的曲率半径；re为外沟道曲率半径；α为实际接触角；θ为内圈受载后的转角；ai为内圈接触椭圆的长半轴；ae为外圈接触椭圆的长半轴。

图13为在设计接触角为35°，驱动力矩在 400～1 200 N·m范围变化时对轴承爬坡率的影响结果。图14为在驱动力矩为800 N·m，初始设计接触角在25°～45°范围变化时对轴承爬坡率的影响结果。

图13 驱动力矩对轴承爬坡率的影响Fig.13 Effects of driving torque on climbing rate

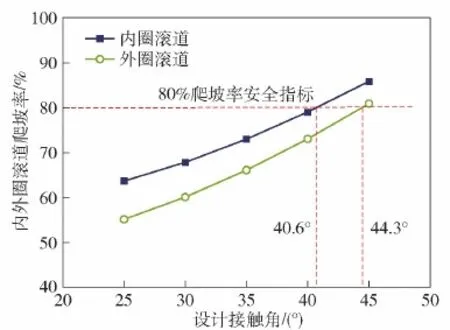
图14 设计接触角对轴承爬坡率的影响Fig.14 Effects of contact angle on climbing rate

由图13可以看出：1)随着驱动力矩的增加，轴承内外沟道的爬坡率非线性增加，内沟道的爬坡率明显高于外沟道爬坡率，因此内沟道出现爬坡失效分析更大，要严苛控制设计接触角的选择；2)设计接触角为35°时，根据80%爬坡率安全指标要求，其驱动轴极限输入力矩1 004 N·m；3)在驱动轴力矩一定工况下(本文研究对象取800 N·m)，内沟道极限设计接触角为40.6°，外沟道极限设计接触角为44.3°。

3.3 齿轮作用位置对多点支撑轴系变形刚性影响

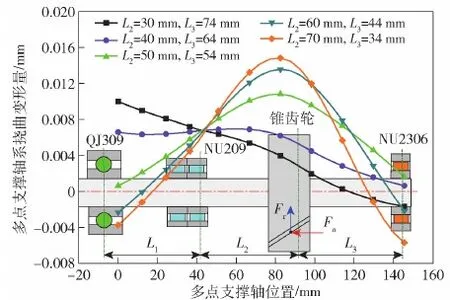
图15 齿轮作用位置对支撑轴系变形刚性的影响Fig.15 Effects of gear action position on rigidity of shafting

为优化所研究多点支撑轴系轴承的载荷分配，提升轴系轴承的承载能力和寿命，图15给出变换驱动力矩T的作用位置，考察支撑轴的挠曲变形特性，并以轴系轴承综合寿命为判断依据(见图16)，从而得到齿轮安装最佳作用位置。

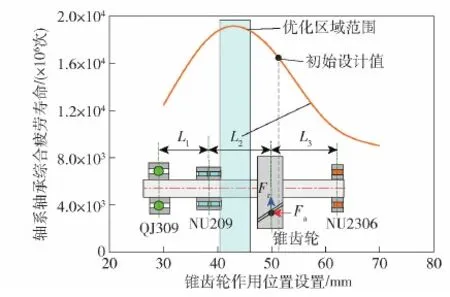
图16 齿轮作用位置对轴系轴承综合寿命的影响Fig.16 Effects of gear action position on life of shafting bearing

由图15和图16可以看出：1)随着驱动力矩T作用位置右移(见图15)，左端球轴承变形由正位移向负位移转变，中间滚子轴承位移变化量不大，右端滚子轴承由负位移到正位移，再到负位移变化；2)依据轴承疲劳寿命理论，计算多列轴承组的综合疲劳寿命(见图16)，可以看出在距离L2为41～46 mm范围，轴系轴承的综合寿命L10处于最大区间，L2过小或过大，轴承寿命呈明显下降趋势。

原始设计中驱动力矩T的位置距离L2=52.5 mm，由图16可以看出，此时轴承寿命处于下降位置，需根据优化结果使齿轮位置左移，适当减小L2长度，增大轴系轴承组综合寿命。

4 结果验证

为验证本文所提出分析方法的正确性，采用MASTA软件对该模型算例进行建模计算。MASTA是主流的商用传动系统分析软件，在轴承、齿轮和多轴系设计分析中广泛采用。采用表1的结构参数和图5的轴系模型，驱动力矩为800 N·m，本文提出方法与商用软件得到的计算结果如表3所示。

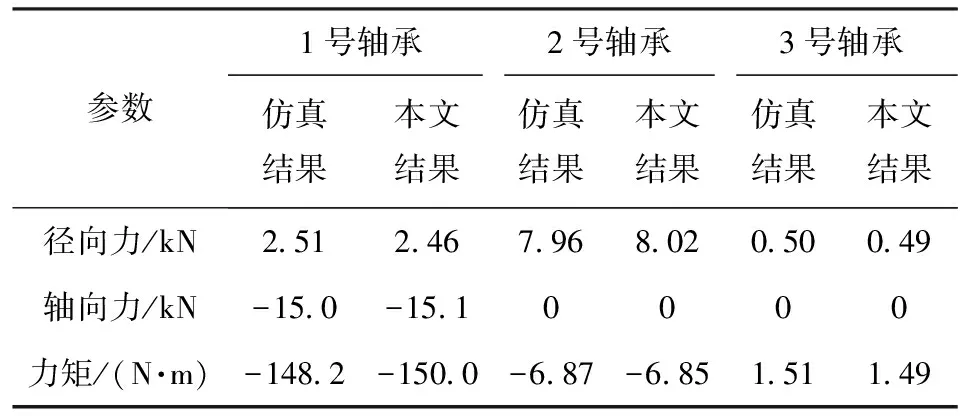
表3 计算结果对比分析Table 3 Comparative analysis of calculation results

从表3中可以看到，本文提出的方法得到的轴承径向、轴向和力矩计算结果与MASTA软件计算的结果基本一致，证明了本文方法的正确性。

为真实反映本文所研究多点支撑轴系的刚性特点，选择同型号QJ309EA、NU209EC和NU2306的轴系轴承搭建测试试验台，所搭建的试验原理图如图17所示。

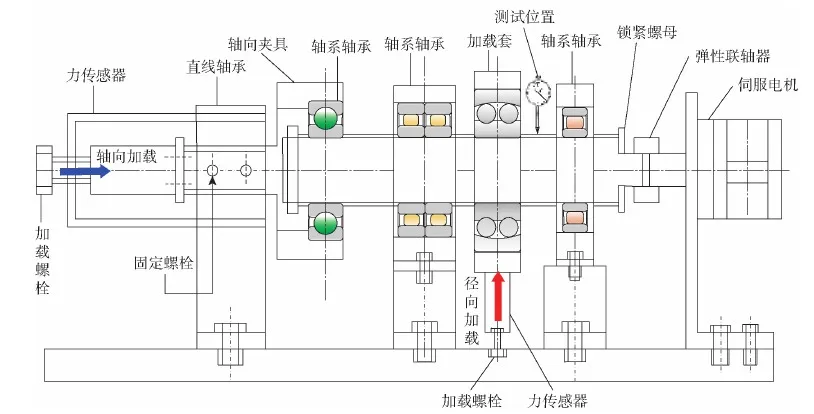
图17 多点支撑轴系刚性测试原理图Fig.17 Schematic diagram of multi-point support shafting rigidity test

QJ309EA球轴承主要承受轴向载荷，通过螺栓拉力器控制轴向载荷加载；NU209EC和NU2306主要承受径向载荷，在齿轮位置通过径向拉力器模拟载荷加载，为减小径向加载对转轴变形的影响，中间添加调心轴承，通过调心作用减少对轴角位移量影响。

将圆柱滚子轴承内圈与轴过盈配合，外圈与轴承座间隙配合，通过静态载荷加载方式测试多点支撑轴的径向位移量。由于轴系轴承采用轴承座支撑，无法直接测得其变形位移量，测试点设置在径向载荷加载点右侧中间位置(见图17)。轴承径向位移量通过千分表测试，具体操作过程如图18所示。

图18 多点支撑轴位移量测试Fig.18 Displacement test of multi-point support shafting

不同径向载荷条件下，测试支撑轴的静态位移量，为减小测量误差影响，不同加载载荷下进行5次测试，测试结果与计算结果如图19所示。

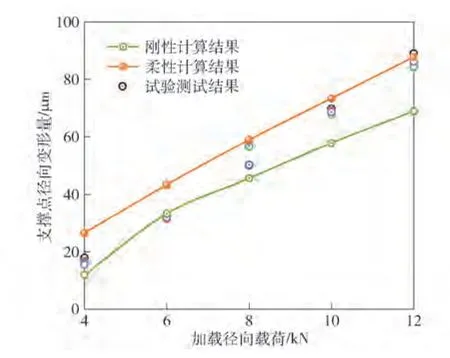
图19 多点支撑轴静态位移量结果比较Fig.19 Comparison of static displacement results of multi-point support shafting

由图19的试验测试与计算结果比较可以看出:加载载荷较小时，刚性计算结果与测试结果较接近，但随着加载载荷增加，考虑多点支撑轴变形的计算结果与测试结果逐渐趋近。其原因是在小载荷作用时，多点支撑轴系轴承的刚度对转轴的挠曲变形影响较小，随着作用载荷的增加，轴系轴承刚度的非线性变化使得转轴变形量增加，与高载荷加载的支撑轴变形量测试结果接近，从而也证明了本文所建模型的正确性。

5 结论

1)从多点支撑圆柱滚子轴承最佳凸型设计角度考虑，中间列滚子轴承选择两边弧坡修型、右端滚子轴承选择全圆弧修型，比较适合支撑轴挠曲变形对轴承接触载荷影响，有助于降低轴承的受载压力，延长轴承使用寿命。

2)从多点支撑球轴承极限爬坡率角度考虑，根据80%爬坡率安全指标要求，左端球轴承设计接触角为35°时其驱动轴最大输入力矩1 004 N·m，而在驱动力矩为正常工况800 N·m时，内沟道最大设计接触角为40.6°，外沟道最大设计接触角为44.3°。

3)从提高轴系轴承综合寿命角度考虑，齿轮作用载荷的位置的调整可以起到明显效果。L2过小或过大，轴承寿命呈明显下降趋势，在距离L2为41～46 mm范围时，轴系轴承的综合寿命L10处于最大区间。