一种折叠式共源共栅运算放大器的准确设计方法

王嘉奇，吕高崇，郭裕顺

(杭州电子科技大学 电子信息学院，浙江 杭州 310018)

运算放大器是各种模拟与混合信号系统的基本单元。它通常先根据一个顺序执行的设计流程得到初始设计，然后在电路仿真器的支持下对晶体管尺寸进行反复调整，直至满足用户要求。初始设计流程一般是基于一组解析近似方程导出的计算式[1-3]。对于现代短沟道器件电路，这样的设计方程存在较大近似误差，故所得电路性能参数将偏离指标要求，导致用户不得不在初始设计基础上进行反复调整。该过程过度依赖于设计者的经验，若经验不足，则可能耗费大量时间甚至失败。另一种方法是采用基于优化的设计技术，但是为保证精度，必须嵌入一个电路仿真器，导致计算量增加，而且最终结果在很大程度上取决于初始值的位置与优化算法的收敛性能。

文献[4]针对经典的CMOS(Complementary Metal Oxide Semicanductor)两级运算放大器提出了一种准确设计方法，仅通过少量迭代，就可使电路性能指标准确达到设计要求。与基于优化的设计方法不同，该方法弥补了传统人工设计过程中的误差，通过对该流程的迭代执行实现的。在整个设计过程中，电路的性能计算通过SPICE(Simulation Program with Integrated Circuit Emphocis)仿真，MOS管器件尺寸则通过BSIM(Berkeley Short-channel IGFET Model)等精确模型确定，因此可消除人工设计方法中存在的误差。本文将这种方法用于折叠式运放的设计，取得了良好的效果。

1 传统设计方法

常用的折叠式运算放大器电路结构如图1所示。

图1 折叠式共源共栅运算放大器电路结构图Figure 1. Schematic of folded cascode operational amplifier

根据对小信号等效电路的分析，其主要性能指标可表达为以下计算式[5-6]。

增益(Av)为

(1)

相位裕度(Phase Margin，PM)为

(2)

其中，pnd为次极点

(3)

Ce=Cdtot1+Cdtot5+Csb7

(4)

单位增益带宽(Unity Gain Bandwidth，UGB)为

ωu=gm1/CL

(5)

大信号压摆率(Slew Rate，SR)如式(6)所示。

SR=Ids3/CL

(6)

根据上述性能指标，传统人工设计流程如表1[5-6]所示。式(1)～式(6)及表中各符号的意义与文献中相同。此设计方法依次计算每个晶体管尺寸的过程，其主要依据是UGB、SR指标、输入共模信号范围与输出摆幅。

Vinc，max=VDD-Vov4+VTn

(7)

Vinc，min=Vgs1+Vov3+VSS

(8)

Vout，max=VDD-Vov5-Vov7

(9)

Vout，min=Vov9+Vov11+VSS

(10)

第1步由摆率确定偏置电流；第2步由UGB决定的gm1与电流确定M1，2管的长宽比；第3～5步由M5～M11管的过驱动电压确定各自的长宽比，其中假定M4，5与M6，7，M8，9与M10，11的过驱动电压相同。最大输入共模信号与输出摆幅都与M4，5的过驱动电压有关，因此应取其较小值[7]。

表1 折叠式共源共栅运算放大器设计流程

对于现代短沟道器件电路，这一设计过程产生的误差主要来自两个方面：(1)确定长宽比时采用平方律MOS模型产生的误差；(2)各性能指标表达式，例如式(5)、式(6)由简化等效电路得出，忽略了各种寄生元件，因此会产生误差。

为消除设计流程中的误差，在确定长宽时必须采用精确的MOS模型，例如使用BSIM3/4、PSP或EKV[8]。设基于这些模型的Ids电流方程是

Ids=f(W，L，Vgs，Vds，Vbs)

(11)

准确宽度W的计算应通过f的反函数来计算

W=f-1(Ids，L，Vgs，Vds，Vbs)

(12)

这可通过数值方法来实现，例如构建数值反函数模型，或通过牛顿迭代法求解非线性方程

(13)

式中，Ids(W)是由f表示的电流。

其次，必须通过电路仿真计算获得电路性能指标。准确的电路性能一般与电路所有参数有关，例如对该电路，准确的UGB、SR可表达为

ωu=ωu(gm1，CL，…)

(14)

SR=SR(Ids3，CL，…)

(15)

其中，省略号表示电路中其余参数。

但采用这样的计算后，将无法再如表1中的设计流程逐个计算MOS管尺寸。式(11)中的电压Vds和Vbs在设计完成前是未知的；如式(14)、式(15)所示的UGB、SR等指标的精确表达式与电路中所有参数有关，因此无法单独通过gm1和Ids3确定M1的尺寸。

2 精确设计方法

设计时要将所有误差因素均考虑在内，性能指标与设计参数之间的关系将是一个复杂的非线性方程组。表1的设计流程实际是采取了一些近似操作，在忽略了MOS模型与性能指标计算时的高阶效应后，使这个方程成为顺序可解。但采用了精确MOS管模型与性能计算方法并考虑忽略的误差后，不同设计参数之间便相互耦合，使表1各步骤尺寸参数的顺序计算(即方程的顺序求解)变得不可能[9]。为了在考虑误差的同时又避免复杂非线性方程的求解，文献[4]针对常见的两级运放，提出了一种既能弥补传统设计方程中的误差，又能利用解方程的松弛迭代对设计流程反复执行以消除误差的方法。其基本思想是先根据传统设计获得一个初始电路，然后将存在的误差弥补到传统设计流程的相关方程中，并重复执行；同时采用基于BSIM等模型的器件尺寸计算，收敛后即可得到性能指标准确符合要求的电路。

下面介绍将该流程用于折叠式运放设计的具体做法。首先对弥补表1设计流程中性能指标误差的方法进行说明。电路性能参数的精确表达虽然与所有电路参数有关，但其主要部分仍是传统设计时采用的近似式。例如对UGB和SR，其精确值可分别表示为

(16)

SR=Ids3/CL+ΔSR

(17)

Δωu与ΔSR是精确值与解析近似表达之间的误差。在设计过程中，这个误差可从上一次迭代的电路中估算出来

(18)

(19)

(20)

(21)

将得到的新gm1和Ids3代入原设计流程，就可对上一次得到的设计参数进行修正。

对于计算器件尺寸时采用简单平方律模型带来的误差，必须采用BSIM等精确模型。但采用式(12)的精确模型后，宽度计算中需要Vds和Vbs的值，这在设计该器件时是未知的。对于工作在饱和区的MOS管而言，Ids主要由Vgs决定，Vds、Vbs的影响不大，因此在长度给定的情况下，若已知Vds、Vbs的一个近似估计，则宽度仍可根据器件本身的Ids与Vgs决定

(22)

式中，Vds0、Vbs0分别是Vds、Vbs的近似值，可从上一次迭代的电路中得到。因此在设置好各器件的长度后，表1设计流程中长宽比的计算(除M1)均可用式(22)替代[10]。

表1中M1的尺寸是根据其偏置电流与跨导gm决定的。采用基于BSIM的方法后，为保证精度，需根据如下两变量方程

(23)

同时解出宽度与Vgs。

综上所述，可以得到一个迭代设计算法：首先，根据表1的传统设计流程得到电路初始设计；然后，通过SPICE仿真获得电路第k次迭代时的性能参数及各MOS管的Vds、Vbs，并用式(20)～式(23)替换表1中相应步骤的表达式，可得第k+1次的设计结果。重复此过程直至收敛；最后，可得到准确满足性能指标要求的电路。这一迭代设计算法的流程图如图2。

图2 设计算法流程图Figure 2. Flow chart of the designed algorithm

图中，P代表电路性能参数矢量，计算式为

P=[AvωuφmSR]

(24)

图中最后一个方框的具体步骤如表2所示。

表2 折叠式共源共栅运算放大器设计流程

其中各步基本与表1对应。设计时先确定所有MOS管的长度，然后按传统方法进行初试设计。对短沟道器件，为减小误差，初始设计确定尺寸时建议采用gm/Id方法[11-12]，然后再按图2流程进行迭代。

需要指出，表1传统设计过程中没有涉及到增益和相位裕度，这样得到的电路增益将主要由选定的器件长度决定，但无法准确控制。相位裕度按式(2)将取决于M7源极的寄生电容，也无法控制。图2设计流程考虑了这两个指标，方法与UGB、SR的设计式式(16)～式(21)类似。首先对增益和相位裕度的表达式(1)、式(2)进行误差补偿

(25)

(26)

式中

(27)

(28)

根据这两个增量，通过改变相关器件的长度和pnd来进行增益和相位裕量的设计[13-15]。对于增益，将误差表达式(27)代入式(25)，可得

(29)

式(29)为gds9、gds11积的更新值(这里选择这两个电导，也可选gds5，7)。分别将它们取为

(30)

由于gds主要取决于器件长度，因此可通过改变长度来改变gds。为保证精度，根据基于BSIM模型的输出电导表达式来计算这两个管子的长度。输出电导为

(31)

长度为

(32)

具体也可用式(13)求宽度的方法。对相位裕量设计时，将误差表达式(28)代入式(26)，可得

(33)

由此可对次极点进行修正。通过改变M7的栅长来修正这一次极点[16]。利用Cgs=(2/3)WLCox，将式(4)表示为

(34)

其中

(35)

由式(33)确定的pnd修正值得出M7的新栅长，如式(36)所示。

(36)

3 设计实例

下面给出采用该方法的设计示例。本文采用0.18 μm工艺和90 nm工艺，运算放大器的电源电压分别为VDD=1.8 V和VDD=1.2 V，负载电容均为CL=1 pF，VSS=0 V。两种工艺下要求的性能参数指标与设计结果如表3和表4所示，设计的晶体管尺寸如表5和表6所示。

表3 放大器的性能指标(0.18 μm工艺)

表4 放大器的性能指标(90 nm工艺)

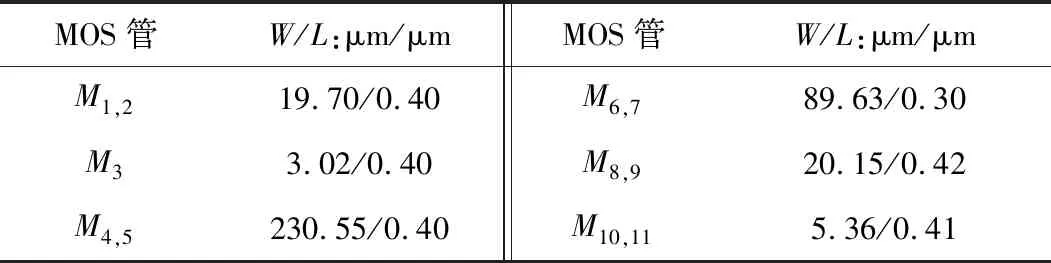
表5 设计MOS管尺寸(0.18 μm工艺)

表6 设计MOS管尺寸(90 nm工艺)

设计过程中，MOS管采用工艺库提供的BSIM3v3模型，电路仿真采用HSPICE，在MATLAB中实现迭代过程。从表3及表4可以看出，设计所得电路性能参数与要求指标准确吻合。图3为迭代过程中Av、UGB、PM、SR的变化，可以看出迭代开始时这些指标显著偏离目标值，但分别经过13次和11次迭代后，均收敛于要求的指标。

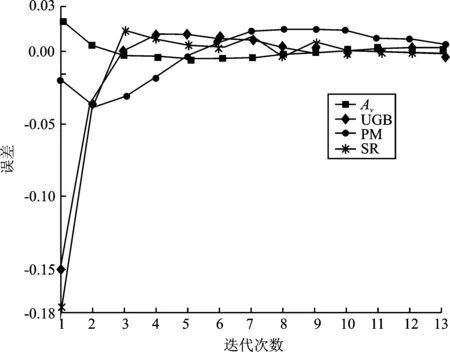
(a)

(b)图3 松弛迭代过程 (a)0.18 μm工艺 (b)90 nm工艺Figure 3. Iterative design process (a)0.18 μm process (b)90 nm process

最后还要说明，用表2计算M3～M11时，Vgs取Vov+VTn，p，过驱动电压仍按表1中相同方法确定。对于短沟道器件，由于过驱动电压与饱和电压Vds，sat之间存在一定差异，这将使电路输入输出电压范围产生一定误差[17]。对本例的0.18 μm工艺及90 nm工艺，这种误差不大。对于更短沟道工艺，可将输入输出电压范围作为性能指标，与上述Av、UGB等指标一样，加入到迭代过程中进行修正，收敛后得到与预定指标完全吻合的值。

4 结束语

使用本文迭代算法设计出的运算放大器能精确满足性能参数的期望值。这种方法消除了传统设计流程中由于简化的MOS模型和性能指标表达近似所产生的误差，为这一广泛应用的电路提供了有效的设计方法。相较常用优化方法需要的成百上千次仿真，本文方法每次迭代只需一次SPICE仿真，因此具有计算量小、设计精度高的优点。在后续的版图设计中，由于寄生效应电路性能还可能产生误差，因此今后的研究重点也将为尽可能消除误差带来的影响。