一种复杂噪声环境下的机电系统故障在线监测声学处理方法

白兴宇，苟宇涛，姜 煜，刘明禹

(杭州电子科技大学 电子信息学院，浙江 杭州 310018)

随着科学技术的进步，机械设备不断向大型化、高速化、连续化、集中化和自动化的方向发展，其组成和结构也日益复杂，不同设备之间的联系也越来越密切，一旦设备的某个部分在运行过程中出现故障，且故障发展并积累到一定程度时，就会引发机械系统重大事故，因此越早发现故障，越有助于机械设备安全可靠运行。但是由于机械设备早期故障特征较弱，以及实际运行过程中复杂背景噪声叠加，使得提取和识别早期故障信号变得十分困难[1]。因此，先进的微弱信号检测技术和背景噪声抑制技术对于提高识别机械设备故障的准确性具有十分重要的作用。

随着信号处理、人工智能、模式识别等技术的发展，各种新的融合方法也不断地被引入到机电故障监测中。文献[2]对背景噪声的系统进行去噪处理，结合小波去噪提出改进的阈值去噪方法。文献[3]对谱减法语音增强算法进行了改进，重点对声纹识别特征参数进行了提取，详细分析了高斯混合模型参数估计。常见的机电故障检测方法包括经验模态分解[4-6]、独立分量分析[7-9]、小波分析[10-14]等。文献[15]将峰值检测专利技术在实际的滚动轴承故障诊断中进行了应用，证明了峰值检测技术在轴承故障诊断中的突出作用。文献[16]通过对峰值检测技术的应用，发现机器小幅不平稳运转不会对诊断结果产生影响，效果较为突出。在实际复杂的操作环境中，机电各个部件以及背景噪声的影响使得采集真正有用的信号非常困难，这也导致机电早期故障不易被发现[17-18]。

针对复杂背景噪声环境下的机电系统故障检测问题，本文提出了一种基于声学处理的噪声抑制和故障监测方法。该方法首先通过声学传感器拾取机电系统运行过程的声纹信号，再通过背景噪声抑制技术去除机电系统运行过程中背景噪声，结合峰值检测技术，同时通过测量信号间动态时间弯曲距离对信号分类判型，最终实现对复杂噪声下的机电系统故障的在线监测和识别。该算法将基于动态时间弯曲算法的声纹信息匹配技术与峰值检测技术以及基于数据跟踪的自相关处理技术进行有机结合，有效解决了复杂噪声环境下的机电系统故障检测问题。为验证该算法的有效性，本文采用数值仿真分析了该算法在低信噪比情况下的噪声抑制能力、峰值检测的应用效果以及故障信号判型效果。

1 复杂噪声环境下机电系统故障在线监测声学处理方法原理

传统故障检测方法仅能发现和判断已经发生且较为严重的典型机电设备故障，其对一些隐性故障的预判能力相对不足，难以辨别复杂噪声环境下的故障信号特征频率及其倍频。基于此，本文利用具有良好信息拾取能力的声学传感器，结合自相关噪声抑制技术、峰值检测技术以及声纹信号匹配比对技术，通过对机电系统运行状态下产生的声纹信号采集、跟踪和背景噪声抑制，实现了对机电设备故障的在线监测。本文设计的一种复杂噪声环境下的机电系统故障在线监测声学处理方法总体原理框图如图1所示。

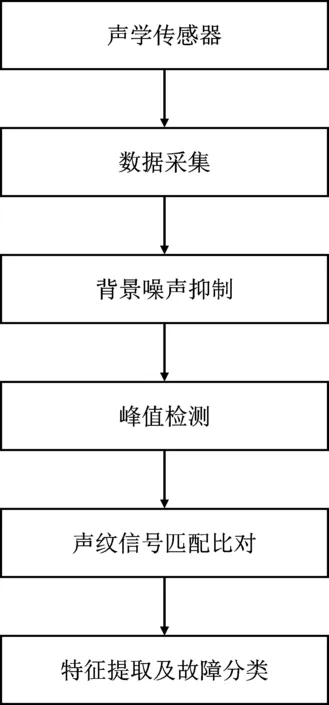
图1 复杂噪声环境下的机电系统故障声学处理方法总体原理框图Figure 1. Schematic diagram of acoustic treatment method for mechanical and electrical system faults incomplex noise environment

1.1 复杂背景干扰噪声抑制

在工程实践中，机电设备运行状态的信号包含有用的特征信号与背景干扰噪声信号。在故障早期，真正的有效信号较为微弱，容易淹没在复杂的强背景干扰噪声中。为了能较好地提取到有用的声学信号，首先需要对背景干扰噪声进行抑制，使提取到的机电设备运行状态声学信号能够最大程度地表征机电设备运行状态的特征信息。自相关滤波技术进行噪声抑制效果较好，该方法可在输入信号与噪声的统计特性未知或变化的情况下，自动估计出所需的统计特性，并以此为依据自动调整参数，以达到最佳的降噪效果。

自相关函数描述的是同一信号在不同时刻的相互依赖关系，其定义如式(1)所示。

(1)

在实际生活中背景噪声多种多样，主要包括带通噪声、冲击噪声和白噪声。白噪声在现实中十分常见，其既是时域上的随机信号也是频域上的随机信号。标准的白噪声应该是方差恒定不变的数值，均值为0，即E[x(n)]=0，E[x(n)2]=б2。

机电系统正常运行过程产生的目标信号具有较强的相关性，复杂的背景噪声相关性较弱，而自相关处理方法实际上是根据信号的相关详细程度滤除信号里不相关的部分，因此自相关处理技术可滤除机电系统正常运行状态下的背景噪声信号，适用于机电系统运行过程的背景噪声抑制。正弦信号或者其他确定性信号在所有的时间位移上都有自相关函数，本文采取特定频率的正弦信号和白噪声信号来模拟实际运行过程中的正常信号和噪声信号。运用自相关处理技术降噪后，噪声信号的自相关函数随τ的增大趋于零，使得信噪比提升，故此方法具有显著的降噪效果。

1.2 机电系统运行状态声纹信号的峰值检测

峰值检测技术作为一项由国外发展而来的振动信号分析技术，是一种在某时间间隔内对信号时域波形峰值进行捕捉的信号处理与检测方法。当机电系统中的金属发生相互碰撞时，会产生一种应力波，而峰值检测则可以采集和检测这些短暂出现的应力波，通过对其峰值以及出现频率的提取，转换成频谱进行故障分析。基于峰值检测技术的机电故障检测实现原理如图2所示。

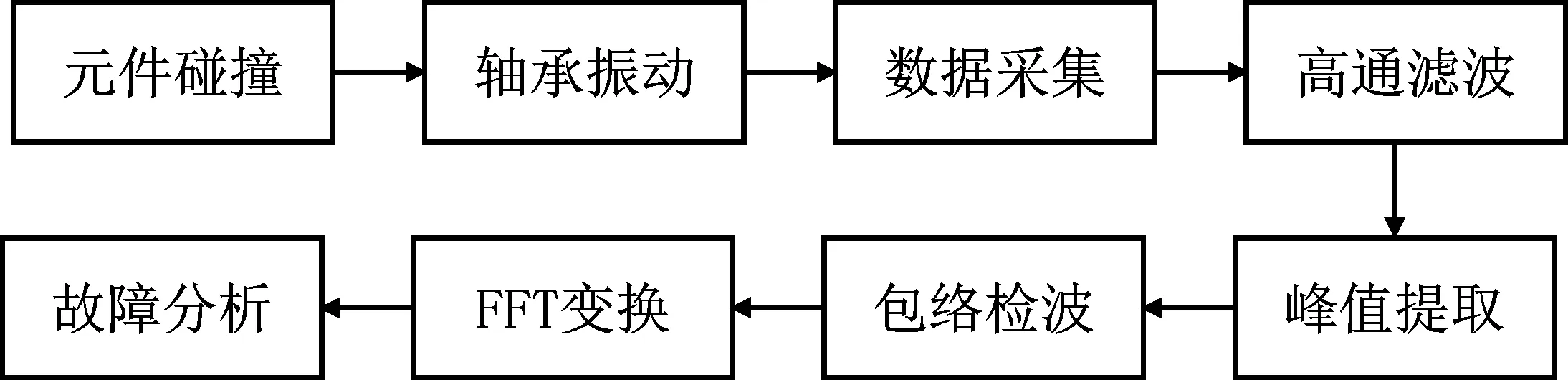
图2 基于峰值检测技术的故障诊断原理图Figure 2. The fault diagnosis schematic diagram based on PeakVue technology

由图2可以看出通过传感器采集及高通滤波器进行滤波后，方可得到峰值检测方法分析的目标信号。高通滤波器主要是为了使信号集中于冲击信号所在频段、分离冲击信号和普通振动信号，此分析方法的核心就在于峰值。一般情况下，频率带宽决定所选时间间隔，峰值就在原始振动信号中选定某一时间间隔中出现。峰值检测技术就是通过提取某时间间隔的峰值，再进行包络检波以及傅里叶变换，最终实现对振动信号的故障分析。

由于工作过程中实际操作以及环境的复杂性，峰值检测技术的实际应用情况并不理想，复杂环境下包含太多的噪声，使得目标信息很难在众多的峰值中被分辨出来。在过多干扰噪声的影响下，无法有效应用峰值检测技术。因此，本文将峰值检测技术与复杂噪声下背景干扰噪声抑制技术相结合，当在实际的复杂背景下工作时，先用背景噪声抑制技术滤除大量复杂噪声，再用峰值检测技术提取目标信号的峰值，这一过程使得噪声信号被更大程度滤除，可提取到更有利用价值及参考性的峰值。综上所述，复杂噪声环境下的机电系统故障声学处理方法具体原理流程图如图3所示。

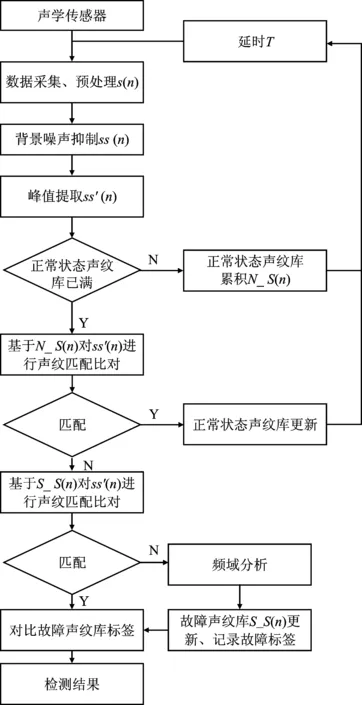
图3 复杂噪声环境下的机电系统故障声学处理方法原理流程图Figure 3. Schematic diagram of acoustic treatment method for mechanical and electrical system faults in complex noise environment

由图3可以看出该方法主要基于声学信号拾取和处理，通过背景噪声抑制和峰值检测后建立正常状态声纹库和故障状态声纹库，再通过声纹匹配对比技术实现对信号的分类判型，进而实现对机电系统运行状态和隐形故障的有效监测和判型。此算法可以有效地解决降噪后的信号处理问题及峰值检测技术在复杂背景噪声环境下的实际适用问题，在复杂噪声情况下也能检测出机电早期故障，并且能够准确预测出严重程度，提高了信号的利用率。

2 复杂噪声环境下机电系统故障在线监测声学处理方法实现

2.1 峰值检测技术的应用

峰值检测技术主要基于希尔伯特变换法来实现。希尔伯特变换对分析信号的瞬时幅度和频率和对信号包络的快速提取有较好的效果，因此本文采用希尔伯特变换实现峰值检测。根据希尔伯特的物理意义可知，当包络信号经过希尔伯特变换后，其峰值刚好与变换后的信号正向过零点相对应，因此可将包络信号峰值检测转换为正向过零点检测，包络信号的峰值改变并不会影响信号正向过零点检测，并且不需要设置任何幅度阈值。实信号x(t)的希尔伯特变换的定义为

(2)

式中，“*”表示卷积运算符。根据上式可知，信号x(t)的希尔伯特变换实际上是信号的卷积。希尔伯特变换的频率定义为如下

(3)

式中，x(f)是信号x(t)的傅里叶变换；j是虚数单位。由上述两式可知，信号x(t)的希尔伯特变换为

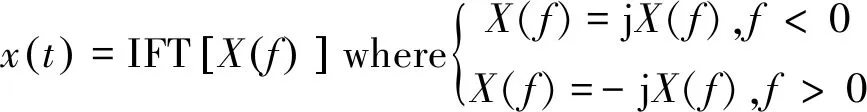
(4)

式中，IFT表示傅里叶逆变换。结合上式可发现，对于实信号的峰值检测可以借助希尔伯特变换运用傅里叶变换进行快速计算。

在此思想上，本文运用希尔伯特变换实现峰值检测技术在识别故障信号上的应用，建立正常状态声纹库，为声纹信号的匹配识别准备条件。

2.2 机电设备运行状态声纹信号的匹配比对

本文中声纹信号匹配技术以动态时间弯曲算法为基础。动态时间弯曲算法基于动态规划思想，是一种计算时间序列数据之间相似度的算法。该算法可以通过对时间序列时间点的弯曲，使得两条时间序列中的波峰、波谷准确匹配。动态时间弯曲算法还具备很多欧氏距离不存在的优势，其可以对长度不等的时间序列进行距离度量。动态时间弯曲不需要满足三角不等式约束条件，可以根据时间序列数据特点进行异步匹配，且其对于时间序列数据的异常点和噪声等缺点有良好的适应性。

机电设备声纹信号的监测识别是通过比较机电设备当前运行状态与过去运行状态之间的差异来实现的。基于此，对声学传感器采集到的正常声学信号进行宽带背景干扰噪声抑制和峰值检测，并建立正常状态声纹库。以此作为参考，采用动态时间弯曲算法分别测量目标检测声纹信号和正常声纹信号与正常状态声纹库的匹配距离，并对其相似度进行比较，实现对检测信号的分类识别。本文设计的匹配比对算法原理框图如图4所示。

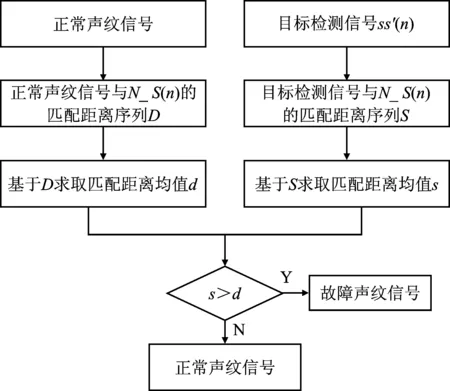
图4 机电设备运行状态声纹信号的匹配比对原理图Figure 4. Schematic diagram of voiceprint signal matching and comparison in operation state of electromechanical equipment

由图4可以看出，该算法可通过计算正常声纹信号与正常状态声纹库的匹配距离序列D和目标检测信号与正常状态声纹库的匹配距离序列S，从而求得匹配距离均值d和s。若s>d，则说明两个信号相似度低，则将目标检测信号判定为故障信号；若s≤d，则说明两个信号相似度高，则判定为正常信号。

3 数值仿真

机电系统设备运行一旦出现故障，便伴随着巨大的经济损失与灾难，且事故一旦发生，便没有分析其信号的必要，故实际操作中可被采集到的故障样本数据较少。为了验证算法性能，本文利用MATLAB进行了仿真。机电设备运行状态声纹信号的数学模型可用多个频率、幅值不同的正弦波复合而成。仿真中用正弦波信号模拟机电系统正常运行状态下的声纹信号，模拟复杂干扰为高斯白噪声及一些正弦信号。本文设置采样频率为4 096 Hz，采样点数为2 048，为验证自相关处理方法在不同噪声环境下的降噪效果，本文设置不同的信噪比环境进行对比，并使用该方法对不同的含噪信号进行降噪处理。所获得的仿真结果如图5～图7所示。

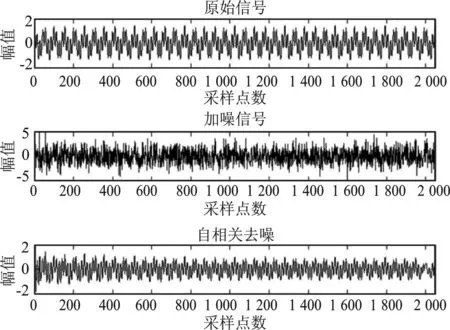
图5 含噪信号1降噪时域波形图Figure 5. Noise signal 1 denoising time domain waveform

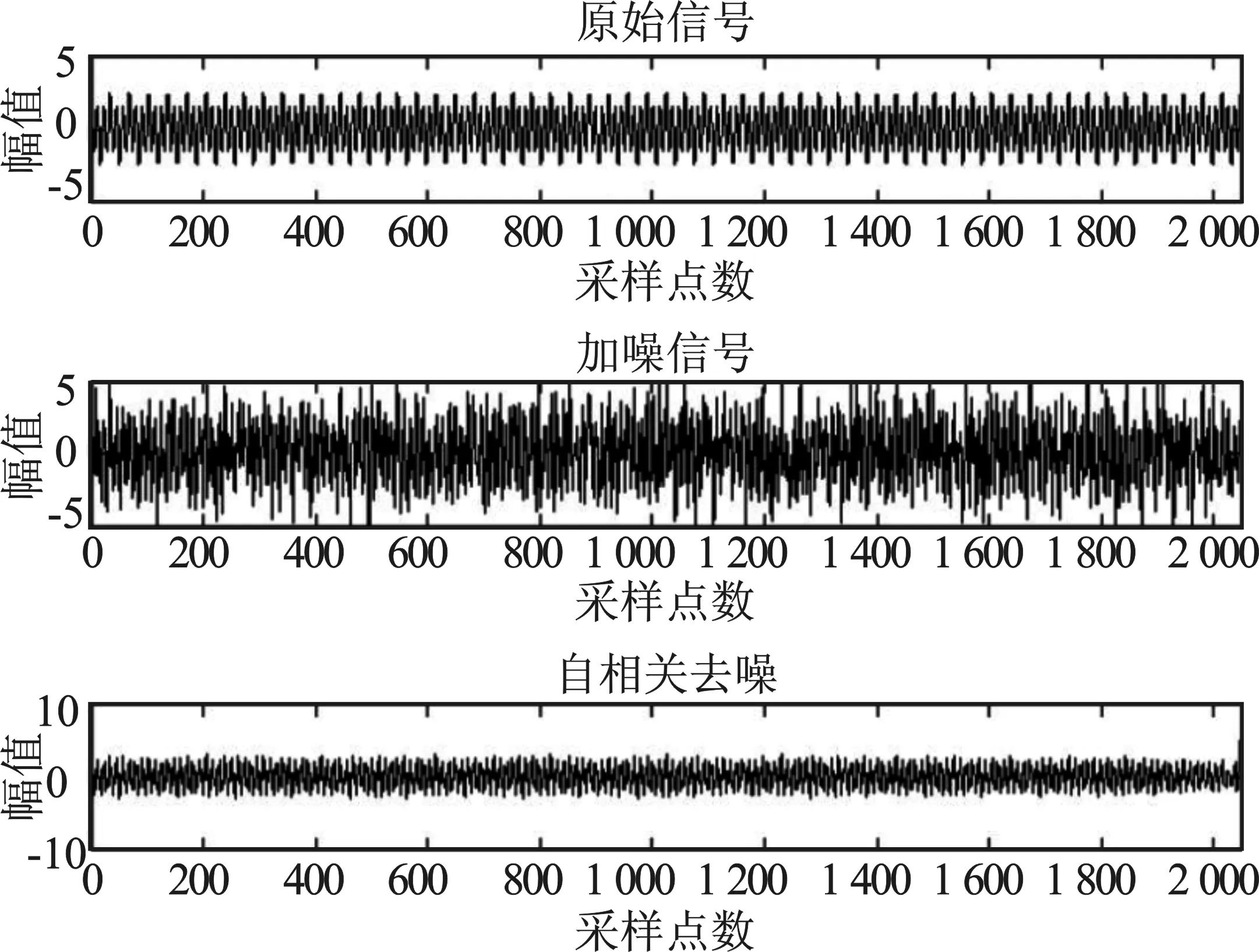
图6 含噪信号2降噪时域波形图Figure 6. Noise signal 2 denoising time domain waveform

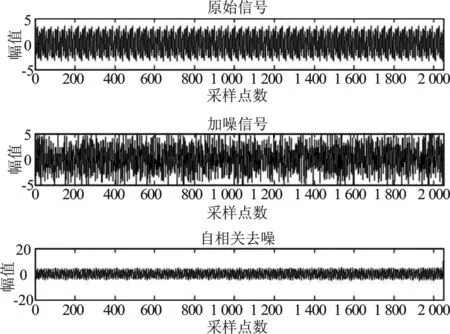
图7 含噪信号3降噪时域波形图Figure 7. Noise signal 3 denoising time domain waveform

由图5～图7可以看出信号经自相关去噪方法之后，干扰噪声可被有效抑制，处理后的信号时域波形特征更为简洁清晰。降噪前信号的信噪比分别为0.802 6 dB、-2.230 2 dB、2.673 1 dB，降噪后声纹信号的信噪比分别为8.1 806 dB、3.664 2 dB、6.323 3 dB，由此可以看出针对不同的噪声环境，该方法抑制干扰噪声均有良好的作用效果。综上分析，该方法对复杂噪声情况下的抑制效果较为明显，证明本方法对干扰噪声的抑制效果较好且抗干扰能力较强，具有良好的可靠性。

对于机电设备运行状态的检测，本文结合峰值检测技术对信号进行提取。在实际情况下高通滤波器截止频率选择1 000 Hz或2 000 Hz。为便于观察，本次仿真假设高通滤波器截止频率设为1 000 Hz，频带宽度设为10 Hz，采样时间间隔即为39 ms，并用正弦信号模拟高通滤波器分离出的高频信号和应力波信号。本文给出了含噪信号1及其降噪后的峰值检测时域波形图，仿真图如图8和图9所示。

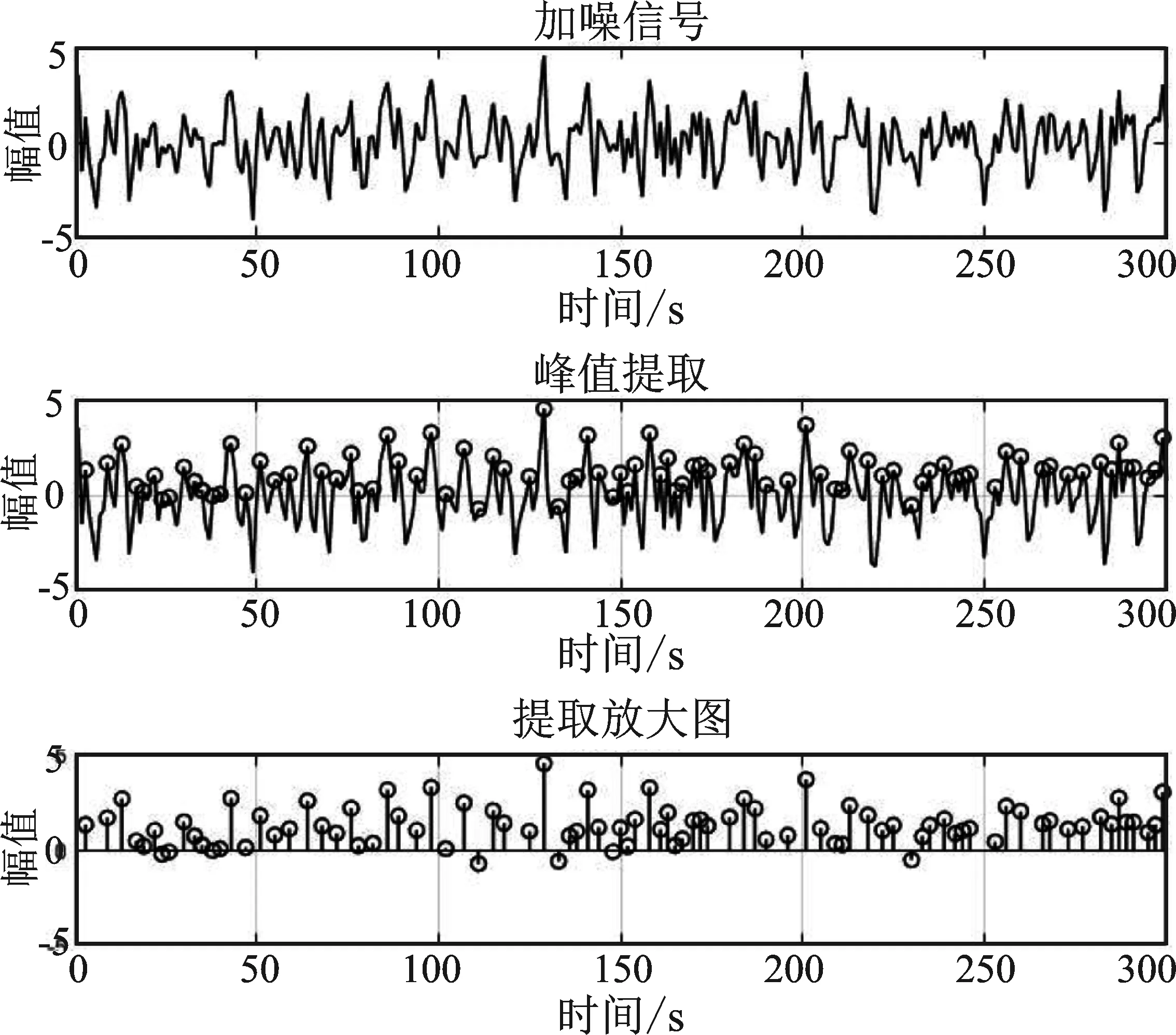
图8 含噪信号1峰值检测时域波形图Figure 8. Peak detection time domain waveform of noise signal 1

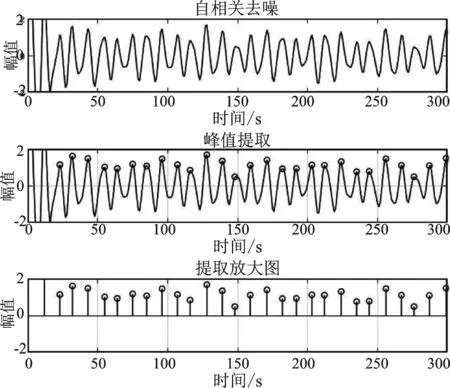
图9 含噪信号1降噪后峰值检测时域波形图Figure 9. Noise signal 1 time domain waveform of peak detection after denoising

通过图8和图9的仿真图可以看出峰值检测仍能精准提取幅值频率较低的峰值，说明峰值检测技术对于一些微弱的峰值信号灵敏度较高，因此可结合背景噪声抑制技术精准提取早期故障信号，具有实践意义。

对于机电设备运行状态声纹信号的匹配识别，本文采用动态时间弯曲距离来度量样本之间的相似性。通过比较声纹信号的动态时间弯曲距离均值来区分正常信号与故障信号。本次仿真将模拟声纹信号平均分为了30等份，每份信号的长度为400，每种声纹信号模拟了30个样本，其中，“*”型曲线表示正常声纹信号与参考信号之间的动态时间弯曲距离，菱形曲线表示故障声纹信号1与参考信号之间的动态时间弯曲距离，“×”型曲线表示故障声纹信号2与参考信号之间的动态时间弯曲距离，仿真结果如图10所示。

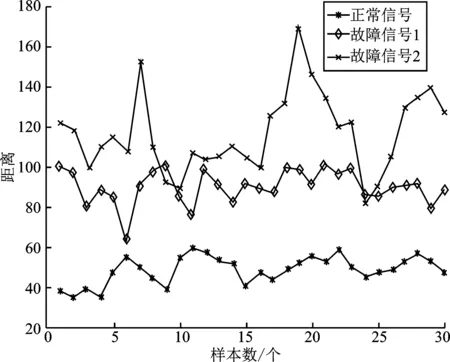
图10 机电设备运行状态不同声纹信号动态时间弯度距离Figure 10. Dynamic time curvature distance of different voice print signals of mechanical and electrical equipment in operation state

动态时间弯曲距离是对时间序列数据进行处理，故对其无单位要求。由图10可以看出，经测得正常声纹信号的动态时间弯曲均值为51.788，故障声纹信号1的动态时间弯曲均值为91.552，故障声纹信号2的动态时间弯曲均值为119.318。由不同信号间的均值差异可以看出，依据动态时间弯曲计算匹配距离并比较均值的方法可将正常声纹信号与故障声纹信号明显区分开，并且对不同故障声纹信号的区分效果也较为明显。

均方根值、绝对值平均值表征信号的能量，可反映出信号的有效值。为了进一步说明本文整体算法处理信号的性能，本文在不同信噪比环境下，采用上文所提的降噪、峰值检测以及信号匹配等方法对过程处理前后的信号绝对值平均值、均方根值进行比较。在保证相同的背景环境下，处理前后信号对比曲线如图11和图12所示。

通过图11和图12的仿真图可以看出，处理前后信号绝对值平均值、均方根值都随着信噪比增加而降低且处理后信号值较低，说明处理后信号对有效信号的提取率更高。处理前信号在SNR=-13 dB环境下的绝对值平均值、均方根值分别为4.896 2、6.168 5，处理后数值为1.864 6、2.873 4；在SNR=-8 dB环境下处理前绝对值平均值、均方根值分别为2.910 7、3.634 7，处理后为1.222 8、1.550 1，说明在不同的信噪比环境下，该算法都具备较好的信号处理能力，即使在低信噪比下即复杂噪声环境的情况下，该方法的处理效果也比较明显。

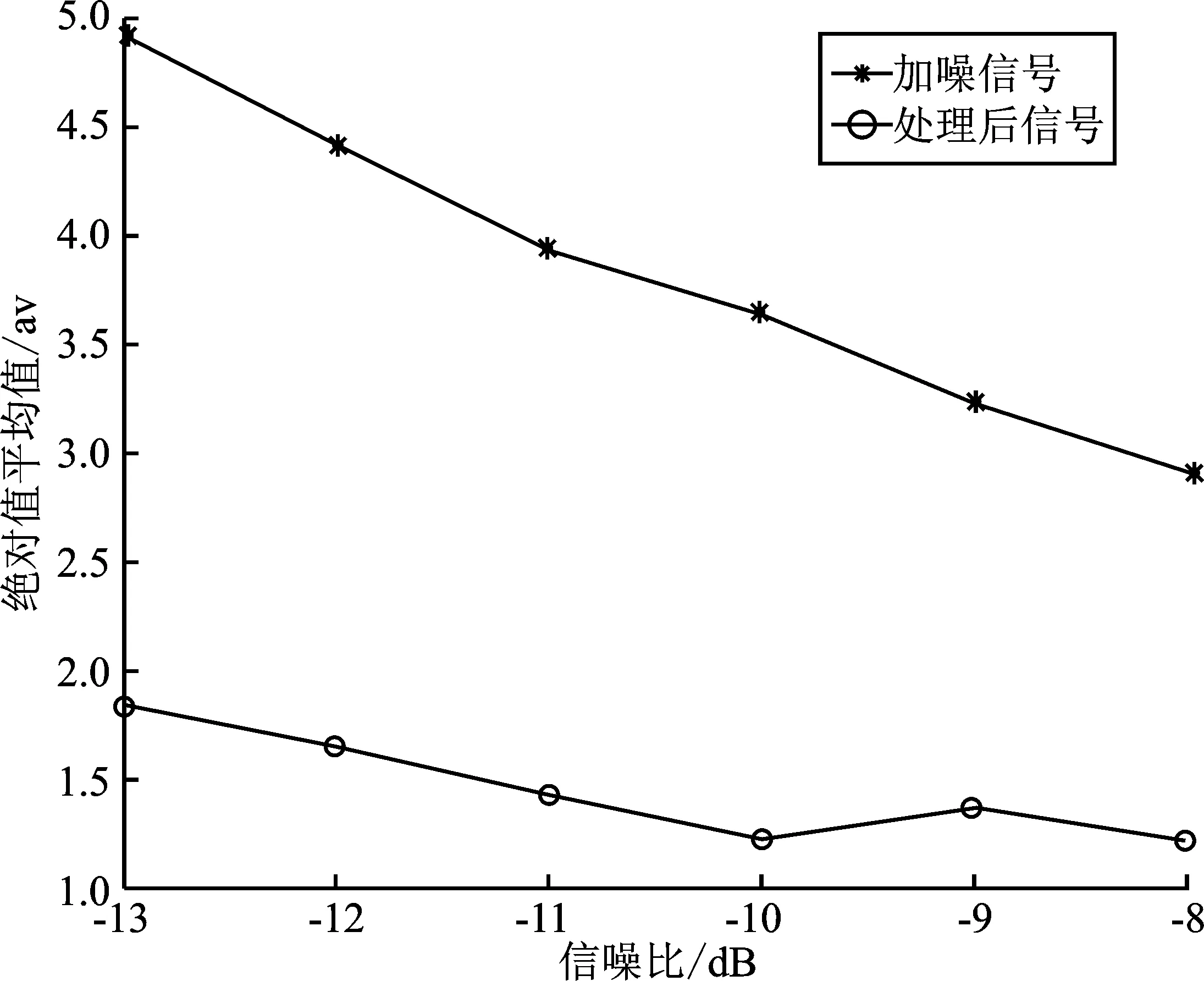
图11 处理前后信号绝对值平均值对比Figure 11. Comparison of the mean absolute value of signal before and after processing

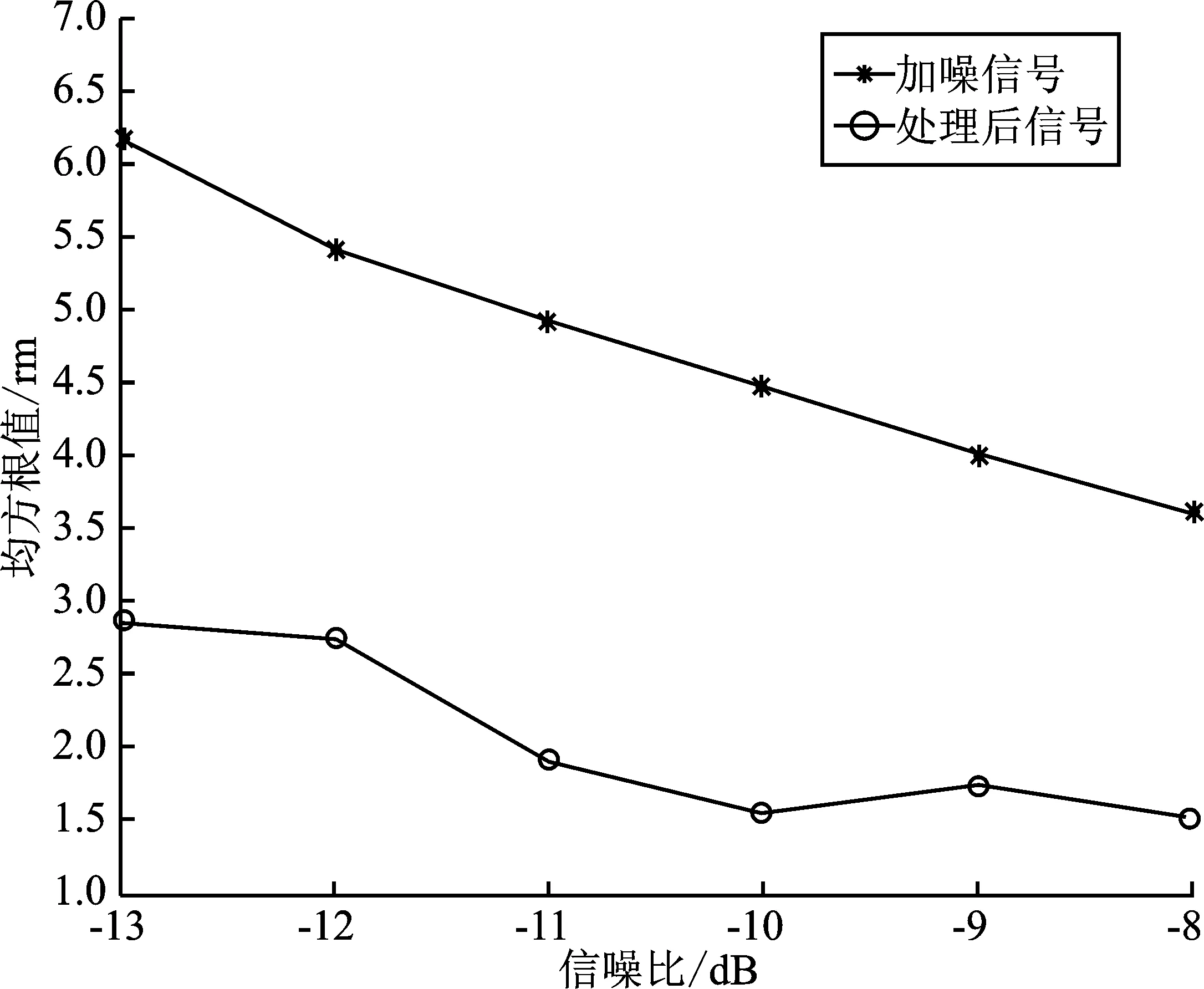
图12 处理前后信号均方根值对比Figure 12. Comparison of root mean square values before and after processing

综合仿真结果及分析，表明本文所提复杂噪声环境下机电系统故障监测的声学处理方法有较好的抗干扰能力，在信噪比低的环境下对有效信号的提取和检测效果性能良好，具有较好的可靠性，适用于复杂噪声环境下对信号的处理。

4 结束语

本文针对传统故障分析的局限性，提出了一种复杂噪声环境下机电系统故障在线监测的声学处理方法。该方法基于声学信号拾取和处理，通过对机电设备正常运行状态下的声学信号进行拾取、数据跟踪、基于自相关处理的背景噪声抑制和峰值检测技术建立声纹库；然后通过声纹信号的匹配比对技术，实现故障信号的识别和分类，进而实现在复杂背景噪声环境下对机电系统故障的在线监测和有效判型。通过仿真实验证明，该方法有较强的抗干扰能力，可提高信号的利用率，有效降低误检率，使得检测结果更加准确。