采用改进人工势场法的动态无人车路径规划

邱朋，汪光，赵理，赵博阳

（1.北京信息科技大学机电工程学院，北京 100192；2.河北工业大学人工智能与数据科学学院，天津 300401）

1 前言

随着智能驾驶技术的发展，无人驾驶车辆越来越多的运用到人们的生产生活中，其相关技术可分为：定位导航、环境感知、路径规划以及自动控制技术，其中无人驾驶车辆路径规划与行驶避障一直是研究的重点[1]。路径规划是指在已知或未知的环境中，由车载雷达、视觉传感器等获取外界信息后，利用车载控制器规划出一条由起点到目标点的无碰撞轨迹。由于实际车辆行驶过程中更多时候处于动态环境，目前针对路径规划相关算法各国学者研究广泛，但对于动态避障问题仍有待进一步研究[2−4]。

人工势场法是路径规划算法中一种常用的方法，该算法原理简单易理解，是一种准确性与实时性较高的一种方法[5]，因此被广泛应用于无人车以及机器人等领域的路径规划求解当中，但对于动态环境的适应性较低，无法满足无人车处于动态环境中所需路径准确稳定的要求。文献[6]在动态路径规划过程中，考虑了速度因素的影响，解决了路径抖动不稳定的问题，但未考虑行驶道路边界的限制，在实际行驶中可能驶出道路。文献[7]中提出一种斥力偏转模型，修正斥力方向，降低了规划路径的长度及曲度，但并未对考虑实际行驶环境中的速度因素，因而无法准确描述实际行驶场景。文献[8]中提出一种高斯人工势场算法，该算法针对结构化道路环境，增加车道中心线对行驶车辆的引力，增加了汽车避障过程的稳定性，但当汽车离车辆中心线较远时，该方法会面临路径抖动的问题。

因此，结合实际汽车行驶环境及车辆外形特征，借鉴人工势场法的基本思想，改进斥力势场函数，应用椭圆化距离代替斥力势场的中的实际距离，构造道路边界势场、障碍物速度势场，引力势场多重约束下的改进人工势场模型。同时，基于纯追踪算法理论，建立以转角为控制变量的路径跟踪模型，并通过Matlab验证改进算法的路径规划及跟踪效果。

2 传统人工势场法

人工势场法应用与无人车路径规划的基本思想是将无人车在周围环境中的运动虚拟为在受力场中的运动，障碍物对无人车产生斥力，目标点对无人车产生引力，无人车受引力与斥力的共同作用下，由起点沿着势场强度下降最快的方向朝着目标点运动，其受力分析，如图1所示。

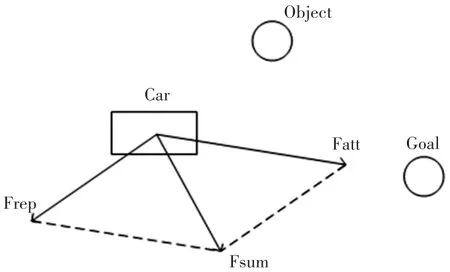
图1 无人车受力分析Fig.1 Stress Analysis of Unmanned Vehicles

传统人工势场法中将受控对象的运动简化为质点运动，运动空间为二维欧式空间，即平面运动，受控对象的位置坐标为X=(x，y)，目标点坐标为Xgoal=(xgoal，ygoal)，目标点对受控对象的引力势场函数为二次函数，即：

式中：k—引力势场系数；Xgoal−X—受控车辆到目标点的距离ρgoal为：

定义环境模型中障碍点位置坐标为Xobject=(xobject，yobject)，则该处斥力势场函数为：

式中：η—斥力势场系数；ρ0—斥力势场影响距离；ρobject—受控车辆到障碍物的距离，当ρobject>ρ0时，车辆不受斥力势场的作用，其中：

受控对象所受总势场为：

式中：n—障碍物的个数。

3 改进人工势场法

3.1 速度斥力势场

为适应实际无人车行驶环境，改善传统人工势场法中动态规划能力差的问题，在改进人工势场模型中加入速度斥力场，其函数为：

3.2 引力势能场

无人车在避障前后都是以主车道线为主要行驶路径，因此以车道中心线为参考，构建车道中心线引力势能场，无人车向车道中心线两侧运动时，引力势能逐渐增加，且增加速度越来越快，其表达式为：

式中：λ—道路中心线引力势能场因子；x0—无人车起点横坐标；ymax—无人车纵向最大位移。

由式（6）和式（1）得出无人车在行驶过程中所受总引力势能为：

无人车所受引力势能的三维分布图，如图2 所示。距离目标点距离越远，引力势能越小，距离车道中心线距离越远，引力势能越大。

图2 引力势能场三维分布图Fig.2 Three−Dimensional Distribution of Gravitational Potential Energy Field

3.3 道路边界斥力场

无人车在实际行驶过程中，在没有其它障碍物的影响时，将受到道路边界的约束，且距离边界越近，所受斥力越大，道路中心线所受边界斥力最小。因此，根据无人车在道路上行驶到任意位置危险系数不同，选用变化程度不同的函数来构建道路边界斥力场。当无人车行驶到两车道中心线之间时，此时距离道路边界较远，危险系数较小，无人车较为安全，选用变化较为平缓的正弦函数构建道路边界斥力场；当无人车行驶到两车道中心线两边时，所受斥力较大，且距离越近危险系数越高，所受斥力变化较快，选用增长较快指数函数构建道路边界斥力场，其表达式如式（8）所示：

由式（8）得到无人车所处行驶于不同位置时所受道路边界势能场的三维分布，如图3所示。无人车距离道路边界越近，斥力势场越大，且变化越快。无人车处于左右车道中心线之间时，势场最小，且变化缓慢。

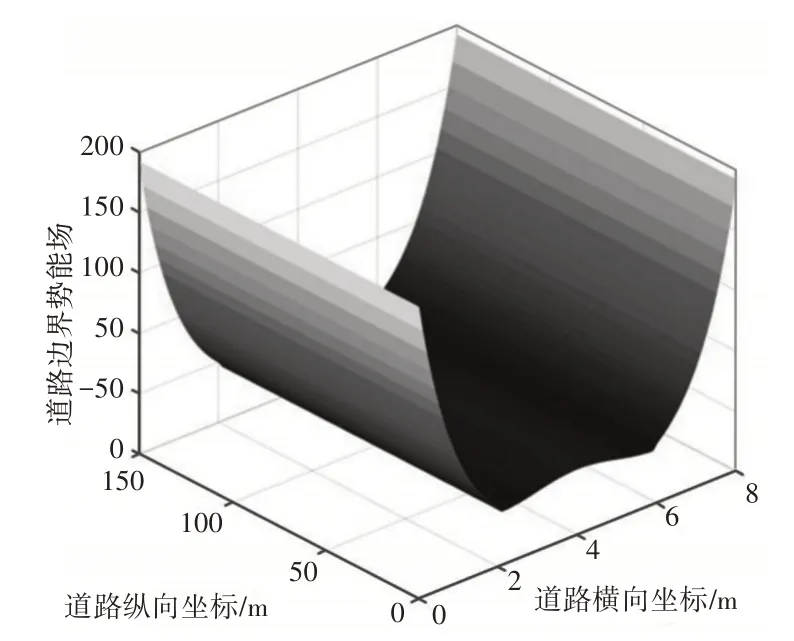
图3 道路边界势能场三维分布图Fig.3 Three−Dimensional Distribution Map of Potential Energy Field on the Road Boundary

式中：γ1，γ2—道路边界斥力场因子；L—道路宽度；xl，xr—左右车道中心线的横坐标。

3.4 障碍物斥力势场

无人车外轮廓近似长方形，在进行路径规划时，考虑路径平滑且无突变的要求，采用椭圆化斥力场边界的概念，若障碍物某一时刻坐标为(xobject，yobject)，将其斥力势场抽象为椭圆函数为：

将式（9）二维椭圆方程通过正态分布函数拓展到三维斥力势能场，其表达式为：

为了简化式（10），取ρ=0，令β=(2πσ1σ2)−1，其表达式变为：

式中：β—障碍物斥力场因子；ρ—横纵向相关系数；σ1，σ2—调节无人车避障路径形状的参数；UP—一个极小的正数。

由式（11）得出不同位置斥力势场能场的三维分布图，如图4所示。

图4 障碍物斥力势场分布图Fig.4 Distribution Map of Obstacle Repulsive Potential Field

因此，无人车在不同位置所受势能场为车道中心线引力场，道路边界线斥力场，障碍物斥力场，速度斥力场以及目标点引力场，其函数表达式如式（12）所示：

4 纯追踪控制器设计

4.1 车辆简化模型

将车辆模型简化为二轮自行车模型[9]，其优势在于简化了前轮转角与后轴所遵循的曲率之间的关系，如图5所示。根据二自由度自行车模型几何关系可得：

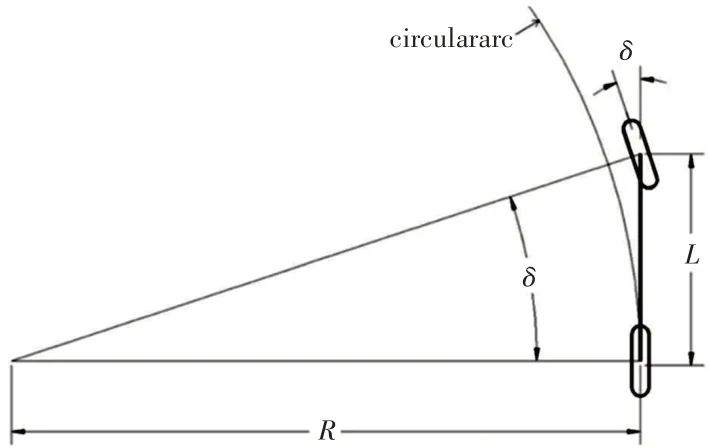
图5 车辆二自由度自行车模型Fig.5 Bicycle Model With Two Degrees of Freedom

式中：δ—前轮转角；L—轴距。

4.2 无人车转向控制

为完成对期望轨迹的追踪，从车辆二自由度自行车模型出发，以后轴为切点，无人车纵向车身为切线，通过控制无人车转角，使得无人车可以按照经过目标点的圆弧行驶[10]，如图6所示。

图6 无人车转向控制原理Fig.6 The Principle of Steering Control for Unmanned Vehicles

图6中(gx，gy)表示无人车要追踪的下一个目标点，α表示当前车身姿态与目标点的夹角，ld表示后轴到目标点的距离，R为转向半径，根据正弦定理得：

前视距离被定义为车速的线性函数，即：ld=εvy(t)，其中：ε—前视系数，vy(t)—无人车纵向速度，则式（15）转化为：

5 仿真实验及结果分析

在无人车二自由度模型中，考虑无人车的当前位置、偏航角度以及无人车的速度，其中速度控制应用简单的P控制器，横向控制采用纯追踪控制器，基于以上原理在Simulink中搭建仿真模型，如图7所示。

图7 纯追踪控制器模型Fig.7 Pure Tracking Controller Model

仿真过程改进人工势场法主要参数，如表1所示。纯追踪控制模型主要参数，如表2所示。

表1 改进人工势场法参数Tab.1 Parameters of Improved Artificial Potential Field Method

表2 纯追踪控制模型主要参数Tab.2 Main Parameters of Pure Tracking Control Model

5.1 静态环境

仿真实验中，设定道路宽度为8m，无人车尺寸为边长1m的正方形，仿真时间间隔为0.1s，无人车起始坐标点为（6，0），终点坐标点为（7，150），障碍物坐标为（6.5，60），设置无人车速度为36km/h，设定移动步长为0.1m，仿真结果，如图8～图9所示。

图8 静态环境无人车规划路径和实际路径曲线Fig.8 Static and Unmanned Vehicle Planned and Actual Path

图9 静态环境无人车规划路径和实际路径横向误差曲线Fig.9 Lateral Error Curve of Planned Path and Actual Path of Unmanned Vehicle in Static Environment

由图8、图9可知改进后的算法能够准确避开障碍物，并且规划路径与实际路径吻合度较高，横向误差最大值为0.015m，横向位置距离右侧道路边界近2m，远大于实际车辆车身宽度一半，说明改进算法能够准确避开静态障碍物，所建立的纯追踪控制模型能够实现安全平稳的跟踪参考轨迹。由图11、图12可以知转角范围控制在±3°内，整体变化平缓，没有突变及震荡情况的出现。无人车实际横摆角曲线与参考线趋势相同，整体偏差较小，说明无人车在路径跟踪过程中稳定性较好，如图12所示。

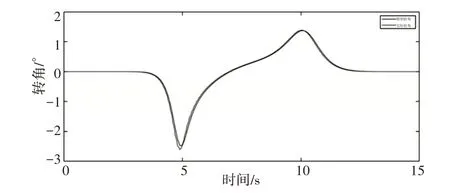
图10 无人车规划转角与实际转角变化曲线Fig.10 Variation Curve of Unmanned Vehicle’s Planned Rotation Angle And Actual Rotation Angle

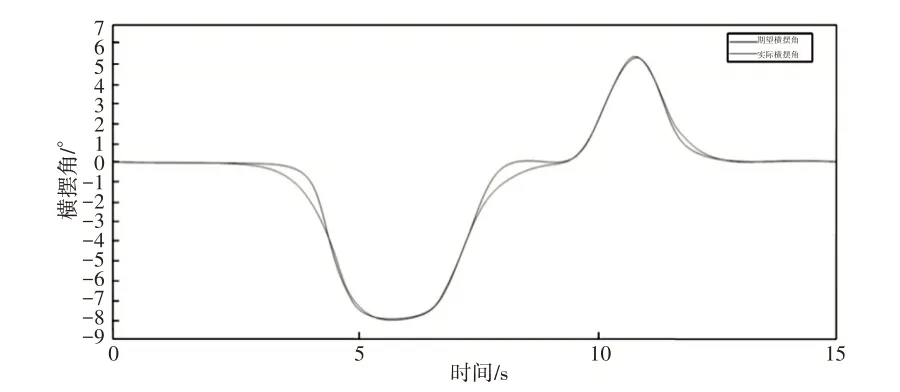
图11 无人车参考横摆角和实际横摆角曲线Fig.11 Unmanned Vehicle Reference Yaw Angle and Actual Yaw Angle Curve

5.2 动态环境

为验证改进算法在动态环境中避障的准确性，在实验中设定移动障碍物初始坐标为（6.5，60），运动方向与y轴正方向夹角135°，速度为36km/h，仿真时间间隔0.1s，设置无人车速度为36km/h，移动步长为0.1m，仿真结果，如图12所示。

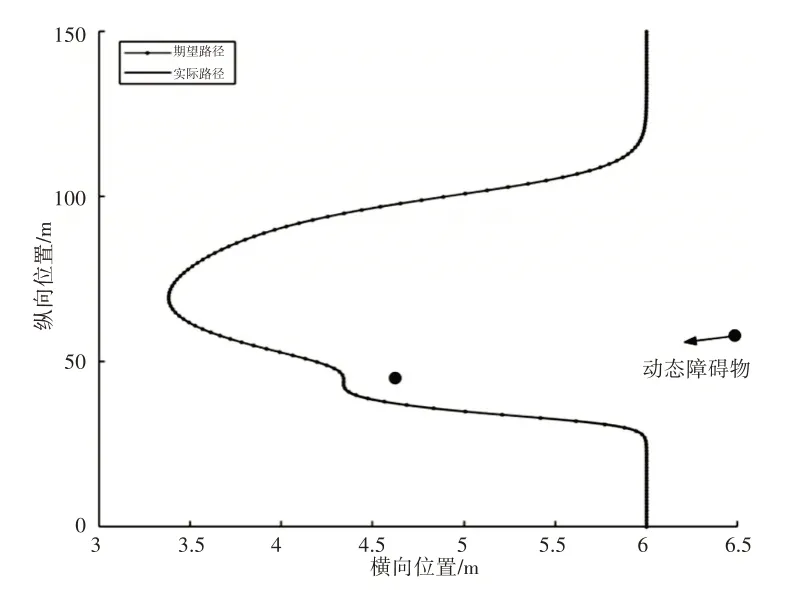
图12 动态环境无人车规划路径与实际路径曲线Fig.12 Unmanned Vehicle Planning Path and Actual Path Curve in Dynamic Environment

由图12及图13可知改进算法在动态环境中能够准确避开障碍物，期望路径与规划路径吻合度较高，横向误差最大值为0.022m，所建立的纯追踪控制器在动态路径规划中能够实现准确追踪。动态环境下无人车转角及横摆角变化曲线，如图14、图15所示。

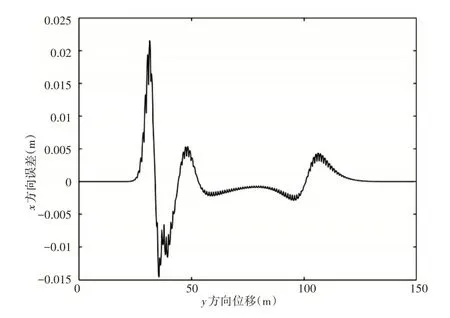
图13 动态环境无人车规划路径与实际路径横向误差曲线Fig.13 Lateral Error Curve of Planned Path and Actual Path of Unmanned Vehicle in Dynamic Environment

图14 无人车规划转角与实际转角变化曲线Fig.14 Variation Curve of Unmanned Vehicle’s Planned Rotation Angle and Actual Rotation Angle

从图中可以看出在出现动态障碍物后无人车开始转向，转角在3°以下，整体变化平稳，无较大范围内突变及震荡。无人车实际横摆角与参考横摆角趋势相同，整体偏差较小，无人车在路径跟踪过程中稳定性较好，如图15所示。

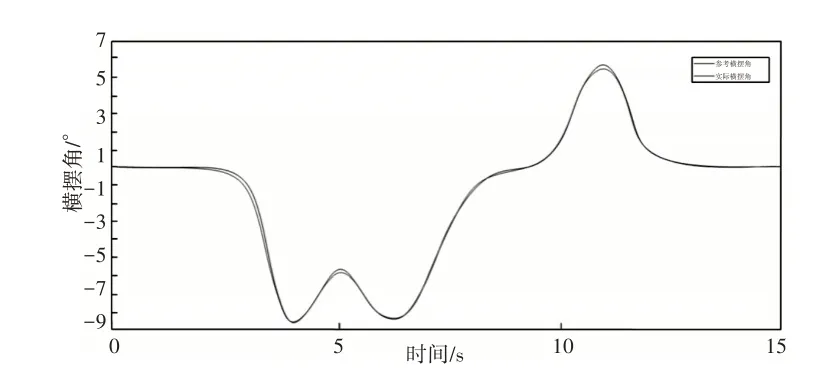
图15 无人车参考横摆角与实际横摆角变化曲线Fig.15 Change Curve of Reference Yaw Angle and Actual Yaw Angle of Unmanned Vehicle

5.3 对比传统人工势场法

基于5.2中的动态环境信息，设置动态障碍物的移动速度分别为18km/h、36km/h、54km/h，在Matlab 中应用传统人工势场法进行仿真结果，如图16、图17所示。

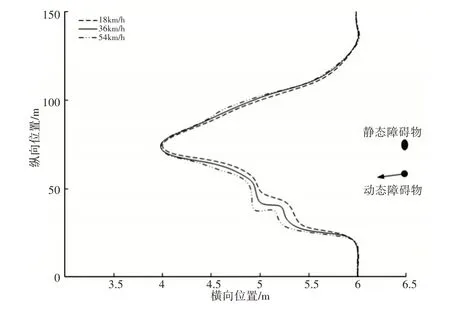
图16 动态环境下传统人工势场法路径曲线Fig.16 Path Curve of Traditional Artificial Potential Field Method Under Dynamic Environment

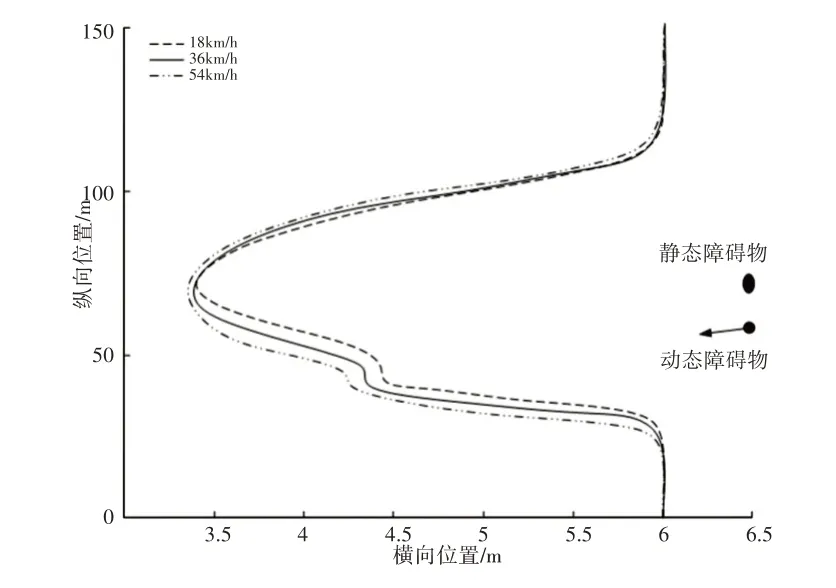
图17 动态障碍物不同速度下改进人工势场法路径曲线Fig.17 Improved Artificial Potential Field Path Curves for Different Speeds of Dynamic Obstacles

由图16可知，在传统人工势场法路径规划中，动态障碍物出现之前，路径平直，效果较好。但当动态障碍物出现后，所规划路径波动较大，并且避开障碍物后，到达目标点之前出现小范围的波动，随着动态障碍物速度的增加，避开动态障碍物的路径抖动幅度越来越大，路径连续波动较明显。由图17可知，改进算法所规划的路径平直，无连续波动，稳定性较高，且随着动态障碍物速度的增加，改进算法规划的路径无大范围波动。对比分析图16、17可知，改进算法在动态避障中路径规划效果较好，且在障碍物不同速度下，路径规划效果较为稳定。

对比分析图12、图16可知，在传统人工势场法路径规划中，动态障碍物出现之前，路径平直，效果较好，但当动态障碍物出现后，所规划路径波动较大，并且避开障碍物后，到达目标点之前出现小范围的波动。改进算法所规划的路径平直，无连续波动，稳定性较高。

5.4 实验平台

拟实验车，该车包括激光雷达、摄像头、毫米波雷达、GPS等传感器以及主流的ADAS控制器，如图18所示。智能小车参数，如表3所示。

图18 实验平台Fig.18 Experimental Platform

表3 智能小车参数Tab.3 Smart Car Parameters

设定智能小车以最大速度行驶，应用改进人工势场法得，如图19所示。智能小车以最大速度行驶时，检测到动态障碍物信息后，能够及时躲避障碍物，准确到达目标点。

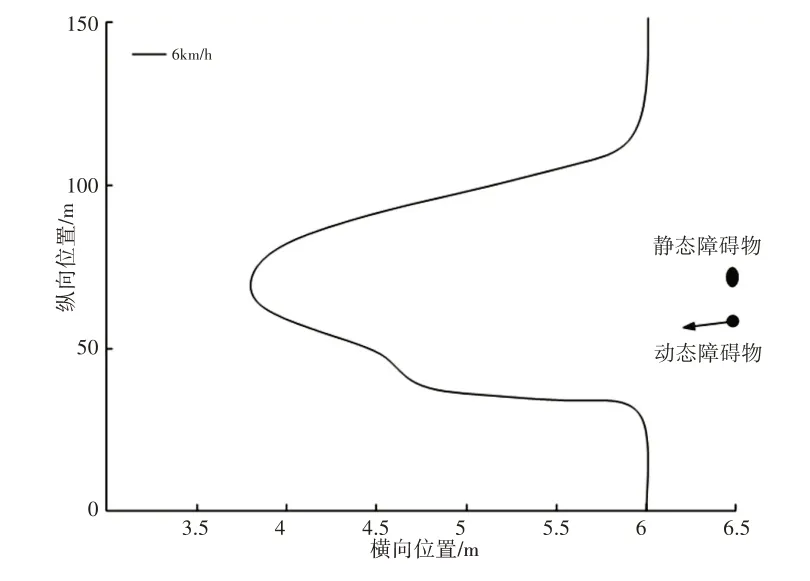
图19 智能小车路径Fig.19 Smart Car Path

6 结论

针对传统人工势场法无法适应于无人车动态路径规划的问题，基于结构化道路改进人工势场法，考虑实际车辆外形的特征，应用椭圆化距离代替斥力势场的中的实际距离，引入道路边界斥力势场模型及车道中心线引力势场模型，从而在较小车道空间内获得局部避障路径，为了更加准确的描述无人车行驶环境及动态障碍物信息，引入障碍物速度斥力势场。在算法的验证上，应用Matlab编程，将车辆模型简化为边长为1m的矩形，添加静态及动态障碍物，建立以转角为控制变量的纯追踪控制模型对所规划的路径进行跟随控制。Matlab仿真及智能小车验证结果表明，在静态及动态环境中，改进算法能够准确避开静态及动态障碍物，与传统人工势场法对比，所规划路径平直，稳定性较高，所建立的纯追踪控制模型能够进行平稳的跟踪控制。