基于井中垂直磁场的可控源电磁法深部矿产探测研究

李棂泽，郭长安，郭俊波，王堃鹏，王向鹏，许 洋

（1.中国安能集团第三工程局有限公司，四川成都 611130；2.中国地质调查局地球物理调查中心，河北廊坊 065000；3.地球勘探与信息技术教育部重点实验室（成都理工大学），四川成都 610059；4.四川省冶勘设计集团有限公司，四川成都 610021）

0 引言

随着国内经济的快速发展，对于矿产资源的需求也与日俱增。以往对矿产资源的勘探与开发主要集中在浅层空间，为获取更多的矿藏资源，亟需加大对深部矿产资源的探测（张竞文和叶丽梅，2018；许逢明等，2022）。随着地质矿产勘查技术的不断进步，综合物探技术已被广泛应用到地质矿产、环境地质等勘查工作中（常振宇，2022）。但由于资源埋藏深，地质构造复杂、异常响应信号弱、抗干扰能力不足等问题，对于地球物理勘查深部矿产资源的技术也面临着更大的考验（滕吉文，2006；马振波等，2022）。

如今，通过观测电磁场的变化情况来探测地下异常体的分布信息已经成为常用的一种电磁探测技术，比如大地电磁法（Magnetotelluric method，MT）、航空电磁法（Z-axis tipper electromagnetic，ZTEM）和可控源电磁法（controlled-source electromagnetic methods，CSEM）。其中，可控源电磁法（CSEM）是利用人工布设场源发射电磁波信号，来探测地下地电结构的一种电磁勘探方法，具有成本低、工作效率高、勘探深度大等优点（Vallée et al.，2011；MacGregor and Tomlinson，2014）。CSEM 作为研究浅中层地质构造的主要地球物理方法之一，被广泛应用于矿产水文普查、地热资源开发、环境工程调查等领域。同时，不同于天然场源，可控源电磁法可以通过人为控制发射频率，较好克服天然源信号弱的缺点，提高数据的信噪比。

近些年来，许多学者相继对可控源电磁法探矿实例和地面典型模型的数值模拟进行了相关研究。张继锋等（2009）基于有限单元法对典型模型进行三维数值模拟，分析了其变化规律。匡海阳等（2012）对长江中下游成矿区开展了不同电磁法探测实验，反演结果有效探明了控矿构造界面，推断了矿体的赋存位置，这对利用电磁法进行地下找矿的实践工作具有十分重要的意义。汤井田等（2014）针对传统有限元数值模拟耗时慢、数据量大等问题，加入无限单元来取代人工边缘条件，在相同计算精度下，提高了数值的计算速度。苏文利等（2015）通过矿区实例，研究了可控源电磁法对深部矿体的探测，指出深部矿体空间定位技术对于深部矿藏资源的勘探与开发具有实质性意义。林方丽等（2016）研究了综合电磁法在矿区深部成矿机制中的应用，进一步验证了可控源电磁法对地质矿床的识别能力。崔中良等（2017）通过综述各个物探方法的应用特点及勘查实例，有效说明了物探在深部金属矿产勘查中具有的独特优势。同时，张林成等（2017）推导了水平电偶极子源的二次场边值问题，实现了更加快速、高精度的CSEM 正演模拟。杨锐等（2019）利用可控源采集的数据得到阻抗信息，进行了有限内存拟牛顿三维反演，得到了可靠的三维电阻率模型。万伟等（2019）对陆地可控源电磁法各场区数据探测效果展开了研究，结果表示近场区和远场区数据的组合有效提升了可控源电磁反演效果。圣安陈等（2020）基于有限内存拟牛顿法反演算法，对可控源数据进行三维反演计算，成功探明了地下三维电性构造，圈定出了成矿区域。韩思旭等（2021）研究了地面频率域可控源电磁法的多源联合反演，发现不同源的组合方式可以改善地面反演效果。

以往研究已证明可控源电磁法对地下矿床的有效识别，但受限于地面勘探所能达到的深度和精度，难以较好地查明深部矿藏位置信息，存在着分辨率不足甚至无法识别异常等问题。本文利用矿区已有矿井，测量井中深部垂直磁场信息，采用交错网格有限差分法实现了三维正演数值模拟，对比分析矿井相对异常体不同位置所带来的异常响应。采用有限内存拟牛顿法（LBFGS）实现了快速三维反演，算例中加入的地面可控源三维反演也较好地说明了本文算法的正确性和井中深部探矿的必要性。为达到对地下矿体全方位（深部与浅层）同时识别的目的，结合矿井测点和地面测点正演数据实现三维联合反演，为实际探矿工作提供了可行的方案。

1 CSEM正演理论

在大部分电磁法勘探工作中，选取的采集频率都相对较低。对于大多数传播介质而言，位移电流的影响可以忽略不计。因此，本文含电性源的CSEM三维正演问题中，当取时谐因子为e-iωt，频率域的麦克斯韦方程组可以表示为（Li and Key，2007）：

式（1）～（2）中，Js是外加电性源的电流密度，A/m2；σ是电导率，S/m；μ0是真空磁导率，H/m；ω是角频率，rad/s。

简单代换（1）、（2）两式，可以得到关于电场强度E的表达式：

对于CSEM 来说，考虑到Js是一个奇异点，会给三维数值模拟带来困难。因此，引入一个背景参考模型σr，同样满足上述方程，通过采用总场减去背景场的方式，避免此项在三维离散方程中的影响，得到的二次场偏微分方程如下（Weiss and Constable，2006）：

其中背景场的计算参考Key（2009）Dipole方法，式（4）中σr为背景电导率，Er为背景电场，Es为二次场。

本文求解上式方程选取的方法是交错网格有限差分法，基于Yee网格，将研究区域离散为长方体单元结构，将磁场采样点放在单元面中心点上，电场采样点放在单元体棱边中点位置，如图1a所示。

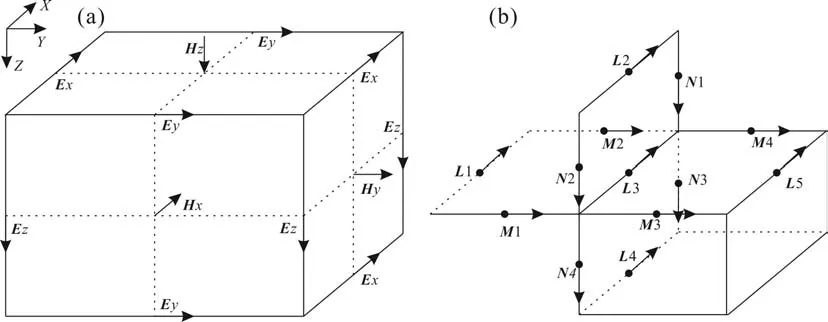
图1 网格剖分图Fig.1 Grid division diagrams

进一步将上式展开为以下分量形式：

式（8）中，∆y'j=(Δyj-1-Δyj) 2，∆z'k=(Δzk-1-Δzk) 2，另外两个关于y分量和z分量有类似离散方式（杨波，2012）。边界条件通过一维MT 解析解获得，在离散长方体单元结构的棱边上写出电场各个分量满足的方程式，最终得到一个关于电场强度的正演方程：

式（9）中，K为差分系数矩阵，E为网格单元棱边待求电场值，B为离散化的右端项，边界值及场源有关的列向量。采用QMR 方法求解上式（Freund and Nachtigal，1991）。

本文的正演基于王堃鹏等（2021），无人机频率域半航空电磁法三维反演，相关正确性验证工作不再赘述。

2 反演理论

在地球物理三维电磁反演中，为了降低反演过程中存在的多解性问题，常常采用的方法是利用正则化方法来约束目标函数的模型项，以此来获得稳定的最优解，即由观测数据和约束条件共同构成的反演目标函数。本文为了提高反演的敏感度，以对数的方式约束反演参数，让所计算出来的参数结果都为正数。同时加入先验模型，使得模型稳定在所设定的先验模型附近。具体的目标函数表达如下（Egbert and Kelbert，2012）：

式（10）中：λ为正则化因子，C-1d为加权矩阵，C-1m为模型的约束矩阵，m0为先验模型。

进一步求导可得到如下梯度表达式（Kelbert et al.，2014）：

这里给出灵敏度矩阵表达式：

其中d1，d2…dn，是不同的正演数据，Nd是观测数据个数，Nm是模型参数个数。

可以得知，整个灵敏度矩阵需要进行大量的正演计算，然而三维反演利用差分法近似计算灵敏度矩阵难以实现。本文所使用的反演方法是有限内存拟牛顿法（LBFGS），上式中出现的灵敏度矩阵J并不直接求解，而是采用Rodi and Mackie（2001）和Newman et al.（2010）的一种巧妙的方法快速得到梯度，避开了灵敏度矩阵的计算。

将目标函数扩展到多元函数，表达为：

式（13）中[Hk]为海森矩阵，g(mk)为目标函数梯度。

然而对于实际的三维反演工作来说，计算海森矩阵的逆十分困难，存储空间要求巨大。因此数学家提出BFGS 方法，通过前几次迭代的目标函数逼近海森矩阵的逆，可以达到高效快速的优点。本文中所使用的LBFGS 方法在BFGS 的基础上，依据Byrd et al（.1996）给出的一种双循环递归隐式直接求取[Hk]-1g(mk)，表现如下：

（5）Hkgk=r

有限内存拟牛顿法（LBFGS）的思路在于对计算当前迭代需要的海森矩阵逆，无需存储[Hk]-1，采用前（3～20）次迭代目标函数梯度逼近，节省大量的存储空间，达到快速反演的效果（Nocedal et al.，2006）。LBFGS步骤如下：

步骤1：确定初始计算模型m0，设定相关反演参数（最大迭代次数和最小拟合差），以及正则化因子的参数；

步骤3：设定初始步长，进行一维线性搜索寻找最佳迭代步长α，步长满足wolfe条件。获得迭代模型：

mk+1=mk+αpk

步骤4：验证当前模型迭代最小拟合差或最大迭代次数是否满足反演参数设定，若满足任一条件，则停止反演。反之，返回步骤2，继续迭代。

3 井中垂直磁场响应分析

本文的研究基于矿井深部垂直磁场信息，对地下异常体做正演响应分析。如图2所示，将长导线人工源布设在（0 m，-8100 m）的位置，长度1000 m，与x轴平行。地下异常体埋深500 m，大小为250 m×250 m×100 m。正演算例中分别选取10 Ω ⋅m，100 Ω ⋅m，1000 Ω ⋅m的异常体来分析不同电阻率值异常体所呈现的正演响应。图2中矿井1，2，3，4代表着相对于异常体不同井的位置。矿井1位于（0 m，0 m），矿井2位于（0 m，100 m），矿井3 位于（0 m，200 m），矿井4 位于（0 m，400 m）。井深700 m，正演垂直测点距离按照10 m 等距进行测量。背景电阻率设置为200 Ω ⋅m，选择350 Hz频率下进行对比分析。

图2 井中可控源电磁法工区数据采集示意图（矿井1，2，3，4）Fig.2 Schematic diagrams of data acquisition by the borehole controllable source electromagnetic method in the work area（boreholes 1， 2， 3 and 4）

图3 所示为350 Hz 频率下的不同参数井中正演响应，3a 和3b 是均匀半空间条件下，BZ实虚部响应随着深度的变化情况。在地下无异常体的情况下，对于不同测点，实部和虚部的响应曲线都表现得十分平滑。但对于地下存在异常体的情况下，相同电阻率模型正演响应的实部与虚部均在深度500～600 m 出现异常波动，与实际真实模型的深度位置比较接近。其中矿井2 位置相较于其它矿井中采集的磁场信息所带来的异常波动最为突出，说明垂直磁场BZ对于地下异常体边界位置的识别更加灵敏。如图4 所示，将井中正演数据与均匀半空间模型正演数据进行实部与虚部的相对误差计算。为了避免浅层地面测量数据所造成的影响，相对误差的计算舍弃了前50 m 的数据，主要针对地下深部空间异常响应的分析对比。可以发现，由于矿井1 测点位置位于异常体的中心点，即使异常体电阻率值发生了变化，整体相对误差一直都趋于零。这是由于磁场受到异常体的影响，在其中心点位置磁场响应较弱。另外，异常体电阻率值的改变同样影响着异常响应的强弱，所需探明矿体的电阻率值与正演所选用的背景电阻率越接近，异常响应越弱。

图3 不同电阻率异常体井中正演响应图Fig.3 Forward modeling response of abnormal bodies with different resistivity

图4 不同电阻率异常体井中正演实部相对误差和虚部相对误差Fig.4 Real and imaginary relative errors of forward modeling in boreholes with different resistivity anomalies

4 反演算例

本节对不同深度的低阻体进行反演试算，依据上述正演结果，设置地下低阻体电阻率为10 Ω ⋅m，并且将钻井测点位置靠近异常体的边界，以达到更好的反演结果。本文的反演算例选取的频率为1000 Hz、600 Hz、350 Hz、200 Hz、100 Hz、25 Hz，对正演数据均加入3%的随机误差，实现了如下四种反演算例：

（1）基于地面测点正演数据，实现地面可控源三维反演；

（2）基于井中测点正演数据，实现井中可控源三维反演；

（3）将地面反演的最终迭代模型作为井中测点正演数据的反演初始模型，实现先地面后井中的可控源三维反演；

（4）结合地面测点正演数据和井中测点正演数据，放入同一个梯度函数，对均匀半空间初始模型进行可控源三维反演。

图5所示为两个低阻体在不同深度的真实模型示意图，背景电阻率设置为200 Ω ⋅m，低阻体均为10 Ω ⋅m。低阻体大小均为250 m × 250 m × 100 m，浅部低阻体埋深100 m，深部低阻体埋深500 m。模型网格中心区域x和y方向按照50 m大小进行均匀剖分，共计29个网格。z方向在浅层做细分处理，降低电阻率的剧烈变化带来的影响，提高反演精度。依照20 m的间隔距离剖分到700 m的深度，随后依照倍数递增，外延网格区域。地面测量的测点选择在剖分网格中心位置，共计841个，井中测量测点由浅到深按照10 m的间距采样，共计71个测点数。其中，井中测量所选取的矿井位置在（0 m，400 m）的位置，靠近深部低阻体右边界中心区域。

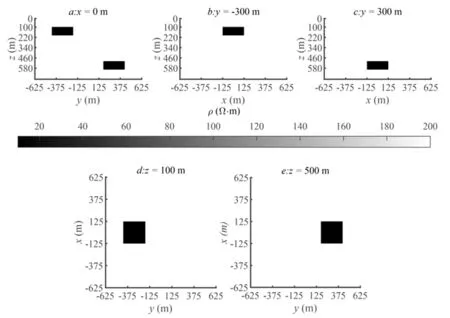
图5 反演算例真实模型切片图Fig.5 Real model slice diagrams of inversion examples

首先开始第一个反演算例的计算，基于地面测点正演数据，对均匀半空间初始模型反演成像。经过49 次迭代得到如图6 的反演结果，反演结果与真实模型的对比可以看出，对于浅层低阻体的识别效果较好，低阻体中心区域电阻率的恢复比较接近真实模型，依照不同切片图也能够判断出浅层地电模型的三维空间位置信息。但对于深度500 m 的低阻体识别就基本上没有任何信息，无法对深部地电模型进行位置判断。结果表明LBFGS 反演算法对本文的三维CSEM 反演是正确的，但是地面测点数据有限于趋肤深度的影响，对较深的异常体识别太弱，这也为下一步井中测量的研究做了铺垫。

图6 地面测点数据反演结果（反演算例1）Fig.6 Inversion results of ground measurement point data （inversion example 1）

针对地面反演对深部空间识别较弱的问题，本文进行了第二个反演算例的计算。矿井中垂直磁场分量按照10 m等距进行采集，采集点共计71个。地下异常体真实模型同算例1，设置与地面测量同等参数，经过107次迭代，得到如图7反演结果。切片图中直观的看出深部低阻体的有效识别，而浅部异常体由于钻井位置距离较远，即使埋藏深度较浅，探测效果依旧很差，这也是井中磁场数据反演识别的不足。相对于地面测量反演结果，井中磁场数据对于深部异常体的探测十分明显，极大地提高了深部空间识别的分辨率，能够实现局部高精度的矿产勘探。

图7 井中测点数据反演结果（反演算例2）Fig.7 Inversion results of borehole measuring point data （inversion example 2）

在以上研究结果的基础上，发现地面和井中反演都有着各自鲜明的优势和劣势。因此，进一步开展了算例3和算例4的反演计算，对地下不同深度的异常体探测进行研究分析。算例3将地面测量数据最终反演迭代模型作为井中三维反演的初始模型，来增加对浅层地质构造信息的控制。经过94次迭代，得到如图8的反演结果。无论是浅层低阻体的识别，或是深部异常体的探测，都得到了一个较好的反演结果。异常响应区域足够集中，与真实模型位置较为吻合。算例4结合地面测点正演数据与井中测点正演数据，放入同一个梯度函数，对均匀半空间初始模型进行三维反演。结果如图9所示，经过91迭代，依旧得到了一个显著的反演效果，有效识别出了两个低阻体的位置。以上的四个算例反演研究可以说明，对于CSEM三维反演，井中垂直磁场数据可以极大提高对深部空间探测的分辨率。同时，地面与井中的联合反演可达到对地下不同深度异常体识别的目的。最后，图10拟合差曲线图显示反演收敛明显，迭代速度快，实现了快速的三维反演，说明了本文算法的可行性和高效性。

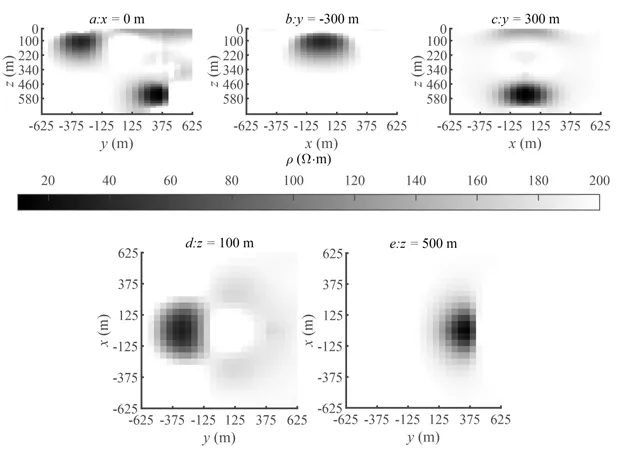
图8 先地后井反演结果（反演算例3）Fig.8 Inversion results of ground first and then borehole （inversion example 3）

图9 地井数据联合反演结果（反演算例4）Fig.9 Joint inversion results of ground and borehole data （inversion example 4）

图10 四个反演算例拟合差迭代曲线图Fig.10 Four inversion examples fitting difference iterative curve graphs

5 结论

本文以深部空间矿产资源勘探为研究背景，通过采集矿井中垂直磁场数据来有效识别地下异常构造的分布位置。针对不同矿井位置和不同电阻率值的地质体，实现了有限差分三维正演响应，认识到井中垂直磁场数据的响应特点。同时，对不同深度的低阻异常构造开展三维反演数值模拟工作，进一步了解到井中磁场数据的有效性，具体总结如下：

（1）地下异常体电阻率值与背景电阻率值的差异化越大，异常体的正演响应特性更加明显。

（2）井中磁场数据对异常体边界的反映比较强烈，矿井位置越靠近边界，响应愈发突出。

（3）对于深部地层的探测识别，井中磁场数据的反演效果较好，获得的地层信息更加丰富。

（4）地面数据和井中数据的三维联合反演有效的提高了对不同深度异常构造的探测分辨率。

本文基于井中深部垂直磁场的CSEM 三维正反演工作为深部开采矿藏资源提供了有效参考依据，弥补了可控源电磁法探矿对深部空间识别不足的缺陷。

［附中文参考文献］

常振宇.2022.地球物理勘查技术在矿山深部找矿中的应用［J］.世界有色金属， （17）：58-60.

崔中良，刘洋，姚艳领，程金华，晏铭.2017.浅析物探在深部金属矿产勘查中的应用［J］.河北地质大学学报，40（5）：13-19.

韩思旭，陈卫营，薛国强，雷康信，宋婉婷.2021.频率域可控源电磁法多源数据联合反演［J］.地球科学与环境学报，43（6）：1057-1068.

匡海阳，吕庆田，张昆，严加永，陈向斌.2012.多种电磁测深技术在深部控矿构造探测中的应用研究——以泥河铁矿为例［J］.地质学报，86（6）：948-960.

林方丽，王光杰，杨晓勇.2016.综合电磁法在矿区深部成矿机制中的应用研究——以皖南乌溪多金属矿区为例［J］.地球物理学报，59（11）：4323-4337.

马振波，杨骁，苏永锋，李志勋，蔡仲明，李肖龙，裴中朝.2022.河南栾川矿集区深部资源综合物探找矿勘查［J］.地质与勘探， 58（4）：846-856.

圣安陈，杨悦，李亚彬，邹宗霖，翁爱华.2020.可控源电磁法三维反演在甘肃花牛山铅锌矿勘查中的应用［J］.世界地质，39（4）：878-887.

苏文利，刘瑞德，陆桂福.2015.可控源电磁测深方法勘查深部隐伏矿体应用实例［J］.工程地球物理学报， 12（3）：299-303.

汤井田，张林成，公劲喆，肖晓.2014.三维频率域可控源电磁法有限元-无限元结合数值模拟［J］.中南大学学报（自然科学版），45（4）：1251-1260.

滕吉文.2006.强化开展地壳内部第二深度空间金属矿产资源地球物理找矿、勘探和开发［J］.地质通报， 25（7）：767-771.

万伟，唐新功，黄清华.2019.陆地可控源电磁法探测效果的频率响应［J］.地球物理学报，62（12）：4846-4859.

王堃鹏，罗威，曹辉，王绪本，蓝星，段长生.2021.无人机频率域半航空电磁法三维反演［J］.地球物理学报，64（5）：1759-1773.

肖庆辉，施俊法，刘树臣.2003.国外矿产资源研究的主要发展趋势［J］.国土资源情报，（12）：1-4.

许逢明，赵院冬，李成立， 崔健， 吴大天， 孙巍.2022.黑龙江多宝山矿集区三维地质建模与深部找矿预测［J］.地质与勘探， 58（3）：629-652.

杨波.2012.考虑地形的海洋电磁可控源电磁三维数据正反演 ［D］.武汉：中国地质大学（武汉）：1-98.

杨悦，翁爱华，张艳辉，李世文，李建平，唐裕.2019.基于可控源电磁法阻抗信息的有限内存拟牛顿法三维反演［J］.吉林大学学报（地球科学版），49（2）：591-602.

张继锋，汤井田，喻言，王烨，刘长生，肖晓.2009.基于电场矢量波动方程的三维可控源电磁法有限单元法数值模拟［J］.地球物理学报，52（12）：3132-3141.

张竞文，叶丽梅.2018.试述物探技术在地质找矿与资源勘查中的应用［J］.世界有色金属，（12）：109-110.

张林成，汤井田，任政勇， 肖晓.2017.基于二次场的可控源电磁法三维有限元-无限元数值模拟［J］.地球物理学报，60（9）：3655-3666.