基于自适应控制系统的智能车横向轨迹跟踪控制

张志豪 鲁雅阁

（重庆交通大学机电与车辆工程学院，重庆 400000）

主题词：模型参考自适应控制 自适应PID 车辆动力学模型 横向控制

1 引言

自动转向系统是车辆运动控制的核心技术之一，而横向轨迹跟踪控制是目前研发自动转向系统的核心内容，即在保证稳定性和安全性的前提下，要求车辆根据规划层的实时输出和车辆的实时状态反馈精确跟踪参考路径点行驶。因此，在智能汽车轨迹跟踪控制中，跟踪精度始终是一个技术难点。

目前针对这些技术问题，相关学者针对车辆横向轨迹跟踪控制技术开展了大量研究，已经取得一定的成果。主要成果有模型预测控制（Model Predictive Control, MPC）、滑模控制、比例-积分-微分（Proportional-Integral-Derivative Control, PID）控制、模糊控制、自适应控制和自抗扰控制。Li 等[1]考虑了不同驾驶风格对轨迹跟踪的影响，基于人工势场法（Artificial Potential Field,APF）对不同驾驶风格进行轨迹规划，然后基于MPC控制器对所规划的路径进行轨迹跟踪，虽然可以保证不同驾驶风格的车辆控制稳定性问题，但是对于横向误差的控制精度还有待提升。李伟等[2]设计了基于准滑模控制策略设计路径跟踪控制器，并将该控制策略利用dSPACE 对其进行硬件在环（Hardware In the Loop,HIL）验证，结果表明准滑模轨迹跟踪控制在追踪期望路径时，由于外界干扰等在存在一定偏差。

Chen等[3]提出了一种基于自适应模糊PID控制算法的路径跟踪控制器，这种控制方法可以保证不同工况下跟踪期望轨迹的准确性，同时也具有一定的鲁棒性，但系统的实时性有较大波动。Cheng等[4]设计出一种基于侧向偏差的自适应滑模控制方式，滑模控制器抖振由引入一种可随滑模面和系统跟踪误差的切换函数增益值来抵消。Wu 等[5]提出了一种基于非奇异终端滑模和自抗扰控制（Active Disturbance Rejection Control, ADRC）的鲁棒自动导引车路径跟踪控制策略。这种控制方法能在保证车辆稳定性前提下快速准确地跟踪参考路径，但在速度变化较大时无法满足紧急驾驶条件下的路径跟踪要求。

通过对横向轨迹跟踪方法研究发现：由于车辆系统较为复杂，会降低控制算法实时性，同时所产生的横向跟踪误差也将变大；而在横向轨迹跟踪中，控制算法在不同工况下适应能力较弱。针对这一问题，对模型参考自适应控制策略进行了研究，并将其与PID控制器相结合，并设计了PID 控制器参数的自适应律。仿真结果表明，该方法能够使系统较为准确地跟踪，参考模型的输出鲁棒性良好，具有一定的实用价值。

2 车辆动力学模型建立

在用于验证控制器的仿真环境中，过于复杂的车辆动力学模型反而会影响控制器的实时性和精度，从而达不到预期的控制效果。本文通过设计控制算法使车辆快速稳定地跟踪预设的参考轨迹。因此，车辆动力学模型在保证精确描述车辆状态的前提下，应尽可能简化，以保证控制算法的实时性并降低控制器设计难度。

本文根据车辆横向控制的特点，将前轮转向的四轮车辆简化为两轮自行车模型。研究结果表明，车辆在普通路面行驶时该模型有效。在动力学建模时做出如下假设：

（1）假设车辆为刚体，忽略悬架的作用；

（2）假设忽略左右轮载荷变化对轮胎侧偏特性影响；

（3）假设轮胎仅受纯侧偏力影响，不考虑轮胎纵向受力；

（4）假设车辆的纵向车速Vx恒定不变。

图1是由前后2个有侧向弹性的轮胎支撑于地面并具有侧向及横摆运动的二自由度汽车动力学模型[6]。

图1 线性二自由度汽车动力学模型[6]

本文只考虑车辆横摆运动和侧向运动来搭建2自由度的车辆动力学模型。

如图2所示，Vx、Vy为t时刻质心速度V在X、Y轴上的分量，且Δθ很小。在t+Δt时刻有：

图2 车辆运动分析

式中，ΔVX，ΔVy分别为t+Δt时质心速度V在X、Y轴上的分量的变化量；Δθ为车辆质心侧偏角。

车辆坐标系下的质心纵侧向绝对加速度ax、ay为：

由轮胎的侧偏特性为：

式中，Kf、Kr为前后轮侧偏刚度；δf、δr为前后轮转角。

前文已假设Vx恒定不变，结合式（3）～式（5），整理得：

则可得系数矩阵A为：

由式（6）、式（7）可知控制系统的状态空间方程为：

式中，X为状态向量；A为系统矩阵；B为控制矩阵。

3 MRAC-PID横向轨迹跟踪控制器设计

3.1 PID控制方法

PID控制器作为一种线性控制器，因其原理简单、适用性强、参数整定灵活和鲁棒性强的优点而被广泛应用于工业过程控制中（图3）。但由于PID控制器的性能受到3个参数的影响，经过多年的发展，已有了较为成熟的参数整定方法，如Ziegler-Nichlos 频率响应法、过程反应曲线法等[7]。

图3 PID控制系统

如图3所示，典型的PID控制器可表示为：

利用工程整定法对控制系统直接进行参数在线整定，利用MATLAB 中的控制系统设计器（Control system designer）软件，以阶跃信号作为动态响应输入。通过伯德图、根轨迹和阶跃响应分析系统的稳定性，并对补偿器进行在线调节或添加零极点重新设计补偿器以达到期望的控制效果。参数整定后系统的伯德图及阶跃响应如图4 所示。此时响应时间为0.000 3 s。PID控制器的参数初始值取：Kp=20；Ki=0.9；Kd=1。

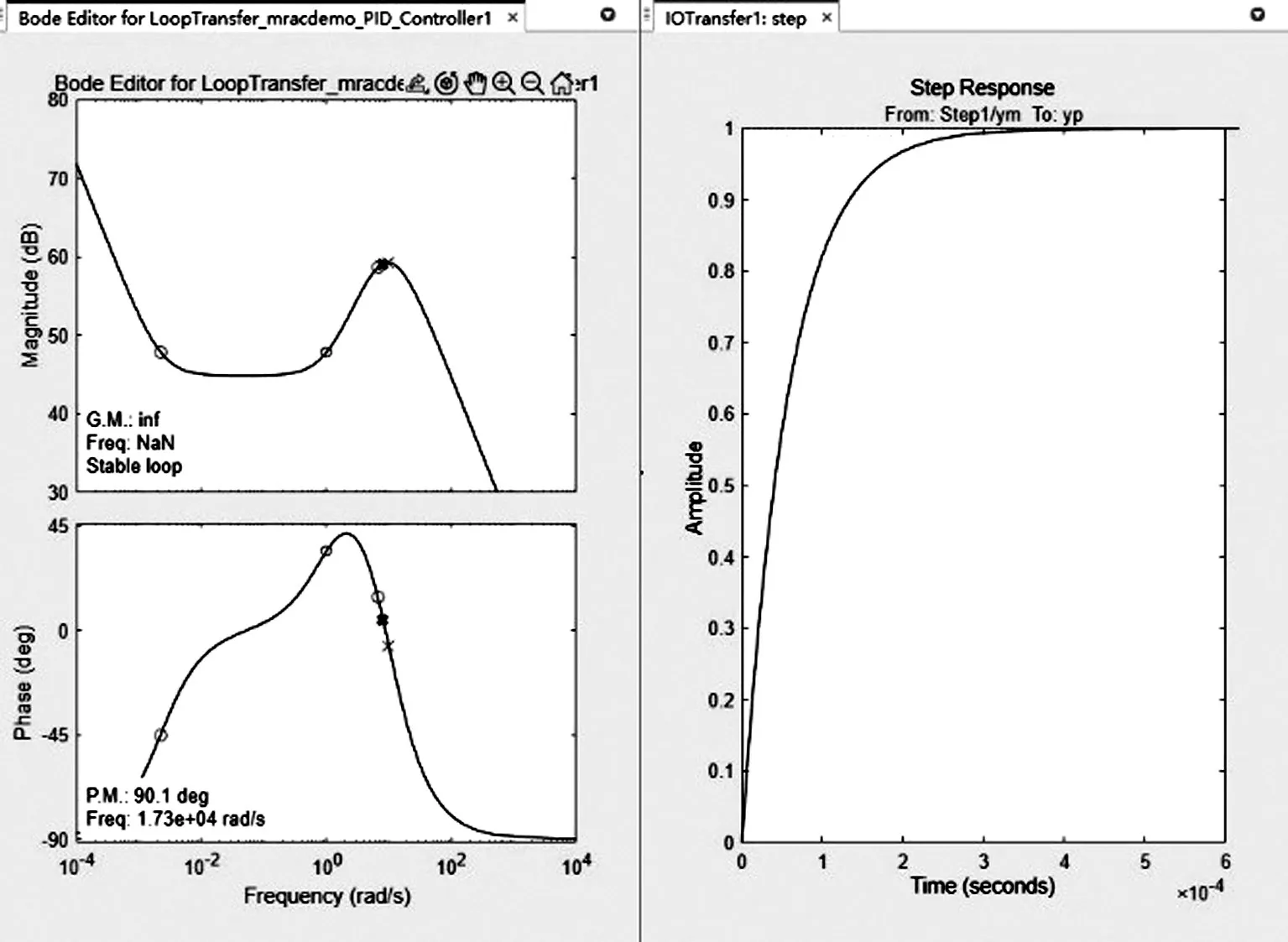
图4 PID控制系统伯德图和阶跃响应

3.2 基于模型参考自适应的PID控制器设计

模型参考自适应控制（Model Reference Adaptive Control,MRAC）系统作为一种自适应控制系统，主要由不确定被控对象、参考模型、控制器和自适应律组成（图5）。这种自适应控制系统已经有较为成熟的分析综合理论和方法，并在航空航天等领域中获得了广泛应用[8]。

图5 模型参考自适应控制（MARC）系统结构

模型参考自适应控制系统设计的核心问题是如何设计自适应律。MRAC系统的设计方法有2种：

（1）基于局部参数最优理论进行设计

局部参数最优化理论最早由Whitaker 等[9]提出，又称为麻省理工学院律（Massachusetts Institute of Technology of law，MIT 律）。该方法的特点包括：所使用输出偏差和自适应律所需信号易获取、一阶系统的性能指标函数按指数级快速收敛到自适应律目标内，在有限时间内系统跟踪参考模型达到稳定。

（2）基于稳定性理论设计

此方法基于保证系统稳定性的角度选取自适应律，使系统具有更好的动态特性。

3.2.1 模型参考自适应控制策略

由式（8）定义一阶单输入单输出（Single Input Single Output,SISO）系统[10]：

控制策略的最终目标是基于Lyapunov 稳定性理论，选取一个不含偏差导数的自适应控制率，并利用此控制率输出一个有界控制输入信号，使得广义输出误差e(t)最终满足lti→m∞e(t)=0。控制器中的可调参数最终保证控制目标的实现[9]。在式（17）中，如果满足p≤n-m,n-m是控制对象的相对阶次，且自适应增益γ＞0，参数反馈增益α≥0；r(t)为有界函数且存在函数r(t)的（q+1）阶微分，则自适应控制器可达到目标lti→m∞yr(t)-r(t)=0 和|δ(t)|≤Δ[10]。

3.2.2 模型参考自适应PID控制策略

将上述PID 控制器作为自适应误差信号δ(t)的结构形式,即：

由式（17）和式（18）可得模型参考自适应PID 控制器的自适应律[11]：

根据式（20）PID的自适应律得到的PID控制可调参数，将参数代入式（19）便得到基于模型参考自适应的PID控制器，系统结构如图6所示。

图6 模型参考自适应PID控制系统结构

4 控制器仿真对比分析

4.1 仿真工况与参数设置

为验证本文所设计的MRAC-PID 横向跟踪控制器对车辆行驶状态的适应性，基于MATLAB/Simulink平台建立仿真模型。将第1节中的车辆动力学模型作为被控对象，车辆基本参数如表1所示。

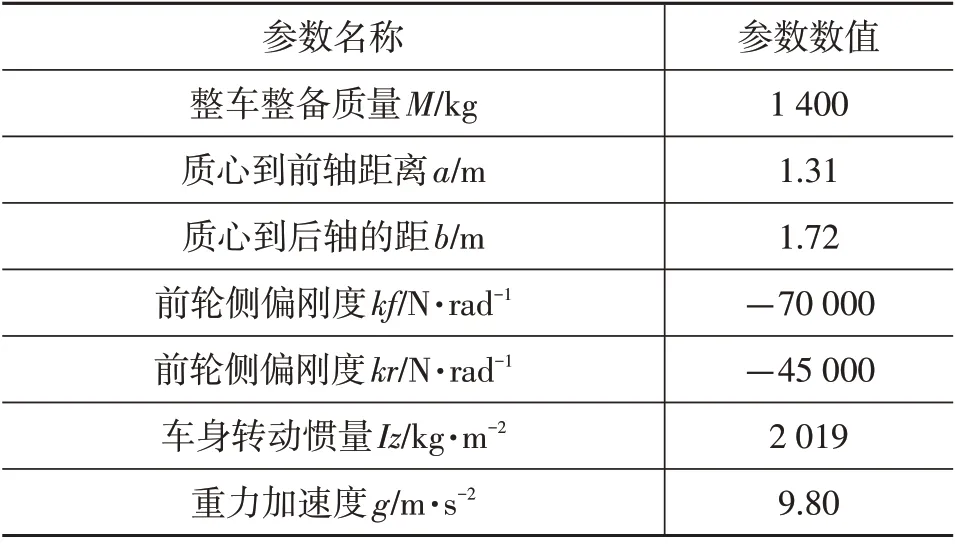
表1 车辆基本参数表

仿真路径以MATLAB Function 模块嵌入模型中，纵向路程为200 m，如图7所示。

图7 参考路径

4.2 仿真对比分析

为验证模型参考自适应控制解决PID 参数整定困难和鲁棒性差而导致的控制性能下降问题，本文建立了PID 控制系统仿真框图，旨在与基于模型参考自适应的PID控制系统仿真框图进行仿真对比，如图8、9所示。

图8 PID控制系统仿真

图9 参考自适应PID控制系统仿真

（1）工况1仿真

参考路径如图10所示，在Simulink中将车辆纵向速度设为10 m/s，车辆初始位置为（0，0），h横摆角度为0°，以前轮转角作为控制输入，以车辆横向速度及车身横摆角为输出。设置相关参数后，进行对上述参考路径的轨迹跟踪，此工况下的仿真结果如图10～图12所示。

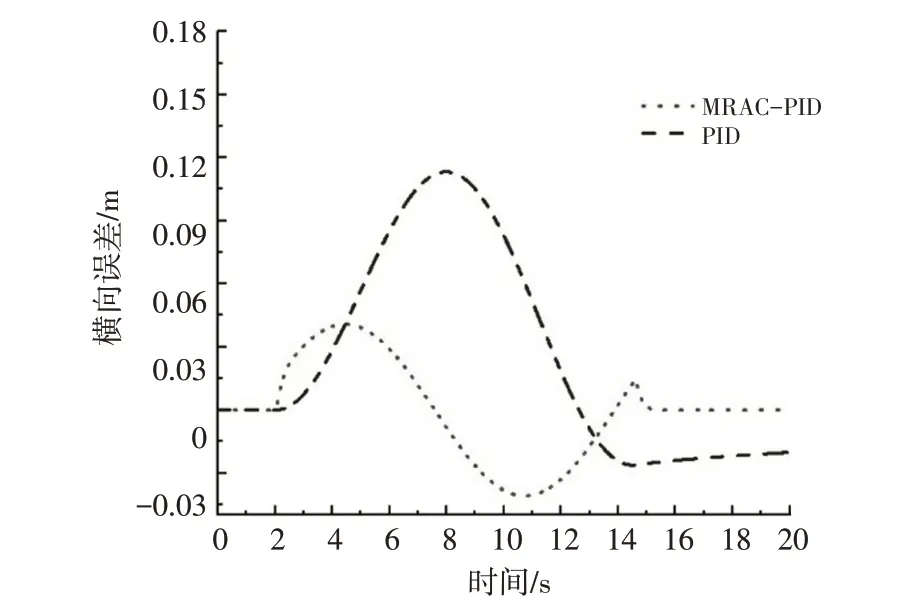
图10 横向位置跟踪效果

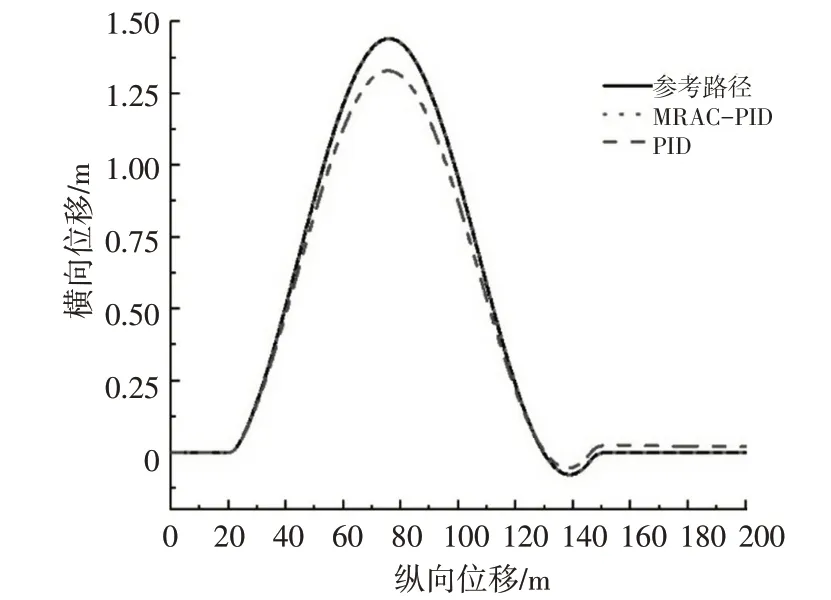
图11 位移跟踪误差

图12 横摆角跟踪误差

图10、图11 为工况1 横向位移的跟踪效果，由图10 可以看出2 个控制器均能较好的跟踪参考路径，且无太大波动与偏差。由图11 横向位置跟踪误差可看出，基于MRAC 的自适应PID 控制器更为稳定，在时间t为4.3 s 和10.9 s 时，横向跟踪误差达到2 个极值，约为0.034 m 和-0.036 m，整体误差也在此范围内波动，15.2 s 后跟踪误差为0。而PID 控制器在8.35 s 达到最大超调量，约为0.118 m。由图12横摆角跟踪误差可以看出，MRAC-PID 控制器的最大横摆角误差为0.038 rad，远低于PID 控制器的0.067 rad，同时，PID 控制器的横摆角误差最终未趋于稳定。以PID 控制器的误差为基准，基于MRAC 的自适应PID 控制器使横向位移误差减少了52.10%，使横摆角误差减少了11.90%。故在10 m/s 的工况下，MRAC-PID 控制器的横向位置跟踪精度要明显优于PID控制器。

（2）工况2仿真

参考路径如图13所示，在Simulink中将车辆纵向速度设为20 m/s，车辆初始位置为（0，0），横摆角度为0°，以前轮转角作为控制输入，以车辆横向速度及车身横摆角为输出。进行对参考路径的轨迹跟踪仿真，在工况2下的仿真结果如图13～图15所示。

图13 位移跟踪效果

图14 横向位置跟踪误差

图15 横摆角跟踪误差

图13和图14为工况2下的横向位移跟踪效果，由图13可以看出2个控制器均能较好地跟踪参考路径，且无太大波动与偏差。由图14横向位置跟踪误差可以看出，基于MRAC的自适应PID控制器更为稳定，在时间t为2.2 s和5.35 s时，横向跟踪误差达到极大值和极小值，分别约为0.074 m和-0.076 m，整体误差也在此范围内波动，15.2 s后跟踪误差为0。而PID控制器的最大横向跟踪误差达到约为0.146 m，且最终跟踪误差趋于-0.025 m。由图15 横摆角跟踪误差可以看出，MRAC-PID控制器的最大横摆角跟踪误差为-0.001～0.052 rad，控制精度高于PID控制器的0～0.118 9 rad。以PID控制器的误差为基准，基于MRAC的自适应PID控制器使横向位移误差减少了11.76%，使横摆角误差减少了55.08%。故在纵向速度为20 m/s的工况下，MRAC-PID控制器的横向位置跟踪精度同样要明显优于PID控制器。

5 总结

为解决传统控制算法所产生的横向跟踪误差大的问题，提出了一种基于MRAC 的自适应PID 控制模型，用于智能车的横向轨迹跟踪，利用MRAC 的自适应律对PID 的3 个参数进行在线仿真，结果证明本文设计的基于MRAC的自适应PID控制器在不同车速下具有良好的准确性、鲁棒性和自适应性。能够达到横向轨迹跟踪控制的目标要求，可以进一步提升轨迹跟踪控制效能，为更复杂工况下的智能车轨迹跟踪控制研究提供更精准的模型支撑。