基于Markov 模型的认知车联网频谱感知方法
殷晓虎, 谢 豪, 李加美
(西安科技大学 通信与信息工程学院, 陕西 西安 710600)
0 引言
近年来,指数式增长的汽车数量加快了智能交通系统(Intelligent Traffic System,ITS)的发展[1],车联网(Vehicle to Everything,V2X)技术旨在通过感知周围环境、采集并分析环境信息实现V2X,包括车对车(Vehicle to Vehicle,V2V)、车对人(Vehicle to People,V2P)等通信的交互式网络,在提高道路安全性和无线通信服务等方面发挥着重要作用[2-3]。虽然目前许多研究已取得突破性进展,但是随着智慧城市的快速建设,V2X 面临着新兴业务和服务数量日益激增的挑战,特别是在城市交通拥挤、交叉路口等场景,大量用户的涌入将导致V2X 频谱资源面临严重的短缺[4]。 认知无线电(Cognitive Radio,CR)技术成为解决频谱资源短缺问题的有效途径。在CR 中,次用户(Second User,SU)通过感知主用户(Primary User,PU)信号机会式地接入授权频谱,克服了传统频谱静态分配方式的局限性,提高了频谱资源利用效率,在多种无线网络领域得到了广泛应用,如认知Ad Hoc 网[5]、认知mesh 网[6]等。 因此,为了在V2X 通信中引入CR 技术,提出了认知车联网(CR-V2X)[7]。
与静态无线网络不同,CR-V2X 中车辆的移动特性会动态改变网络中的环境参数。 为了避免对PU 通信产生干扰,认知车辆应快速、准确地感知PU状态。 因此,频谱感知作为CR-V2X 的关键技术成为研究热点。 目前,频谱感知技术主要有能量检测[8]、循环平稳特征检测[9]和匹配滤波器检测[10]等。 针对CR-V2X 频谱感知方法的研究中,文献[11]对认知车载网络时空频谱感知性能进行研究,建立认知车辆的时空频谱感知模型,分析车辆移动性对时空频谱感知性能的影响。 文献[12]研究了密集场景下的频谱感知性能分析,重点对密集场景中的车辆移动性和相关性进行分析。 文献[13]研究了认知车载网络中的频谱感知性能分析,对不同的车联网衰落信道进行研究,分析影响频谱感知性能的信道因子。 文献[14]研究了一种改进能量检测方法的认知车辆移动性和PU 活动的联合影响,提出了一种改进的能量检测算法,结合移动性和PU 特性对频谱感知的性能进行研究。 考虑到PU频谱状态模型随时间周期变化具有不同统计特性的特点,本文提出了一种基于马尔可夫模型的认知车联网频谱感知方法。 根据PU 频谱的时变特性建立基于二态马尔可夫链的频谱统计模型,利用历史状态信息计算模型参数,接着对认知车辆的移动性进行分析,推导出车辆移动状态下存在频谱机会时的内部概率,最终将PU 频谱统计模型和车辆移动特性结合,并分析所提方法在不同的环境中对感知性能的影响。
1 系统模型
1.1 网络模型
网络模型如图1 所示。 网络模型为一般道路场景,PU1 和PU2 是授权用户/主用户,享有频谱使用优先级,认知车辆SU 为次用户。 当SU 存在频谱需求时通过感知周围PU 的频谱状态,机会式地接入并进行数据传输。 假设SU 与PU1 之间的初始距离为D0,SU 以速度v沿道路行驶,经过时间t之后二者之间的距离变为D。 其中,S表示SU 的感知范围,R表示PU1 的保护范围。 为了避免对PU 通信产生干扰,SU 的感知范围应大于或等于PU 的保护范围。
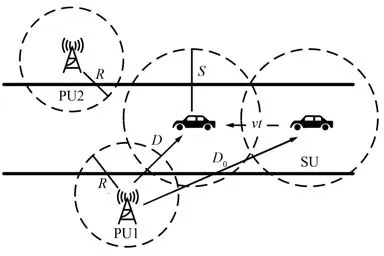
图1 网络模型Fig.1 Network Model
对于要检测到PU 频谱信息的任意SU,PU 必须在SU 的感知范围内,否则SU 无法检测到PU;另外,由于PU 具有保护范围,处于其内部的SU 不允许以任何代价访问频带[15]。 因此,只有当PU 在SU的感知范围内且SU 在PU 的保护范围外时,存在频谱共享机会。 定义事件“I”表示PU 在SU 的感知范围内且SU 在PU 的保护范围外,事件“O”表示PU位于SU 的感知范围外。
1.2 频谱感知模型
在CR-V2X 中,SU 通过频谱感知检测授权频段是否存在频谱空穴。 为了适应快速变化的车联网环境,本文采用算法复杂度较低的能量检测方法进行研究。 假设H1和H0分别表示“PU 存在(频谱繁忙)”和“PU 不存在(频谱空穴)”。 频谱感知的信号模型可以转化为以下二元假设模型[16]:
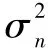
二元假设检测统计量可以表示为:
式中,λ表示能量检测方法中的判决门限;N=⎿Tsfs」表示感知周期Ts内采样的样本数量;fs为取决于信道带宽的采样频率。 根据中心极限定理,当样本数N趋于无限大时,样本检测统计量的概率密度函数为:
2 基于Markov 的PU 频谱统计模型
目前大多数研究方法基于静止的信道状态,而在实际环境中,PU 频谱活动特性随着时间周期不断变化,传统的ON/OFF 频谱模型无法满足时变的PU 信道状态。 Markov 表示一类随机过程,一个系统中t时刻的状态仅取决于前n个状态,而与未来的状态无关[17-18]。 因此,利用Markov 过程对PU 频谱活动统计建模能够更好地满足时变的PU 频谱状态。 PU 频谱统计模型可以用一个二态马尔可夫链表示,如图2 所示。 状态空间由{P0,P1}组成,P0和P1分别对应于PU 频谱状态“0”和“1”,状态转移概率分别为P00,P01,P10和P11。

图2 马尔可夫信道模型Fig.2 Markov channel model
在V2X 场景中,SU 以一定的时间周期进行频谱感知,并将感知结果上传至融合中心。 融合中心根据相应的融合准则得到最终的频谱判决结果,并保存不同时刻的频谱占用状态的统计特性,感知样本越多,得到的频谱统计信息就越充分,频谱预测的结果更精确。
假设PU 信道在t(k)时刻对历史信道信息进行统计,P0和P1的概率定义为:
式中,Ntk表示k个离散的时间样本;PU 的频谱状态转移概率表示为:
式中,j=1,2,…,k-1,其余状态之间的转移概率计算方法与式(6)相同。 因此,PU 信道状态转移概率矩阵P 可以表示为:
将式(7)计算出的频谱状态之间转换的概率作为所提频谱感知方法的先验概率。 为了控制融合中心的存储负荷,采用双端队列的形式对PU 信道状态统计信息进行存储,随着时间周期变化不断更新参数,保证了PU 频谱统计模型的实时性。
3 车辆移动性分析
与静态无线网络不同,SU 在网络中的位置随时间不断发生变化,且移动的方向和速度受道路拓扑结构和交通流量密度的约束。 因此,PU 频段能够被认知车辆检测并感知到的概率将受到PU 保护范围、SU 感知范围、移动速度和初始距离等因素的综合影响。 事件I和事件O的概率取决于移动SU 与固定PU 之间距离的分布函数。
首先,假设SU 与PU 都是静止的,二者之间的距离概率分布函数表示为:
假设网络中SU 以速度v在时间t=t′内位移的距离为vt′,因此PU 和SU 之间的最终距离为D0+vt′,D0表示t时刻PU 与SU 之间的初始距离。 因此,式(9)可以改写为:
式中,μt,σt分别表示时间均值和标准差。 为了便于计算,简单假设事件I和事件O满足互斥事件,则事件O发生的概率可以表示为:
4 漏检概率分析
漏检概率是指当PU 处于活动状态,而SU 做出“PU 空闲”判决结果的概率。 经上述分析,PU 频谱统计模型和车辆移动性会对频谱感知性能产生影响,通过推导漏检概率Pm分析频谱感知的性能。Pm的表达式为:
式中,P(Y≤λ|H1,I)和P(Y≥λ|H0,O)分别表示事件I和事件O的条件漏检概率,λ表示能量检测的判决门限,由给定的虚警概率确定。
事件I的条件漏检概率P(Y≤λ|H1,I)可以表示为:
式中,E(Y|H1,I)=,n表示自由度,和分别表示噪声方差和信号方差;Var(Y|H1,I)=2n()2。同样地,事件O的条件漏检概率P(Y≥λ|H0,O)可以表示为:
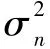
综上,通过计算事件I和事件O的条件漏检概率最终得到本文所提频谱感知方法的漏检概率,接下来分析P(I)、频谱状态转移概率等参数对感知性能的影响。
5 实验仿真与结果分析
采用Matlab 软件进行实验仿真,假设PU 与SU之间的初始距离为200 m,通过仿真产生满足泊松分布的20 000 个PU 频谱统计数据。 蒙特卡罗实验次数为10 000,其他仿真参数设置如表1 所示。
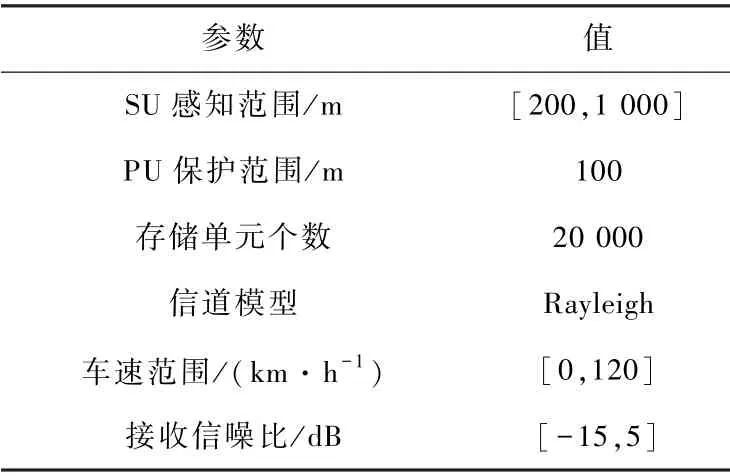
表1 主要仿真参数设置Tab.1 Main simulation parameters settings
不同SU 感知范围条件下PU 位于SU 感知范围内的概率变化曲线如图3 所示。 从图中可以看出,在速度v=20 km/h,初始距离为200 m 时,随着SU感知范围的增加,PU 位于SU 感知范围内的概率不断增加。 这表明在车辆移动速度一定的前提下,SU的感知范围越大,PU 能够被感知到的概率就越大。
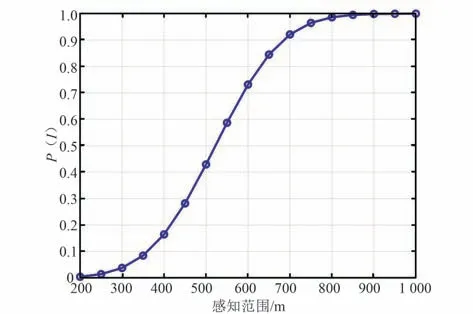
图3 PU 在SU 感知范围内的概率与不同感知范围值之间的关系Fig.3 Relationship between the probability of PU inside sensing range of SU and the values of different sensing ranges
基于Markov 模型的PU 频谱统计特性如图4 和图5 所示。 其中,m表示业务量因子,通过控制泊松分布达到率来表示实际信道的负载程度。 由图4 可以看出,PU 频谱的占用率受到时间周期内业务量因子m的影响,占用状态的概率随着业务量因子m的增大而增大,即该时间周期内的频谱机会就越少。图5 分别给出了业务量因子m为0.5 和1.5 时的频谱状态统计图,从图中可以看出,当m=0. 5 时,频谱空闲的次数达到了12 000 多,相比m= 1.5 时的频谱空闲的次数增加了约8 000。 这说明,不同时间周期的m对应的频谱状态转移概率矩阵不同。 因此,将PU 频谱占用模型的统计量作为频谱感知的先验条件,SU 可以根据感知周期内的频谱占用情况选择是否接入PU 频谱,以达到较好的通信质量。
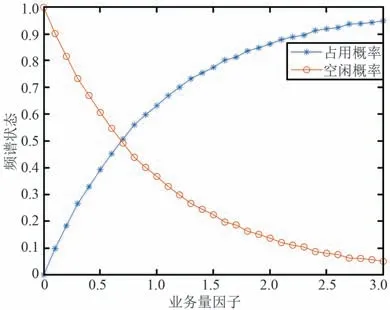
图4 业务量因子对PU 频谱状态的影响Fig.4 Influence of traffic factor on primary user spectrum status
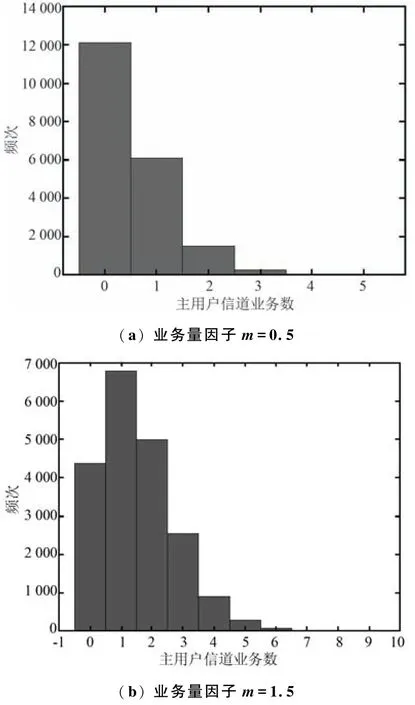
图5 基于Markov 模型的PU 频谱活动统计Fig.5 PU spectrum activity statistics based on Markov model
本文方法中得到的PU 活动统计模型与传统无PU 活动统计的传统感知方法之间的漏检概率对比如图6 所示。 由图6 可以看出,当信噪比γ为-8 dB时,2 种方法在理论和实验中的漏检概率随着虚警概率的增加快速减小,而在本文方法中,考虑了PU统计信息的先验概率,得到的漏检概率相比传统方法降低了6.5%,具有更好的感知性能。
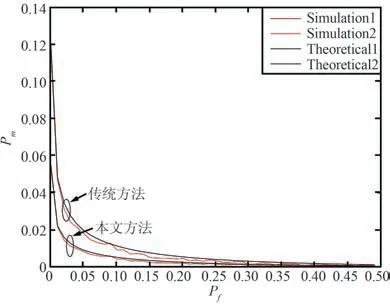
图6 本文方法与传统方法的漏检概率对比(γ=-8 dB)Fig.6 Comparison of missed detection probability between the proposed method and the traditional method(γ=-8 dB)
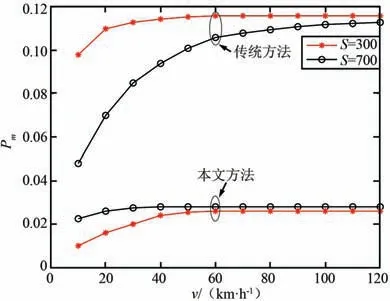
在不同感知范围条件下,当P0= 0.25 和P1=0.75 时,车辆移动速度和漏检概率之间的关系如图7 所示。 由图7 可以看出,当P0 图7 不同感知范围条件下的车辆速度和漏检概率之间的关系(P1>P0)Fig.7 Relationship between vehicle speed and missed detection probability under different sensing range conditions (P1>P0) 在不同感知范围条件下,当P0= 0.75 和P1=0.25 时,车辆移动速度和漏检概率之间的关系如图8 所示。 由图8 可以看出,当P0>P1时,随着车辆速度的增加,漏检概率在不同程度上有所提高,但是传统方法没有考虑PU 频谱状态的先验概率以及车辆移动时的内部概率,漏检概率始终大于本文方法。 图8 不同感知范围条件下的车辆速度和漏检概率之间的关系(P1 本文研究了认知V2X 中的频谱感知方法,针对认知V2X 中的PU 频谱占用模型受时间周期变化的影响,提出了基于Markov 的PU 频谱统计模型和认知车辆移动性的频谱感知方法。 根据历史统计信息计算当前PU 频谱状态的转移概率以及SU 存在频谱机会时的内部概率作为频谱感知方法的先验概率,推导出系统漏检概率的表达式。 仿真结果表明,所提方法在V2X 环境中具有更好的系统性能。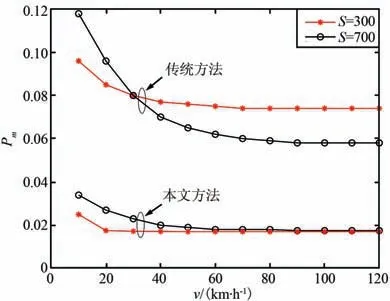
6 结束语

