广义观测相对论：时空在爱因斯坦广义相对论中为什么弯曲？(下篇)
——GOR理论与科学预言

2023-03-17 01:33阮晓钢

北京工业大学学报 2023年3期

阮晓钢

(北京工业大学信息学部，北京 100124)

7 GOR理论与行星轨道之旋进

GOR理论之引力场方程的标定和确立，意味着GOR理论的正式建立，意味着牛顿万有引力论和爱因斯坦广义相对论两大理论体系的统一. 新的理论期待新的发现和新的认识，乃至新的思想.

第6章成功地求解静态球对称引力时空之GOR场方程，由此，本章围绕爱因斯坦著名的三大预测之行星进动(行星轨道旋进)问题，测试或验证GOR理论. 我们将基于GOR理论，探究天体系统之“二体问题”(The Two-Body Problem)；运用GOR场方程和GOR运动方程，建立行星运动方程，即行星围绕恒星运行的天体“二体系统”之理论模型.

我们力求，基于PGC原理，结合PGC逻辑路线1和PGC逻辑路线2，类比爱因斯坦广义相对论之逻辑，演绎GOR理论之行星运动方程. GOR理论之行星运动模型，可与牛顿引力论之行星运动模型以及爱因斯坦广义相对论之行星运动模型对照或类比，验证或测试GOR理论及其场方程和运动方程，解析天体运动中的引力相对论性效应，特别地，解析爱因斯坦广义相对论之水星近日点反常进动预测的实质.

7.1 天体运行图像的演化

可以想象和理解，古人对于自身赖以生存的地球以及每天围绕地球东升西落的日月星辰充满好奇.

“地球”(The Globe)的概念自然是后来才有的，原本，中国人称其为“大地”(The Earth). 远古的人类很难将“大地”想象为一个球体. 人们以为：大地像一张波斯地毯，幸亏有它，我们才不至于陷入底层的地狱. 然而，无论如何，基于“眼见为实”的准则，人们会自然地认为，东升西落的日月星辰围绕大地运行，而运行轨道一定是理想的圆形.

“地球”的概念始于托勒密的“地心说”(The Geocentric Theory；见图3(a))[71]. 地心说大约形成于公元2世纪，又称“天动说”，其核心思想可归纳为：第一，大地是球体；第二，地球乃宇宙中心；第三，日月星辰皆围绕地球旋转. 自然地，地心说之日月星辰围绕地球运行的轨道也是理想的或标准的圆形.

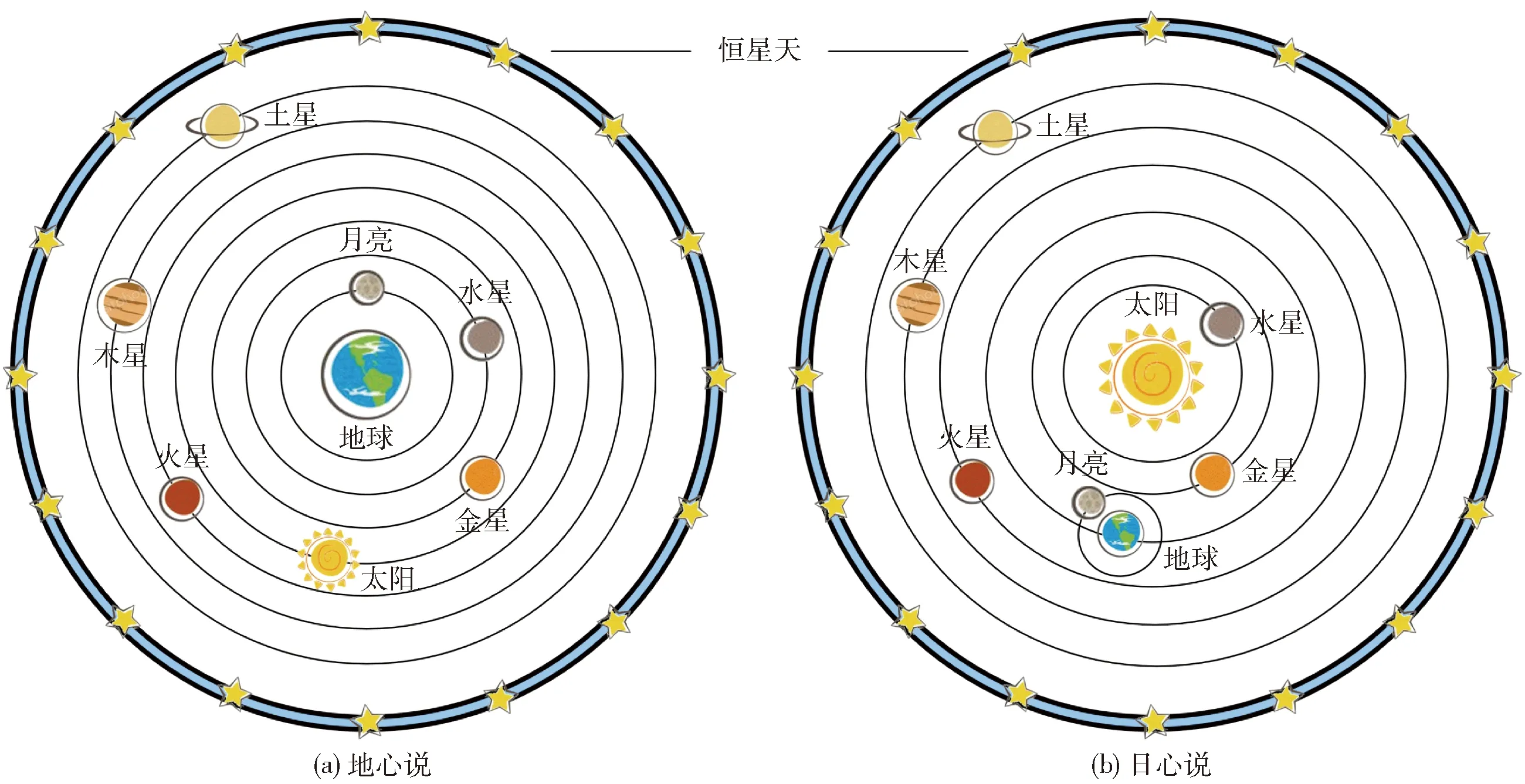
图3 地心说与日心说Fig.3 Geocentricism and heliocentric theory

公元16世纪，哥白尼创建了“日心说”(The Heliocentric Theory；见图3(b))，将宇宙的中心由地球搬到了太阳[71-72]. 日心说令人类对宇宙的认识朝向正确的方向迈进了一大步：地球绕其轴自传，月亮绕地球旋转，而地球以及其他行星则围绕太阳旋转. 然而，在哥白尼的日心说中，无论月亮绕地球运行还是行星绕太阳运行，皆因循理想的圆形轨道，并且，所有行星的运行轨道形成以太阳为中心的同心圆.

公元17世纪，开普勒基于第谷积累的天文观测资料和数据，提出了关于行星运动的三大定律，即开普勒三定律[71,73]，包括“轨道定律”，以及“面积定律”和“调和定律”(见图4(a)). 其中，“轨道定律”又称“椭圆定律”：行星围绕太阳运行的轨道是椭圆，而太阳位于椭圆的一个焦点上. 开普勒轨道定律表明，星体运行轨道未必是理想的或标准的圆形. 然而，特别值得注意，开普勒的行星椭圆轨道是封闭的或闭合的，其中，行星之近恒星点不存在进动，或者说，行星轨道不存在旋进.

图4 天体运行轨道Fig.4 Orbits of celestial bodies

开普勒三定理之后，牛顿三定律以及牛顿万有引力定律相继诞生[53]. 基于牛顿定律，开普勒三定律皆可从理论上导出；人类的物理学开始由唯象物理学上升至理论物理学. 牛顿万有引力论能预测更为广义的圆锥曲线轨道：物质体系在引力场中运动，其运行轨迹可以是圆、椭圆、抛物线，以及双曲线，皆为标准的圆锥曲线. 将牛顿万有引力定律应用于天体系统之“二体问题”，可以建立行星围绕恒星运行的理论模型，计算行星运行轨道. 牛顿之行星运动方程支持开普勒之“轨道定律”：行星轨道乃封闭的或闭合的椭圆，不存在进动或旋进.

然而，通过实际的天文观测，天文学家发现，行星之运行轨道并非闭合的椭圆，其近恒星点总是不断地进动(见图4(b)). 水星近日点的进动尤为突出，其轨道旋进率为每100年5 600.73角秒[55].

物理学任何理论都只是物理现实的某种理想化模型. 行星和恒星之“二体系统”本身是一种极度理想化的体系，并且，还常常被进一步理想化作“单体问题”(The One-Body Problem)，“二体系统”约化为“单体系统”(The One-Body Systme)：行星围绕着静止的恒星运行. 如此，相应的理想化条件包括：引力辐射速度无穷；恒星静止，行星围绕恒星运行；恒星和行星皆质点，无论视其为“单体”还是“双体”，皆孤立体系；观测者本应基于恒星视角，理论上，应相对于恒星静止且处于零势位；行星运动信息的传递无须时间. 而天体系统之实际情形是：引力辐射速度是有限的；恒星和行星通过引力，相互作用，相对运动；恒星和行星皆非质点，其物质分布非均匀、非对称、非静态；恒星和行星处于无数星体包围中，非孤立体系；观测者一般位于地球，处于太阳和地球之引力场中，相对于太阳和被观测行星运动；行星之运动信息的传递速度有限，跨越空间需要时间.

因此，可以想象，我们所观测的天象，包括月球围绕地球运行，地球以及水星和火星等行星围绕太阳运行，其实际运行轨迹必定不是理想化的闭合的椭圆轨道. 客观物理世界，其行星轨道呈现进动或旋进是自然而合理的，甚至，是必然的. 相反地，我们很难想象，天体能周而复始地沿着同一闭合椭圆轨道运行而没有漂移. 实际上，就天文观测数据和实际观测结论而言，客观真实的天体系统，其符合理论模型的程度，已经远远地超越了我们的想象或预期. 就水星而言，其围绕着太阳每公转1周仅仅旋进了大约13.5角秒——千分之3.75度. 可见，牛顿之天体“二体系统”理论模型已经相当完美.

水星，作为太阳系距离太阳最近的行星，其运行轨道的旋进最为突出. 物理学家们针对水星- 太阳“二体系统”的非理想化因素，进行了一番修正性的计算(所采用的仍然是牛顿理论)，扣除坐标系之“岁差”的影响(约占90%)，以及其他行星(特别是金星和地球以及木星)之“摄动”的影响(约占10%)，共计5 557.62角秒；最后，还剩下5 600.73-5 557.62=43.11角秒找不到归宿. 其实，每100年旋进43.11角秒可谓“小量”，太阳引力之局域性、太阳不规则的形态、太阳的自旋等，都可能加剧水星进动.

1915年，爱因斯坦继1905年建立狭义相对论[14]之后，建立了广义相对论[15]. 爱因斯坦将其广义相对论应用于天体之“二体问题”，建立了爱因斯坦广义相对论之行星运动方程，其中，包含着牛顿之行星运动方程所不具有的信息：行星轨道旋进项. 神奇出现了：爱因斯坦之行星运动方程用于计算水星围绕太阳运行，所得水星近日点之进动率为每100年43.03角秒，与实际观测值5 600.73角秒中找不到归宿的43.11角秒极度吻合. 尽管有不少物理学家认为，其中尚存疑点，不宜下最终结论[74]，而物理学界则普遍认为这一计算结论是对爱因斯坦广义相对论的支持.

其中的问题是：无论43.11角秒或43.03角秒，都只是水星近日点进动之实际观测值5 600.73角秒中极小的部分，不足0.8%；那么，为什么爱因斯坦广义相对论只预测水星实际进动5 600.73角秒中的0.8%，却不能预测另外的99.2%呢？另外，还有一个问题：造成水星进动的因素很多，物理学家们为什么不能采用爱因斯坦广义相对论，扣除非理想化因素对水星进动造成的影响，验证其是否确实为5 557.62角秒呢？

归纳并梳理一下：第一，水星轨道旋进率实际达到了每100年5 600.73角秒；第二，牛顿之行星运动方程对水星轨道旋进率的预测为0；第三，爱因斯坦广义相对论对水星轨道旋进率的预测为每100年43.03角秒，与实际的5 600.73角秒相去甚远，无可比性.

实际上，爱因斯坦广义相对论之行星运动方程隐喻了牛顿万有引力论之行星运动方程所设定或隐喻的几乎所有理想化条件，包括第3章之3.1指出的：引力辐射速度无穷. 唯一的不同是，爱因斯坦之理论模型隐喻着“观测局域性条件”：行星的运动信息需要通过光来传递. 正如OR和GOR理论所阐明的，爱因斯坦的理论是光学观测理论，归属光学代理OA(c)，其信息波速度乃光速c，是有限的，自然地，存在观测局域性(c<∞).

无论爱因斯坦之行星运动模型，还是牛顿之行星运动模型，都没有关行星近恒星点进动或行星轨道旋进的任何先验信息，比如，坐标系之“岁差”和其他行星之“摄动”，以及太阳的非理想化形态和非静态特性. 与牛顿之行星运动方程一样，爱因斯坦之行星运动方程也没有关于水星那5 557.62角秒进动值的先验信息，自然地，不可能对其做出相应的预测.

GOR理论将会阐明：爱因斯坦之行星运动方程所预测的水星轨道旋进率(每100年43.03角秒)，并不代表水星实际的进动，而是一种由光学代理OA(c)之观测局域性(c<∞)所导致的观测效应.

特别需要指出，5 600.73角秒的水星进动数据源于光学观测代理OA(c). 假定，作为观测代理之观测效应的行星轨道旋进，能反映并记录在实际的天文观测数据中，那么，爱因斯坦广义相对论所预测的水星轨道每100年旋进43.03角秒，确实可以用于解释实际天文观测数据那5 600.73角秒中还未找到归宿的43.11角秒. 如此，这将意味着对爱因斯坦广义相对论的支持，理所当然地，更是对GOR理论的支持.

就水星近日点进动或水星轨道旋进而言，实际的天文观测似乎更倾向于支持爱因斯坦广义相对论，而非牛顿万有引力论. 这并不令人感到意外，也并不意味着爱因斯坦广义相对论比牛顿万有引力论更正确. 一直以来，我们的天文学，包括射电天文学，皆光学代理OA(c)之天文学，其信息波速度皆光速c，自然地，其天文观测更合乎归属光学观测代理OA(c)的爱因斯坦广义相对论.

本章将基于GOR理论，建立新的天体之“二体系统”理论模型，导出GOR行星运动方程. 基于PGC对应原理，GOR行星运动方程必定与爱因斯坦行星运动方程同构一致，自然地，也会包含行星轨道旋进项，进而，对行星(包括水星)公转轨道旋进率做出预测. 可以预见，类似于爱因斯坦广义相对论之行星运动方程依赖于光学代理OA(c)和光速c，GOR行星运动方程必定依赖于一般观测代理OA(η)及其信息波速度η：同一行星，不同观测代理OA(η)，将会呈现不同的进动或轨道旋进. 据此，我们可以做出判断：爱因斯坦广义相对论所预测的水星轨道旋进率，乃至GOR理论可能预测的行星轨道旋进率，并不代表水星或行星真实的进动，而是一种表观现象.

7.2 牛顿之行星运动方程

开普勒之“椭圆轨道”定律[71]表明，行星沿椭圆轨道围绕恒星运行，而恒星则位于椭圆的一个焦点之上. 这一定律主要基于第谷之火星观测数据[73].

开普勒三定律的建立，极大地推动了人类对天体运行规律的认识和对天体运动之推动力的探索. 由此，伽利略提出了“有心力”(central force)的概念；而牛顿则建立了万有引力定律[53]. 如此，行星围绕恒星运行的轨道便可从理论上导出. 然而，牛顿万有引力定律所导出的行星运动方程是更具有普遍意义的圆锥曲线，椭圆轨道只是其中的一种形式.

牛顿之行星运动方程自然基于经典力学和牛顿定律，包括牛顿第二定律和牛顿万有引力定律. 牛顿之行星运动方程，属普通物理教科书的范畴，然而，作为GOR理论之行星运动方程的一个特例，对于我们认识和理解GOR理论，具有重要意义.

7.2.1 牛顿天体“二体问题”

无论牛顿之行星运动方程，还是爱因斯坦之行星运动方程，都属天体之“二体问题”，乃天体“二体系统”之理论模型，是极度理想化的，可如下描述.

天体“二体系统”：(M,m)，天体M和天体m通过万有引力相互作用，m在M之引力场中运动.

牛顿“二体系统”之理想化条件：牛顿之天体“二体系统”(M,m)设立了或隐喻着理想化条件——超距引力作用，即引力乃超距作用，辐射速度无穷.

孤立质点体系：(M,m)为一孤立体系，天体M和天体m皆可视为质点，M静止，m在M之引力场中运动，不受M和m之外的物质或能量影响.

理想观测代理：牛顿之观测代理OA(η)乃理想代理OA∞，其信息波速度η乃理想化的无穷大(η→∞)，天体m之运动信息的传递无须时间.

理想观测者：观测者O借助理想代理OA∞，基于M之视角观测m之运动，理论上，O相对于M静止且处于引力势之零势位.

天体“二体系统”之形式化坐标：如图5所示，选择笛卡儿3d坐标(x,y,z)及其对应的球坐标(r,θ,φ)表达天体之“二体系统”(M,m)的3d空间(见图5(a)；式(6.6))；设定大质量天体M为坐标原点O，设想小质量天体m在X-Y(θ=π/2)平面内运动(见图5(b)).

实际上，牛顿以及爱因斯坦研究的天体“二体问题”，可进一步理想化并约化为“单体问题”，乃“单体系统”之理论模型，其中，只探索行星运动，而恒星是静止的，即从恒星的视角看行星的运动.

7.2.2 万有引力论与天体“二体系统”

理想化的天体之“二体系统”(M,m)中，质点M和质点m通过万有引力相互作用；万有引力乃“有心力”，质点m之受力作用线始终连接M之质心.如图5(a)所示，以F(r)代表m所受之有心力；F(r)是r的函数：F(r)=Frr/r.F(r)属万有引力，始终指向质点M(坐标原点O)，故有：Fr<0.

图5 天体“二体系统”之形式化坐标Fig.5 Formal coordinates of Two Celestial Bodies

牛顿第二定律与行星运动——

根据牛顿第二定律：

(7.1)

式中：r乃M指向m的矢径；F(r)为M对m的引力(有心力)；m为小天体之质量(≪M).

在直角坐标系(x,y,z)中：

(7.2)

在对应的球坐标系(r,θ,φ)中：

(7.3)

式中：hK=rv=L/m乃一常量，称“速度矩”；L=rmv即角动量，或称“动量矩”；理想代理OA∞中，t=τ.

式(7.3)证明了开普勒三定律之“面积定律”(见图1(c))：行星矢径r单位时间内扫过的面积相等；同时，证明了角动量守恒定律：L=mr2dφ/dt乃一常量.

作为有心力，万有引力F(r)始终指向力心M；依经典力学，受力质点m始终保持在X-Y(θ=π/2)平面.

比耐方程——

万有引力F(r)乃保守力，基于机械能守恒定律，运用式(7.3)可导出比耐公式

(7.4)

牛顿万有引力定律与行星运动方程——

将牛顿万有引力定律代入比耐公式(7.4)，即可得到基于牛顿万有引力论的天体m之运动方程

(7.5)

式中：G乃万有引力常数；M为大天体之质量(≫m).

行星运行轨道的形式——

解微分方程(7.5)，可得

(7.6)

此即标准的“圆锥曲线”方程，式中：天体M位于圆锥曲线的一个焦点；e为天体m之轨道偏心率；CS和φ0则为积分常数.

调整时间零点，或者，绕Z轴转动X-Y平面，可将天体m之轨道初始角φ0设定为特定值，或置φ0=0；而CS则取决于m之初始角动量L及其机械能E.

天体“二体系统”(M,m)中，天体m之轨道偏心率e=CSp依赖于引力常量数G和引力场源M，以及运动天体m之初始机械能E和角动量L.

依照经典天体力学之公式

(7.7)

式中：总机械能E=K+V，即天体m之动能K与势能V的和；角动量L=mrv，v为天体m之运动速度，r为天体m之轨道矢径，而m又代表天体m之质量.

由式(7.7)可知，天体“二体系统”模型(M,m)(式(7.5))中，天体m之运行轨道的偏心率e乃一常数.

偏心率e决定了天体m运行轨道的形式：

e=0，m之轨道即圆；

1>e>0，m之轨道即椭圆；

e=1，m之轨道即抛物线；

e>1，m之轨道即双曲线.

束缚于恒星的行星，其轨道自然只能是椭圆.因此，其运行轨道偏心率e必定为：1>e>0.以水星为例，其绕日运行轨道之偏心率e=0.205 6；而地球轨道之偏心率则只有0.016 7，更接近于圆.

牛顿之行星运动方程(7.5)及其解(式(7.6))证明了针对行星的开普勒第一定律：“椭圆定律”.

7.2.3 牛顿之行星运动方程与行星轨道旋进

设行星m之轨道初始角φ0=0，则牛顿行星运动方程(7.5)之解可写作

(7.8)

式中万有引力常数G和恒星质量M，以及行星m之速度矩hK和轨道偏心率e，皆常数.

对于行星轨道近日点，应成立：du/dφ=0.

设行星m运行一周之“进动”为Δφ；令k=1，即行星m围绕恒星M运行一周(见图4(b)：行星由近恒星点P出发运行至下一近恒星点P′)，其扫过的角度应为φ=2π+Δφ；代入式(7.10)可知：Δφ=0.

可见，基于牛顿行星运动方程(7.5)(7.6)，行星m之运行轨道不存在进动或旋进.

实际上，牛顿之行星运动方程(7.5)(7.6)意味着，行星围绕恒星运行的轨道，乃理想的和标准的椭圆，是闭合的，不存在轨道旋进，自然地，不能预测行星近恒星点之进动或行星轨道之旋进.

为什么牛顿之天体“二体系统”理论模型没能预测行星近恒星点之进动或行星轨道之旋进呢？

在太阳系中，水星运行轨道的旋进尤为突出.或许，正是因为水星距离太阳最近，相应地，水星- 太阳之“二体系统”的非理想化因素更为突出.天文观测表明，实际的水星轨道每100年旋进了 5 600.73角秒.考虑非理想化因素后的修正计算显示，其中，5 557.62角秒源于坐标系之“岁差”以及其他行星(特别是金星和地球以及木星)之“摄动”.然而，有关“岁差”和“摄动”的先验知识或先验信息并不包含在牛顿理想化的天体“二体问题”之中.因而，牛顿之行星运动方程(7.5)(7.6)不能预测水星这5 557.62角秒的进动.而剩余的43.11角秒，或许属于观测残差，或许应归咎于其他不明因素，有待进一步探究.

那么，爱因斯坦广义相对论之行星运动方程预测水星轨道每100年旋进43.03角秒又意味着什么呢？

实际上，就理想化的天体“二体问题”而言，其中，并无任何有关水星或行星轨道旋进的先验知识或信息.因此，无论基于牛顿万有引力论或爱因斯坦广义相对论，乃至GOR理论，都不可能通过如此理想化的天体“二体系统”理论模型，预测诸如“岁差”和“摄动”等实际因素所导致的行星轨道旋进.

重温牛顿之行星运动方程，并与爱因斯坦之行星运动方程和GOR行星运动方程类比，将有助于我们认识和理解爱因斯坦广义相对论及其行星运动方程，进而，认识和理解GOR理论及其GOR行星运动方程.

7.3 爱因斯坦之行星运动方程

牛顿之行星运动方程是基于经典力学和牛顿定律导出的，是牛顿万有引力定律的产物；而爱因斯坦之行星运动方程则是爱因斯坦广义相对论的产物.然而，它们都属于天体之“二体问题”，乃天体“二体系统”之理论模型，描述天体在引力场中的运动.

基于爱因斯坦广义相对论，可建立针对天体“二体问题”的爱因斯坦场方程，解之可得天体“二体系统”之时空度规，代入广义相对论之运动方程，即可建立爱因斯坦之行星运动方程.如同牛顿之行星运动方程，爱因斯坦之行星运动方程也是GOR行星运动方程的一个特例，其逻辑演绎的思想和方法，将作为GOR理论之天体“二体系统”理论模型的参照.

7.3.1 爱因斯坦天体“二体问题”

与牛顿之天体“二体系统”理论模型一样，爱因斯坦之天体“二体系统”理论模型也包含着理想化条件，可如下描述.

天体“二体系统”：(M,m)，天体M和天体m通过万有引力相互作用，m在M之引力场中运动.

爱因斯坦之“二体系统”的理想化条件：爱因斯坦之天体“二体问题”及其“二体系统”(M,m)设立或隐喻着如下理想化条件.

超距引力作用：引力乃超距作用，辐射速度无穷.

孤立质点体系：(M,m)为一孤立体系，天体M和天体m皆可视为质点，M静止，m在M之引力场中运动，不受M和m之外的物质或能量影响.

上述理想化条件，与牛顿之天体“二体问题”中的“超距引力作用”假设和“孤立质点体系”假设相同.然而，爱因斯坦之天体“二体问题”并不包含“理想观测代理”和“理想观测者”之假设，取而代之的是“光学观测代理”和“光学观测者”条件.

光学观测代理与光学观测条件：爱因斯坦光之天体“二体问题”及其“二体系统”(M,m)中，观测代理是实际的和非理想化的，乃特定之观测代理，隐喻着如下观测条件.

光学观测代理：爱因斯坦之观测代理OA(η)乃光学代理OA(c)，其信息波速度η即光速c，天体m之运动信息的传递需要时间.

光学观测者：观测者O借助光学代理OA(c)，基于M之视角观测m之运动，理论上，O相对于M静止且处于引力势之零势位.

牛顿没能意识到，自己的理论隐喻着“理想代理OA∞”；同样，爱因斯坦也没能意识到，自己的理论隐喻着“光学代理OA(c)”.OR和GOR理论已经阐明，爱因斯坦相对论，包括狭义相对论和广义相对论，乃光学观测理论.自然地，爱因斯坦之行星运动方程中为观测者传递行星运动信息的观测代理，不再是牛顿万有引力论之理想代理OA∞，而是光学代理OA(c)，其中，存在着观测局域性(c<∞).

这正是牛顿之天体“二体系统”理论模型与爱因斯坦之天体“二体系统”理论模型的根本区别.

光子- 太阳“二体系统”之形式化坐标：爱因斯坦之天体“二体问题”及其“二体系统”同样采用如图5所示的形式化坐标体系：选择笛卡儿3d坐标(x,y,z)及其对应的球坐标(r,θ,φ)描述天体之“二体系统”(M,m)的3d空间(见图5(a)；式(6.6))；质点M(恒星)设定为坐标原点O，设想质点m(行星)在X-Y(θ=π/2)平面内运动(见图5(b)).

与牛顿之天体“二体问题”一样，爱因斯坦研究的天体“二体问题”也可进一步理想化或约化为“单体问题”和“单体系统”之理论模型.

7.3.2 广义相对论与天体“二体系统”

广义相对论建立之后，爱因斯坦即将其应用于天体之“二体问题”，基于其场方程的弱场近似解，建立了行星运动方程，并且，计算出水星轨道旋进率为每100年43.03角秒[15].之后，Schwarzschild在第一次世界大战前线的战壕里得到了静态球对称引力场之爱因斯坦场方程的精确解[57].基于Schwarzschild精确解，可以建立起更为精确的天体之“二体系统”理论模型，获得有关行星运动更多更准确的信息.

针对天体之“二体问题”，基于爱因斯坦广义相对论，将Schwarzschild精确解(见第6章之式(6.7)(6.8))代入广义相对论之线元方程和广义相对论之运动方程(“短程线”)，即可构建行星运动方程.

Schwarzschild线元公式——

如式(6.7)(6.8)所示，Schwarzschild精确解乃球坐标(r,θ,φ)之时空度规gμν=gμν(r,θ)：

(7.9)

于是，Schwarzschild线元公式可表述为

ds2=g00dx0dx0+g11dx1dx1+g22dx2dx2+g33dx3dx3=
eξc2dt2-eζdr2-r2dθ2-r2sin2θdφ2
(x0=ct,x1=r,x2=θ,x3=φ;μ=0,1,2,3)

(7.10)

其中，r=0(代表质心)以及r=2GM/c2(代表M球面)均为Schwarzschild线元公式之奇点.

行星运动之“短程线”——

将Schwarzschild精确解代入爱因斯坦广义相对论之运动方程(“短程线”方程)，即可获得天体“二体系统”之运动方程，或行星运动之“短程线”：

(7.11)

式中：t为“观测时间”(爱因斯坦称其“坐标时间”)；τ为“固有时间”(爱因斯坦称其“标准时间”).

式(7.11)共有4个方程式(μ=0,1,2,3)：1)t=t(τ)，2)r=r(τ)，3)θ=θ(τ)，以及4)φ=φ(τ).剖析其中各方程式，有助于我们对爱因斯坦广义相对论之天体“二体系统”理论模型的理解和对光学代理OA(c)之行星运行轨道的认识，同时，为GOR理论之天体“二体系统”理论模型的建立提供类比和借鉴.

方程式t=t(τ)与时空变换因子——

基于Schwarzschild度规gμν=gμν(r,θ)[74]可得

(7.12)

令μ=0，则xμ=x0=ct；由式(7.11)可知

(7.13)

对照式(7.11)与式(7.12)可得t之二阶微分方程式

(7.14)

对t之方程式(7.14)进行一次积分得

(7.15)

式中：Ct为常数；而γ=dt/dτ正是爱因斯坦广义相对论中的时空变换因子.

依照爱因斯坦广义相对论的概念，t之微分方程(7.14)所描述的是“坐标时间”t与“标准时间”τ的关系，意味着运动物体(行星)m之“坐标时间”t不同于“标准时间”τ.实际上，t之微分方程式(7.14)具有更为深刻的含义：爱因斯坦广义相对论之观测代理乃光学代理OA(c)，而光学代理OA(c)之“观测时间”t不同于客观真实的“固有时间”(原时)τ.

方程式θ=θ(τ)与行星轨道平面——

基于Schwarzschild度规gμν=gμν(r,θ)[74]可得

(7.16)

令μ=2，则xμ=x2=θ；由式(7.11)可知

(7.17)

对照式(7.11)与式(7.16)可得θ之二阶微分方程式

(7.18)

不失一般性，假定某个初始时刻t=0，质点(行星)m运行在X-Y(θ=π/2)平面内，则

(7.19)

θ之方程式(7.18)及式(7.19)意味着，在爱因斯坦广义相对论之“二体系统”理论模型式(7.11)中，质点(行星)m的轨道平面是恒定不变的.这与开普勒轨道定律以及牛顿之行星运动方程的结论是一致的.

方程式φ=φ(τ)与开普勒面积定律——

基于Schwarzschild度规gμν=gμν(r,θ)[74]可得

(7.20)

令μ=3，则xμ=x3=φ；由式(7.11)可知

(7.21)

对照式(7.11)与式(7.20)可得φ之二阶微分方程式

(7.22)

已知行星轨道平面是恒定的，不失一般性，可设质点(行星)m运行于X-Y(θ=π/2)平面，则φ之方程式(7.22)可写作

(7.23)

对φ之方程式(7.23)进行一次积分得

(7.24)

式中行星之速度矩hK=L/m为常数或不变量，自然地，行星角动量L=mhK也是常量或不变量.

这正是开普勒三定律之“面积定律”(见图4(a)；式(7.3))：行星矢径r单位时间内扫过的面积相等.本质上，式(7.24)即角动量守恒定律：L=rmv是不变的.(特别注意，这里要求行星质量m为引力质量，或者说，为行星之“固有质量”，而非“相对论性质量”.)

特别需要指出：牛顿之行星运动方程(7.3,5)中，开普勒三定律之“面积定律”的表述为r2dφ/dt≡hK，其中，似乎时间t是观测时间或坐标时间，而非固有时间或标准时间τ.有物理学家认为，开普勒和牛顿之经典理论中速度矩常数hK≡r2dφ/dt与爱因斯坦广义相对中速度矩常数hK≡r2dφ/dτ存在着“些微差异”[74].然而，实际上，开普勒定律与牛顿定律一样，属理想观测代理OA∞；根据第4章“伽利略时空定理”之引理A，OA∞之“观测时间”t即“固有时间”τ：dt=dτ.因此，无论是开普勒表述的“面积定律”，还是经典理论导出的“面积定律”r2dφ/dt≡hK(式(7.3,5))或爱因斯坦广义相对论导出的“面积定律”r2dφ/dτ≡hK(式(7.24))，其表述是相同的或等价的，并且，是行星运动之客观规律的表述，不含观测效应.

方程式r=r(τ)与行星轨道方程——

基于Schwarzschild度规gμν=gμν(r,θ)[74]可得

(7.25)

令μ=1，则xμ=x1=r；由式(7.11)可知

(7.26)

对照式(7.11)与式(7.25)可得r之二阶微分方程式

(7.27)

利用Schwarzschild线元公式(7.10)可得

(7.28)

于是，式(7.27)可重写作

(7.29)

已知行星轨道平面是恒定的，不失一般性，可设质点(行星)m运行在X-Y(θ=π/2)平面，则

(7.30)

这便是基于爱因斯坦广义相对论建立的天体之“二体系统”理论模型——爱因斯坦之行星轨道方程，是行星轨道矢径r和行星轨道角度φ关于标准时间τ的二阶非线性微分方程式，其中，设定的行星轨道平面为：X-Y(θ=π/2).

7.3.3 爱因斯坦之行星运动方程的比耐形式

通常，物体之3d空间运动轨迹可由球坐标方程组表述：1)r=r(t)，2)θ=θ(t)，3)φ=φ(t).然而，对于有心力(如万有引力)，物体运动平面恒定，运动方程可约化为：r=r(t)和φ=φ(t)，并且，角动量L=hKm守恒，因而，φ关于时间t的微分可通过dφ/dt=hK/r2消除，进而，得到行星轨道矢径r之倒数u(=1/r)关于行星轨道角度φ的二阶微分方程：d2r/dφ2=u(φ)，其经典的形式如比耐方程(式(7.4)).

利用式(7.24)，式(7.30)可写作

(7.31)

因循比耐方程式(7.4)的逻辑思想和逻辑方法，令u=1/r，则dφ/dτ=hK/r2=hKu2，且

(7.32)

代入式(7.31)即得

(7.33)

这便是比耐形式的爱因斯坦之行星运动方程，乃u(=1/r)关于φ的二阶非线性微分方程，其中，既包含了行星轨道之矢径r的信息，也包含着行星轨道之角度φ的信息.

对照牛顿之行星运动方程(7.5)可知，爱因斯坦之行星运动方程(7.33)右端多出了一项：3GM/(c2r2).这意味着，爱因斯坦方程(7.33)：第一，乃非线性微分方程；第二，乃非标准圆锥曲线方程，其中的3GM/(c2r2)可谓“行星轨道旋进项”——行星轨道因而不再是标准的或封闭的椭圆，会呈现出微微的旋进.

7.3.4 爱因斯坦之行星运动方程与行星轨道旋进

基于爱因斯坦广义相对论之天体“二体系统”理论模型，求解爱因斯坦之行星运动方程(7.33)，可计算并预测行星轨道的旋进.

将式(7.6)代入式(7.33)，则

(7.34)

解之可得

(7.35)

对于行星轨道近日点，应成立：du/dφ=0.因此，对式(7.34)两端求关于φ的导数可得

(7.36)

若不计φcosφ，则

(7.37)

即sinφ=0，其解为φ=arcsinφ=2kπ(k=0,1,2,…).这意味着，若不计φcosφ，则行星轨道将与牛顿之行星运动方程一样，为一封闭的椭圆，不存在旋进.

考虑φcosφ：设行星运行一周之“进动”为Δφ，乃一小量(Δφ≪1)；令k=1，即行星围绕恒星运行一周(见图4(b)：行星由近恒星点P出发运行至下一近恒星点P′)，其扫过的角度应为φ=2π+Δφ.代入式(7.36)，并忽略高阶小量，则

(7.38)

根据国际标准组织之推荐值可知：

光速c=2.997 924 5×108m/s；

万有引力常数G=6.674 30×10-11m3/(kg·s2)；

太阳质量M=1.988 47×1030kg；

水星质量m=3.301 1×1023kg；

水星轨道角动量L=8.982 5×1038kg·m2/s；

水星速度矩常数hK=L/m=2.721 1×1015m2/s.

由式(7.38)可计算水星公转一周之轨道旋进量：

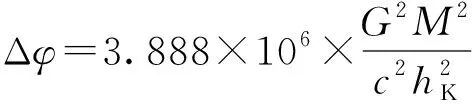
(7.39)

水星公转周期TM=87.961 d；而地球公转周期TE=365.242 19 d.如此，每100个地球年，水星轨道将会旋进φ=100×Δφ×TE/TM=42.77角秒.

爱因斯坦当时基于其广义相对论计算得出的水星近日点进动值为43.03角秒，恰与水星“找不到归宿”的43.11角秒高度吻合.爱因斯坦在给友人的信中说：“……方程给出了水星近日点的正确数字，你能想象，我有多高兴！好些天，我高兴得不能自已.”

然而，天文观测显示，水星实际的轨道旋进率为每100年5 600.73角秒；而爱因斯坦广义相对论所能预测的仅约43角秒，与实际情形相去甚远，不足1%.因而，此43角秒远不能用于认定爱因斯坦广义相对论能正确预测水星近日点之进动.

7.3.5 爱因斯坦之43.03角秒意味着什么？

关于爱因斯坦广义相对论对于水星近日点进动或水星轨道旋进的预测，有2个问题值得深思：

第一，既然爱因斯坦广义相对论能预测水星实际5 600.73角秒进动中“找不到归宿”的43.11角秒，那么，爱因斯坦为什么不能预测其余的5 557.62角秒呢？

第二，已知水星之实际的5 600.73角秒进动中有5 557.62角秒乃坐标系之“岁差”以及其他行星之“摄动”所致，那么，爱因斯坦广义相对论所预测的43.03角秒水星进动又是什么因素导致的呢？

首先，无论牛顿之行星运动方程，或爱因斯坦之行星运动方程，都无法预测坐标系之“岁差”以及其他行星之“摄动”所导致的水星5 557.62角秒之进动，因为，在牛顿和爱因斯坦的天体“二体系统”理论模型之前提条件中，不具有关于坐标系之“岁差”以及其他行星之“摄动”的先验信息或先验知识.

其次，爱因斯坦之行星运动方程中，行星轨道存在每100年约43角秒的旋进；而牛顿之行星运动方程中，行星轨道没有旋进.这一差别只能源于牛顿之天体“二体问题”与爱因斯坦之天体“二体问题”前提条件的不同.实际上，牛顿二体问题和爱因斯坦二体问题的差别仅在于观测代理：牛顿之观测代理是理想化的，即理想代理OA∞，不存在观测局域性，行星运动信息的传递不需要时间；而爱因斯坦之观测代理乃光学代理OA(c)，存在观测局域性(c<∞)，行星运动信息的传递依赖于光，需要时间.正如式(7.33)和式(7.38)所示，爱因斯坦之行星运动方程中的“行星轨道旋进项”3GM/(c2r2)，以及爱因斯坦之行星运动方程所预测的行星进动量Δφ=Δφ(c)，皆依赖于光速c.

或许，爱因斯坦广义相对论所预测的水星43.03角秒进动，正是光学天文观测数据中，水星5 600.73角秒进动中“找不到归宿”的43.11角秒.如此，与其说那是对爱因斯坦广义相对论的支持，不如说是对GOR理论的支持：爱因斯坦那43.03角秒，正是光学代理OA(c)之观测局域性(c<∞)导致的表观现象.

GOR理论将会告诉我们，爱因斯坦之行星运动方程中，行星近恒星点之进动或行星轨道之旋进并非行星真实的进动或轨道旋进，而是观测代理OA(η)之观测局域性(η<∞)所致的观测效应或表观现象.

7.4 GOR行星运动方程

GOR行星运动方程，与牛顿之行星运动方程和爱因斯坦之行星运动方程一样，归属天体“二体问题”，乃天体“二体系统”之理论模型.

GOR理论之天体“二体系统”理论模型，将因循PGC对应原理，基于GOR理论之引力场方程和运动方程导出.自然地，在PGC对应原理的意义上，GOR行星运动方程与爱因斯坦之行星运动方程具有严格的同构一致性对应关系.然而，多少有些令人意外的是，GOR行星运动方程与来自经典力学的牛顿之行星运动方程同样具有严格的同构一致性对应关系.

7.4.1 GOR天体“二体问题”

同属天体之“二体问题”，或者，更严格地，可视其为“单体问题”，GOR行星运动方程，与牛顿和爱因斯坦的行星运动方程一样，也包含着理想化条件，不具有任何可供预测行星近恒星点之进动或行星轨道之旋进的先验信息或先验知识，比如，坐标系之“岁差”或其他行星之“摄动”.

与牛顿和爱因斯坦之天体“二体系统”理论模型一样，GOR天体“二体系统”理论模型也包含着理想化条件，可如下描述.

天体“二体系统”：(M,m)，天体M和天体m通过万有引力相互作用，m在M之引力场中运动.

GOR天体“二体系统”之理想化条件：GOR理论为天体“二体问题”及其“二体系统”(M,m)设立了如下理想化条件.

超距引力作用：引力乃超距作用，辐射速度无穷.

孤立质点体系：(M,m)为一孤立体系，天体M和天体m皆可视为质点，M静止，m在M之引力场中运动，不受M和m之外的物质或能量影响.

上述理想化条件，与牛顿和爱因斯坦的天体“二体问题”中的“超距引力作用”假设和“孤立质点体系”假设相同.所不同的是，GOR天体“二体问题”中，观测代理为一般观测代理.

一般观测代理与一般观测条件：GOR天体“二体问题”及其“二体系统”(M,m)中，观测代理即GOR理论之观测代理，为一般代理，而非特定代理.

一般观测代理：GOR天体“二体系统”(M,m)之观测代理乃一般观测代理OA(η)，理论上，一切物质运动形式皆可为观测媒介，其信息波速度η可为任意物质运动速度，大于或等于作为被观测对象的天体m之运动速度.

一般观测者：观测者O可借助于一般代理OA(η)，基于M的视角观测m之运动，理论上，O相对于M静止且处于引力势之零势位.

GOR理论及其天体“二体系统”的观测代理假设是合理的：人类感知客观世界的媒介未必只能是光.

天体“二体系统”之形式化坐标：GOR理论之天体“二体系统”同样采用图5所示的形式化坐标体系：选择笛卡儿3d坐标(x,y,z)及其对应的球坐标(r,θ，φ)描述天体“二体系统”(M,m)之3d空间(见图5(a)；式(6.20))；设定质点M(恒星)为坐标原点O，设想质点(行星)m在X-Y(θ=π/2)平面内运动(见图5(b)).

基于上述GOR天体“二体问题”之理想化条件或假设条件，我们将因循PGC对应原理，结合PGC逻辑路线1和PGC逻辑路线2，类比爱因斯坦之行星运动方程的逻辑，演绎推导GOR行星运动方程.

7.4.2 GOR理论与天体“二体系统”

在第6章之6.3和6.4中，我们已经获得了GOR场方程关于静态球对称引力场的真空解，包括近似解和精确解.针对天体之“二体问题”，基于GOR理论，将GOR场方程之精确解(见第6章之式(6.31)(6.32))代入GOR理论之线元方程和GOR理论之运动方程(“短程线”)，即可构建GOR天体“二体系统”理论模型，进而导出GOR行星运动方程.

GOR天体“二体系统”之线元公式——

如式(6.31)(6.32)所示，天体“二体系统”之GOR场方程解乃球坐标(r,θ，φ)之时空度规gμν=gμν(η,r,θ)：

gμν(η)=diag(g00,g11,g22,g33)=

diag(eξ,-eζ,-r2,-r2sin2θ)

(7.40)

于是，GOR线元公式可表述为

ds2=g00dx0dx0+g11dx1dx1+g22dx2dx2+g33dx3dx3=

eξη2dt2-eζdr2-r2dθ2-r2sin2θdφ2

(x0=ηt,x1=r,x2=θ,x3=φ;μ=0,1,2,3)

(7.41)

其中，r=0(代表质心)以及r=2GM/η2(代表M球面)均为GOR线元公式之奇点.

GOR行星运动之“短程线”方程——

将天体“二体系统”之GOR场方程解代入GOR理论之运动方程(即所谓“短程线”方程)，即可获得天体“二体系统”之GOR运动方程，即行星运动之GOR“短程线”方程式：

(x0=ηt,x1=r,x2=θ,x3=φ;μ=0,1,2,3)

(7.42)

式中：t为“观测时间”；τ为“固有时间”(原时).

与爱因斯坦广义相对论中的行星运动之“短程线”方程式一样，式(7.42)共包含4个方程式(μ=0,1,2,3)：1)t=t(τ)，2)r=r(τ)，3)θ=θ(τ)，4)φ=φ(τ).其中，t=t(τ)为时间方程；而r=r(τ)和θ=θ(τ)以及φ=φ(τ)则为空间方程.

7.4.3 方程式t=t(τ)与时空变换因子

基于式(7.40)之GOR度规gμν=gμν(η,r,θ)可得

(7.43)

令μ=0，则xμ=x0=ηt；由式(7.42)可知

(7.44)

对照式(7.42)与式(7.43)可得t之二阶微分方程式

(7.45)

对t之方程式(7.45)进行一次积分得

(7.46)

式中：Ct为常数；而Γ(η)=dt/dτ正是GOR理论中的时空变换因子.

依照GOR理论的概念，t之微分方程(7.45)所描述的是一般观测代理OA(η)之“观测时间”t与客观真实的“固有时间”τ的关系.式(7.46)意味着运动物体(行星)m之一般观测代理OA(η)的“观测时间”t不同于客观真实的“固有时间”(原时)τ.

7.4.4 方程式θ=θ(τ)与行星运动平面

基于式(7.40)之GOR度规gμν=gμν(η,r,θ)可得

(7.47)

令μ=2，则xμ=x2=θ；由式(7.42)可知

(7.48)

对照式(7.42)与式(7.47)可得θ之二阶微分方程式

(7.49)

不失一般性，假定某个初始时刻t=0，质点(行星)m运行在X-Y(θ=π/2)平面内，则

θ之方程式(7.49)及式(7.50)意味着，在GOR理论之“二体系统”理论模型(7.42)中，质点(行星)m的轨道平面是恒定不变的.这与开普勒轨道定律以及牛顿和爱因斯坦的行星运动方程之结论一致.

7.4.5 方程式φ=φ(τ)与开普勒面积定律

基于式(7.40)之GOR度规gμν=gμν(η,r,θ)可得

(7.51)

令μ=3，则xμ=x3=φ；由式(7.42)可知

对照式(7.42)与式(7.51)可得φ之二阶微分方程式

(7.53)

已知行星轨道平面是恒定的，不失一般性，可设质点(行星)m运行于X-Y(θ=π/2)平面，则φ之方程式(7.53)可写作

(7.54)

对φ之方程式(7.54)进行一次积分得

(7.55)

式中行星之速度矩hK=L/m为常数或不变量，自然地，行星角动量L=mhK也是常量或不变量.

这正是开普勒三定律之“面积定律(见图4(a)；式(7.3))：行星矢径r单位时间内扫过的面积相等.本质上，式(7.55)即角动量守恒定律：L=rmv是不变的.(特别注意，这力同样要求行星质量m为行星之“固有质量”，而非“相对论性质量”.)

这与牛顿之行星运动方程和爱因斯坦之行星运动方程的结论是一致的，同时，表明GOR之行星运动方程，以及牛顿和爱因斯坦的行星运动方程，皆可导出开普勒三定律之“面积定律”，或者说，皆可导出行星之角动量守恒定律：L=rmv是不变的.

7.4.6 方程式r=r(τ)与行星轨道

基于式(7.40)之GOR度规gμν=gμν(η,r,θ)可得

(7.56)

令μ=1，则xμ=x1=r；由式(7.42)可知

(7.57)

对照式(7.42)与式(7.56)可得r之二阶微分方程式

(7.58)

利用GOR线元公式(7.41)可得

(7.59)

于是，式(7.58)可重写作

(7.60)

已知行星轨道平面是恒定的，不失一般性，可设质点(行星)m运行在X-Y(θ=π/2)平面，则

(7.61)

这便是基于GOR理论建立的天体之“二体系统”理论模型——GOR行星轨道方程，是行星矢径r和行星轨道角度φ关于标准时间τ的二阶非线性微分方程式，其中，设定的行星轨道平面为：X-Y(θ=π/2).

7.4.7 GOR行星运动方程的比耐形式

基于式(7.55)，则式(7.61)可写作

(7.62)

实际上，GOR理论之天体“二体系统”理论模型(7.62)是GOR理论之运动方程(7.42)(“短程线”)中空间方程式r=r(τ)和θ=θ(τ)以及φ=φ(τ)的缩并，其中，设定了θ=π/2，并且，代入了dφ/dτ≡hK/r2.

然而，式(7.62)乃行星矢径r关于固有时间τ的二阶非线性微分方程式，缺少有关行星轨道角度φ的信息，不能独立地作为天体“二体系统”之理论模型，不能独立地描述行星之运动.通常，包括经典力学和爱因斯坦广义相对论，倾向于将天体“二体系统”理论模型表述为比耐方程的形式.

因循比耐方程式(7.4)的逻辑思想和逻辑方法，令u=1/r，则dφ/dτ=hK/r2=hKu2，且

(7.63)

代入式(7.62)即得

(7.64)

式中：G为万有引力常数；M为恒星质量；r为太阳M指向光子m的矢径；hK=r2dφ/dτ为行星m围绕恒星M运行之速度矩；η为一般观测代理OA(η)之信息波速度；u=u(φ)可视为行星m之运动轨迹.

这便是比耐形式的GOR行星运动方程，与爱因斯坦之行星运动方程(7.33)具有同构一致性对应关系，同样具有“行星轨道旋进项”，乃非标准的或非闭合的非线性椭圆微分方程.

根据OR理论，任意观测代理OA(η)之信息波速度η必须大于或者等于被观测对象m之速度v.式(7.64)中的被观测对象m是行星，因此，要求η≥v.

值得指出，客观真实的物理世界是唯一的.

行星- 恒星“二体系统”中，客观真实的行星m之运动轨迹必定也是唯一的.然而，式(7.64)中，u=u(η)，行星m之运动轨迹依赖于观测代理OA(η)，依赖于信息波之速度η.这意味着，不同观测代理，其呈现给观测者的行星运动轨迹及其轨道旋进是不一样的，皆非客观真实的进动或旋进.可见，观测的，未必即客观真实的，除非观测者能借助于理想观测代理OA∞(η→∞)观测行星m之运动.

7.5 GOR理论与行星轨道的旋进

牛顿之行星运动方程(式(7.5))无“行星轨道旋进项”.爱因斯坦之行星运动方程(式(7.33))含“行星轨道旋进项”：3GM/(c2r2)；GOR行星运动方程(式(7.64))含“行星轨道旋进项”：3GM/(η2r2).爱因斯坦之“行星轨道旋进项”依赖于光速c，而GOR之“行星轨道旋进项”则依赖于观测代理OA(η)之信息波速度η.OA(η)乃一般观测代理，理论上，其观测媒介可为任意物质运动形式，其传递观测信息的速度η可为任意物质运动速度.

基于PGC对应原理，经由PGC逻辑路线1，或者经由PGC逻辑路线2，因循7.3.4求解爱因斯坦之行星运动方程(式(7.33))的逻辑途径，皆可获得GOR行星运动方程(式(7.64))之解

(7.65)

对于行星轨道近日点，应成立：du/dφ=0.因此，对式(7.64)两端求关于φ的导数可得

(7.66)

若不计φcosφ，则

(7.67)

即sinφ=0，其解为φ=arcsinφ=2kπ(k=0,1,2,…).这意味着，若不计φcosφ，则行星轨道将与牛顿之行星运动方程一样，为一封闭的椭圆，不存在旋进.

考虑φcosφ：设行星运行一周之“进动”为Δφ，乃一小量(Δφ≪1)；令k=1，即行星围绕恒星运行一周(见图4(b)：行星由近恒星点P出发运行至下一近恒星点P′)，其扫过的角度应为φ=2π+Δφ.代入式(7.66)，并忽略高阶小量，则

(7.68)

式中η即一般观测代理OA(η)之信息波速度，可为任意物质运动速度，未必一定是光速c.

GOR理论之式(7.68)，既可计算牛顿之行星轨道旋进，也可计算爱因斯坦之行星轨道旋进.理想代理OA∞之下，η→∞，Δφ=0，行星无进动，与牛顿之行星运动方程的结论一致；而光学代理OA(c)之下，η=c，Δφ>0——水星每公转一周进动约0.102 9角秒，每100个地球年进动42.77角秒，自然与爱因斯坦之行星运动方程的所得结论一致.

实际上，观察GOR行星运动方程(式(7.64))之“行星轨道旋进项”3GM/(η2r2)和式(7.65)(7.66)可知，GOR天体“二体系统”理论模型所呈现出的行星近恒星点进动或行星轨道旋进，取决于观测代理OA(η)，取决于观测媒介传递行星运动信息的速度η：同一行星在不同观测代理之下会呈现出不同程度的进动或轨道旋进.这一事实表明，GOR天体“二体系统”理论模型，包括爱因斯坦之行星运动方程，其所呈现的所谓行星轨道旋进，并非客观真实的行星进动，本质上，是一种观测效应，乃观测代理OA(η)之观测局域性(η<∞)所导致的表观现象.理想代理OA∞之下，这种进动或轨道旋进的表观现象将不复存在.

观测相对论，包括OR理论和GOR理论，已经阐明：一切相对论性效应，包括狭义(惯性)相对论性效应和广义(引力)相对论性效应，皆观测效应和表观现象，其根源和本质在于观测代理存在观测局域性(η<∞).狭义相对论中的“时间膨胀”是一种光学观测效应，广义相对论中的行星进动也是一种光学观测效应，皆光学代理OA(c)之观测局域性(c<∞)所致.就观测代理OA(η)之局域性(η<∞)所导致的观测效应而言，观测者观测“二体系统”之行星公转一周呈现行星进动，与观测者观测时钟之时针运行一周呈现“时间膨胀”，其本质是相同的.

GOR理论并不怀疑实际的行星轨道存在旋进.实际上，限于各种非理想化的条件或因素，任何天体的运行轨道都不可能是理想的或标准的圆锥曲线，并且，也不能永远固定于某一特定的平面.

然而，无论牛顿万有引力论或爱因斯坦广义相对论，乃至GOR理论，其理想化的天体“二体系统”理论模型都不能预测真实的或实际的行星轨道旋进.正如我们反复强调过的，无论GOR理论之天体“二体系统”理论模型，还是牛顿或爱因斯坦天体“二体系统”理论模型，其前提条件中并无任何可供预测行星近恒星点之进动或行星轨道之旋进的先验信息或先验知识，诸如，坐标系的“岁差”或来自其他行星或天体的“摄动”，以及太阳不规则的形态和动态.

7.6 天体运行论的统一

宇宙中，天体的运行，激发了人类无限的好奇心.天体运行论，即关于天体运动的理论，探究天体如何运动，遵循什么规律运动，受什么驱之而运动.

一切天体之运动，源于万有引力，而非“时空弯曲”.GOR理论已经从理论上阐明了这一点.关于引力，物理学存在两大理论体系：一是牛顿万有引力论[53]；二是爱因斯坦广义相对论[15].因而，天体运行论也可以划分为两大理论体系：牛顿之天体运行论；爱因斯坦之天体运行论.自然地，牛顿天体运行论是经典力学和牛顿万有引力论的产物；而爱因斯坦之天体运行论则是爱因斯坦广义相对论的产物.显然，牛顿之经典天体运行论与爱因斯坦广义相对论之天体运行论的统一必然具有重要意义.

观测相对论，包括OR理论和GOR理论，概括统一了一切观测代理之物理学模型或物理学理论，包括理想代理OA∞之牛顿经典理论和光学代理OA(η)之爱因斯坦相对论.随着观测相对论之理论体系的逐步展开，OR和GOR理论概括统一不同观测代理之理论的特质会越来越充分地展现出来：OR理论之时空变换(所谓“广义洛伦兹变换”)，概括统一了伽利略变换和洛伦兹变换；GOR理论之引力场方程，概括统一了牛顿万有引力定律(之泊松方程形式)和爱因斯坦场方程；GOR理论之运动方程(“短程线”)，概括统一了牛顿第二定律之运动方程(直线)和爱因斯坦广义相对论之运动方程(“短程线”).现在，GOR天体运行论又将牛顿之经典天体运行论与爱因斯坦之基于广义相对论的天体运行论概括并统一起来.

宇宙，乃一切天体之总括，无疑，是巨大的和复杂的.如此，无论牛顿万有引力论，或爱因斯坦广义相对论，都尽力将其巨大而复杂的天体运动问题理想化，约化为天体之“多体问题”，乃至“三体问题”或“二体问题”，甚至，极度约化为天体之“单体问题”，正如本章之7.2和7.3所论述的.

基于GOR理论，本章建立了GOR之天体“二体系统”理论模型(式(7.63))，即GOR行星运动方程.作为一种新的天体运行论，GOR行星运动方程必定为天体物理学注入新的思想和新的认识，包括对牛顿天体运行论和爱因斯坦天体运行论的理解和认识，以及重新认识和理解行星轨道旋进等天文现象.

更重要地，GOR之天体“二体系统”理论模型(式(7.63))，概括并统一了牛顿之天体“二体系统”理论模型(式(7.5))和爱因斯坦之天体“二体系统”理论模型(式(7.33)).如

(7.69)

所示：光学代理OA(c)之下，η=c，GOR行星运动方程将严格地约化为爱因斯坦之行星运动方程；理想代理OA∞之下，η→∞，GOR行星运动方程将严格地约化为牛顿之行星运动方程.

如上所述，牛顿之行星运动方程，源于经典力学和牛顿定律，特别是牛顿万有引力定律；而爱因斯坦之行星运动方程则源于爱因斯坦广义相对论，源于爱因斯坦场方程和广义相对论运动方程.然而，牛顿之行星运动方程和爱因斯坦之行星运动方程，皆与GOR行星运动方程具有同构一致性对应关系，因而，被GOR理论概括并统一于GOR天体“二体系统”之理论模型.如此，经典力学之行星运动方程和相对论之行星运动方程，都只是GOR行星运动方程之特例，服务于特定的观测代理：爱因斯坦之天体运行论乃光学代理OA(c)之产物——光学代理OA(c)之下，我们的天文观测必定更合乎爱因斯坦之天体运行论；牛顿之天体运行论乃理想代理OA∞之产物——理想代理OA∞之下，我们的天文观测必定更合乎牛顿之天体运行论，并且更合乎客观真实的宇宙天体.

GOR之天体“二体系统”理论模型，概括并统一牛顿之天体“二体系统”理论模型和爱因斯坦之天体“二体系统”理论模型，这意味着：GOR行星运动方程，既与牛顿之行星运动方程逻辑上一致，又与爱因斯坦之行星运动方程逻辑上一致；同时，也印证了GOR理论及其行星运动方程理论上的正确性.

8 GOR理论与光之引力偏折

本章继续围绕爱因斯坦著名的三大预测，解析和测试GOR理论.光之引力偏折(引力场中光线之弯曲)问题，与第6章之行星进动问题一样，可以归结为类似的天体(m,M)“二体问题”：光子(m)在太阳(M)之引力场中运动.

针对光之引力偏折问题以及爱因斯坦对光之引力偏折的预测，本章基于GOR理论，运用GOR场方程和GOR运动方程，建立光子(m)和太阳(M)之“二体系统”理论模型.GOR理论力求基于PGC原理，结合PGC逻辑路线1和PGC逻辑路线2，类比爱因斯坦广义相对论之逻辑，演绎光子(m)掠过太阳(M)表面的运动方程.

GOR理论之光子运动方程可与牛顿万有引力论之光子运动方程以及爱因斯坦广义相对论之光子运动方程对照或类比，测试或验证GOR理论及其场方程和运动方程，解析光之引力偏折及其引力相对论性效应，进而，揭示牛顿引力偏折预测不同于爱因斯坦引力偏折预测的本质.

8.1 关于光之引力偏折

光之引力偏折，乃爱因斯坦为测试和检验其广义相对论而提出的著名的三大预测之一，意即：引力时空是“弯曲”的，因而，光线掠过太阳表面时必定会呈现出弯曲的状态.

原本，引力偏折预测是爱因斯坦基于其广义相对论重要逻辑前提之“等效原理”提出的.

等效原理(principle of equivalence)：惯性力与引力，或惯性力场与引力场，是等效的，对于一切物理观测和实验，具有局域的不可分辨性.

如图6(a)所示，一艘宇宙飞船在太空中飞行，一束光垂直于飞船固有坐标系O(x,y)之纵轴y从飞船左侧窗孔射入.理论计算可得光子在O(x,y)中的运动方程

(8.1)

式中：光线穿越窗孔时t=0，(X0,Y0)为窗孔坐标；v0为飞船初速度；a=|a|为飞船加速度；c即光速.

由式(8.1)可知，一般地，光子在飞船固有坐标系O(x,y)中，即在宇航舱内的宇航员看来，其轨迹如同一粒炮弹在地球表面飞行时一样，为一二次型曲线：

(8.2)

依式(8.1)(8.2)，如图6(a)所示，在宇航员看来：飞船静止时，射入的光线为水平直线；飞船匀速时，光线依然为直线，但略微有些倾斜；飞船加速时，光线会有些弯曲.

根据爱因斯坦之“等效原理”，惯性力与引力等效，惯性力场与引力场等效；宇航员不能确定飞船处于加速(a)状态或处于重力场(g=-a)中.因此，如图6(b)所示，宇航员位于任意星球表面或在任意重力场中，观测到掠过星球表面的光线，必定如同其在飞船内观测到的光线一样，是弯曲的.这便是爱因斯坦基于“等效原理”做出的光之引力偏折预测.

图6 等效原理与引力偏折Fig.6 Principle of equivalence and gravitational deflection

值得指出，爱因斯坦认为，光之引力偏折乃引力时空弯曲所致，而时空弯曲乃物质堆积所致.

实际上，牛顿万有引力论也能对光之引力偏折做出预测：作为物质粒子，光子与炮弹并无二致.在引力场中，光源发射的光子如同出膛的炮弹，受万有引力作用，其运动轨迹必定是弯曲的.并且，对于重力场g，依式(8.1)(8.2)：a=|g|，可对光之引力偏折角做出定量预测.当然，依牛顿万有引力论，光线的弯曲并非时空弯曲所致，而是物质间的引力相互作用.

广义相对论正式建立之前，爱因斯坦基于其“等效原理”做出的光子引力偏折预测只能是定性的：光线在引力场中会弯曲.爱因斯坦试图定量地预测光之引力偏折角，而他所能利用的计算模型只能是式(8.1)(8.2)描述的运动学模型.特别值得注意，运动学方程(8.1)(8.2)是伽利略- 牛顿理论的产物，是理想代理OA∞的产物.因此，不出所料，那时，爱因斯坦计算得出的光之引力偏折角与牛顿万有引力论相同.

广义相对论正式建立之后，有了场方程，爱因斯坦利用其场方程近似解(式(6.3))，获得了广义相对论光之引力偏折角的理论值.特别令人注目的是，爱因斯坦广义相对论这一理论值是牛顿万有引力论的2倍.为了测试其光之引力偏折预言，验证其“等效原理”和广义相对论，爱因斯坦构思了利用日食观测星光掠过太阳表面的实验.

日全食与掠过太阳表面的星光：如图7所示，位于太空深处A之恒星S辐射的光或光子，掠过太阳表面，飞向地球；依“等效原理”和广义相对论，太阳(物质和能量)周围之时空是弯曲的，因而，光子飞行轨迹会弯曲，在地球观测者看来，恒星S位于B之方向，与A之方向存在一个的偏折角δ，并且，这一光之引力偏折现象可在日全食发生的时候观测到.

借助日全食观测掠过太阳表面的星光是一个好的构思，否则，星光将淹没于太阳的光芒，难以观测.

星光偏折角之理论值：爱因斯坦广义相对论之星光偏折角δE预测：δE=1.75″=2δN；牛顿万有引力论之星光偏折角预测：δN=0.875″=δE/2.

如此，物理学界乃至全世界翘首以盼，期待着测试和验证星光之引力偏折预测的历史时刻，期待着爱因斯坦广义相对论与牛顿万有引力论的对决.

1919年5月29日，这一历史时刻到来了[75]：这一天，地球可观测到日全食.为了验证爱因斯坦广义相对论之引力偏折预测，英国天文学家爱丁顿率领的团队于1919年3月从英国出发，沿西非海岸赶赴西非的普林西比岛，开展人类历史上最为重要的一次日全食观测活动.爱丁顿团队利用日全食实际观测到星光偏折角：δ=1.61″±0.40″.几乎同一时间，在巴西的索布拉尔，另一位英国天文学家戴森率领的团队利用日全食观测到星光偏折角：δ=1.98″±0.16″.

图7 引力偏折的预测和验证Fig.7 Prediction and verification of gravitational deflection

爱丁顿和戴森的日食观测数据倾向于支持爱因斯坦广义相对论[76].观测结论公布后，科学界普遍接受了爱因斯坦广义相对论，认为日全食之观测，意味着爱因斯坦广义相对论战胜了牛顿万有引力论：牛顿错了；爱因斯坦是正确的！英国《泰晤士报》为此发表了整版新闻：《科学革命——牛顿的思想被推翻》.

正是这一次对日全食的观测，奠定了爱因斯坦广义相对论在物理学界的神圣地位，而牛顿万有引力论则被视为其“宏观弱场低速”之近似.

牛顿万有引力论真地错了吗？

爱因斯坦广义相对论真地正确吗？

日食观测活动及其观测数据和观测结论公布之后，爱丁顿写了一首诗以表达自己的感悟，大意是：

“啊！就让智慧去检验吧.

光也有重量，至少这件事可以确定.

还有一件事是确定的，余者仍有争议：

光线，当它接近太阳时，不再直行.”

爱丁顿诗中的感悟是理性而审慎的.

根据日全食之观测，爱丁顿肯定了光线在引力场中会弯曲.然而，值得注意，在爱丁顿看来，其日全食之观测可以十分确定的是：“光也有重量.”这里，爱丁顿向我们传递了2点重要的信息：第一，光子有“重量”，并且，爱丁顿之所谓“重量”，似乎是指光子之“静止质量”或“固有质量”，而非“相对论性质量”；第二，光线的弯曲是其“重量”所致，换句话说，乃引力所致，而非“时空弯曲”.爱丁顿对光或光子“重量”的认识是朴素的，与OR理论之结论一致.根据OR理论[2]：光子，乃至一切物质粒子，皆具有“静止质量”，并且，是固有的和具有引力效应的.而爱丁顿对光线弯曲之本质的认识，则符合牛顿万有引力论和GOR理论.

实际上，之前的章节中，GOR理论已经阐明，客观真实的时空是平直的，不会因为物质或能量之分布而弯曲.因此，就引力时空中光之引力偏折的本质而言，牛顿及其万有引力论是正确的：光之引力偏折乃引力作用使然，而非时空弯曲.

就光学观测中光之引力偏折的现象而言，爱因斯坦广义相对论之预测似乎更接近于日全食之观测.天文观测技术的发展，包括射频测量技术(redio frequency measurement)和天体卫星测量(astrometric satellite measurement)技术，进一步提高了光之引力偏折观测精度[60，77].2017年8月21日出现了一次横贯美国的日全食；观测人员在怀俄明州对其展开观测，获得了光之引力偏折有史以来最为精确的结果[78]：星光偏折角δ=1.751 2″，其不确定度仅为3.4%.这一观测结果与爱因斯坦的预言极其吻合，自然地，是对爱因斯坦广义相对论的支持.

然而，根据OR和GOR理论，观测，并不代表客观真实：观测的未必就是客观的或真实的.

就目前的技术水平而言，人类的天文观测，无论是光学天文学还是射电天文学，皆归属于光学代理OA(c)，传递天文信息的媒介是光或电磁相互作用，其信息波速度即光速c.爱因斯坦广义相对论是光学代理OA(c)之理论；因而，日食观测结果与爱因斯坦光之引力偏折预言一致，并不令人惊奇，是可以理解的，甚至，是必须的.

OR和GOR理论已经阐明，光学代理OA(c)存在观测局域性(c<∞)，其观测，包括光之引力偏折的日全食观测，存在观测效应或表观现象，并不完全客观真实.就此而言，爱因斯坦广义相对论的正确性，只是观测上或现象上的正确性，可谓“现象主义之正确性”(phenominalistic validity).

特别值得注意：爱因斯坦构思的日全食之星光观测，是专为光学代理OA(c)打造的，其中，光子，既是被观测对象，又是“信息子”.如图7所示，观测者或观测器不能观测到光子真实的运动轨迹，只能在光子抵达观测点(眼睛或观测器所在位置)时，将其抵达时的朝向作为光源(星星)所在位置的方向.然而，观测者如此看到或观测到的，并非客观真实的星星，而是星星之映像，一种表观现象而已.

牛顿万有引力论乃理想代理OA∞之理论，其引力偏折问题中的被观测对象仍然是光子，然而，传递光子信息的“信息子”并非光子自身，而是OA∞之理想化的信息子，动量无穷小；信息波并非光波，而是OA∞之理想化的信息波，速度无穷大.

GOR理论将会阐明，如果我们能够借助理想代理OA∞观测光之引力偏折，那么，日全食之星光观测必定会与牛顿万有引力所预测的光之引力偏折一致，倾向于支持牛顿万有引力论，而非爱因斯坦广义相对论.在此意义上，牛顿万有引力论才是更为正确的引力论，其光之引力偏折更为符合客观真实的光之引力偏折.

本章将基于第6章静态球对称引力时空之GOR场方程真空解以及GOR理论之天体“二体系统”理论模型，计算星光掠过太阳表面时的偏折角.我们会发现，不同的观测代理，将观测到不同程度的引力偏折或不同的星光偏折角.据此，类比牛顿万有引力论和爱因斯坦广义相对论，GOR理论将为我们解析光之引力偏折预测和观测中的现象与本质.

8.2 牛顿万有引力论与光之引力偏折

牛顿万有引力论也能预测光之引力偏折.

根据牛顿万有引力论，光之引力偏折的道理很简单：引力场中，飞行的光子如同出膛的炮弹，受引力作用，其轨迹自然是弯曲的.

原本，日全食之星光引力偏折观测实验乃爱因斯坦专为测试或验证其广义相对论而构思的，却同样可测试或验证牛顿万有引力论和GOR理论.

8.2.1 牛顿之引力偏折问题

如图7所示，爱因斯坦构思的星光掠过太阳之日全食观测实验中，光之引力偏折问题可归结为类似行星- 恒星之天体“二体问题”：光子- 太阳“二体问题”.类似行星- 恒星“二体系统”理论模型，基于牛顿万有引力论，可构建光子- 太阳“二体系统”理论模型；进而，计算星光引力偏折角.

行星- 恒星之“二体问题”中，被观测对象是行星；而光子- 太阳之“二体问题”中，被观测对象则是光子.与其行星- 恒星“二体系统”一样，其光子- 太阳“二体系统”理论模型也是极度理想化的，可如下描述.

光子- 太阳之“二体系统”：(M,m)，光子m受太阳M引力作用，在太阳M之引力场中运动.

光子- 太阳“二体系统”之理想化条件：基于牛顿万有引力论，光子- 太阳之“二体系统”(M,m)设立了或隐喻着如下理想化条件.

超距引力作用：引力乃超距作用，辐射速度无穷.

孤立质点体系：光子- 太阳“二体系统”(M,m)为一孤立体系，光子m和太阳M皆可视为质点，太阳M静止，光子m在太阳M之引力场中运动，不受太阳M和光子m之外物质或能量的影响.

理想观测代理OA∞：理想化的信息波速度无穷大，光子m运动信息的传递无须时间；理想化的信息子动量无穷小，如此，其对被观测对象(包括光子)之运动无扰动.

理想观测者：观测者O借助理想代理OA∞，基于太阳M的视角观测光子m之运动，理论上，O相对于太阳M静止且处于引力势之零势位.

光子- 太阳“二体系统”之形式化坐标：如图7所示，选择笛卡儿3d坐标(x,y,z)及其对应的球坐标(r,θ,φ)表达光子- 太阳“二体系统”(M,m)之3d空间(见图7(b)；式(6.6))；设定太阳M为坐标原点O，光子m在太阳M之引力场X-Y(θ=π/2)平面内运动(见图7(c)).

实际上，光之引力偏折问题，可进一步理想化或约化为“单体问题”：太阳M是静止的，只涉及或只观测光子m在太阳M之引力场中的运动.

特别需要指出：在牛顿光之引力偏折问题中，光子乃被观测对象，其观测信息的传递，依赖于理想代理OA∞之理想化的“信息子”.

8.2.2 牛顿之光子运动方程

正如之前所述，星光掠过太阳之引力偏折问题，可以归结为类似第7章的行星- 恒星之天体“二体问题”：光子- 太阳“二体问题”.并且，如图7所示，光子- 太阳“二体系统”同样选择了与图5之行星- 恒星“二体系统”相同的坐标体系.因此，因循或类比第7章7.2“牛顿之行星运动方程”中的逻辑路线，基于牛顿万有引力论，即可在球坐标系(r,θ,φ)中建立与牛顿行星运动方程(式(7.5))形式上相同的光子- 太阳方程，或称“牛顿光子运动方程”：

(8.3)

式中：G为万有引力常数；M为太阳质量；RS为太阳半径；r为太阳M指向光子m的矢径；hK=r2dφ/dτ为光子m之速度矩；c即光速.

hK为光子速度矩，且hK=L/m，其中，L=mvr为光子m之“动量矩”(即角动量)，m又代表光子质量(牛顿力学中，m必定指光子“静止质量”)，而v则为光子m在引力场中的运动速度.

光子m掠过太阳表面(图7(c)之点F：光子m之近日点)时，其飞行速度v=rdφ/dτ≈c，矢径r≈RS.

因此，式(8.3)中光子之速度矩hK为

(8.4)

8.2.3 牛顿之光子飞行轨迹

如第7章之7.2所述，束缚于恒星，行星运行轨道之微分方程(7.5)(7.6)代表圆或椭圆.然而，光子之质量远小于行星质量，而速度则远高于行星速度，不会被太阳束缚，其运行轨迹自然不会是圆或椭圆.

光子运动方程(8.3)之解，形式上必定与行星- 太阳“二体系统”运动方程(7.5)之解相同，因循第7章7.2“牛顿之行星运动方程”的逻辑路线，解之可得

(8.5)

式中：积分常数CS取决于光子m之初始角动量L及其机械能E；积分常数φ0为光子轨道初始角，调整时间零点，或者，绕Z轴转动X-Y平面，可将其设定为特定值；e为光子m之轨道偏心率.

式(8.5)意味着，根据牛顿万有引力论，光子运动方程乃一标准的圆锥曲线.

(8.6)

故可设定：φ0=π/2；而CS则为：CS=1/RS.

如此，依图7(c)，星光轨迹式(8.5)可确定为

(8.7)

式中e为牛顿光子运动方程之轨道偏心率.

如第7章之7.2所述，天体“二体系统”(M,m)中，天体m(包括行星和光子)之轨道偏心率e依赖于引力常量数G和引力场源M，以及运动天体m之初始机械能E和角动量L.因此，光子m之轨道偏心率e也可依经典天体力学公式(7.7)计算.

光子m之机械能E和角动量L皆可视为守恒量.如式(8.4)，考虑光子m掠过图7(c)太阳表面之点F(光子m之近日点)时的情形，v≈c和r≈RS，则

(8.8)

于是，光子m之运行轨迹的偏心率

(8.9)

结果与式(8.7)相同.

根据国际标准组织之推荐值可知：

光速c=2.997 924 5×108m/s;

万有引力常数G=6.674 30×10-11m3/(kg·s2);

太阳质量M=1.988 47×1030kg;

太阳半径RS=6.96×108m.

由式(8.7)可计算光子m之运行轨迹的偏心率

(8.10)

其中，光子m之偏心率e≫1，这意味着，星光掠过太阳表面的轨迹乃一双曲线.

根据牛顿光子运动方程(8.3)之解(式(8.7))以及式(8.10)之偏心率e可知，基于牛顿万有引力论的理想化光子- 太阳“二体系统”模型，其光子运动轨迹乃一标准的双曲线.由此可见，即使依据牛顿万有引力论，光线在引力场中也会是弯曲的！

然而，牛顿万有引力论所预测的星光引力偏折角却不同于爱因斯坦广义相对论所做出的预测.

8.2.4 牛顿之星光引力偏折角

现在，基于光子运动方程(8.3)之解(8.5)以及光子运动轨迹偏心率方程(8.7)，即可计算星光引力偏折角，自然地，是基于牛顿万有引力论计算所得的星光引力偏折角，记作：δN，可称“牛顿之星光引力偏折角”.

如图7(c)所示，光子m由遥远的星星S出发，掠过太阳表面，抵达远离太阳M的地球时，可视其坐标量：r→∞，u→0，φ→π+α，其中，α为一小量.

于是，依式(8.5)，成立：

(8.11)

显然，α乃一小量，sinα≈α.因此，依牛顿万有引力论，星光掠过太阳时，牛顿之星光引力偏折角为

(8.12)

牛顿万有引力论之预测：星光掠过太阳的偏折角为0.875 25″.(这一预测是对客观真实的光子运动轨迹及其偏折角的预测，其中，隐喻着一个假设或条件：观测代理乃理想代理OA∞.)

的确，牛顿万有引力论预测的星光引力偏折角与地球上的光学观测者之实际观测值不符：其0.875 25″之预测，似乎只是美国怀俄明州之日全食星光引力偏折角实际观测值1.751 2″的1/2[78].

特别值得注意，无论爱丁顿或戴森的日全食观测[75-76]，还是美国怀俄明州的日全食观测[78]，都是光学代理OA(c)之观测.而测试或验证牛顿万有引力论之星光引力偏折预测，需要对照的应该是理想观测代理OA∞，而非光学代理OA(c).

稍后GOR理论将会阐明：并非牛顿之错，而是观测之错；并非牛顿万有引力论存在偏差，而是光学代理OA(c)之观测存在偏差.牛顿万有引力论之预测是客观真实的光之引力偏折；爱因斯坦广义相对论之预测是光学代理OA(c)所呈现的光之“引力偏折”，而光学代理OA(c)所呈现的光之偏折并非完全客观真实，其中，包含着观测效应和表观现象.

其实，无论牛顿之星光引力偏折角δN还是爱因斯坦之星光引力偏折角δE，都只是GOR理论之星光引力偏折角δGOR的特例.

8.3 爱因斯坦广义相对论与光之引力偏折

爱因斯坦光之引力偏折预言，源于其“时空弯曲”的思想：引力时空是弯曲的，因而，引力场中光或光子的轨迹必定也是弯曲的.

爱因斯坦之“时空弯曲”的思想观念极其玄妙深奥.人们可以理解空间弯曲，而时间弯曲却是很难想象的.或许，爱因斯坦的本意，并不在于通过观测实验证明光之引力偏折，而在于通过光之引力偏折，证明时空是“弯曲”的.

然而，光之引力偏折，并不意味着“时空弯曲”，牛顿之万有引力论也能诠释光之引力偏折.

为了阐明光之引力偏折，广义相对论正式建立之前，爱因斯坦运用其构思的“等效原理”，以图6所示的方式和逻辑，阐述其光之引力偏折的预言；广义相对论正式建立之后，爱因斯坦基于其场方程获得了星光引力偏折角的理论值.

无论如何，爱因斯坦广义相对论，给予我们不同于牛顿万有引力论的思想和认识，并且，得出了不同于牛顿之星光引力偏折角的理论值.

重温爱因斯坦光之引力偏折的预言及其广义相对论的理论计算，将有助于我们理解GOR理论.

8.3.1 爱因斯坦之引力偏折问题

如8.2.1之“牛顿引力偏折问题”所述，光之引力偏折问题可归结为类似行星-恒星之天体“二体问题”：光子- 太阳“二体问题”.因而，基于爱因斯坦广义相对论，可构建光子- 太阳“二体系统”理论模型；由此，可计算星光引力偏折角.

爱因斯坦光之引力偏折问题中，与其行星- 恒星“二体系统”一样，其光子- 太阳“二体系统”之理论模型也包含着理想化条件，可如下描述.

光子- 太阳之“二体系统”：(M,m)，太阳M周围时空是弯曲的，光子m在太阳M弯曲的时空中运动.

光子- 太阳“二体系统”之理想化条件：基于爱因斯坦广义相对论，光子- 太阳之“二体系统”(M,m)设立了或隐喻着如下理想化条件.

超距引力作用：引力乃超距作用，辐射速度无穷.

上述理想化条件，与牛顿光之引力偏折问题中的“超距引力作用”假设和“孤立质点体系”假设相同.然而，爱因斯坦光之引力偏折问题并不包含“理想观测代理”和“理想观测者”之假设，取而代之的是“光学观测代理”和“光学观测者”条件.

光学观测代理与光学观测条件：爱因斯坦光之引力偏折问题中的观测代理，是实际的和非理想化的，乃特定之观测代理，隐喻着如下观测条件.

光学观测代理OA(c)：爱因斯坦之日全食星光观测实验的观测代理OA(η)乃光学代理OA(c)，其信息波速度η即光速c，光子m之运动信息的传递需要时间；其信息子即光子自身.

光学观测者：观测者O借助光学代理OA(c)，基于M之视角观测光子m之运动，理论上，O相对于M静止且处于引力势之零势位.

光子- 太阳“二体系统”之形式化坐标：与8.2之牛顿光子- 太阳“二体系统”一样，选择如图7所示的笛卡儿3d坐标(x,y,z)及其对应的球坐标(r,θ,φ)表达光子- 太阳“二体系统”(M,m)之3d空间(见图7(b)；式(6.6))；设定太阳M为坐标原点O，光子m在太阳M之引力场X-Y(θ=π/2)平面内运动(见图7(c)).

如8.2所述，光之引力偏折问题及其光子- 太阳“二体系统”可进一步地理想化或约化为“单体问题”：太阳M是静止的，只涉及或只观测光子m在太阳M之引力场中的运动.

特别需要指出：在爱因斯坦光之引力偏折问题中，光子既是被观测对象，又是光学代理OA(c)之信息子：光子之信息的携带和传递依赖于光子自身.如此，光子之运动轨迹不存在受信息子扰动的问题，然而，观测者只能观测到光子运动的抵达或结果，无法观测到光子运动的轨迹和过程.

8.3.2 爱因斯坦之光子运动方程

广义相对论正式建立之后，爱因斯坦利用其场方程近似解(式(6.3))及其线元ds之公式(6.4)，求解星光引力偏折角.Schwarzschild[57]得到场方程精确解之后，即可建立广义相对论之光子运动方程，进而，求解星光引力偏折角[74].

爱因斯坦广义相对论也可将星光掠过太阳之引力偏折问题归结为类似第7章的行星- 恒星之天体“二体问题”，并且，如图5、7所示，其光子- 太阳“二体系统”与行星- 恒星“二体系统”之坐标体系相同.因循第7章7.3之“爱因斯坦之行星运动方程”的逻辑路线，基于爱因斯坦广义相对论，即可在球坐标系(r,θ,φ)中建立与爱因斯坦之行星运动方程(式(7.33))形式上相同的光子- 太阳方程，或称“爱因斯坦光子运动方程”：

(8.13)

式中：G为万有引力常数；M为太阳质量；r为太阳M指向光子m的矢径；hK=r2dφ/dτ为光子m之速度矩；c即光速.

特别注意，作为光学代理OA(η)之理论，爱因斯坦广义相对论中，速度达到光速c的被观测对象(如光子- 太阳“二体系统”中的光子m)，其线元ds=0.实际上，更一般地，基于PGC原理，由GOR理论之一般观测代理OA(η)的线元方程ds=gμν(η)dxμdxν可知，被观测对象之速度v→η时，其线元ds→0.

严格的意义上，ds→0之情形只在m既是被观测对象，又是传递m之运动信息的信息子时，才会成立.这时，m之运动速度v严格地等同于信息波速度η.

GOR理论关于“观测代理”之定义1.1中，任意观测代理OA(η)，其信息波速度η应为信息波或信息子之实时速度.对于光学代理OA(c)而言，x0=ct中的c应为光波或光子之实时速度，未必是真空光速.在爱因斯坦构思的通过日食观测星光掠过太阳表面时的引力偏折实验中，光子之运动信息由光子自身携带并传递：光子，既是被观测对象，又是传递光子运动信息的信息子.这时，作为被观测对象的光子与作为信息子的光子，其速度自然为同一速度，无论光子之速度在引力场中是否衰减.如此，光子运动轨迹之时空线元ds必定为零：ds=0.

因此，式(8.13)中，在光子既是被观测对象又是信息子的情形下，光子之速度矩hK为

(8.14)

如此，爱因斯坦光子运动方程(8.13)被约化为

(8.15)

与牛顿光子运动方程(8.3)不同，爱因斯坦光子运动方程(8.15)并非线性方程，而是非线性微分方程.

8.3.3 爱因斯坦之光子飞行轨迹

求解爱因斯坦光子运动方程(8.15)，可得光学观测代理OA(c)之视角下光子m的飞行轨迹.爱因斯坦光子运动方程(8.15)为一非线性微分方程，难以求解；幸而有近似解(参见文献[74]).

若太阳质量M=0，则式(8.15)可约化为

(8.16)

解之可得

u=CScos(φ-φ0)

(8.17)

式中CS和φ0为积分常数.

观察图7(c)可知，φ=π/2时(光子m掠过太阳M表面之点F：光子m之近日点)，u=1/r=1/RS.代入式(8.17)可得

(8.18)

调整时间零点，可将φ0设定为π/2：φ0=π/2；而CS则为1/RS：CS=1/RS.代入式(8.17)，可得式(8.16)之解，也即式(8.15)之通解ug：

(8.19)

式(8.19)即光子m平行于X轴掠过太阳表面之点F(光子m之近日点)时的情形.可见，在没有引力势场(M=0)的时空中，光子的飞行轨迹乃一直线.

(8.20)

式(8.20)有如下解，即式(8.20)之特解us：

(8.21)

于是，式(8.20)之解u即通解ug与特解us之和为

(8.22)

如图7(c)所示，可设φ=π+φ(α≥φ≥-α)，其中，α和|φ|皆为小量，cos2(π+φ)=1；代入式(8.22)右端第二项可得

(8.23)

式中：e=RSc2/GM为牛顿光子轨迹之偏心率；而=e/2 =RSc2/GM则为爱因斯坦光子轨迹之偏心率.

对照或类比式(8.7)可知，式(8.23)为一标准的双曲线.因为式(8.22)乃爱因斯坦光子运动方程(8.15)之近似解，式(8.23)乃式(8.22)之近似表达式，所以爱因斯坦光子运动方程并非标准的双曲线，如式(8.23)所示，在基于爱因斯坦广义相对论的光子- 太阳“二体系统”模型中，光子运动轨迹乃近似之双曲线.

观察式(8.23)可以发现：爱因斯坦光子运动方程之轨道偏心率=RSc2/(2GM)，只是牛顿光子运动方程之轨道偏心率e=RSc2/(GM)的1/2.这意味着，光学代理OA(c)所呈现的引力场之星光轨迹比理想代理OA∞更为弯曲，其偏折角自然会更大.

8.3.4 爱因斯坦之星光引力偏折角

现在，基于光子运动方程(8.15)之解(式(8.22)，可计算星光引力偏折角.自然地，这是基于爱因斯坦广义相对论计算所得的星光引力偏折角，记作δE，可称“爱因斯坦之星光引力偏折角”.

如图7(c)所示，光子m由遥远的星星S出发，掠过太阳表面，抵达远离太阳M的地球时，可视其坐标量：r→∞，u→0，φ→π+α，其中，α为一小量.

于是，依式(8.22)，成立：

(8.24)

式中α为一小量，sin(π+α)≈-α，cos(π+α)≈-1.

因此，依爱因斯坦广义相对论，星光掠过太阳时，爱因斯坦之星光引力偏折角为

(8.25)

爱因斯坦广义相对论预测：在地球上的观测者看来，星光掠过太阳的偏折角为1.750 5″.(这一预测隐喻着一个条件：观测代理乃光学代理OA(c) ).

对照式(8.25)和式(8.12)可知，爱因斯坦之星光引力偏折角δE是牛顿偏折角δN的2倍：δE=2δN，符合实际观测值，与美国怀俄明州之日全食星光偏折角实际观测值1.751 2″精确相符[78].

这一结论并令人意外.如前所述，无论爱丁顿或戴森的日全食观测[75-76]，还是美国怀俄明州的日全食观测[78]，都是光学代理OA(c)之观测.自然地，爱因斯坦广义相对论作为光学观测理论，其星光引力偏折角δE应该符合光学代理OA(c)之观测.

如前所述，与牛顿偏折角δN一样，爱因斯坦之星光引力偏折角δE也只是GOR理论所预测的光之引力偏折角δGOR的一个特例.

8.4 GOR理论与光之引力偏折

GOR理论也能预测光之引力偏折.

GOR理论乃一般观测代理OA(η)之理论.可以预计，GOR理论预测星光掠过太阳表面之偏折角，或称“GOR星光引力偏折角”：δGOR=δGOR(η)，依赖于观测代理OA(η)之信息波速度η——不同的观测代理将会有不同的GOR星光引力偏折角.这意味着，对于同一光之引力偏折场景，不同的观测代理将会呈现出不同程度的光之引力偏折.

特别地，牛顿偏折角δN和爱因斯坦偏折角δE，都将成为GOR星光偏折角δGOR之特例.

8.4.1 GOR理论之引力偏折问题

对于GOR理论，光之引力偏折问题同样地可归结为类似行星- 恒星之天体“二体问题”：光子- 太阳“二体问题”.因而，GOR理论也可构建其光子- 太阳“二体系统”理论模型，进而，分析GOR理论之引力偏折问题，计算光GOR星光引力偏折角.

与GOR理论之行星- 恒星“二体系统”一样，GOR理论之引力偏折问题中，GOR光子- 太阳“二体系统”之理论模型也包含着理想化条件，可如下描述.

光子- 太阳之“二体系统”：(M,m)，太阳M向周围时空辐射引力，光子m在太阳M之引力时空中运动.

光子- 太阳“二体系统”之理想化条件：基于GOR理论，光子- 太阳之“二体系统”(M,m)包含着如下理想化条件.

超距引力作用：引力乃超距作用，辐射速度无穷.

上述理想化条件，与牛顿和爱因斯坦光之引力偏折问题中的“超距引力作用”假设和“孤立质点体系”假设相同.然而，GOR光之引力偏折问题并不包含“理想观测代理”或“光学观测代理”之假设，取而代之的是“一般观测代理”条件.

一般观测代理与一般观测条件：GOR理论之光子- 太阳“二体问题”中，观测代理即GOR理论之一般代理，而非特定代理，隐喻着如下观测条件.

一般观测代理：GOR理论光子- 太阳“二体系统”(M,m)之观测代理，乃GOR理论之一般观测代理OA(η).理论上，一切物质运动形式皆可为其观测媒介.信息波速度η可为任意物质运动速度，但要求其速度大于或等于作为被观测对象的光子m之运动速度；信息子可为任意物质粒子，但要求其动量足够小，不会对光子运动产生显著影响.

一般观测者：观测者O借助于一般观测代理OA(η)，基于M的视角观测光子m之运动，理论上，O相对于M静止且处于引力势之零势位.

光子- 太阳“二体系统”之形式化坐标：如同牛顿和爱因斯坦之光子- 太阳“二体系统”，选择如图7所示的笛卡儿3d坐标(x,y,z)及其对应的球坐标(r,θ,φ)表达光子- 太阳“二体系统”(M,m)之3d空间(见图7(b)；式(6.6))；设定太阳M为坐标原点O，光子m在太阳M之引力场X-Y(θ=π/2)平面内运动(见图7(c)).

8.4.2 GOR理论之光子运动方程

GOR理论同样将星光掠过太阳之引力偏折问题归结为类似第7章中的行星- 恒星之天体“二体问题”，并且，如图5、7所示，其光子- 太阳“二体系统”与行星- 恒星“二体系统”之坐标体系相同.

基于GOR理论，因循第7章7.4“GOR行星运动方程”的逻辑路线，即可在球坐标系(r,θ,φ)中建立与GOR行星运动方程(式(7.33))形式上相同的光子- 太阳方程，或称“GOR光子运动方程”：

(8.26)

式中：G为万有引力常数；M为太阳质量；r为太阳M指向光子m的矢径；hK=r2dφ/dτ为光子m之速度矩；η即一般观测代理OA(η)之信息波速度；u=u(φ)=1/r(φ)可视为光子m之运动轨迹.

GOR理论之光子运动方程(8.26)概括了牛顿光子运动方程(8.3)和爱因斯坦光子运动方程式(8.15)乃至一般观测代理OA(η)(η∈(c,+∞))之光子运动方程.

牛顿光子运动方程：η→∞.

考虑光子m之近日点，即光子掠过图7(c)中太阳表面之点F时的情形，光子m之速度v=rdφ/dτ≈c及其矢径r≈RS.因此，如式(8.4)所示，光子m之速度矩hK=r2dφ/dτ=rv≈RSc.

η→∞时，观测代理OA(η)即理想观测代理OA∞；这时，式(8.26)中，u=u∞乃理想代理OA∞所呈现的光子m之运动轨迹，其中，右端为

(8.27)

如此，GOR光子运动方程(8.26)约化为牛顿光子运动方程(对照8.2.2之式(8.3))：

(8.28)

爱因斯坦光子运动方程：η→c.

η→c时，观测代理OA(η)即光学观测代理OA(c)；这时，式(8.26)中，u=u(c)乃光学代理OA(c)所呈现的光子m之运动轨迹，其中，光子m既是被观测对象又是传递光子m的信息子：作为被观测对象的光子m之速度v与作为信息子的光子m之速度η相同.因此，如8.3.2所述，光子m之线元ds=0.

于是，式(8.26)右端满足

(8.29)

如此，GOR光子运动方程(8.26)约化为爱因斯坦光子运动方程(对照8.3.2之式(8.15))：

(8.30)

一般观测代理之光子运动方程：∞>η>c.

根据OR理论，任意观测代理OA(η)之信息波速度η须大于或者等于被观测对象m之速度v.式(8.26)中，被观测对象m是光子，其速度v≈c.因此，要求η≥c.

考虑一般观测代理OA(η)之情形(∞>η>c)，则u=u(η)乃一般观测代理OA(η)所呈现的光子m之运动轨迹，将光子之速度矩hK=RSc代入式(8.26)，则GOR光子运动方程(8.26)为

(8.31)

综上所述，无论牛顿之光子运动方程(8.3)(8.28)，还是爱因斯坦光之子运动方程(8.15)(8.30)，或一般观测代理OA(η)之光子运动方程(8.31)，皆统一于GOR理论之光子运动方程(8.26).

值得注意，GOR光子运动方程(8.26)中，u=u(η)：光子m之运动轨迹依赖于观测代理OA(η)，依赖于OA(η) 之信息波速度η，不同的观测代理，其呈现给观测者的光子运动轨迹及其星光引力偏折角将会是不同的.然而，客观真实的物理世界必定是唯一的.光子-太阳“二体系统”中，光子m之客观真实的运动轨迹必定也是唯一的.可见，观测所得光子运动轨迹或引力偏折未必是其客观真实的轨迹或偏折.除非，观测者能借助理想代理OA∞观测光子m之运动.

8.4.3 GOR理论之光子飞行轨迹

基于GOR光子运动方程(8.26)，可以预计，对于不同的观测代理或不同的信息波速度，光子运动轨迹将会呈现出不同程度的弯曲和不同的偏折角.

若能求解GOR光子运动方程(8.26)，则可获得观测给定代理OA(η)之视角下光子m的飞行轨迹.

然而，GOR光子运动方程(8.26)乃一非线性微分方程，难以求解，除非η→∞，式(8.26)约化为牛顿光子运动方程(8.28).GOR光子运动方程(8.26)中，观测代理OA(η)之信息波速度η覆盖了[c,+∞)，特别地，η=c可能为式(8.26)引力偏折角的非连续点.

幸运的是，在[c,+∞)上，式(8.26)有近似解.

理想代理OA∞之光子轨迹：η→∞.

η→∞时，观测代理OA(η)趋同于理想代理OA∞，GOR光子运动方程(8.26)约化为牛顿光子运动方程(8.28)，可得精确解，如8.2.3之式(8.5)，光子运动轨迹乃理想的或标准的双曲线.

自然地，η→∞时，基于GOR光子运动方程(8.26)的星光引力偏折角即牛顿偏折角：δN=2GM/(RSc2).

GOR理论之理想观测代理OA∞不存在观测局域性，故其呈现给观测者的是客观真实的光子运动景象，其计算所得星光引力偏折角δN=2GM/(RSc2)是星光掠过太阳表面之客观真实的引力偏折角.

光学代理OA(c)之光子轨迹：η→c.

η=c时，观测代理OA(η)即光学代理OA(c)，GOR光子运动方程(8.26)约化为爱因斯坦光子运动方程(8.30)，可得近似解，如式(8.22)；如式(8.23)所示，光子运动轨迹乃近似的双曲线.

自然地，η=c时，基于GOR光子运动方程(8.26)的星光引力偏折角即爱因斯坦偏折角：δE=4GM/(RSc2).

GOR理论之光学观测代理OA(c)存在观测局域性(c<∞)：其呈现给观测者的并非客观真实的光子运动景象；其计算所得星光引力偏折角δE=4GM/(RSc2)虽然符合光学观测结论，然而，并非星光掠过太阳表面之客观真实的引力偏折角.

一般观测代理OA(η)之光子轨迹：∞>η>c.

(8.32)

如此，因循文献[74]之逻辑路线，采用“逐次逼近法”可求GOR光子运动方程(8.31)之近似解.

不计右端第二项3GMu2/η2，则GOR光子运动方程(8.31)约化为式(8.28)，即牛顿光子运动方程(8.3)，其解即8.2.3之式(8.7)：

(8.33)

其中，e=RSc2/(GM)为牛顿光子轨迹之偏心率.

(8.34)

式(8.34)有解

(8.35)

如图7(c)所示，可设为φ=π+φ(α≥φ≥-α)，其中，α和|φ|皆为小量，cos(π+φ)≈-1，cos 2(π+φ)≈1.鉴于e≫1和η≫c，式(8.35)可近似为

(8.36)

对照或类比式(8.7)可知，式(8.36)为一标准的双曲线.因为式(8.35)乃GOR光子运动方程(8.31)之近似解，式(8.36)乃式(8.35)之近似表达式，所以观测代理OA(η)(η>c)之光子运动方程并非标准的双曲线，如式(8.36)，在GOR理论之光子- 太阳“二体系统”模型中，OA(η)(η>c)之光子运动轨迹乃近似的双曲线.

观察式(8.36)可以发现：η→∞时，GOR光子运动方程之轨道偏心率ê趋同于牛顿光子运动轨道偏心率：→e.自然地，这意味着，η→∞时，GOR光子运动轨迹(式(8.35))趋同于标准的双曲线.

这里，针对光之引力偏折问题，GOR理论之光子运动方程(8.26)，既概括了牛顿光子运动方程(8.3)，也概括了爱因斯坦光子运动方程(8.15).GOR理论又一次将牛顿万有引力论和爱因斯坦广义相对论统一在一起，再一次体现了GOR理论与牛顿万有引力和爱因斯坦广义相对论逻辑上的一致性，以及GOR理论逻辑上的自洽性.

8.4.4 GOR理论之星光引力偏折角

GOR光子运动方程(8.26)表明：对于不同的观测代理，光子运动轨迹将会呈现出不同程度的弯曲，因而，有不同的星光引力偏折角.

现在，牛顿光子运动方程和爱因斯坦光子运动方程皆已成为GOR光子运动方程之特例.

理想代理OA∞之偏折角：η→c.

因循8.2之逻辑路线，求解GOR光子运动方程(8.28)，可得理想代理OA∞之星光引力偏折角：δGOR= 2GM/(RSc2).此即牛顿偏折角δN.

光学代理OA(c)之偏折角：η→∞.

因循8.3之逻辑路线，求解GOR光子运动方程(8.30)，可得光学代理OA(c)之星光引力偏折角：δGOR= 4GM/(RSc2).此即爱因斯坦偏折角δE.

一般观测代理OA(η)之偏折角：∞>η>c.

鉴于GOR光子运动方程(8.31)之解关于η∈(c,∞)的连续性和单调性，其星光引力偏折角δGOR应满足

(8.37)

其中，δGOR=δGOR(η) 依赖于观测代理OA(η)：不同的观测代理必定呈现不同的星光引力偏折角.

如图7(c)所示，光子m由遥远的星星S出发，掠过太阳表面，抵达远离太阳M的地球时，可视其坐标量：r→∞，u→0，φ→π+α，其中，α为一小量.

于是，依式(8.35)，成立：

(8.38)

依式(8.10)，牛顿光子轨道偏心率e=RSc2/(GM)≫1.将偏心率e之值代入式(8.38)，整理后得

(8.39)

如此，GOR理论之星光引力偏折角为

(8.40)

其中：光速c的出现，是作为被观测对象的光子m之速度v=c及其速度矩hK=RSc的体现；而信息波速度η的出现，则是GOR光子运动方程(8.31)中观测代理OA(η)之观测局域性(η<∞)的体现.

式(8.39)(8.40)中，星光引力偏折角δGOR或α只是GOR光子运动方程(8.31)的近似解，要求观测代理OA(η)之信息波速度η满足条件：η≫c.

尽管如此，式(8.40)仍然给予我们如下启示：

1) 星光偏折角δGOR之第一项2GM/(RSc2)独立于观测代理OA(η)，正是牛顿星光引力偏折角δN，代表着客观真实的光之引力偏折.

2) 星光偏折角δGOR之第二项2GM/(RS(3c2+2η2))依赖于观测代理OA(η)，意味着不同观测代理呈现不同程度的光之引力偏折，其中，必定包含着观测效应和表观现象.

3) 观测效应或表观现象乃观测代理OA(η)之观测局域性(η<∞)所致：理想代理OA∞之下，η→∞，则GOR星光引力偏折角δGOR趋同于牛顿之星光引力偏折角δN：δGOR→δN.

依式(8.40)，对于任意观测代理OA(η)(∞>η>c)

(8.41)

式(8.41)意味着，观测代理OA(η)之信息波速度η越大，其呈现给观测者的星光引力偏折角δGOR(η)越小，越接近客观真实的牛顿之星光引力偏折角δN.这一结论与式(8.37)的表述是一致的.

正如本章之前所预计的，GOR理论牛顿星光引力偏折角δN和爱因斯坦星光引力偏折角δE，都只是GOR理论所预测的分属不同观测代理的星光引力偏折角δGOR之特例.

8.5 光之引力偏折：现象与本质

光之引力偏折问题为我们阐明GOR理论，理解观测以及观测媒介或观测代理在物理学理论或模型中所扮演的角色，诠释物理观测和物理实验中的现象与本质，提供了一个范例.

针对光之引力偏折，物理学界无休止地纠结于是爱因斯坦预测正确还是牛顿预测正确.

现在，GOR理论阐明，光之引力偏折，其牛顿预测和爱因斯坦预测源于不同观测代理之理论，基于不同观测代理之视角.爱因斯坦广义相对论所预测的是现象；而牛顿万有引力所预测的则是本质.就现象而言，在光学观测之情景下，爱因斯坦广义相对论之引力偏折预测是正确的，得到光学观测代理OA(c)支持，符合光学观测之现象.然而，就本质而言，在理想观测之情景下，牛顿万有引力论之引力偏折预测是正确的，得到理想观测代理OA∞支持，符合客观物理世界真实的星光引力偏折景象.

不同视角，不同现象.然而，本质是不变的.

8.5.1 伽利略- 牛顿视角

正如OR和GOR理论反复强调的，伽利略- 牛顿理论乃理想观测理论，是客观物理世界的真实写照.

OR和GOR理论已经阐明，伽利略-牛顿理论隐喻着理想观测条件，归属理想观测代理OA∞.如8.2.1所述，理想代理OA∞将观测条件极度地理想化：信息波速度无穷大，观测信息的传递无须时间，无相对论性效应；信息子动量无穷小，不会对被观测对象之运动构成扰动，无量子效应.

只有在如此理想化的观测条件下，自然世界才会呈现出其客观真实的本来面貌，虽然，这种极度理想化的观测条件是“可欲而不可求”的.

理想观测代理OA∞可谓“伽利略- 牛顿视角”.

制约于观测代理之局域性，人类永远也无法感知或观测到完全客观真实的物理世界.然而，我们的理性可以触及它.

正是因为理想代理OA∞之信息波速度无穷大，伽利略- 牛顿理论无相对论性效应；正是因为理想代理OA∞之信息子动量无穷小，伽利略- 牛顿理论无量子效应.基于理想代理OA∞，伽利略- 牛顿之理论得以触及客观真实的物理世界.

在行星- 恒星“二体问题”中，被观测对象是行星.相对于行星的质量，一般观测代理之信息子质量极小，不会对行星运动产生显著影响.因此，行星- 恒星“二体问题”无须讨论观测代理之信息子动量问题.而光子- 太阳“二体问题”中，被观测对象是光子.光子质量极小，其运动易受信息子扰动而呈现量子效应.因而，光子- 太阳“二体问题”不得不涉及观测代理之信息子动量问题.幸而，理想代理OA∞隐喻着信息子动量无穷小的理想化条件或理想化假设.

可见，基于理想代理OA∞观测光子运动，恰如我们借助光观看鸟或飞机在天空中飞行.就光之引力偏折问题而言，理想代理OA∞呈现给观测者的光子运动轨迹乃客观真实的光子运动轨迹，换句话说，基于牛顿万有引力论的星光偏折预测，代表着星光掠过太阳表面之客观真实的景象.

如此，牛顿光子运动方程(8.3)计算得出的星光引力偏折角δN=2GM/(RSc2)，是客观真实的星光引力偏折角.

8.5.2 爱因斯坦视角

正如OR和GOR理论反复强调的，爱因斯坦相对论乃光学观测理论，其相对论性效应乃观测效应.

正如8.3.1所述，爱因斯坦广义相对论隐喻着光学观测条件，归属光学观测代理OA(c)：信息波即光波，信息波速度即光速c，存在观测局域性(c<∞)，观测信息的传递需要时间，呈现相对论性效应；信息子即光子，信息子动量即光子动量，可能对被观测之微观粒子的运动构成扰动，呈现量子效应.

光学观测代理OA(c)可谓“爱因斯坦视角”.

爱因斯坦并未十分清楚地意识到，自己的理论是一个局部理论(partial theory)：光学观测理论，仅当观测代理OA(η)即光学代理OA(c)时方能成立；更未意识到，光学观测存在观测局域性(c<∞)，并且，这种观测局域性乃相对论性效应的根源和本质.

就光之引力偏折问题而言，爱因斯坦广义相对论基于光学代理OA(c)观测光之引力偏折，其中，光子既是OA(c)之被观测对象又是OA(c)之信息子：光子m之运动信息的携带和传递依赖于光子m自身.因此，如图7(c)所示，光学代理OA(c)无法观测到光子m真实的运动轨迹，仅当光子m其抵达我们的视网膜或观测器时，我们才能感知其存在，并将其虚幻映像(点B)作为光源或光源所在方向.

正如8.3所阐明的，光学代理OA(c)之观测局域性(c<∞)的存在，导致OA(c)呈现观测效应和表观现象：爱因斯坦光子运动方程(8.15)计算所得星光引力偏折角δE=4GM/(RSc2)，乃光学代理OA(c)呈现给观测者的星光引力偏折角，并非完全客观真实的光之引力偏折.然而，就现象而言，爱因斯坦广义相对论做出的光之引力偏折预测，符合光学观测，与光学代理OA(c)所呈现的光之引力偏折现象是一致的，得到日全食之光学观测的支持.

实际上，无论是爱丁顿或戴森的日全食观测[75-76]，还是美国怀俄明州的日全食观测[78]，皆为借助于光学代理OA(c)的光学观测，其所呈现的星光引力偏折现象自然支持爱因斯坦广义相对论之预测.

8.5.3 GOR视角

人类感知客观世界，必须借助于一定的观测媒介或观测代理.现实之一切观测代理OA(η)皆存在观测局域性(η<∞)，其呈现给观测者的，只能是客观世界的某种映像；我们永远无法观测到完全真实的客观世界.不同观测代理，呈现给观测者不同的映像.

然而，客观真实的物理世界是唯一的！

OR和GOR理论已经阐明，理论上，一切物质运动形式皆可为观测媒介，为观测者传递被观测对象之信息.GOR理论中，光学代理不再具有特殊地位：光并非人类唯一可加以利用的观测媒介.

如此，观测者可以基于更为广阔的视角，观测自然世界.这便是所谓的“GOR视角”.

针对光子引力偏折问题，GOR理论基于GOR场方程和GOR运动方程建立了GOR光子- 太阳“二体系统”模型，即GOR光子运动方程(8.26)，概括统一了牛顿光子运动方程(8.3)和爱因斯坦光子运动方程(8.15).GOR光子运动方程乃一般观测代理OA(η)(η∈ [c,+∞))之光子运动方程，自然地，依赖于OA(η)及其信息波速度η，包含着OA(η)之观测效应.仅当η→∞时，GOR光子运动方程(8.26)约化为牛顿光子运动方程(8.3)，独立于观测代理OA(η)及其信息波之速度η.这时的GOR光子运动方程，即牛顿光子运动方程，描绘了客观真实的星光引力偏折轨迹.

自然地，GOR光子运动方程计算所得星光引力偏折角δGOR=δGOR(η)依赖于观测代理OA(η)及其信息波速度η.如8.4之计算和分析：η→c时δGOR(η)=δE，此即爱因斯坦偏折角；η越大，OA(η)越接近理想代理OA∞，而δGOR(η)越接近牛顿偏折角δN；η→∞时δGOR(η)=δN，此即客观真实的星光引力偏折角.

GOR理论阐明：爱因斯坦广义相对论之预言，虽与光学观测现象相符，却并不等同客观真实之物理现实；反之，牛顿万有引力论之预言，虽与光学观测现象不符，却代表着客观真实的物理存在.

基于GOR视角，我们终于发现：观测的，即现象的或表象的，未必本质的或客观真实的.

9 GOR理论与光之引力红移

本章围绕爱因斯坦著名的三大预测之一——光之引力红移(引力场中光或光子频率衰减)问题，继续解析和测试GOR理论.

GOR理论力求基于PGC原理，类比爱因斯坦广义相对论探究光之引力红移现象的逻辑路线，同时，基于“时频比不变性”，演绎光之引力红移方程.GOR理论将基于能量守恒原理定义引力红移，探究不同观测代理之下光子的引力红移问题，以及不同观测代理之下信息子的引力红移问题.特别地，GOR理论将对牛顿万有引力论和经典力学的引力红移方程进行新的论述和新的演绎.

GOR引力红移方程，与GOR理论之一切方程式一样，具有高度的一般性和概括性，将牛顿引力红移方程和爱因斯坦引力红移方程统一起来，同时，为牛顿引力红移和爱因斯坦引力红移注入新的见解.

9.1 关于光之引力红移

与光之引力偏折预测一样，原本，光之“引力红移”预测乃爱因斯坦为测试和检验其广义相对论著名的三大预言之一，是爱因斯坦基于其广义相对论重要逻辑前提之“等效原理”提出的.

光之引力红移，意即：引力时空中，光或光子的频率会随其引力势的变化而变化.当然，引力场中的光或光子不仅仅会“红移”，也会“蓝移”.

如图8(a)①②所示，一艘宇宙飞船在太空中航行，飞船尾部光源向飞船前端发射频率为f的光或光子，飞船前端宇航员观测到光或光子的频率为fO.可以判断：飞船匀速(a=0)时，fO为光或光子辐射频率，即fO=f；而飞船加速(a>0)时，fO则小于光或光子辐射频率，即fO

图8 等效原理与引力红移Fig.8 Pinciple of equivalence and gravitational redshift

根据爱因斯坦之“等效原理”，惯性力与引力等效，惯性力场与引力场等效；宇航舱内的宇航员不能确定飞船处于加速(a)状态或处于重力场(g=-a)状态.如图8(b)①所示，设宇航员处于某星球(重力场：g=-a)地表上方，地表光源垂直向上辐射频率为f的光或光子，而宇航员观测到光或光子之频率为fO.根据“等效原理”，爱因斯坦预测：等效于宇航员在宇航舱内的观测情形(见图8(a)②)，fO

此即光之引力红移.

反之，如图8(a)③④所示，飞船前端光源向飞船尾部发射频率为f的光或光子，飞船尾部宇航员观测到光或光子的频率为fO.可以判断：飞船匀速(a=0)时，fO为光或光子发射频率，即fO=f；而飞船加速(a>0)时，fO则大于光或光子发射频率，即fO>f(光之“蓝移”).类似地，如图8(b)②所示，设宇航员处于某星球(重力场：g=-a)地表，地表上方光源垂直向下辐射频率为f的光或光子，而宇航员观测到光或光子之频率为fO；如此，根据“等效原理”可预测：等效于宇航员在宇航舱内的观测情形(见图8(a)④)：fO>f(光之引力蓝移).

与光之引力偏折不同，光之引力红移通常基于引力场之“时间膨胀”诠释，而非爱因斯坦广义论之“时空弯曲”说.正是基于引力场中观测者之观测时间的“膨胀”，爱因斯坦广义相对论得以对光之引力红移进行计算并做出预测.实际上，爱因斯坦广义相对论中，光之引力红移和引力时空之“时间膨胀”被视为等效的物理效应[79-81].

测试或验证光之引力红移，最简单易行的是地球观测者观测来自太阳的光谱.太阳向地球辐射光，假定太阳光在太阳表面时频率为f，而当其抵达地球时地球观测者之观测频率为fO.无论基于爱因斯坦之引力红移预测还是基于牛顿之引力红移预测，太阳光来到地球必定会“红移”：fO

爱因斯坦基于“等效原理”的光之引力红移预测是定性的.在其广义相对论正式建立之前，爱因斯坦无法对光之引力红移进行定量的计算和定量的预测.广义相对论正式建立之后，爱因斯坦利用广义相对论场方程求得时空度规gμν，进而基于光子时空线元方程：ds=gμνdxμdxν，以及广义相对论之时空变换因子γ=dt/dτ，导出太阳光谱之引力红移公式，同时，计算得出太阳光谱引力红移之理论值

(9.1)

式中：G为万有引力常数；MS为太阳质量；RS为太阳半径；DSE为太阳地球之距离；g00(r)为距太阳中心r处之度规00(元素)；ZE为爱因斯坦之相对频移量(ZE<0时意味着“红移”)；Δf为绝对频移量；f为参考频率(或理论值或观测值，或发射值或接收值).

Adam[82](1959年)给出了太阳光谱红移之实际观测值：Z=-2×10-6.Blamont和Roddier[83](1961年)以及Brault[84](1963年)给出的太阳光谱红移之实际观测值：Z=-2.12×10-6，在精度5%范围内符合爱因斯坦广义相对论之理论值.

对于太阳的实际观测及其光谱分析似乎是支持爱因斯坦广义相对论之引力红移预测的.但也有观点[74]认为：式(9.1)之红移量极小，太阳色球湍流(turbulence in chromosphere)和斯塔克效应(Stark effect)可能对其度量的准确性产生不确定性影响.

除太阳之外，其他恒星的光谱也可用于测试爱因斯坦广义相对论之引力红移预测；特别地，高密度恒星可呈现出较之太阳更为显著的引力红移.

1954年，Popper[85]观测波江座40伴星(40 Eridani B)所得之光谱红移量：Z=-5.6×10-5，而基于爱因斯坦广义相对论的理论值则为ZE=-7×10-5；1971年，Greenstein等[86]观测天狼星伴星(Sirius B)所得其光谱红移量：Z=-(3.00±0.05)×10-4，而基于爱因斯坦广义相对论的理论值则为ZE=-(2.8±1.0)× 10-4.这些观测大体上与爱因斯坦之引力红移预测相符.然而，这些恒星距离地球遥远，其质量和半径难以准确测定，其引力红移之观测的准确性存疑.

1958，Mössbauer[87]发现穆斯堡尔现效应(Mössbauer effect，即原子核辐射的无反冲共振吸收效应)，其能量分辨率可高达10-13，为引力红移的精确测定以及在地球表面进行引力红移实验创造了条件，可测定地球表面高度差ΔH仅20 m的引力红移量.

设想地球表面一光信号发生器自下而上(自上而下)地辐射频率为f的光或光子，距离地表ΔH>0(<0)之处的穆斯堡尔效应观测器接收来自地表的光信号，接收频率为fO，频率差：Δf=fO-f.

依照爱因斯坦广义相对论：

(9.2)

式中：ZE即爱因斯坦相对频移量(ZE<0时意味着“红移”)；ME为地球质量；RE为地球半径；ΔH为观测器距离光源之高度差；g00(RE)乃地表之度规00(元素g00)，而g00(RE+ΔH)则为距离地表ΔH之处的度规00(元素g00)；g乃地表重力加速度.

较硬的光或光子可以获得更好的穆斯堡尔效应和更显著的引力红移，如57Fe原子核伽马射线.

1960年，Pound和Rebka[88]以57Fe原子核之伽马射线作为辐射源，设置ΔH=22.5 m，观测其引力红移.根据式(9.2)计算所得理论值ZE=-2.46×10-15.ZE虽然极小，仍可利用穆斯堡尔效应测定.Pound和Rebka的实际观测值Z=-(2.57±0.26)×10-15：Z与理论值ZE之比Z/ZE=1.05±0.10；Z在10%的精度范围内与爱因斯坦广义相对论之理论值ZE相符.

1964年，Pound和Snider[89]重复了1960年的实验，提高了观测精度，其观测值Z与理论值ZE之比Z/ZE= 0.990±0.007 60：实际观测值Z在1%的精度范围内与爱因斯坦广义相对论之理论值ZE相符.

总之，光之引力红移的观测和实验与爱因斯坦广义相对论的理论计算和预测是一致的.

然而，与光之引力偏折的情形不同，爱因斯坦之引力红移预测似乎失去挑战和竞争的对手——牛顿万有引力论也能预测光之引力红移，而且，其结论似乎与爱因斯坦广义相对论相同或相似，不具有观测上的可分辨性.

牛顿之引力红移预测无须“等效原理”或引力场“时间膨胀”.牛顿之引力红移预测基于物理学最简明的原理——能量守恒原理：光之频率意味着光之能量；光之能量的损耗必定导致光之频率红移.根据能量守恒原理，基于牛顿万有引力论和经典力学计算光之引力红移，需要计算光子在引力场中的势能，因而，需要光子之经典质量，特别地，涉及光子之“引力质量”.依照爱因斯坦相对论，光子无“静止质量”；实际上，这意味着光子无经典质量或引力质量.没有光子引力质量，牛顿万有引力论和经典力学难以对光之引力红移进行理论计算和定量预测.

现行的牛顿引力红移公式，将爱因斯坦之“相对论性质量”(retlativistic mass)作为牛顿之“引力质量”(gravtitational mass)，进而，计算光子之势能差ΔV，演绎“伪牛顿引力红移方程”：

(9.3)

式中：ZPN乃“伪牛顿引力红移方程”之引力频移量(ZPN<0时意味着“红移”)；E=mc2可视为光子“固有能量”(光子在真空中的能量)；m为光子之相对论性质量(既是光子之相对论性“惯性质量”也是光子之相对论性“引力质量”)；ΔE为光子从发射到接收过程中能量之增量；V为光子发射时的势能；VO则为光子被观测器接收时的势能.

假定式(9.3)中作为光子引力质量的m是不变的，则光子之势能差ΔV及其引力红移量ZPN可计算.

对于式(9.1)之日地引力红移观测之情形，采用式(9.3)，即可基于牛顿引力论和经典力学计算太阳光波谱之“绝对红移量”ΔE和“相对红移量”ZPN=ΔE/E：

(9.4)

对于式(9.2)之地面引力红移观测之情形，采用式(9.3)可得57Fe原子核伽马射线谱之“绝对红移量”ΔE和“相对红移量”ZPN=ΔE/E：

(9.5)

对照式(9.4)(9.5)和式(9.1)(9.2)可知，就太阳光谱之引力红移现象的观测而言，牛顿引力红移预测与爱因斯坦引力红移预测是相似的：ZPN≈ZE，其差异在观测上难以分辨.如此，人们好奇的不再是牛顿和爱因斯坦究竟谁的预言更正确；而是关于光之引力红移，为什么牛顿万有引力论之预测与爱因斯坦广义相对论之预测会是相近的呢！

特别需要指出：如式(9.3)所示，现行的“牛顿引力红移公式”，不仅借用了爱因斯坦公式E=mc2，涉及相对论；而且，借用了普朗克方程E=hf，涉及量子论.由此可见，现行的牛顿引力红移公式，并非纯粹的牛顿万有引力论和经典力学之产物，而是经典力学与相对论和量子论的混合体.

稍后，我们将演绎出纯粹基于经典力学的牛顿引力红移方程，并且将其纳入GOR理论体系.

9.2 爱因斯坦广义相对论与光之引力红移

爱因斯坦光之引力红移预言，与其光之引力偏折一样，是基于其“等效原理”提出的.

广义相对论正式建立之前，爱因斯坦只能运用其构思的“等效原理”，以图8所示的方式和逻辑，定性地阐述其光之引力红移，无法对光之引力红移做出定量计算和定量预测.广义相对论正式建立之后，爱因斯坦基于广义相对论之场方程近似解(第6章6.2.1之式(6.3))，导出光之引力红移公式，计算得出太阳光谱引力红移的理论值，为验证爱因斯坦广义相对论及其光之引力红移预言提供了依据.

探究光之引力红移问题，开展光之引力红移的观测和实验，其意义在于：验证爱因斯坦“等效原理”，检验爱因斯坦广义相对论，测试引力时空之“时间膨胀”或“势钟慢”效应.

重温爱因斯坦光之引力红移的预言及其基于广义相对论的理论计算，将为我们基于GOR理论探究光之引力红移问题提供参照和类比，同时，有助于我们进一步理解和认识GOR理论.

9.2.1 爱因斯坦光之引力红移方程

爱因斯坦演绎其引力红移方程，并非直接计算光或光子在引力时空之运动过程中的频移量，而是基于光之“引力频移”与引力时空之“时间膨胀”的等效性，间接地推论和计算光之引力红移.

理想化的球对称静态时空——

如图9所示，星球M作为引力源，理想化地形成一球对称引力时空，满足理想化的“静态时空”(static spacetime)条件：

(9.6)

式中：第一项是“稳态时空”(stationary spacetime)条件，意味着时空度规gμν不随时间变化；第二项为“正交时空”(orthogonal spacetime)条件.

图9 球对称引力时空的光之红移Fig.9 Redshift of light in spherically sysmmetric gravitational spacetime

满足式(9.6)中2项条件的引力时空谓之“静态时空”.爱因斯坦场方程近似解(第6章6.2.1式(6.3))和Schwarzschild精确解(第6章6.2.2式(6.7))之引力时空度规皆球对称静态时空度规，皆可用于演绎球对称引力时空之引力红移方程.

爱因斯坦引力红移方程的演绎——

依照爱因斯坦广义相对论之逻辑(参见文献[90])，如图9所示，设：以星球M为引力源和引力中心的引力时空中，静止于点A(距离引力中心rA)的光源(光钟)T向远处点B(距离引力中心rB)发射光信号：T在坐标时刻t1发射频率为fA(t1)的光信号，点B之观测者在坐标时刻t2接收到这一光信号，接收频率为fB(t2)；T在坐标时刻t′1又向点B发射频率为fA(t′1)的光信号，点B之观测者在坐标时刻t′2接收到这一光信号，接收频率为fB(t′2).

根据式(9.6)之理想化条件，M之引力场乃“稳态时空”，不随时间变化.若光源(光钟)T在时刻t1和t′1发射的光信号频率是相同的：fA(t1)=fA(t′1)=fA，则点B之观测者在时刻t2和t′2接收到2个光信号的频率也应该是相同的：fB(t2)=fB(t′2)=fB.并且，2个光信号由点A传递至点B的时间间隔也应该是相同的：

t2-t1=t′2-t′1

或

t′1-t1=t′2-t2
(t′1-t1≡dtA,t′2-t2≡dtB)

(9.7)

式(9.7)意味着：T在点A发射的2个光信号之时间差等于点B接收到2个光信号的时间差：dtA=dtB.

依文献[90]：“t是坐标时间，不是观测者实际测得的固有时间τ.”并且，文献[90]认为点A和点B之观测者所经历的“固有时间”分别为dτA和dτB，应该是不同的.依爱因斯坦广义相对论之时空变换因子γ=dt/dτ(第3章3.2.4之式(3.11))，成立：

(9.8)

式中：如图9所示，g00(rA)和g00(rB)分别为M之球对称时空中点A和点B时空度规之00(元素).

式(9.8)意味着：dτA≠dτB或dτA>dτB.此即引力时空之“时间膨胀”现象或“势钟慢”效应.

依文献[90]所述：对于“势钟慢”效应，爱因斯坦建议用光谱频移(“红移”或“蓝移”)来检验；原子辐射光谱固有频率反映原子固有振荡频率：f=dN/dτ，式中N为原子内部固有振荡次数.M之引力时空中，点A和点B之观测者所得原子之振荡次数相同(dNB=dNA)时，由公式f=dN/dτ可知

(9.9)

将式(9.9)代入式(9.8)即可获得

(9.10)

式中：G为万有引力常数；M为星球质量；rA为静止于点A的光源(光钟)T到引力中心之距离；rB为点B到引力中心之距离.

此即爱因斯坦引力红移方程，等同式(9.1).

测试光之引力红移，最简单易行的是观测太阳或其他恒星之光谱的引力红移；而相应的理论计算即可依据式(9.10)：设M=MS为太阳，点A位于太阳表面(rA=RS)；rB→∞时g00(rB)→1.将Schwarzschild度规g00(r)=1+2GM/(rc2)代入式(9.10)可得

(9.11)

此即自由时空观测者观测太阳光谱之理论上的引力红移量.若设B为地球，因为日地距离远大于太阳半径：rB≫RS，所以地球上的观测者观测太阳光谱所得引力红移必定近似式(9.11)：ZE≈-2.12×10-6.

9.2.2 时频比不变性与光之引力红移

爱因斯坦光之引力红移方程(9.10)及其演绎过程存在一些疑点，值得我们思考或探究.

根据OR和GOR理论(第3章之3.3)，“固有时间”dτ是客观真实的时间，不依赖于观测者，本质上而非数学之形式上，也不依赖于观测代理.我们不能理解，式(9.8)之同一观测代理中不同观测者之“固有时间”dτA和dτB为什么是不同的.反过来，我们不能理解，式(9.9)中不同观测者之“原子振荡次数”dNA和dNB为什么是相同的.爱因斯坦光之引力红移方程的演绎，逻辑上并不十分清晰明确.

根据OR和GOR理论：dτA=dτB=dτ.因此，基于广义相对论时空变换因子：γ=dt/dτ(第3章3.2.4之式(3.11))，式(9.8)需变更为

故

(9.12)

OR和GOR理论有一重要原理(第3章3.3之式(3.17))：“时频比不变性”，乃时间t和时钟频率f重要的关系式.依“时频比不变性”，成立：

(9.13)

其中，特别注意，dtA和dtB皆可视为光钟T之观测时间，fA和fB皆可视为光钟T之观测频率.

由此即可导出爱因斯坦光之引力红移方程

(9.14)

式(9.14)与爱因斯坦导出的光之引力红移方程(9.10)是相同的.然而，式(9.14)源于OR和GOR理论之“时频比不变性”，逻辑清晰简洁.

这一结果从一个侧面印证了OR和GOR理论之“时频比不变性原理”.实际上，它是一个定理.

9.2.3 光学观测体系之引力红移

根据OR和GOR理论，爱因斯坦广义相对论是光学观测之理论，其观测代理乃光学代理OA(c)——为观测者传递观测信息(包括引力红移信息)的观测媒介或“信息波”是光或电磁相互作用.

观察图9我们也会产生些许疑惑.

就爱因斯坦广义相对论而言，水星进动问题之中，被观测对象是水星，为观测者传递水星运动信息的是光；而光之引力偏折问题中，被观测对象则是光子，为观测者传递光子运动信息的是光子自身.那么，光之引力红移问题中，被观测对象是什么呢？是运动的光，还是静止的光源(光钟)T？

特别值得注意：爱因斯坦引力红移方程，无论式(9.10)还是式(9.14)，其演绎过程皆利用了时空变换因子γ=dt/dτ=1/√(g00).然而，爱因斯坦广义相对论之时空变换因子的一般表达式为γ=1/√((√(g00)-γivi/c)2-v2/c2)(第3章3.2.4之式(3.16)).在式(9.6)之“时空正交”条件下，γi=0；因而，γ=1/√(g00-v2/c2)(第3章3.2.4之式(3.12)).无论式(3.16)还是式(3.12)，γ=1/√(g00)要求被观测对象静止于引力时空：v=0.

由此可见，图9所示的光之引力红移问题中，被观测对象绝非光或光子，而只能是静止于点A发射光信号的光源(光钟)T，而T发射的光或光子则只是爱因斯坦光学代理OA(c)之观测媒介，是OA(c)传递T之信息的“信息波”或“信息子”.

需要说明的是：依照时空变换因子(3.16)，v=0时，无须“时空正交”条件(gi0=0 (i=1,2,3)).

其次，存在的另一问题是：图9中作为引力红移之被观测对象的T必须是光源或光钟吗？

实际上，如前所述，爱因斯坦光之引力红移方程并非直接计算光之频移，而是基于光之“引力频移”与引力时空之“时间膨胀”的等效性，间接地推论和计算光之引力红移.无论式(9.10)还是式(9.14)，所谓光之引力红移Δf或ZE=Δf/f，实际上，是时空变换因子γ=dt/dτ之引力场的“时间膨胀”：γ=dt/dτ意味着“引力时间”的“膨胀”.

式(9.11)极为直观地显示了光之引力红移ZE与时空变换因子的关系：ZE=1-γ.换句话说，自由时空之观测者观测太阳光谱，其光之引力红移ZE即太阳引力场之“时间频移”或“时间膨胀”：

(9.15)

式中dt即太阳之球对称引力场中的“引力时间”，或者说，即引力时空之“观测时间”.

由此可见，图9中的T是静止于星球M之引力时空或星球表面的“势钟”.

理论上，一切波或周期性物理现象皆可定义钟或时间.依照德布罗意物质波论，一切物质粒子或物质体系皆物质波，因而，皆可用于定义钟或时间.如此，作为引力红移之被观测对象的时钟，T可为任意物质体系或任意周期性物理现象.

然而，无论如何，在爱因斯坦广义相对论中，为观测者传递T之信息的是光学代理OA(c).因此，图9中，T从点A向点B发射的信号必定是光或光子，但不是作为被观测对象，而是OA(c)的观测媒介——OA(c)之“信息波”和“信息子”，携带着T之信息，包括其时间信息和空间信息，同时，包含了光学代理OA(c)之观测局域性(c<∞)所致的观测效应.

至此，可以得出结论：爱因斯坦光之引力红移方程是光学代理OA(c)之“信息波”和“信息子”的引力红移方程；爱因斯坦光之引力红移理论，是光学观测代理OA(c)之引力红移理论.爱因斯坦光之引力红移方程(9.10)中，ZE是光学代理OA(c)之引力红移，代表着整个光学观测体系的引力红移：既是OA(c)之“信息波”和“信息子”的引力红移，也是OA(c)之时间的引力红移，乃至一切物质体系之德波罗意物质波的引力红移.

9.3 牛顿万有引力论与光之引力红移

牛顿万有引力论也能解释光之引力红移.

然而，与爱因斯坦广义相对论不同，牛顿万有引力论诠释光之引力红移无须“等效原理”，无须引力场之“时间膨胀”或“势钟慢”效应.

实际上，如本章9.1所述，光之引力红移并不意味着引力时空之“时间膨胀”，也非“势钟慢”效应.引力红移的本质是能量之形式的转化.牛顿的光之引力红移理论，其理论基础乃物理学最简明的原理：能量守恒原理.

9.3.1 伪牛顿光之引力红移方程

牛顿万有引力论基于能量守恒原理计算光之引力红移，需要计算光子在引力场中的经典动能K和经典势能V，需要光子之经典质量m∞：K需要经典惯性质量mi；V需要经典引力质量mg.

然而，牛顿力学或经典力学并无关于光子经典质量的知识或信息.于是，现行策略只得借用爱因斯坦相对论中光子的相对论性质量m(=E/c2=hf/c2)作为经典力学之经典质量，演绎所谓“牛顿红移方程”.

以下演绎过程源于文献[90]，现行所谓牛顿光之引力红移方程的推演大抵如此.(然而，我们不能确定，这一途径或策略是否始于爱因斯坦.)

如图9所示，光子由M之球对称静态时空之点A飞向点B；依经典力学，光子能量的损耗应为

(9.16)

式中：G为万有引力常数；M为引力时空之引力源质量；mg则为光子引力质量.

若光子引力质量mg等同于光子惯性mi质量，并且假定光子质量在运动过程中无损耗，则

(9.17)

值得注意，文献[90]特别列出了如下关系式：

(9.18)

其中，爱因斯坦公式E=mc2中的相对论性质量m，既被作为光子之“惯性质量”mi又被作为光子之“引力质量”mg，代入式(9.17)，得光子之绝对红移量

(9.19)

而光子之相对红移量ZPN则为

(9.20)

正如本章9.1所述，现行所谓“牛顿引力红移方程”(式(9.20))，其演绎过程既借用了爱因斯坦公式E=mc2又借用了普朗克方程E=hf；既涉及相对论又涉及量子论.这意味着，现行牛顿光之引力红移方程并非纯粹经典力学的产物，而是经典力学与相对论和量子论的混合体，可谓“伪牛顿光之引力红移方程”.

一般地，GM/(rc2)(≪1)乃一小量，观察和对照爱因斯坦光之引力红移方程(9.14)中的ZE可知

(9.21)

可见，伪牛顿引力红移方程式(9.20)与爱因斯坦引力红移方程(9.14)似乎是“相似”的.产生这种相似性的原因或许正因为：它是“伪牛顿”的！

我们期待真实的牛顿引力红移理论，真正基于牛顿万有引力论和经典力学演绎牛顿引力红移方程.

9.3.2 光子静止质量和光子经典质量

OR理论[1-3]已经阐明：牛顿万有引力论和经典力学归属理想代理OA∞；爱因斯坦相对论归属光学代理OA(c).因此，爱因斯坦之引力红移理论基于OA(c)之“相对论性物理量”；而牛顿之引力红移理论则应基于OA∞之“经典物理量”.

无论“相对论性物理量”或“经典物理量”，除了时间之外，质量必定是其中最基本的物理量.基于牛顿万有引力论和经典力学演绎牛顿光之引力红移方程，自然地，需要光子的“经典质量”.物质粒子的“经典质量”m∞是理想代理OA∞之观测质量.根据第1章之定义1.2，m∞既是物质粒子客观真实的“固有质量”又是物质粒子之“静止质量”mo.

经典质量即静止质量——

原本，“经典质量”指经典力学之物质质量；而“静止质量”则是爱因斯坦狭义相对论的产物.

设有物质粒子或物质体系m，其观测代理OA(η)之观测质量为m(η)；若η→∞，则OA(η)趋同于理想代理OA∞，m(η)趋同于“经典质量”m∞.如此，根据OR理论之“质速关系”式(1.16)，成立：

(9.22)

可见，“经典质量”即“静止质量”：m∞=mo.

根据OR和GOR理论，物质粒子或物质体系，其“固有质量”即客观真实的质量，具有客观真实的惯性特性和引力特性：m∞=mi=mg=mo.

这意味着，牛顿光之引力红移理论和牛顿光之引力红移方程的演绎，依赖于光子“静止质量”.

那么，光子有“静止质量”吗？如果光子有“静止质量”，那么，一粒光子到底有多重呢？

光子有静止质量吗？

爱因斯坦狭义相对论告诉人们，光子无“静止质量”，这也就意味着光子无“经典质量”，有悖于人类朴素的自然观.

熟悉爱因斯坦狭义相对论的都知道，洛伦兹变换中有一个“洛伦兹奇点”：被观测对象之速度v达到光速c时，洛伦兹因子γ达到无穷：γ=1/√(1-v2/c2) →∞.因而，在洛伦兹奇点处，被观测对象之相对论性质量m=γmo=∞，除非，其“静止质量”mo为零.

于是，在狭义相对论中，光子的“静止质量”mo被爱因斯坦强行地设置为零.观测和实验似乎也相当地配合：光子“静止质量”至今未能被观测和实验探测到，而上限值却越来越小[91-94].2014年，PDG粒子数据组推荐的光子质量上限为1.5×10-54kg[95].(其实，人们早已观测到了光子的“静止质量”，只是没能意识到，那就是光子之“静止质量”.1919年，爱丁顿通过观测日全食，发现星光掠过太阳时，其轨迹出现了偏折或弯曲，由此肯定道：“光也有重量”.)

OR理论[1-3]已经从理论上阐明，光子，乃至一切物质粒子或物质体系皆具有其“静止质量”.

关于光子“静止质量”问题，OR理论有详尽的论述[1-3].简而言之：并非光子无静止质量.就光子之“相对论性质量”m和“静止质量”mo而言，套用霍金的话说，洛伦兹变换和狭义相对论之“质速关系”在洛伦兹奇点处失效了[13].实际上，无论是数学模型之奇点，还是观测或实验，其光子零质量的结论，都只是光学代理OA(c)之观测局域性(c<∞)的表现：不能用光子去探测光子自身的质量！或者说，光子之“静止质量”无法通过光学代理OA(c)来测定！

正如OR理论[1-3]已经阐明的：如果我们能借助超光速观测代理OA(η)(η>c)观测光子，那么，我们将会发现，原来，光子是拥有“静止质量”的——根据OR理论之“质速关系”式(1.16)，成立：

(9.23)

如此，可以明确：光子，乃至一切物质粒子，皆具有“静止质量”mo.并且，正如第3章之“3.6 一切相对论性效应皆观测效应”所阐明的：相对论性质量m=Γ(η)mo=Γ∞mo+ΔΓ(η)mo(Γ∞≡1)依赖于观测代理OA(η)，其中，只有“静止质量”mo是客观真实的质量，而ΔΓ(η)mo纯属观测效应；物质粒子客观真实的惯性特性和引力特性取决于“静止质量”mo.

明确了光子具有“静止质量”mo，便明确了光子具有“经典质量”m∞，即可基于牛顿万有引力论和经典力学计算光子之经典动能K和经典势能V：

(9.24)

进而，可演绎真实的牛顿光之引力红移方程.

一粒光子究竟有多重？

尽管爱因斯坦认为光子无“静止质量”，源于内秉的自然观，人们潜意识里不愿意接受光子零质量的假设或推论.许多物理学家，甚至包括伟大的德布罗意[96-97]、薛定谔[98-99]、费曼[100]，仍然不惜耗费时光，力求探测光子之“静止质量”.

OR理论明确了光子具有“静止质量”.或许，基于OR理论之关系式，特别是其“质速关系”(式(1.16))以及“质能关系”E=mη2，结合观测实验，我们可以推测或确定光子的“静止质量”.

普朗克的黑体辐射实验[43]，其黑体辐射腔相对于实验室和观测者是静止的.有鉴于此，OR理论曾将黑体辐射实验视为理想观测代理OA∞之实验，将E=hf视为光子经典动能：hf=moc2/2，进而推测频率为f的光子之“静止质量”[2]：mo=2hf/c2.

然而，这一推测存在诸多疑点.

实际上，黑体辐射实验之被观测对象是光子，为观测者或观测器传递光子信息的也是光子：光子自身即“信息子”.这意味着，黑体辐射实验之观测代理是光学代理OA(c).质能关系E=mc2是爱因斯坦狭义相对论之关系式，归属于光学代理OA(c).对于光子，人们普遍认可：E=mc2=hf，这意味着，爱因斯坦公式E=mc2和普朗克方程E=hf同属光学代理OA(c).因此，光学代理OA(c)之普朗克光子能量E=hf，并不等同于理想代理OA∞之光子经典动能：E≠moc2/2.

对于光子，爱因斯坦公式E=mc2和普朗克方程E=hf中的光子能量E即光子之动能K.

因此，基于能量的观点和能量守恒原理，光之引力红移可等价地定义为

(9.25)

式中：f和Δf分别为光学代理OA(c)之相对论性的光子频率及其增量；K和ΔK分别为光学代理OA(c)之相对论性的光子动能及其增量；V和ΔV分别为光学代理OA(c)之相对论性的光子势能及其增量.

式(9.25)意味着，基于光子频率的爱因斯坦光之引力红移定义：ZE=Δf/f，等价于基于光子动能的爱因斯坦引力红移定义：ZE=ΔK/K.

OR理论确认光子具有“静止质量”mo，如此，根据爱因斯坦狭义相对论，可计算光子在引力时空中的OA(c)相对论性动能和OA(c)相对论性势能：

(9.26)

其中，γ=1/√(1+2χ/c2-v2/c2)为爱因斯坦广义相对论之时空变换因子(第3章式(3.12))，m和mo分别为光子之相对论性质量和静止质量，Kr和Vr分别为光子距离引力中心r时的相对论性动能和相对论性势能，而KF=mc2则为光子在真空或自由时空SF中的相对论性动能，即光子的OA(c)总能量：KF=E=Kr+Vr.

针对图9所描述的光之引力红移场景：ΔV=VB-VA，根据式(9.25)和式(9.26)，成立：

(9.27)

式中：KB为光子距离引力中心rB时OA(c)的相对论性动能；VA和VB分别为光子距离引力中心rA和rB时OA(c)的相对论势能；g00(rA)和g00(rB)分别为OA(c)之引力时空点A和点B的度规之00(元素).

考虑自由时空SF之观测者通过OA(c)观测太阳光谱的情形：M=MS，rA=RS，g00(rA)=1-2GM/(RSc2)；rB→∞，g00(rB)=1-2GM/(rBc2)→1.则式(9.27)可约化为

(9.28)

式中：G为万有引力常数；MS为太阳质量；RS为太阳半径；而ZE则是太阳光谱之爱因斯坦引力红移.

光子“静止质量”问题乃物理学重大问题之一.

式(9.28)是基于能移(energy shift)定义ZE=ΔK/K并由能量守恒原理导出的太阳光谱引力红移方程；而式(9.1)则是基于频移(frequency shift)定义ZE=Δf/f并由OA(η)时空变换因子γ=dt/dτ导出的太阳光谱引力红移方程.式(9.1)中，太阳光谱引力红移理论值为：ZE=-GMS/(RSc2)=-2.12×10-6.依据Adam[82]、Blamont和Roddier[83]，以及Brault[84]等的工作，这一理论值似已得到观测和实验验证.

如此，对照式(9.28)和式(9.1)，应成立：

即

(9.29)

式中：m为光子作为光学代理OA(c)之“信息子”时所呈现的观测质量；而f为光子作为光学代理OA(c)之“信息子”时所呈现的观测频率.

将式(9.29)之结论mo=m代入式(9.27)可得

(9.30)

这正是爱因斯坦光之引力红移方程(9.14).

式(9.30)，既印证了基于能移定义的光之引力红移方程(9.27)，也印证了基于“时频比不变性”的光之引力红移方程(9.14)，同时，印证了光子“静止质量”之重要结论：mo=m=hf/c2.

实际上，式(9.25)显示，引力红移之能移定义ZE=ΔK/K和频移定义ZE=Δf/f是等价的.因此，式(9.28)与式(9.1)本是等价的，或者，更严格地说，式(9.27)与式(9.14)是等价的，应成立：

即

(9.31)

式(9.29)和式(9.31)意味着：无论基于太阳光谱之引力红移的观测实验，还是基于光之引力红移之“能移”定义和“频移”定义的等价性，光子作为光学代理OA(c)之“信息子”所呈现的观测质量m即光子之“静止质量”mo；并且，光子之“静止质量”mo可由光子作为OA(c)之“信息子”所呈现的观测频率f计算——不同频率的光子具有不同的“静止质量”.

更精确的观测和实验留给实验物理学家们吧！

9.3.3 牛顿光之引力红移方程

至此，光子有了“经典质量”m∞和“静止质量”mo.如此，我们便可计算光子之经典动能和光子之经典势能，进而真正地基于牛顿万有引力论和经典力学，演绎牛顿光之引力红移方程.

根据OR和GOR理论，光之引力红移的本质并非引力时间“膨胀”.无论引力时间之“膨胀”或“势钟慢”效应，皆观测效应，乃观测代理OA(η)之观测局域性(η<∞)所致.根据第4章之“伽利略时空定理”，理想代理OA∞之下，η→∞，引力时间之“膨胀”和“势钟慢”效应随之消失.

光之引力红移的本质，是能量守恒和能量形式的变换，遵循物理学之能量守恒原理.因此，光之引力红移的定义和演算，应基于能量的观点或能量守恒的思想，而非引力场之“时间膨胀”效应.

光子频率f代表着光或光子的动能K：光学代理OA(c)之下，K=E=mc2=hf，式中m乃光子相对论性质量；而理想代理OA∞之下，K=m∞c2/2=moc2/2，式中，m∞为光子经典质量，mo为光子静止质量.根据OR理论，在不同观测代理之观测下，光之频谱不同；特别地，理想代理OA∞之下，光之频谱将会是不可观测的.如此，光学代理OA(c)之下，光之引力红移定义Δf和Z=Δf/f将不再适用于理想代理OA∞，或者说，不再适用于牛顿万有引力论和经典力学.

与一般物质粒子的情形一样，光子在引力场中运动，若势能V增加，则动能K衰减.本质上，光之引力红移是光子动能的衰减或“红移”.因此，无论理想代理OA∞还是光学代理OA(c)下的光之引力红移，皆可定义为光子动能的衰减或“红移”.

引力场中物质粒子动能K和势能V此消彼长.根据能量守恒原理：ΔK=-ΔV.

因此，基于能量的观点和能量守恒原理，因循式(9.25)的逻辑，牛顿的光之引力红移可定义为

(9.32)

式中：ZN为牛顿光之引力红移理论中的相对引力红移(ZN<0时意味着“红移”)；K和ΔK分别为理想代理OA∞之光子经典动能及其增量；V和ΔV分别为理想代理OA∞之光子经典势能及其增量.

特别需要指出：采用式(9.32)定义牛顿光之引力红移，图9中被观测的引力红移对象不再是静止于点A的光源(势钟)T，而是光子；观测代理为理想代理OA∞，因而，传递引力红移信息的“信息子”不是光子本身，而是OA∞速度无穷的理想化信息子.在经典力学中，光子失去了作为“信息子”的特殊地位，与一般物质粒子并无二致.

如此，光子在引力时空中的经典动能Kr和经典势能Vr应按式(9.24)计算：

(9.33)

式中：mo为光子“静止质量”；Kr和Vr分别为光子距离引力中心r时的经典动能和经典势能；KF=moc2/2为光子在真空或自由时空SF中的动能，且KF=Kr+Vr.

针对图9所描述的光之引力红移场景：ΔV=VB-VA，根据式(9.32)和式(9.33)，成立：

(9.34)

式中：光子“静止质量”mo即光子在理想代理OA∞观测之下的“经典质量”m∞；KB为光子距离引力中心rB时OA∞的经典动能；VA和VB分别为光子距离引力中心rA和rB时OA∞的经典势能.

此即真正的牛顿光之引力红移方程.

式(9.34)完全基于牛顿万有引力论和经典力学，与相对论和爱因斯坦公式E=mc2以及量子论和普朗克方程E=hf无关，不同于爱因斯坦光之引力红移方程(9.10)和伪牛顿光之引力红移方程(9.20).

考虑自由时空SF之观测者基于OA∞观测太阳光谱的情形：M=MS，rA=RS，rB→∞；式(9.34)约化为

(9.35)

式中：G为万有引力常数；MS为太阳质量；RS为太阳半径；而ZN则是太阳光谱之牛顿引力红移.

这与我们以往的认知不同，与伪牛顿引力红移方程(9.20)的结论不同：就太阳光谱而言，式(9.35)中的牛顿引力红移ZN并不等同于式(9.1)中的爱因斯坦引力红移ZE，而是ZE的2倍：ZN=2ZE.

稍后，牛顿光之引力红移方程(式(9.34)(9.35))的正确性，将会得到GOR引力红移理论以及GOR光之引力红移方程的印证.

9.4 GOR理论与光之引力红移

GOR理论也能预测光之引力红移.

GOR理论乃一般观测代理OA(η)之理论.可以预计，GOR理论对光之引力红移的预测，依赖于观测代理OA(η)，依赖于OA(η)之“信息波”速度η：不同观测代理之下，光或光子会有不同的引力红移.或者说，对于同一光之引力红移场景，不同的观测代理将会呈现出不同程度的光之引力红移.

无论爱因斯坦引力红移方程，还是牛顿引力红移方程，都只是GOR引力红移理论的部分理论.

9.4.1 一般观测体系之引力红移

类比爱因斯坦演绎光之引力红移方程(9.10)的逻辑路线，基于PGC对应原理，无论因循PGC逻辑路线1还是因循PGC逻辑路线2，GOR理论皆可导出与式(9.10)同构一致的GOR引力红移方程.

特别需要指出，原本，爱因斯坦引力红移理论意在探究引力场中光之频率的衰减或“红移”.而实际上，爱因斯坦引力红移方程(9.10)或式(9.14)是光学代理OA(c)之观测时间的“引力红移”方程，其逻辑演绎基于OA(c)观测时间的“引力膨胀”效应.如9.2.3所述：爱因斯坦广义相对论之引力红移理论是光学观测代理OA(c)的引力红移理论，代表着整个光学代理观测体系的引力红移.

因此，GOR理论，作为一般观测代理OA(η)之理论，若基于PGC原理导出与式(9.10)或式(9.14)同构一致的GOR引力红移方程，那将是OA(η)之“信息波”和“信息子”的引力红移方程，而非光之引力红移方程，除非，OA(η)即光学观测代理OA(c).

GOR理论将基于“时频比不变性”，并且，因循PGC原理，类比9.2.2之逻辑，演绎一般观测代理OA(η)之“信息波”或“信息子”的引力红移方程.

与光学观测代理OA(c)之情形类似，对于GOR理论之一般观测代理OA(η)，理论上，图9中的时钟T可以是任意波或任意周期性物质运动；然而，T从点A向点B辐射的信号并非光或光子，而是OA(η)之“信息波”或“信息子”，是OA(η)之观测媒介，携带着T之信息，包括其时间信息和空间信息.

对于一般观测代理OA(η)，其GOR时空变换因子Γ(η)=dtη/dτ(dτ乃“原时”或“固有时间”)，成立：

故

(9.36)

式中：η为OA(η)之“信息波”速度；tη=t(η)为OA(η)之观测时间，依赖于OA(η)及其“信息波”速度η.

根据OR和GOR理论，不同观测代理OA(η)，其“信息波”或“信息子”具有不同的频谱fη=f(η)，然而，同样遵循“时频比不变性”：

(9.37)

其中，特别注意，dtηA和dtηB皆可视为时钟T之观测时间，fηA和fηB皆可视为时钟T之观测频率.

一般观测代理OA(η)之“信息波”或“信息子”，其引力红移应定义为：ZOA(η)=Δfη/fη.针对图9之引力红移的场景，OA(η)之“信息波”或“信息子”的引力红移方程可基于“时频比不变性”导出

(9.38)

式(9.38)与光之引力红移方程(9.10)(9.14)同构一致.这里，再次强调，GOR引力红移方程(9.38)并非光之力红移方程，而是一般观测代理OA(η)之“信息波”的引力红移方程.ZOA(η)代表OA(η)整个观测体系的引力红移：ZOA(η)既是OA(η)之“信息波”和“信息子”的引力红移，也是OA(η)之观测时间的引力红移，乃至一切物质体系之广义德布罗意物质波的引力红移；并且，OA(η)可以是任意观测代理，而η可为任意物质运动速度.

式(9.38)表明，不同的观测体系或不同的观测代理OA(η)，其“信息波”速度η不同，因而，其观测时间dtη之“引力膨胀”不同，其观测频率fη之引力红移不同.特别地，考虑自由时空SF之观测者基于特定观测代理OA(η)观测OA(η)自身“信息波”之频谱的情形：rB→∞，g00(rB)→1；式(9.38)约化为

(9.39)

式(9.38)(9.39)可计算任意观测代理OA(η)之“信息波”之频谱的引力红移ZOA(η)(包括理想观测代理OA∞和光学观测代理OA(c)).

对于理想观测代理OA∞：η→∞，设图9之T从点A向点B发射OA∞之“信息波”和“信息子”，则

(9.40)

这意味着，理想化的OA∞，其“信息波”和“信息子”的观测频率无引力红移：ZOA(∞)=0；理想化的OA∞之观测时间无“引力膨胀”：dt/dτ=1.这与第4章中“伽利略时空定理”之结论是相同的.

对于光学观测代理OA(c)：η→c，设图9之T从点A(太阳表面：M=MS和rA=RS)向点B发射OA(c)之“信息波”(光)和“信息子”(光子)，则

(9.41)

其中，ZOA(c)正是爱因斯坦光之引力红移方程(9.1)或(9.11)中的太阳光谱之引力红移ZE.

可见，一般地，GOR引力红移方程(9.38)并非光子的引力红移方程，而是OA(η)之“信息子”的引力红移方程.仅当OA(η)为OA(c)时，式(9.38)约化为爱因斯坦光之引力红移方程(9.10)或式(9.14)，这时，ZOA(η)即光学代理OA(c) 观测下的光之引力红移ZE.

9.4.2 一般观测代理下的光之引力红移

如9.2和9.4.1所述，光之“引力红移”可以通过光学观测代理OA(c)进行观测：一种形式是，光作为OA(c)之“信息波”，光子作为OA(c)之“信息子”，其引力红移依光或光子频率的频移定义ZE=Δf/f，并依光之引力频移方程(9.10)或式(9.14)计算；而另一种形式则是，光子作为OA(c)之被观测对象，其引力红移依光或光子能移定义ZE=ΔK/K，并依光之引力能移方程(9.30)计算.

光之引力红移也可以通过其他的观测代理OA(η)进行观测，比如，9.3.3中牛顿光之引力红移方程(9.34)即理想代理OA∞观测光之引力红移的理论模型，其中，光子与一般被观测的物质粒子一样，是OA∞的被观测对象，而非OA∞之“信息子”.根据OR理论，观测代理OA(η)的速度η必须大于或等于被观测对象之运动速度v；因此，当光子作为OA(η)之被观测对象时，要求：η≥c.

借助观测代理OA(η)(η≥c)观测或测定光之引力红移，可因循和类比9.3.2、9.3.3中基于能移定义ZE=ΔK/K演绎方程(9.27)和方程(9.34)的逻辑路线，演绎推导观测代理OA(η)(η≥c)下的光之引力红移方程.

GOR光之引力红移的定义——

如9.3.2、9.3.3所述，光之引力红移的本质是能量守恒和能量形式的变换，遵循物理学之能量守恒原理.PGC对应原理之下，基于能量的观点和能量守恒的思想，因循式(9.25)和式(9.32)的逻辑，GOR理论将一般观测代理OA(η)观测下的光之引力红移定义为

(9.42)

式中：ZGOR乃OA(η)(η≥c)观测下的光之引力红移(ZGOR<0时意味着“红移”)；Kη和ΔKη分别为OA(η)观测下的光子相对论性动能及其增量；Vη和ΔVη分别为OA(η)观测下的光子相对论性势能及其增量.

一般观测代理观测下的光子能量——

考虑OA(η)(η≥c)观测下的球对称引力场，设光子动能为Kη，势能为Vη.基于PGC对应原理，因循爱因斯坦相对论的逻辑，类比光学代理OA(c)之式(9.26)中的情形，可计算观测代理OA(η)(η≥c)观测下的光子观测动能Kη和光子观测势能Vη：

(9.43)

式中：χ为牛顿引力势；mo为光子“静止质量”；mη为光子的OA(η)观测质量；Eη和KFη分别为光子在自由时空SF中的OA(η)观测总能量和观测动能；Kηr和Vηr分别为光子距离引力中心r时的OA(η)观测动能和OA(η)观测势能，KFη=Kηr+Vηr.

特别需要说明：在式(9.42)和式(9.43)中，被观测的对象是光子，其速度v即光子速度(弱场时，v≈c；特别地，χ=0时v=c)，而η则为观测代理OA(η)之“信息波”速度；Eη=mηη2即OR质能关系；Γ=Γ(η)为GOR理论之时空变换因子(参见第3章式(3.35))，其中，Γ|χ=0可谓“惯性时空变换因子”，Γ|v=0可谓“引力时空变换因子”：

(9.44)

这里，χ=0代表被观测对象不受引力作用时的状态，即在惯性时空中处于惯性运动(v)时的状态；而v=0则代表被观测对象处于静止状态，即在引力时空中处于引力作用(χ)时的状态.

惯性时空变换因子Γ|χ=0涉及OA(η)之相对论性动能KFη和Kηr的测定；而引力时空变换因子Γ|v=0则涉及OA(η)之相对论性势能Vηr的测定.

特别值得注意，OA(η)之观测动能和观测势能式(9.43)，既概括了爱因斯坦相对论(光学代理OA(c)情形)之相对论动能和相对论性势能公式(9.26)，同时，也概括了经典力学(理想代理OA∞情形)之经典动能和经典势能公式(9.33).

当观测代理OA(η)为光学代理OA(c)(η→c)时，式(9.43)中的光子动能KFη和势能Vηr约化为爱因斯坦之相对论性动能和相对论性势能：

(9.45)

式中：γ为爱因斯坦相对论之时空变换因子(式(3.12))；m为光学代理OA(c)观测下的光子相对论性质量，依爱因斯坦公式，OA(c)观测下的光子动能即E=mc2.

当观测代理OA(η)为理想代理OA∞(η→∞)时，式(9.43)中的光子动能KFη和光子势能Vηr约化为牛顿之经典动能和经典势能：

(9.46)

式(9.45)和式(9.46)印证了GOR能量公式(9.43)之逻辑上的自洽性，同时，印证了GOR能量公式(9.43)与爱因斯坦相对论之能量公式和牛顿力学之能量公式逻辑上的一致性.

GOR光之引力红移方程的演绎——

针对图9所描述的光之引力红移场景：ΔV=VB-VA，根据式(9.42)和式(9.43)，成立：

(9.47)

式中：mo为光子静止质量；mη为光子的OA(η)观测质量；KFη为光子在自由时空SF中的OA(η)观测动能；KB为光子距离引力中心rB时OA(η)的观测动能；VA和VB分别为光子距离引力中心rA和rB时OA(η)的观测势能；g00(rA)和g00(rB)分别为OA(η)之引力时空点A和点B的度规gμν之00(元素).

此即GOR理论的光之引力红移方程.

式(9.47)表明：光之引力红移ZGOR=ZGOR(η)(η≥c)依赖于观测代理OA(η)——不同观测代理，呈现出不同程度的光之引力红移：OA(η)之“信息波”速度η越大，其光之相对引力红移量ZGOR(η)就越大.

就太阳光谱之引力红移而言(rA=RS而rB=∞)：

η→c时，KFη=mc2，ZGOR(η)=-GMS/(RSc2)=ZE；

η→∞时，KFη=mc2/2，ZGOR(η)=-2GMS/(RSc2)=ZN.

如此，鉴于式(9.47)中的ZGOR(η)关于η∈[c,∞)的连续性和单调性，GOR光之引力红移ZGOR(η)满足

9.4.3 光之引力红移理论的统一

光之引力红移的预言是爱因斯坦基于“等效原理”做出的，而爱因斯坦光之引力红移方程则是基于广义相对论导出的.我们将基于爱因斯坦广义相对论的引力红移理论称为爱因斯坦引力红移理论.

人们试图基于牛顿万有引力论和经典力学建立牛顿引力红移理论，导出牛顿光之引力红移方程，以此对照并检验爱因斯坦引力红移理论和牛顿引力红移理论，进而，对照并检验爱因斯坦广义相对论和牛顿万有引力论.结果导出了“伪牛顿光之引力红移方程”.如式(9.21)所示，“伪牛顿光之引力红移方程”(式(9.20))，与爱因斯坦光之引力红移方程(式(9.10))近似，其太阳光谱引力红移理论值ZPN与爱因斯坦引力红移理论值ZE不具有观测上的可分辨性.

实际上，正如我们反复强调的，爱因斯坦广义相对论与牛顿万有引力论归属不同的观测代理，服务于不同的观测体系；二者不具有孰是孰非之可比性.不同观测代理之理论模型，包括光之引力红移理论，存在理论上的差异以及观测和实验上的不同是自然的或必然的；反之，却可能是不正常的，如“伪牛顿光之引力红移方程”之情形.

GOR理论完全基于牛顿万有引力论和经典力学导出了真正的牛顿光之引力红移方程(式(9.34))，其太阳光谱引力红移理论值ZN(式(9.35))是爱因斯坦太阳光谱引力红移理论值ZE(式(9.1))的2倍：ZN=2ZE.我们将真正基于牛顿万有引力论和经典力学的引力红移理论称为牛顿引力红移理论.

进而，GOR理论导出了一般观测代理OA(η)(η≥c)的光之引力红移方程(式(9.47))，即所谓“GOR光之引力红移方程”.我们将基于GOR理论的引力红移理论称为GOR引力红移理论.

GOR引力红移理论展现出GOR理论所具有的高度的一般性和概括性.

依9.3.2和式(9.29)(9.31)，光子在光学代理OA(c)观测下的观测质量m即光子静止质量mo.因此

(9.49)

于是，光学代理OA(c)之下(η→c)，成立：

(9.50)

这正是爱因斯坦光之引力红移方程(9.10)(9.14).

可见，当观测代理OA(η)为光学代理OA(c)时，GOR光之引力红移方程(9.47)便约化为基于爱因斯坦广义相对论的光之引力红移方程(9.10)(9.14).

理想代理OA∞之下，光子动量乃经典动量，即

(9.51)

于是，η→∞时，成立：

(9.52)

这正是牛顿光之引力红移方程(9.34).

可见，观测代理OA(η)为理想代理OA∞时，GOR光之引力红移方程(9.47)则约化为真正基于牛顿万有引力论和经典力学的牛顿引力红移方程(9.34).

GOR引力红移理论概括统一了爱因斯坦引力红移理论和牛顿引力红移理论，表明：GOR光之引力红移方程，逻辑上，既与爱因斯坦光之引力红移方程一致，又与牛顿光之引力红移方程一致；印证了GOR光之引力红移方程逻辑上的自洽性和理论上的正确性，同时，印证了纯粹基于经典力学的牛顿光之引力红移方程(9.34)的正确性.

10 GOR理论与引力波

或许，与爱因斯坦之三大预测——光之引力红移和光之引力偏折，以及水星反常进动——相比， “引力波”(gravitational wave)才是爱因斯坦广义相对论最具诱惑力的似是而非的预言.

GOR理论并不怀疑引力波和引力子的存在.

实际上，从某种意义上说，如同电磁场意味着“电磁波”，引力场则意味着“引力波”；如同电磁力或电磁相互作用需要“光子”作为媒介子，引力或引力相互作用则需要“引力子”作为媒介子.

然而，这并不意味着爱因斯坦正确地预测了引力波，也不意味着LIGO[101-102]真地探测到引力波.

实际上，无论牛顿万有引力论或爱因斯坦广义相对论，其公理体系或逻辑前提中，皆不存在任何有关引力辐射速度的先验知识或先验信息.正如第3章之“3.1.1 引力局域性”所述，无论牛顿万有引力论还是爱因斯坦广义相对论，其中，都隐喻着一个重要的理想化假设：引力乃超距作用，辐射速度无穷.

牛顿意识到这种理想化假设是非客观和非现实的[103]：“就哲学意义而言，无穷的引力速度是荒谬的！”爱因斯坦也不认为物理世界存在超距作用.然而，因为没有关于引力辐射速度的先验知识——直到今天也没有，所以牛顿万有引力定律未计引力相互作用之局域性.同样地，爱因斯坦广义相对论也未考虑引力相互作用之局域性.根据广义相对论，弱引力场之情形下，爱因斯坦引力场方程约化为牛顿万有引力定律之泊松方程形式.我们不能设想，引力辐射速度依赖于引力场之强弱——强则慢；弱则快，甚至无穷.

实际上，正如第3章之“3.1 引力时空之局域性问题”所述，爱因斯坦广义相对论中的局域性，只是观测上的局域性，而非引力相互作用之局域性.

那么，爱因斯坦是如何预言其“引力波”的呢？

爱因斯坦之“引力波”预言存在2个问题：

第二，引力波辐射速度真地是光速c吗？

GOR理论将为我们解析爱因斯坦之“引力波”预言：解析爱因斯坦之“引力波”方程的真伪，解析LIGO之“引力波”探测的真伪！

10.1 爱因斯坦之波方程：引力波预言

“引力波”的概念，据说，最早由爱因斯坦和爱丁顿提出.而正式的“引力波”预言则应该是爱因斯坦基于其广义相对论导出的“引力波”方程[104-105].

关于“引力波”，爱因斯坦一如既往地将“弱场近似”法作为其广义相对论的一种线性化理论，借助“弱场近似”法将非线性的引力时空问题简化为线性的引力场问题.基于“弱场近似”逻辑和“弱场近似”法，引力时空之度规gμν(xα,c)近似闵科夫斯基度规ημν时，非线性的爱因斯坦场方程近似于线性方程；如此，爱因斯坦便可演绎其“引力波”方程.

如第4章之4.1.2所述：观察爱因斯坦广义相对论之时空变换因子γ(式(3.16))可知，欲令引力时空之度规gμν(xα,c)≈ημν，需要营造“弱引力场”之情景：|χ| ≪c2和|γivi|≪c.如此，引力时空之度规gμν(xα,c)则可线性化作式(4.1)：

|χ|≪c2， |γivi|≪c:
gμν(xα,c)=ημν+hμν(xα,c)(|hμν|≪|ημν|)

此即“弱场近似”法之“弱场”条件.式中：ημν=diag(+1,-1,-1,-1)可称作“平度规”；而hμν则可称作“曲度规”(hμν及其各阶导数皆小量).

特别注意，“弱场”条件中的“曲度规”hμν被爱因斯坦视为“平直”时空背景(ημν)下的“弱引力势”，是微弱引力辐射对“平直”时空的搅扰，致使原本“平直”的时空泛起细微的“涟漪”.

实际上，如第4章之“4.1.3 弱场近似条件”所述，归纳起来，“弱场近似”法所涉及的假设条件不仅仅要求：第一，弱场；还要求：第二，低速，第三，静态，第四，时空正交，第五，调和坐标.

回顾爱因斯坦基于其“弱场近似”法演绎其“引力波”方程的思想方法和逻辑过程，有助于我们理解和认识爱因斯坦之“引力波”预言及其“引力波”方程，为我们稍后演绎GOR“信息波”方程提供可因循的逻辑路线，并将爱因斯坦“引力波”方程作为GOR“信息波”方程的类比对象.

介绍爱因斯坦广义相对论的书籍或文献大多有关于爱因斯坦“引力波”方程及其演绎的内容.以下有关爱因斯坦“引力波”方程的描述较为符合爱因斯坦“引力波”方程的原貌，主要参阅文献[60，106]，以及文献[107].

爱因斯坦场方程(式(5.2))之左端通常被定义或标记为张量Gμν(c)，即所谓“爱因斯坦张量”，而爱因斯坦场方程则可简洁地写作

(10.1)

式中：Rμν为里奇张量(代表时空曲率)；R为高斯曲率；gμν为时空度规；Tμν为能动张量；而κ则为爱因斯坦场方程之系数.

因循爱因斯坦“弱场近似”法之逻辑，在第4章之4.1.3所列“弱场近似”条件之下，里奇张量Rμν和高斯曲率R分别近似为

(10.2)

定义“度规摄动”(metric perturbation)张量：

(10.4)

并且，相应的场方程之坐标条件约化为

(10.5)

满足坐标条件(10.5)的场方程(10.4)有如下解：

(10.6)

式中：积分域为引力源所占据的3d空间；xi(i=1,2,3)为观测者坐标这；x′i(i=1,2,3)为物质分布坐标；|xi-x′i|即观测坐标xi和引力物质坐标x′i之间的距离.

这里，所谓“推迟”，具有重要的寓意，乃“局域性原理”(principle of locality)的体现：根据局域性原理，能量或信息跨越空间需要时间.因此，对于被作用物体，力或能量乃“推迟”的物质相互作用；对于观测者，信息乃“推迟”的物理信号.

至此，引力辐射的速度似乎可以得到确认，然而，关于引力之“波”的概念尚未形成.

或

(10.7)

由此，便诞生了“引力波”的概念和预言.

之后，类比“电磁波”的量子化，“引力波”被量子化；类比作为电磁相互作用媒介子的“光子”，人们构建了“引力子”的概念，设想“引力子”即引力相互作用之媒介子.根据爱因斯坦狭义相对论之质速关系，任意以真空光速c运动的物质粒子，其“静止质量”皆应为零.如此，“引力子”被设置为“静止质量”为零且“自旋”为2的基本粒子.

然而，爱因斯坦关于“引力波”和“引力子”之理论上的预测，似乎从一开始就是错误的.

10.2 引力波探测：LIGO工程

本着物理学之实证原则，理论上做出“引力波”预言之后，剩下的便是探测“引力波”，证实“引力波”的存在.于是，物理学一场耗时耗钱耗力的“引力波”探测活动便开始了.

“引力波”被视为爱因斯坦广义相对论实证中最后一块缺失的拼图.2015年，LIGO宣布首次探测到“引力波”；2017年，LIGO团队主要成员Weiss，以及Barish和Thorne，因探测到“引力波”而获得当年度诺贝尔物理学奖.至此，LIGO大功告成，爱因斯坦广义相对论神圣不可侵犯的地位得以进一步巩固.

回顾“引力波”的探测历史，解析LIGO之“引力波”探测工程，有助于我们对“引力波”探测原理和探测方案设计，以及LIGO之探测过程和探测结论的认识，揭示爱因斯坦之“引力波”预测和LIGO之“引力波”发现的似是而非.

10.2.1 早期的原理性探测方案设计

探测“引力波”原本极其简单和平常：人们每天都在做着探测和利用“引力波”的事情.

然而，探测“引力波”似乎又极富挑战性.

相对于地球之观测者，地球引力场过于平静，缺少“波澜”，难以探测；并且作用于苹果的地球之引力辐射或引力波，看不见摸不着.或许，高速运动的致密星球或黑洞(那时黑洞的概念还未形成)能产生足够强劲的引力辐射或引力波，并且对地球平静的引力场构成搅扰或摄动.如此，我们便可设法探测由外太空传来的引力辐射或引力波.

如图10(a)所示，设想天平一端的托盘上放置一苹果，另一端的托盘上放置等质量的砝码；在近似稳态或静态的地球引力场中，天平左右两臂保持水平或平衡状态.为了增加分辨率和灵敏度，假设天平两臂足够长，砝码与苹果相距足够远.当外太空传来的引力辐射或引力波自上而下地掠过苹果时，苹果重量必定会有细微的变化，天平会失去平衡，或者，在平衡点附近呈现出摄动或震动状态.如此，我们便能观测到“波动”的引力辐射——“引力波”.

图10 引力波探测方案Fig.10 Detection scheme of gravitational waves

利用天平“称”引力波是一个好的想法：俄国科学家罗蒙若索夫曾用天平“称”得物质不灭定律.然而，实验物理学家会认为用天平“称”引力波很愚蠢：物质间的引力相互作用太弱，只有电磁力的1/1036；虽然外太空可能有强引力辐射源，却距离地球遥远，依照平方反比律，其对地球之天平上的单个探测物质(苹果)摄动极小.因此，利用天平很难称得“引力波”或“引力子”重量.

引力波问题以及引力波的探测问题，其复杂性还在于爱因斯坦之“引力波”预言本身的似是而非.自1916年爱因斯坦广义相对论建立，以及稍后“引力波”预言诞生，30～40年的时间里，物理学家甚至没能提出具体的引力波探测方案.直到1955年，英国物理学家Pirani[108]提出，引力辐射或引力波的探测应该基于黎曼张量分析；虽然利用单个测试物体(如图10(a)中天平上的苹果)测试引力波难以奏效，而如图10(b)所示，通过测试2个小质量物体(自身引力可忽略不计)之间距离的变化，可能探测到引力辐射或引力波.基于爱因斯坦广义相对论，Pirani证明：引力辐射或引力波从2个物体之间穿过时，2个物体之间的距离会发生变化；穿越方式不同，或收缩或膨胀.

特别值得指出，直到今天，Pirani的引力波探测方案，仍然是引力辐射或引力波探测系统的原理性方案，并且，被LIGO之引力波探测系统借用.

受Pirani引力波探测思想和探测方案的启发，美国马里兰大学的Weber[109]开展了实际的引力辐射和引力波探测.Weber设计制作了探测引力波的引力波天线，后被称作“Weber棒”，一种铝制实心圆柱，长1～2 m，直径0.2～1.0 m.基于Pirani的理论，Weber认为，如图10(c)所示，当引力辐射或引力波扰动引力波天线时，Weber棒便会沿长度方向收缩或拉伸；当引力波频率与Weber棒共振频率一致时，这种收缩或拉伸的效应可以被Weber棒周围的压电传感器检测到并转换成为电信号，经电子放大器放大之后即可在示波器上呈现出引力波图像.

特别需要指出，Weber的引力波探测思想与Pirani是有区别的.依据爱因斯坦广义相对论[15]，引力时空会收缩或膨胀：空间可能伸缩；时间也可能伸缩，而时间的伸缩则可能意味着，引力场中物质(包括光或光子)之运动速度的变化.Pirani[108]认为，引力辐射或引力波会导致空间的伸缩；而Weber[109]则认为，引力辐射或引力波会导致物体的伸缩.当然，你可以认为，空间伸缩与物质伸缩是等效的：空间伸缩挤压或拉伸物体，导致其伸缩.Weber正是这样想的.

1968年，Weber[110-111]宣布，其Weber棒检测到引力波.然而，之后众多模仿Weber的重复性实验都未能利用Weber谐振棒探测到Weber所说的引力波.最终的结论是：Weber谐振棒之灵敏度不足以探测到Weber声称其探测到的引力辐射或引力波.

Weber探测系统的致命缺点是Weber棒太短，且难以加长，收缩和拉伸的效应极为有限，同时，制约于压电传感器的灵敏度，信号难以放大.

10.2.2 脉冲双星和引力波

射电天文学(radio astronomy)的发展开阔了人类的眼界，将人类借助电磁相互作用感知客观世界的频谱范围由可见光波段扩展到几乎整个电磁波段.20世纪天文学四大发现，类星体、脉冲星、星际分子和微波背景辐射，正是射电天文学的成果.然而，与光学天文学能直观地用眼睛看不同，射电天文学一半是听，一半是猜，似是而非，令人半信半疑.

“小绿人”和脉冲星——

探测引力波，需要有大质量致密星体作为引力波辐射源.天遂人愿——1967年，英国剑桥大学卡文迪许实验室博士研究生Bell，利用射电望远镜，发现狐狸星座有一颗星会发射周期性电磁脉冲信号，每间隔1.33 s便会出现一次[112].Bell及其导师Hewish经过计算和分析确认，这是一种未知天体，并且，将其命名为“脉冲星”(pulsar)[113].如此，Bell和Hewish便“发现”了第一例脉冲星：PSR1919+21.为此，1974年，Bell的导师Hewish成为第一个获得诺贝尔物理学奖的天文学家[114].

脉冲星被认为是一种高速旋转的中子星，其物质密度仅次于黑洞，可作为理想的“引力波”源.

值得思考的是，“脉冲星”是否真实地存在.

无论光学望远镜或射电望远镜，都不可能直观地辨认什么星体是中子星，更不可能看到它们在高速旋转.射电望远镜接收到的周期性电磁脉冲信号究竟意味着什么，天文学家只能猜；并且，这种猜想难以实证，似乎只能停留于猜想，只能通过观测或实验数据与猜想之数学模型的匹配，间接考证.浩瀚宇宙，什么样的可能都有.一开始，天文学家甚至以为，那些电磁脉冲是外星人向地球人发送的信号，因而，称PSR1919+21为“小绿人”.

Bell之前，中子星只是一个假设，以数学模型的形式存在于理论或计算机数据库中.Bell探测到星体周期性电磁脉冲信号之后，模拟计算显示，星体周期性电磁脉冲信号的宿主符合中子星那样体积小、密度高、质量大，并且高速旋转的星体.于是，脉冲星，既成为中子星之假设的产物，同时，反过来又成为中子星之假设的证据.“脉冲星”之假设和“中子星”之假设如此循环论证，逻辑上，似乎很有些可疑.

无论如何，脉冲星，或高速旋转的中子星，是解释星体辐射周期性电磁脉冲信号的一个选项.

据说，世界各天文台已累计发现脉冲星2 000余颗.2016年，中国建成口径500 m的“天眼”FAST射电望远镜.截至2021年12月20日，FAST已经发现脉冲星509颗，或许，更准确地说，已经接收到来自509颗星体的周期性电磁脉冲信号.

从脉冲星到脉冲双星——

“脉冲双星”(binary pulsar)乃双星系统：一颗脉冲星与一颗伴星相互环绕.脉冲星的伴星通常为白矮星或中子星；伴星也可以是脉冲星，这样的脉冲双星系统被称为“双脉冲星”(duble pulsar).

1974年，也就是Bell的导师Hewish获得诺贝尔奖的那年，美国马萨诸塞大学博士研究生Hulse受其导师Taylor指派去波多黎各Arecibo天文台参与脉冲星探测工作，那里有当时世界上口径最大(305 m)的射电望远镜.一天，Hulse探测到一个微弱的周期性电磁脉冲信号，可以确定，一颗新的脉冲星被发现.

然而，与一般脉冲星不同，这一脉冲星的脉冲周期本身是周期性变化的.Hulse猜想，这或许因为脉冲星正围绕着某个伴星运动而产生了多普勒效应.Hulse将其发现和猜测报告了导师Taylor.于是，Taylor飞抵Arecibo，与Hulse一起构建了脉冲双星系统的数学模型，计算得出：脉冲星绕伴星运动的轨道周期为7.75 h，脉冲星最大速度约300 km/s，伴星平均速度约200 km/s，而脉冲星和伴星平均距离大约相当于太阳半径[115].如此，Hulse和Taylor便“发现”了第一例“脉冲双星”[116]：PSR1913+16.

当初，Bell和Hewish猜测，射电望远镜接收到的周期性脉冲信号源于星体的自转；现在，Hulse和Taylor猜想脉冲星之周期的周期性变化源于星体的公转.其逻辑似有异曲同工之妙.

之后，很快便有人依据爱因斯坦广义相对论主张：理论上，脉冲双星会因引力辐射而损失其能量，导致PSR1913+16轨道旋进，其近伴星点有进动，半长轴和脉冲周期会逐渐缩短[117-119].为此，Taylor教授持续观测PSR1913+16数十年[120]；据说，观测值与理论值精确相符，相差仅为0.4%.这似乎意味着，Hulse和Taylor，不仅发现了“脉冲双星”，同时，还间接地证明了引力波的存在[121-122].一切似乎都朝着支持爱因斯坦广义相对论及其“引力波”预言的方向发展.

1993年，Hulse和Taylor获得诺贝尔物理学奖.

据说，世界各天文台已累计发现“脉冲双星”天体系统150余例；PSR1913+16是第一例，并且，被持续观测了数十年[120].有人认为，PSR1913+16“提供了对爱因斯坦广义相对论迄今最精确的检验”.

值得思考的是，“脉冲双星”是否真实地存在.

如同“中子星”和“脉冲星”本质上是一种猜想一样，“脉冲双星”本质上也是一种猜想.无论光学望远镜或射电望远镜，都不可能直观地辨认脉冲双星系统.PSR1913+16之脉冲周期为什么会周期性地变化，Hulse和Taylor也只能猜.无论PSR1913+16之观测数据与数学模型匹配有多么好，都不能证明“脉冲双星”真实地存在.实际上，基于GOR理论，正是PSR1913 +16观测数据与数学模型的“精确匹配”，暴露出PSR1913+16作为“脉冲双星”，其轨道旋进以及周期和半长轴的变化存在诸多疑点.

无论如何，脉冲双星是解释PSR1913+16电磁脉冲信号周期之周期性变化的一个选项.

10.2.3 LIGO探测器及其探测原理

LIGO的使命即探测爱因斯坦预言的“引力波”.

LIGO原型出自美国麻省理工学院Wesis教授.20世纪70年代，Wesis发展了探测引力波的激光干涉术.实际上，LIGO探测器类似迈克尔逊干涉仪(Michelson interferometer)，即迈克尔逊和莫雷1887年用于探测“以太”(ether)的光干涉系统[42].迈克尔逊- 莫雷实验虽未探测到“以太”，却导致了“光速不变性原理”的建立，并且，最终导致爱因斯坦狭义相对论乃至爱因斯坦广义相对论的建立.

LIGO探测系统之基本结构如图11(a)所示，其探测引力波的基本原理源于Pirani[108]的思想和理论.Pirani基于爱因斯坦广义相对论认为：引力辐射或引力波会导致空间收缩或拉伸；测试2个物体空间距离的变化，即可探测掠过测试物体的引力波.

实际上，Weber的引力波探测系统，其基本原理也是基于Pirani之思想和理论的.然而，Weber棒太短，其伸缩的物理效应极其有限，难以感应或探测到掠过Weber棒的引力辐射或引力波.

LIGO探测器在系统结构上，如图11(a)所示，是对迈克尔逊干涉仪的模仿：核心是相互垂直的2个激光臂(X和Y)，各激光臂安装有2个相距L=4 000 m的测试质量体(L即激光臂长度)；激光沿激光臂在2个测试质量体之间的F-P真空谐振腔(Fabry-Pérot cavity)中多次往返，其等效臂长可达1.12×106m，是Weber棒的5×105倍.

可见，LIGO系统探测引力辐射和引力波的灵敏度是Weber探测系统所不可比拟的.

LIGO探测器在工作进程上，如图11(a)所示，也是对迈克尔逊干涉仪的模仿：激光器LS发射一束频率稳定的单色激光，经分束器BS分为强度相同的2束激光，一束进入X-光臂，另一束进入Y-光臂，在激光臂之F-P真空腔中旅行1.12×106m之后，2束激光返回分束器BS汇合，产生干涉，或相长，或相消；干涉效应由光探测器PD记录.依爱因斯坦广义相对论，引力辐射或引力波掠过LIGO探测器时，X和Y两个激光臂，一个拉伸，而另一个则会收缩，导致2束激光出现光程差，产生干涉条纹.如此，LIGO探测器便可记录下引力辐射或引力波的相关信息.

图11 LIGO探测器之体系结构和原理Fig.11 Architecture and principles of LIGO’s detection system

1991年，美国麻省理工学院和加州理工学院，在美国国家科学基金委的支持下，正式开始联合建设LIGO探测系统.为了提高探测引力波的可靠性，LIGO共建设2个探测基站：一个位于美国路易斯安那州的Livingston，另一个位于美国华盛顿州的Hanford，相距约3 002 km(相当于约10 ms的光程).实际上，如图11(b)所示，LIGO建设2个引力波探测基站的真正用意还在于，基于“三边测量法”对引力波源进行定位，并且，测定引力波的速度.

LIGO于1999年底建设完成.或许因为建成之后的LIGO一致未能探测到引力波，2005—2007年，LIGO进行了升级改造.升级改造后的LIGO谓之Advanced LIGO，或称aLIGO.

LIGO逐渐发展成国际性引力波探测科学联合体：LIGO科学合作组织(LIGO Scientific Collaboration, LSC).欲对引力波源准确定位，地球表面至少需要构建3个引力波探测基站.2007年，欧洲引力波天文台组建的Virgo基站与LIGO的2个基站开始并网运行.同时，全世界所有的天文台，包括光学的和射电的，都参与到了LIGO探测引力波的活动中，对引力波开展所谓全方位多信使的探测.

10.2.4 LIGO的探测目标

探测引力波，自然需要引力波源作为探测目标.

我们无须证明引力辐射或引力波的存在.大海是天然的引力波天文台.大海作为引力波探测器，其探测目标，即可探测的引力源或引力波源，既包括月亮也包括太阳.大海的潮汐早已经告诉我们，星体会辐射引力或引力波.

任何物质体，包括太阳、地球、月亮、苹果，甚至光子，都是引力辐射之源或引力波之源.

苹果质量小，比不得星体.然而，苹果可以充分接近LIGO探测器.理论上，依平方反比律，苹果充分地接近LIGO探测器时，其引力辐射强度或引力波强度将被充分地放大；如此，LIGO探测器或许能探测到苹果辐射的引力波.相对于LIGO探测器，苹果的体积和质量或许太小，可以换作火车.假设一列火车紧贴着LIGO一激光臂行驶；或许，火车远大于苹果的质量能搅扰LIGO周围时空，令其泛起足够的“涟漪”.如此，LIGO是否应该能够探测到火车的引力辐射或火车辐射的引力波呢？

总之，地球表面有足够多的引力波源供LIGO探测.然而，LIGO却舍近求远，试图探测到来自其他星球的引力辐射或引力波.那么，什么样的星体适合作为LIGO探测器的探测目标或引力波源呢？

自然地，对是否可作为探测目标或引力波源的候选星体，LIGO一定进行过大量而细致的测算.

让我们随LIGO一起一一甄别之.

首先是地球.任意物质体系皆因物质分布而形成引力场，同时，辐射引力或引力波.自然地，地球也不例外；地表之一切物体皆受地球引力作用.LIGO探测器位于地球表面，处于地球之引力场中，那么，地球之引力辐射或地球之引力波为什么不会触发LIGO探测器呢？地球引力场近似球对称引力场，于地表(球面)处处均匀对称且等势.LIGO探测器与地球相对静止；就LIGO周围时空而言，地球之引力场乃稳态或静态引力场.因此，无外来之引力辐射或引力波侵入时，LIGO探测器之X-光臂和Y-光臂中的2束激光无光程差，激光干涉器不会形成干涉.如此，地球之引力辐射或地球之引力波不会触发LIGO探测器.

其次是月亮，距离地球最近的星体.月亮的质量远大于苹果和火车，其引力辐射或引力波能被地球大海感应，形成潮汐.然而，LIGO并未探测到月亮之引力辐射或月亮之引力波.实际上，月亮引力场也近似于球对称引力场，于地球表面近似处处均匀对称且等势.相对于地球表面，月亮之引力场移动缓慢；就LIGO周围时空而言，月亮之引力场同样近似稳态或静态引力场，因此，难以触发LIGO探测器.

再者是太阳，距离地球最近的恒星.太阳的质量远远大于月亮，能够辐射出强度远远超过月亮的引力或引力波，其引力辐射也能被地球大海感应，形成潮汐.然而，太阳与地球的距离远大于月亮与地球的距离；对于地球之大海，太阳的引潮力只相当于月亮引潮力的1/2.并且，与月亮之引力场的情形一样，就LIGO周围时空而言，太阳之引力场也近似于稳态或静态引力场，因此，同样难以触发LIGO探测器.

剩下的候选只能是太空深处的星体，距离地球遥远，必须具有更大的质量.

或许，“脉冲星”可作为LIGO的探测目标或引力波源之候选星体.脉冲星乃中子星，密度高、质量大，并且，高速旋转，理论上，应能辐射出高能量的引力或引力波.然而，脉冲星似乎未能通过LIGO的候选测试.那么，“脉冲双星”呢？与单个脉冲星相比，脉冲双星系统除星体密度高、质量大且高速自旋外，还多了一颗致密的伴星，并且，双星近距离高速环绕，理论上，应该能辐射出更高能量的引力或引力波.然而，脉冲双星似乎也未能通过LIGO的候选测试.

其实，无论脉冲星还是双脉冲星，即使黑洞甚至双黑洞，也难以通过LIGO的候选测试.除距离和质量因素外，类似于月亮和太阳之引力场，相对于地球或LIGO探测器，无论中子星还是黑洞，无论双中子星还是双黑洞，其引力场，或其辐射的引力或引力波，皆近似于稳态或静态引力场，因而，同样难以触发LIGO探测器；除非，能像一些天文学家所设想的[117-119]，双星并合(coalescence)，剧烈爆发.

Weisberg和Taylor[120]对Hulse-Taylor脉冲双星的持续观测及其模拟计算显示，PSR1913+16绕伴星环绕的椭圆轨道之周期每年减少76.5 μs，半长轴每年缩短3.5 m，预示着Hulse-Taylor脉冲双星终将并合.LIGO基于爱因斯坦广义相对论建立双星系统动力学模型，并且，借助超距计算机对双星系统的演化进行模拟[123-126].这涉及一项新的计算机应用技术：数值相对论(numerial relativity).所谓“数值相对论”，即基于爱因斯坦的理论，包括狭义相对论和广义相对论，用数值模拟的方法，在计算机上演绎动力学系统的运动过程，例如，双星天体的演化及至并合.LIGO基于数值相对论的计算机模拟结果显示：双星系统，特别是双黑洞天体，当其并合时，可能瞬间喷发出足以触发LIGO探测器的高能引力辐射或高能引力波.

于是，LIGO团队将LIGO探测器之探测目标指向了双星系统，特别是双黑洞天体，并且，期待着它们的并合和剧烈喷发.

然而，关于双星系统特别是双黑洞系统是否真实存在的疑虑并未消除.双星并合时的引力时空不再是稳态时空或静态时空.然而，特别值得注意：双星并合辐射的引力或引力波近似球面波，其场强随距离依平方反比律衰减，并且，球面近似均匀对称等势，难以令LIGO之激光干涉仪产生干涉效应.

10.3 GOR理论之波方程：信息波方程

第3章3.1.1之“引力局域性”指出，爱因斯坦广义相对论和牛顿万有引力论同样隐喻着一个重要的理想化假设：引力乃超距作用，辐射速度无穷；其公理体系或逻辑前提中不存在任何有关引力辐射速度的先验知识或先验信息.

因此，逻辑上，爱因斯坦广义相对论不可能得出引力辐射速度或引力波速度即光速的结论.

10.3.1 GOR波方程的演绎

基于PGC对应原理，GOR波方程的演绎类比爱因斯坦广义相对论的逻辑，却并未沿袭爱因斯坦的“弱场近似”逻辑或“弱场近似”法.如同第5章中GOR场方程的建立和第6章中球对称引力时空之GOR场方程的解，GOR波方程的演绎采用GOR理论之“理想逼近”逻辑和“理想代理”法.

此即GOR“理想代理”法之“时空平直”条件，其中：曲度规hμν及其各阶导数皆小量；根据“伽利略时空定理”，η→∞时，gμν(xα,η)→ημν，即hμν→0.

GOR“理想代理”法之“理想逼近”条件仅要求：观测代理OA(η)之信息波速度η足够大或η→∞.

爱因斯坦通过“弱场近似”法令光学观测代理OA(c)之引力时空X4d(c)近似平直，进而将爱因斯坦场方程线性化；而GOR理论则通过“理想代理”法令一般观测代理OA(η)之引力时空X4d(η)趋于平直，进而将GOR场方程线性化.然而，这并不意味着OA(η)之引力场必须为“弱场”.如此，GOR理论之“时空平直”条件中的“曲度规”hμν，不再是“平直”时空背景(ημν)下的弱引力势或弱引力辐射对“平直”时空ημν的搅扰；“引力波”也不再是“平直”时空因弱引力辐射的搅扰而泛起的细微“涟漪”.

如同爱因斯坦场方程(式(5.2))，GOR场方程(式(5.32))之左端可以类似地定义或标记为GOR张量Gμν(η)，而GOR场方程则可简洁地写作

(10.9)

式中：η代表一般观测代理OA(η)之“信息波”速度；Rμν=Rμν(η)为OA(η)之里奇张量(代表OA(η)之时空曲率)；R=R(η)为OA(η)之高斯曲率；gμν=gμν(η)为OA(η)之时空度规；Tμν=Tμν(η)为OA(η)之能动张量；而κη=κη(η)则为OA(η)之GOR场方程系数.

“理想逼近”条件：η足够大或η→∞时，依第5章之5.6及其式(5.59)，里奇张量Rμν(η)和高斯曲率R(η)分别近似或趋于

(10.10)

定义OA(η)之度规摄动张量：

(10.11)

并且，相应的场方程之坐标条件约化为

(10.13)

(10.14)

式中：积分域为引力源所占据的3d空间；xi(i=1,2,3)为观测者之坐标；x′i(i=1,2,3)为被观测对象之坐标；而|xi-x′i|则是观测者的坐标xi与被观测对象的坐标x′i之间的距离.

然而，特别需要指出，这里的“推迟”依赖于观测代理OA(η)之“信息波”速度η，而非光速c；或者，更明确地，这里的“推迟”并非引力或引力辐射的“推迟”，而是观测信息的“推迟”，乃观测代理OA(η)之观测局域性(η<∞)所致.

或

(10.15)

注意，GOR波方程(10.15)概括了爱因斯坦波方程(10.7)：观测代理OA(η)为光学代理OA(c)时，GOR波方程(10.15)即爱因斯坦波方程(10.7).

至此，或许终于领悟：爱因斯坦广义相对论所预言的“引力波”为什么恰恰具有光的速度.

10.3.2 GOR波方程的解析

GOR理论，基于“理想逼近”逻辑和“理想代理”法，获得了与爱因斯坦场方程之推迟解(式(10.6))同构一致的GOR场方程之推迟解(式(10.14))，导出了与爱因斯坦波方程(式(10.7))同构一致的GOR波方程(式(10.15))，为我们正确认识爱因斯坦之“引力波”预言提供了理论依据.

那么，GOR场方程之推迟解(式(10.6))和GOR波方程(式(10.15))到底意味着什么呢？

爱因斯坦之“引力波”预言是一个错误！——

GOR场方程之推迟解和GOR波方程意味着：爱因斯坦之“引力波”预言是错误的.

基于其广义相对论导出的波方程，爱因斯坦错误地将光学代理OA(c)传递观测信息的“信息波”当作“引力波”，得出引力波速度即光速的错误结论！

正如第3章3.1.2之“观测局域性”所述，爱因斯坦广义相对论的局域性，是光学观测代理OA(c)之观测上的局域性(c<∞)，而非引力或引力辐射的局域性.爱因斯坦相对论，包括狭义的和广义的，皆光学观测之理论，其观测代理即光学代理OA(c)，其观测信息的传递速度以光速c为限.所以，爱因斯坦场方程推迟积分式(10.6)之所谓“推迟”：|xi-x′i|/c，乃观测信息的推迟，而非引力相互作用的推迟；爱因斯坦波方程(10.7)之波速c乃光学代理OA(c)之“信息波”的波速，而非“引力波”的波速.

如同OR和GOR理论之一切关系式，GOR推迟积分式(10.14)和GOR波方程(10.15)，不仅概括了爱因斯坦推迟积分式(10.6)和爱因斯坦波方程(10.7)，而且概括了牛顿万有引力论之对应关系式.

OA(η)为OA(c)时，η→c，GOR推迟解(10.14)约化为爱因斯坦推迟积分式(10.6)；而OA(η)为OA∞时，η→∞，GOR推迟积分式(10.14)约化为牛顿积分式，观测上的局域性随之消失：

(10.16)

其中，观测信息不再“推迟”.

OA(η)为OA(c)时，η→c，GOR波方程(10.15)约化为爱因斯坦之波方程(10.7)；而OA(η)为OA∞时，η→∞，GOR波方程(10.15)约化为牛顿万有引力定律之泊松方程的真空形式，即拉普拉斯方程：

即

(10.17)

其中，引力相互作用之信息的传递无须时间.

式(10.17)具有重要寓意：第一，隐喻着理想观测代理OA∞之信息波速度无穷大；第二，表明牛顿万有引力定律中的引力相互作用乃理想化的超距作用，引力辐射速度无穷大.

GOR理论并不怀疑引力辐射或引力波的存在.

然而，作为一种客观的物质相互作用形式，引力或引力辐射不会依赖于观测代理OA(η)，更不会依赖于OA(η)之观测媒介传递观测信息的速度η.

GOR波方程的重要意义——

GOR场方程之推迟解和GOR波方程的意义不仅仅在于其证明爱因斯坦“引力波”预言是错误的.

正如第1章所述：“人类对客观世界的认识，既依赖于观测，又制约于观测.”然而，我们至今未能真正地认识到观测和观测媒介在物理学及其理论体系中所扮演的角色及其特殊地位.

OR理论从时间定义这一最基本的逻辑前提出发，导出广义洛伦兹变换，概括统一了伽利略变换和洛伦兹变换[2-3]，由此发现，伽利略- 牛顿理论和爱因斯坦理论，皆为局部理论，依赖于并且制约于各自的观测体系和观测条件：伽利略- 牛顿理论乃理想观测理论，依赖于并制约于理想观测代理OA∞；而爱因斯坦相对论则为光学观测理论，依赖于并制约于光学观测代理OA(c).这意味着，物理学之理论体系或其数学模型中，除了观测者和被观测对象之外，还隐喻着一个特殊并且重要的角色：“观测代理”，通过其观测媒介或某种物质波向观测者传递被观测对象的信息.

于是，OR理论建立了“信息波”的概念——所谓“信息波”，即观测代理传递观测信息的物质波，比如，水波、声波、光波、引力波.不同理论体系，观测代理不同，借助不同的观测媒介，其传递观测信息的“信息波”会有不同的速度：理想代理OA∞之“信息波”的速度无穷大；光学代理OA(c)之“信息波”即光波，速度自然为光速.

那么，物理学之理论体系或其数学模型中，真地隐喻着，需要或存在观测代理，需要或存在为观测者传递观测信息的“信息波”吗？

GOR场方程之推迟解(式(10.14))和GOR波方程(式(10.15))的重要性和价值正在于此.

GOR场方程之推迟解(式(10.14))证明：

物理学之任意理论体系中，的确隐喻地存在着特定的观测代理OA(η)，借助特定的观测媒介，以特定的速度η，为观测者传递被观测对象之信息.

GOR波方程(式(10.15))证明：

物理学之任意理论体系，其观测代理OA(η)之观测时空X4d(η)中，的确隐喻地存在着一种波，那就是OA(η)传递观测信息的“信息波”.

原本，“观测代理”和“信息波”乃OR理论杜撰的概念，现在，却得到了GOR理论的证明；而“信息子”作为构成“信息波”的物质粒子，作为传递观测信息的媒介子，也就具有了其存在的合理性.

爱因斯坦波方程的重要意义——

GOR波方程概括了爱因斯坦波方程.

OR和GOR理论反复强调：伽利略-牛顿理论，乃理想观测条件下的理论，归属理想观测代理OA∞，其观测媒介或“信息波”传递观测信息的速度η被理想化地设定为无穷大(η→∞)；而爱因斯坦相对论，包括狭义的和广义的，乃光学观测条件下的理论，归属光学观测代理OA(c)，其观测媒介为光或光子，其“信息波”即光波，其传递观测信息的速度η自然是光速(η=c).然而，这似乎只是OR和GOR理论的一种主张，而非逻辑和理论之结论.爱因斯坦波方程的重要意义恰在于其从理论上证明了这一主张.

GOR波方程已经证明，爱因斯坦波方程中的波，并非“引力波”，而是光学代理传递观测信息的“信息波”——光波，其速度自然是光速.

爱因斯坦场方程之推迟解(式(10.6))是GOR场方程之推迟解(式(10.14)的一个特例；而爱因斯坦波方程(式(10.7))则是GOR波方程(式(10.15))的一个特例.爱因斯坦场方程之推迟解和爱因斯坦波方程虽然不能预测引力波，却从理论上证明了一个重要的逻辑结论：爱因斯坦的理论，包括其狭义相对论和广义相对论，是光学观测之理论，其观测代理即光学代理OA(c)，其描述的物理过程的确存在着传递观测信息的“信息波”——光波.

10.4 重新诠释LIGO之引力波

GOR理论已经证明，爱因斯坦做出的“引力波”预言是一个错误.那么，LIGO探知的“引力波”又是什么呢？或者，“引力波”真地存在吗？

GOR理论并不怀疑“引力波”的存在：在GOR理论中，“引力波”，即引力辐射之波.

LIGO声称其探测到引力波，并且为此获得了2017年度诺贝尔物理学奖.然而，LIGO的“探测”并非实证之严格意义上的观测和实验.如10.2所述和图12所示，LIGO之“探测”，一半是“听”一半是“猜”，半实半虚.唯一能确定的是，LIGO的确“听”见了某种物质体系发出的“啁啾”之声；至于双星或双黑洞并合，那只是LIGO的臆想，是计算机模拟的结果，属“虚拟现实”，未必真实存在.

猜测即意味着LIGO得出的结论可能是错误的！

GOR理论将为我们重新诠释LIGO系统之引力波探测的原理；而GOR理论之波方程，则将为我们重新鉴别LIGO之GW引力辐射信号，重新鉴别GW之宿主或引力场源，注入新的见解.

10.4.1 基于GOR理论诠释LIGO原理

关于LIGO探测引力辐射或引力波的原理，GOR理论与爱因斯坦广义相对论有不同的观点.

如10.2所述，LIGO之探测原理源于Pirani方案.Pirani[108]基于爱因斯坦广义相对论认为：引力辐射或引力波会导致空间伸缩；测试2个质量体间距的变化，即可探测掠过测试质量的引力辐射或引力波.Weber[109]则进一步认为：空间伸缩会拉伸或挤压物体，令物体伸缩；测定物体的伸缩，即可测定空间的伸缩.在Weber方案中，空间伸缩与物体伸缩是等效的.

LIGO沿袭了Pirani的思想.如10.2.3所述和图11(a)所示，LIGO探测器之体系结构参照迈克尔逊干涉仪设计，其核心是相互垂直的2个激光臂(X和Y)，利用其激光干涉效应测定空间的伸缩.

需要指出：原本，爱因斯坦广义相对论所主张的是4d时空的“弯曲”，而非3d空间的“伸缩”.

基于GOR理论，物质分布或引力场的存在也会导致LIGO激光干涉仪之X-光臂和Y-光臂中2束激光呈现光程差，进而，产生干涉效应.然而，那并非时空“弯曲”或空间“伸缩”所致，而是因为激光在引力时空中的速度发生了变化或摄动.

第6章之6.2基于“理想代理”法获得了球对称引力时空之GOR场方程的解及其线元公式(6.32)：

ds2=(1+2χ/η2)η2dt2-
(1+2χ/η2)-1dr2-r2dθ2-r2sin2θdφ2

式中：η为观测代理OA(η)之“信息波”速度；χ= -GM/η2为引力势，M为引力质量(也代表引力中心).

特别注意：实际上，LIGO探测器是一个光学观测系统，借助激光干涉仪测定2束相互垂直的光束之光程差，进而感应光速的变化.因此，与迈克尔逊- 莫雷实验中的迈克尔逊干涉仪一样，LIGO探测器之观测代理OA(η)即光学代理OA(c).

假定被观测对象m为光子.根据GOR理论，OA(η)为光学代理OA(c)时，其光子m之线元ds=0(这与爱因斯坦广义相对论是一直的).考虑球对称引力时空各向同性，成立：dθ=0和dφ=0.

于是，线元公式(6.32)约化为

0=(1+2χ/c2)c2dt2-(1+2χ/c2)-1dr2

即

(10.18)

式中v为光子m在引力时空中的速度.

式(10.18)表明：光或光子在引力时空中的速度不同于其在真空中的速度c；并且，不同的引力势χ，不同能量的引力辐射或引力波，光或光子的速度会有所不同.当引力场或引力辐射侵入LIGO时空时，特别地，当其导致LIGO激光干涉仪X-光臂和Y-光臂周围时空之引力场或引力辐射非对称时，X和Y两束激光的速度将会有所不同.如此，LIGO激光干涉仪之X和Y两束激光将会呈现光程差并产生干涉效应.

此即GOR理论诠释的LIGO之基本原理：

LIGO探测器，借助激光干涉仪可探知激光之速度摄动，由此，探知引力或引力波，探知引力辐射，探知引力场，进而，探知作为引力源的物质体系.

10.4.2 LIGO之引力波与引力源质量

LIGO欲探测来自太空深处的引力波，需要作为引力源的天体或星体具有巨大的质量.

如10.2.4所述，地球大海本身就是一个引力波天文台，可探测来自天体的引力辐射或引力波：大海因感应月亮和太阳之引力辐射或引力波而呈现潮汐现象.基于牛顿万有引力定律的理论推导，地表之单位质量的物质或海水，其感应的引潮力FT，与引力源之质量M成正比，与引力源之距离d的立方成反比：

(10.19)

式中：G为万有引力常数；r为地球半径；Δm为地表物质单位质量；aT为等效加速度.

LIGO本身也是“地表物质”体系.

或许，式(10.19)具有重要的启示性意义：地球表面任意引力辐射探测器或引力波探测器，包括大海和LIGO，均制约于引力源距离之“立方反比律”.式(10.19)意味着，地表之引力波探测器，无论LIGO还是大海，能否探测到引力辐射或引力波，很大程度上取决于引力源与引力波探测器的距离.

太阳质量是月亮质量的2 711.2万倍；而太阳与地球的距离则是月亮与地球距离的390.6倍.依式(10.19)计算可知：太阳的引潮力加速度为5.05×10-7m/s2；而月亮的引潮力加速度为1.10×10-6m/s2，是太阳的2.18倍.这意味着，至少还需要增加1个太阳的质量，太阳引潮力才能达到与月亮相当的引潮效应.

距离地球最近的恒星，比邻星，质量约0.12个太阳，距离地球约4.22光年.依式(10.19)计算，其质量M须达到约1.88×1016个太阳，其对地球大海或LIGO探测器的引潮力才能达到与太阳相当的引潮效应：

(10.20)

比邻星，即使其质量如此巨大——达到1.88×1016个太阳，也未必能触发LIGO探测器.如10.2.4所述，就LIGO探测器及其周围时空而言，类同于月亮和太阳之情形，相对静止的比邻星，其引力场近似于静态引力场，难以令LIGO探测器之X-光臂和Y-光臂中的2束激光形成足够的光程差并产生干涉条纹.

LIGO之第一个引力波探测信号GW150914，其虚构的引力波源乃一双黑洞天体，总质量仅约67个太阳，距离地球约13亿光年.如此遥远的天体需要多少太阳堆积在一起才能对地球大海或LIGO探测器产生相当于太阳的引潮效应呢？即使考虑双黑洞并合我们也无法想象LIGO探测器怎么能探测到来自那么遥远的引力波.

令我们好奇的是，GW150914能触发LIGO探测器，是否也应该能触发地球之大海而形成潮汐呢？

10.4.3 LIGO之引力波与双黑洞

在其O1和O2以及O3a+b三期探测活动中，LIGO探知的引力辐射信号共91例，全部匹配上双星并合模型，其中，绝大部分是双黑洞(84例)，个别为双中子星(2例)，或一黑一中天体(5例).

实际上，如10.2.4所述，LIGO从一开始便将其引力波探测目标定向于双星并合，特别地，指向双黑洞并合.然而，无论中子星还是黑洞，无论双中子星系统还是双黑洞天体，无论双中子星并合还是双黑洞并合，都只停留在假设性的理论或数学模型中，停留在计算机虚拟现实的模拟计算中.

宇宙真地存在双黑洞天体，并且，经常性地发生双黑洞并合事件吗？是宇宙真地存在双黑洞还是LIGO探测引力波需要双黑洞？

LIGO之双黑洞的由来——

1967年，射电天文望远镜探测到周期性电磁脉冲信号，人们由此猜想，宇宙存在脉冲星；进而认为，脉冲星就是“中子星”(一种几乎已经被人们抛弃的存在于理论设想的虚构天体)[112-114].设想的中子星质量巨大，然而，如10.4.1所述，并不足以生产LIGO所需要的高能引力波.

1974年，射电天文望远镜探测到周期呈周期性变化的电磁脉冲信号，人们由此猜测，宇宙存在脉冲双星[115-116]；进而认为，双星椭圆轨道半长轴和轨道周期会逐渐缩短，最终并合[117-118].双中子星并合必定剧烈地爆炸，或许，能喷发高能引力波.然而，中子星质量有限，即使双中子星并合，其辐射的引力波之能量可能依然不满足LIGO的需求.

于是，物理学家们脑洞大开[123-124]，想到了黑洞，构思了双黑洞天体及其可能发生的并合.黑洞的质量可以随意地设想，如此，双黑洞并合则可喷发任意高能之引力波.

从中子星到脉冲星，从脉冲星到脉冲双星，从脉冲双星到双中子星并合，再由双中子星并合到双黑洞并合，似乎一切都建立在猜测和假象的基础之上.至今，除了计算机仿真或计算机模拟，没有任何关于双黑洞天体及其并合的实证依据.

实际上，并非LIGO“听”到的“啁啾”之声真地源于双星或双黑洞并合.

LIGO的套圈游戏——

如10.2.5所述，宇宙对于人类还有许多的未知；LIGO探知的每一例引力辐射信号GW都意味着无限多的选项或可能.然而，LIGO从一开始便将其探测目标定向于双黑洞.LIGO鉴别其探知的引力辐射信号GW很有些像街头的套圈游戏.

LIGO之O1和O2以及O3a+b三期探测活动中探知的91例GW引力辐射信号，仅有2例匹配上双中子星并合模型：GW170817和GW190425，相对于双黑洞模型，距离地球较近，其中，GW170817为1.3亿光年，而GW190425为5.2亿光年.或许，正是因为它们距离地球较近，匹配质量不能过大，达不到黑洞量级，只能匹配中子星.有人对GW190425的归类看法不同：GW190425距地球较GW170817远，其匹配的质量较大，近乎黑洞.LIGO探知的GW引力辐射信号，是否匹配双黑洞或双中子星，取决于它们与地球的距离.

特别令人困惑的是：似乎LIGO之双黑洞不能距离地球太近——如果太近，则LIGO之双黑洞会变成双中子星；并且，距离地球越远，LIGO之双黑洞就会越“黑”，总质量就会越大.

LIGO之双黑洞的存在，或LIGO之双黑洞的并合，依赖于双黑洞与地球的距离.LIGO数据中的这一现象究竟意味着什么呢？

LIGO之双黑洞模型的误区——

以图12和表3中的GW150914为例：一方面，LIGO基于其双黑洞动力学模型的计算机模拟，声称其探测到的GW150914即爱因斯坦所预言的“引力波”，从而证明了“引力波”的存在；另一方面，LIGO又基于其探测到的GW150914，声称其探测到双黑洞及其并合事件，从而证明宇宙存在双黑洞天体，并且，双黑洞最终将并合.

如此的循环论证，逻辑上，颇值得怀疑.

依据LIGO的计算机模拟，GW150914之双黑洞并合后损失约3个太阳质量；依据爱因斯坦公式E=mc2，这些质量以“引力波”的形式转化为双黑洞并合时向外喷发或辐射的能量.

然而，其中存在诸多误区和疑点.

首先，LIGO的双黑洞模型乃“数值相对论”的产物，以爱因斯坦的狭义相对论和广义相对论为基础.然而，LIGO并未意识到，爱因斯坦的理论乃局部理论，属光学观测理论，仅在光学代理OA(c)下成立；OR和GOR理论已经阐明，爱因斯坦相对论之物理量皆光学观测物理量，包含着OA(c)之观测效应.我们很难确定，LIGO是否将其基于爱因斯坦相对论的理论模型限定在光学观测条件之下.同时，我们也很难想象LIGO依据什么能得出GW150914之双黑洞并合过程有3个太阳质量转化为“引力波”.

其次，LIGO错误地将爱因斯坦公式E=mc2用于计算双黑洞并合可能喷发的引力波能量.OR理论[1-3]已经阐明：爱因斯坦公式E=mc2只是OR能量公式E=mη2之特例，仅当观测代理OA(η)为光学代理OA(c)时成立；E=mc2仅代表物体m以光速运动时的OA(c)观测动能，并不意味着质量m可以转化为能量.正如核爆炸所辐射出的能量，是禁闭于原子核内之能量的释放，而非质量转化而来.因此，LIGO基于爱因斯坦公式E=mc2计算双黑洞因并合而喷发的“引力波”辐射能，理论上，是错误的！

同时，LIGO错误地将普朗克方程E=hf用于计算引力辐射或引力波GW信号的能量.第一，关于频率f：LIGO探知的GW信号，其频率并非引力辐射或引力波的频率，而是X和Y两束激光之速度相对摄动的频率，并且，依赖于激光频率；第二，关于普朗克常数h：OR理论[2-3]阐明，h乃光学代理OA(c)之普朗克常数，根据广义普朗克方程(式(2.20))，不同观测代理OA(η)有不同的普朗克常数hη(式(2.22)).基于普朗克方程E=hf的量子理论，与爱因斯坦广义相对论一样，皆光学观测理论，仅当观测代理OA(η)为光学代理OA(c)时成立.因此，LIGO基于普朗克方程E=hf计算其探知的GW引力辐射信号或引力波信号所具有的能量，理论上，也是错误的！

另外，双黑洞并合必定无比剧烈地爆发，并且，无比剧烈地向外喷发物质；而辐射的能量皆由其喷发的物质所携带，而非由其喷发的物质所转化.如10.2.6所述，如果宇宙真地存在双黑洞并合，那么，不仅可能喷发引力辐射或引力波，还可能喷发电磁物质，以及任何其他物质.例如，LIGO探测到第一例引力波信号GW150914之后仅仅0.4 s，Fermi GBM便探测到了来自同一天区的伽马射线暴[141-142]；如果GW150914真地源于双黑洞并合，那么，这一伽马射线暴则可视为双黑洞并合后喷发的电磁物质.实际上，即使宇宙真地存在双黑洞，即使双黑洞真地会并合，其喷发的能量中，引力辐射或引力波也可能只占极小的部分，难以满足LIGO探测器对来自深空之引力波的高能需求.

可见，LIGO将触发LIGO探测器的GW信号诠释为来自双星并合后喷发的“引力波”，既缺乏足够的实证依据，同时，也缺乏足够的理论依据.

10.4.4 LIGO之引力波的速度问题

如之前所述，引力和引力波的存在无须证明.关于爱因斯坦之“引力波”预言，重要的不是引力波是否存在，而是引力波速度是否为光速.

GOR理论已经证明，爱因斯坦预言的所谓“引力波”，其实，并非物质体系辐射的引力或引力波，而是光学代理OA(c)传递观测信息的“信息波”.光学代理OA(c)传递观测信息的“信息波”即光波，其速度自然为光速；然而，那不是引力波的速度.

那么，真正的引力辐射或引力波之速度呢？

毫无疑问，依局域性原理，引力非超距作用.因此，引力辐射或引力波，其速度必定是有限的.

然而，引力辐射或引力波，其速度未必是光速.

实际上，观测和实验似乎更倾向于支持拉普拉斯和Flandern等的观点及其得出的结论[22，56，143-144]：引力波的速度远远大于光速——如果引力波的速度为光速，那么，我们的宇宙将失去现有的稳定结构.只因有悖于爱因斯坦广义相对论和爱因斯坦之“引力波”预测，这类观点未能得到主流物理学界采信.

一个显而易见的事实是：黑洞之所以“黑”，是因为光波或光子不够快，受黑洞之巨大的引力束缚，无法逃离黑洞；然而，黑洞却不能束缚引力波或引力子，否则，黑洞将会失去其与外部物质体系的引力相互作用，如此，LIGO所设想的双黑洞体系将无法存在：2个黑洞将无法相互吸引或相互环绕，自然地，也不会有双黑洞并合的事件发生.由此可见，引力子或引力波的速度或许真如拉普拉斯和Flandern预测的那样，大于甚至远远大于光速.

LIGO声称其探测到“引力波”；并且，正如10.2.6所述，基于“三边测量法”和“多信使天文学”联合探测之观测数据，LIGO还声称其证明：“引力波”速度即光速[139].实际上， LIGO并未真正地测定引力波速度.即使借助多基站和多信使，LIGO仍然不能对其引力波源进行准确定位，因此，其“三边测量法”难以准确测定引力波速度.LIGO的Livingston基站和Hanford基站相距3 002 km，约10 ms光程.GW 150914掠过LIGO之双基站，耗时约7 ms.对此，LIGO只能得出极为模糊的结论：GW150914的速度符合爱因斯坦预言：引力波以光速传播.

GW170817是LIGO的第一列也是少有几例匹配上双中子星并合模型的引力波信号，前后伴随了诸多电磁物质团块，包括伽马射线暴GRB170817A.最终，LIGO设想GW170817和GRB170817A由同一双中子星于同一并合时刻出发并且同时抵达地球，前后仅相差约1.7 s；以此为据，间接地论证或证明：引力波速度与光速c精确地相符(式(10.8))[139].

那么，引力波之速度真地等同于光速吗？

问题在于：引力波GW170817和伽马射线暴GRB 170817A真地源于同一双中子星并合事件吗？

毫无疑问，伽马射线暴GRB170817A来自某个天体，或许，恰好就是LIGO通过计算机模拟匹配上的双中子星：距地球0.85亿光年，总质量3个太阳，并且，于0.85亿年前并合，其喷发或辐射出的伽马射线暴GRB170817A以光速旅行0.85亿年后来到地球.

然而，引力波GW170817不是.

其实，LIGO并不确定双中子星或双黑洞天体是否真实地存在；即使其存在，LIGO也不确定其是否会并合；即使其并合，LIGO也不确定其并合后能喷发多少能量；即使其喷发的能量可基于理论计算，LIGO也不确定其中多少能量属于引力辐射或引力波.实际上，无论双星系统是否真地存在，无论双星或双黑洞是否真地会并合，LIGO探知的所有引力辐射信号GW皆与双星或双星并合无直接关系.LIGO所“听”见的，并非双中子星或双黑洞并合时发出的“啁啾”之声，而是类同于GRB170817A的电磁物质体系在LIGO探测器附近的“鸣叫”.

LIGO错误地将电磁物质之引力场随电磁物质体系移动的速度当作引力辐射或引力波的速度.

具有讽刺意味的是，正是LIGO关于引力波速度即光速的论据[139]，将为我们揭示LIGO探知的GW引力辐射信号或引力波信号之实质和根源.

10.4.5 LIGO究竟探测到了什么？

LIGO声称其探测到了引力波，证明了爱因斯坦之“引力波”预言：引力波不仅存在，并且，恰如爱因斯坦所预言的，引力波速度即光速！

然而，GOR理论已经证明，爱因斯坦之“引力波”预言是一个错误：爱因斯坦波方程(式(10.7))中的波，并非“引力波”，而是其光学代理OA(c)传递观测信息的“信息波”.无论LIGO是否真地探测到了引力辐射或引力波，无论LIGO探知的引力辐射或引力波之速度是否真地为光速，都不意味着爱因斯坦正确地做出了关于“引力波”及其速度的预言.

那么，LIGO真地探测到了引力辐射或引力波吗？引力辐射或引力波的速度真地是光速吗？

LIGO探测器的触发条件——

根据GOR诠释，LIGO是一个万物探测器.

电磁物质携带电磁场，辐射电磁波；射电望远镜能感知电磁场，感知电磁辐射或电磁波，因此，可谓“电磁物质探测器”.一切物质体系皆具有质量，携带引力场，辐射引力和引力波；LIGO探测器能感知引力场，感知引力辐射或引力波，因此，可谓“万物探测器”：能探测宇宙之一切物质.

只要有物质侵入或掠过LIGO时空，其携带的引力场即可能触发LIGO探测器.然而，物质体系之引力场触发LIGO探测器必须具备2个条件.

第一，具备足够的引力场强g=GM/r2.要求：质量M足够地大；或者距离LIGO探测器足够地近(r足够小).

第二，X-光臂和Y-光臂所感应的场强各异.要求侵入的引力场非均匀非对称非等势.

LIGO的确探测到了引力波——

基于GOR理论之诠释：引力波，即引力辐射之波.在此意义上，LIGO的确探测到了引力波！

基于GOR理论所诠释的LIGO探测器之基本原理，触发LIGO探测器的GW信号，从GW150914到GW200322，的确意味着有物质体系及其引力场侵入或掠过LIGO时空，导致其F-P真空腔之激光速度摄动，X和Y两束激光呈现光程差，激光干涉仪产生干涉条纹和干涉效应，由此触发了LIGO探测器.

可以确定：LIGO的确探测到了某种物质体系的侵入和袭扰，的确探测到了某种引力场，的确探测到了引力辐射或引力波.然而，这并不意味着触发LIGO的GW信号源于双星或双黑洞并合.

同时，还可确定：LIGO探知的引力辐射或引力波并非直接来自双星或双黑洞并合；并且，LIGO探知的引力辐射或引力波，其速度并非光速.

LIGO之引力波并非源于双星并合——

双星或双黑洞天体，即使其存在，即使其并合，也难以满足LIGO探测器的触发条件.

首先，如10.4.1所述，双星或双黑洞天体虽然质量巨大，却距离地球遥远，其引力场之场强随距离依平方反比律衰减，掠过地球时，其引力场已经难以触发LIGO探测器.

其次，如10.4.2所述：1)双星或双黑洞之并合所能喷发的能量，只能由其喷发的物质携带，而非质量转化而来，总能量远低于LIGO之计算机模拟计算量，并且，引力辐射能量或引力波能量只能占其中极小的部分；2)并合所喷发的引力辐射应近似球面波，其能量密度同样地随距离依平方反比律衰减；3)掠过地球时，其球面波相对于LIGO之X-光臂和Y-光臂近似均匀对称等势.因此，双星或双黑洞并合同样地难以触发LIGO探测器.

LIGO之引力波速度貌似光速的寓意——

LIGO声称，其探知的引力辐射或引力波之速度等同于光速.先是，LIGO依据其引力辐射信号掠过其双基站的用时，基于图11(b)所示的“三边测量法”得出了引力波速度与光速近似相符的结论：例如，GW150914用时7 ms，GW170814用时6 ms，GW170817用时3 ms；而LIGO之Livingston基站和Hanford基站相距3 002 km，光程约10 ms.之后，LIGO又依据GW170817和GRB170817A由同一双中子星于同一并合时刻出发，并且，几乎同时抵达地球，“证明”[139]：引力波速度与光速精确相符(式(10.8)).

那么，LIGO探知的引力辐射信号，其速度为什么会貌似光速？LIGO关于引力辐射速度或引力波速度等同于光速的判断究竟意味着什么呢？

事实上，LIGO探知的引力辐射信号及其记录的探测数据并不能证明引力波速度即光速；只意味着：

有引力辐射袭扰LIGO探测器；

引力辐射源或引力场源以光速移动，而非引力辐射以光速传播.

如图13所示，LIGO探测到的引力辐射或引力波信号，从GW150914到GW200322，其宿主或其引力场源，并非双星或双黑洞，而是电磁物质.

图13 为什么电磁(EM)物质总会伴随LIGO之引力波？ Fig.13 Why does electromagnetic matter always accompany the gravitational waves of LIGO?

电磁物质为什么伴随LIGO之引力波？——

如图13(a)所示，在LIGO之引力波联合探测活动中，每当LIGO探测到引力辐射或引力波之时，总会发现，其前后左右有电磁物质的身影，所谓“电磁伴随物”，意即伴随引力波的电磁物质，包括伽马射线暴和X射线，以及其他频段的电磁物质.

电磁物质掠过地球的事件是极为常见的；而双星或双黑洞及其并合的事件却是前所未有的.

其实，并非电磁物质伴随着LIGO探知的引力辐射或引力波，而是电磁物质携带着引力场，辐射引力或引力波，并且，近距离地触发LIGO探测器.

根据OR理论，一切物质，包括电磁物质，皆具有质量，携带引力场，辐射引力和引力波.

任意物质体系之引力场随其物质体系移动.以地球为例，地球以3×104ms-1的速度在环绕太阳的轨道上移动；自然地，地球之引力场随地球以3×104ms-1的速度移动；然而，这并不意味着引力辐射的速度为3×104ms-1.同样，电磁物质以光速移动；自然地，电磁物质之引力场以光速随电磁物质移动；然而，这并不意味着引力辐射或引力波的速度即光速.

电磁物质，如图13中的电磁物质团块(LIGO之引力辐射的“电磁伴随物”)，是由电磁粒子(光子)构成的，可称之为“电磁粒子团”(electromagnetic particle cluster, EPC)，以光速运动.OR理论已经阐明，光子具有“静止质量”，也就是光子的“固有质量”.如此，作为物质体系，电磁粒子团必定携带引力场，辐射引力和引力波.特别地，电磁粒子团之引力场，必定以光速随电磁粒子团移动.

如图13(b)所示，基于“三边测量法”的计算显示，LIGO探知的引力辐射信号掠过LIGO双基站的速度与光速相符.然而，特别值得注意：这并不意味着引力波的速度即光速；这只意味着，LIGO探知的引力辐射信号，其宿主或其引力场源以光速运动.

那么，LIGO探知的引力辐射信号，其宿主或其引力场源究竟是什么样的物质呢？

LIGO之引力波真正的宿主：EPC——

一切都指向了以光速运动的电磁物质！

LIGO探知的引力辐射或引力波，其宿主，原本就是电磁物质；有电磁物质伴随，似乎，是合理的.

LIGO之引力波探测器的确探测到引力场，探测到引力辐射或引力波.然而，无论其引力场，无论其引力辐射或引力波，皆非源于双星或双黑洞，也非双星或双黑洞之并合，而是电磁物质.

如图13(c)所示，电磁粒子团，虽然质量极小，却能近距离地掠过或袭扰LIGO探测器.当电磁粒子团近距离地掠过LIGO探测器时，当其引力场或引力辐射非对称地袭扰LIGO之X-光臂和Y-光臂周围时空时，满足物质体系之引力场触发LIGO探测器所需具备的条件，因而，可触发LIGO探测器.

如此，我们可以合理地做出如下基本判断.

一个基本判断：LIGO的确探测到引力辐射或引力波；然而，LIGO所探知的GW引力辐射信号，并非直接源于双星或双黑洞，也非双星并合或双黑洞并合，而是掠过地球并且近距离袭扰LIGO探测器的电磁物质，或许，正是被LIGO视为GW之“电磁伴随物”的众多电磁粒子团中的成员——或伽马射线暴，或X射线，或者，其他频段的电磁物质.

LIGO所探知的，并非遥远双星或双黑洞并合而喷发的引力波，而是电磁粒子团掠过地球和LIGO探测器时近距离的引力辐射.LIGO探知的引力场，其宿主或引力场源，并非双中子星或双黑洞，而是电磁粒子团.如此，可将LIGO引力辐射信号GW之引力场源记作EPC：GW150914的引力场源即EPC 150914.伴随GW同时抵达地球的电磁物质常被称作GW之“电磁对应体”(EM counterpart)；其实，GW真正的电磁对应体应该是EPC：GW170817的电磁对应体是EPC170817，而非GRB1708017A.

LIGO探知的引力辐射信号GW，其电磁对应体EPC，必定源于宇宙深空某电磁辐射源.电磁粒子团EPC170817是LIGO探知的引力辐射信号GW170817的宿主或引力场源；GRB170817A则是Fermi GBM和INTEGRAL探知的伽马射线暴.二者同源的可能性极大：EPC170817和GRB170817A同为电磁物质，来自同一天区，并且，几乎同时地抵达地球，前后仅相差1.74 s；设想其同源且同时出发，自然是合理的.

LIGO和Fermi GBM以及INTEGRAL探知的EPC170817和GRB170817A皆电磁物质.不同的是：Fermi GBM和INTEGRAL通过感应电磁场，探知电磁辐射或电磁波，探知伽马射线暴GRB170817A，乃至其他电磁物质；而LIGO则通过感应引力场，探知引力辐射或引力波，探知电磁粒子团EPC170817，乃至探知万物，包括一切电磁物质.

射电望远镜，基于其观测数据或其观测频谱，识别电磁物质；或许，LIGO也能基于其记录的GW数据或GW频谱识别或解读其电磁对应体EPC.

LIGO欲探测来自非电磁物质之引力场的引力辐射或引力波，或许，还需要加以改进！

10.4.6 合理的诠释和遗留的问题

综合10.4.1～10.4.5之分析，我们可以得出明确的结论：LIGO的确探测到引力辐射或引力波.

然而，LIGO探知的引力辐射或引力波，并非如LIGO臆想或推测的那样来自双星或双黑洞之并合，而是掠过地球并且近距离袭扰LIGO探测器的电磁粒子团EPC，来自EPC之引力场.

LIGO探知的引力辐射或引力波，其速度并非光速，只是作为其引力场源的EPC以光速移动.

如此，一切皆有了合理解释！——

问：为什么LIGO探知的引力波GW掠过LIGO不同基站的速度符合光速？

答：GW之宿主或引力场源是以光速运动的电磁粒子团EPC，自然，其携带的引力场以光速移动.

问：为什么GW170817和GRB170817A几乎同时抵达地球，前后仅相差1.74 s？

答：LIGO探知的引力辐射信号GW170814，其引力场源或其电磁对应体EPC170817，与Fermi GRM和INTERGRAL探知的伽马射线暴GRB170817A同为电磁粒子团，并且，源于同一天区；设想其同时地从同一电磁辐射源出发，以相同速度(光速)同向移动，同时抵达地球是合理的.

问：为什么LIGO探知的引力辐射信号GW常有电磁物质伴随？

答：LIGO探知的引力辐射信号GW，其宿主或引力场源是GW之电磁对应体EPC；作为电磁物质，EPC必定源于深空某个电磁辐射源，其一定时间段内辐射的电磁物质，除GW之电磁对应体EPC外，必定还会有其他电磁物质，伴随EPC同速同向运动.特别需要指出，这些所谓的“电磁伴随物”，其伴随的并非是引力辐射或引力波GW，而是电磁物质粒子团EPC.

问：为什么说触发LIGO探测器的引力辐射或引力波GW，其引力场源或引力辐射源是某种电磁粒子团EPC，而非LIGO推测的双星或双黑洞？

答：10.4.1～10.4.5正是对这一问题的回答.

问：为什么质量极微的电磁粒子团EPC，其引力场能触发LIGO探测器？

答：如图13(c)所示，途经地球的电磁粒子团可以近距离地掠过LIGO探测器(满足LIGO之触发条件一)，并且，其引力场可以非对称地袭扰LIGO之X-光臂和Y-光臂周围时空(满足LIGO之触发条件二)；如此，导致X和Y两束激光呈现速度摄动以及光程差，进而，导致LIGO之激光干涉仪产生干涉条纹或干涉效应，触发LIGO探测器.

电磁物质掠过地球或袭扰LIGO探测器的事件可以实证；而双星或双黑洞并合的事件只能推测.

引力波速度问题依然存在——

LIGO探测到引力辐射信号，某种意义上，可视为是对引力辐射或引力波存在性的一种证明.

无论如何，引力辐射的速度或引力波的速度，既不是牛顿万有引力论所能预测的，也不是爱因斯坦广义相对论和GOR理论所能预测的.最终，引力波的速度，还需要通过观测和实验来测定.

与光速问题一样，引力波速度的理论预测不能替代观测和实验的验证.实验物理学家曾经为光速的测定付出过艰辛而巨大的努力.如今，我们掌握了测定光速的技术，却不知道如何测定引力辐射或引力波的速度.或许，引力波速度的测定需要实验物理学家付出远比光速的测定更为艰辛和更为巨大的努力.

11 GOR理论与宇宙大爆炸

内禀的好奇心促使人类不断地探索自然.

疑难，是智慧的产物.作为智慧生命，人类，自从有了自我意识的那一刻起，便有了基本问题之疑难：我们是谁，我们在哪里？这的确属重大疑难——直到今天我们也不十分清楚我们是谁或我们在哪里.

随着人类思想和认识的进步，随着人类物理学的发展，如今，我们至少已经明白：人类乃太阳系地球之智慧生命；人类并非生存在巨龟的背上，地球不是宇宙的中心，太阳也不是.随之，新的疑难又出现了：地球为什么会围绕太阳运行，宇宙的中心在哪里？牛顿建立万有引力定律[53]，告诉我们，地球受引力作用而围绕太阳运行；爱因斯坦建立广义相对论[14-15]，告诉我们，太阳令时空弯曲，弯曲的时空令地球围绕太阳运行.如此，人们感到很困惑.引力到底存在或不存在？时空到底弯曲或不弯曲？

人类不断地探索自然，旧的疑难尚未得到解答，新的疑难却层出不穷.每当人类的疑难未能得到正确的诠释之时，物理学便会滋生出许多的神话，玄妙深奥，似是而非，甚至，荒诞无稽.

Michelson(迈克尔逊)和Morley(莫雷)[42]发现，光速似乎是不变的：迈克尔逊- 莫雷实验中，光速失去了叠加效应.人们不能理解光速为什么无叠加效应，爱因斯坦也不能.

“光速不变性”可谓现代物理学一大疑难.

既然不能理解，那就叫它“原理”好了.于是，爱因斯坦“制造”了“光速不变性”原理，进而，建立起爱因斯坦相对论，包括狭义的和广义的.爱因斯坦相对论引发了一系列新的疑难，诸如：时涨尺缩、同时性之相对性、时空弯曲，以及光子零质量等问题，难以理解.

爱因斯坦相对论之疑难皆相对论性疑难.

观测相对论揭示了时空和物质运动之相对论性的本质：OR理论阐明了光速为什么不变；GOR理论阐明了时空为什么弯曲.

现代物理学之疑难大多涉及相对论和量子论，自然地，与观测相对论相关，与OR理论或GOR理论相关.表5列载了现代物理学与相对论和量子论相关的重大问题，谓之“物理学疑难”(big puzzle)，供理论物理学家和实验物理学家商榷和审视.表5中，一些问题已由OR理论或GOR理论阐明，却仍需观测和实验的检验或实证；而另一些问题，基于OR理论或GOR理论，或许，能引发新的思考，获得新的诠释.

表5 物理学十五大疑难

表5列载的十五大物理学疑难是现代物理学之基本问题和重大问题；主流物理学界对这些疑难的诠释是大家熟悉的.主流物理学界的观念大多基于爱因斯坦相对论，基于爱因斯坦的视角，基于光学观测或光学代理OA(c)的视角.

现在，我们需要换个视角：基于观测相对论，基于一般观测代理OA(η)之更为广阔的视角，重新审视这些物理疑难和物理学的重大问题，或许，物理学将从中获得新的思想和新的认识.

限于篇幅，这里，仅讨论表5中第十五大疑难：宇宙大爆炸(BP-15).表5中其余疑难(BP-01～BP-14)，有兴趣可参阅文献[145].

11.1 问题陈述

大爆炸(big bang)宇宙论：最初，宇宙所有的物质聚集为一点，密度和温度极高，接近或达到了Schwarzschild球对称时空度规之引力奇点(rs=0)，空间和时间已无意义，时空处于虚无状态；突然，一声巨响(没人听见)，一道耀眼闪光(没人看见)，所有的物质剧烈地向外喷发，新的宇宙就此诞生，时间开始流淌，空间开始膨胀，最终，演化为我们今天看到的宇宙.此即所谓“宇宙大爆炸”.

我们简短地回顾一下大爆炸宇宙论的形成.

1927年，比利时宇宙学家Lemaitre提出了一种学说：很久很久以前，宇宙乃一“太古原子”(primeval atom，依照物质不灭定律，应该集聚了如今宇宙所有的物质，包括其质量和能量)；之后，“太古原子”爆炸，形成了如今的宇宙.1929年，美国天文学家哈勃提出哈勃定律：星系之光谱红移量与星系之间的距离成正比.哈勃由此推论，星系正相互远离而去；此即宇宙膨胀学说，为Lemaitre的宇宙大爆炸学说做了极好的注脚.1946年，美国物理学家Gamow正式地提出大爆炸宇宙论.Gamow建立了热大爆炸(hot big bang)的概念和理论模型：宇宙，在大约140亿年前，由一次大爆炸形成.之后，一番更精细的推算，宇宙诞生的时间被确定为138亿年之前.1964年，Penzias和Wilson发现大爆炸宇宙论预言的宇宙微波背景辐射(cosmic microwave background, CMB)，CMB被视为大爆炸宇宙论之关键证据.

自然地，为了解释宇宙如何从一粒“太古原子”演化为如今的宇宙，时间如何从静止开始流淌，空间如何从原子开始膨胀，大爆炸宇宙论离不开爱因斯坦之广义相对论.在现代广义相对论之大爆炸宇宙论中，Lemaitre的“太古原子”演变成为“引力奇点”，或称“大爆炸奇点”，或称“宇宙奇点”(cosmic singularity).于是，宇宙或时空具有了“柔性”，时间可慢可快，空间可张可驰；如此，时间方能由停滞开始流淌，空间方能由虚无开始扩张.

主流学派对大爆炸宇宙论深信不疑；然而，质疑大爆炸宇宙论的声音也从来没有停顿过.最简单的问题往往是大爆炸宇宙论最难以回答的问题.

宇宙真地需要一个起点吗？“太古原子”是静止的还是运动的？如果静止，那么，它不会爆炸；如果运动，那么，它的时间不会停滞，空间不会只是rs=0的引力奇点.依照现代广义相对论的逻辑，宇宙的时间由停滞开始流动，时间流淌速度应该存在一个从无到有和从慢到快的过程；那么，大爆炸宇宙论之宇宙演化过程中，为什么时间从古至今的节律始终如一呢？宇宙巨量的物质真地能挤压成一粒“太古原子”吗？大爆炸之前，宇宙一直就是一粒“太古原子”吗？有人设想，应该给予爱因斯坦场方程一个合适的“宇宙常数”，以便宇宙或时空能周而复始地由大爆炸开始膨胀，膨胀速度由快变慢，然后，开始收缩，直至其达到新的“宇宙奇点”，迎来新一轮的宇宙大爆炸.可是，物质聚集后一定会爆炸吗？宇宙为什么要整个地收缩至一粒“太古原子”或“宇宙奇点”才爆炸呢？Weinberg[146]曾说：“一种可能是，宇宙从来就没有真正达到过密度无限的状态.宇宙现在的膨胀可能始于从前一次收缩的末尾，当时，宇宙的密度达到了一个非常高的但仍然有限的状态.”那么，物质究竟应该达到一个什么样的高密度状态才会爆炸呢？银河系内所有恒星能量耗尽之后，其物质坍缩并挤压在一起会导致大爆炸吗？如果会，那么，这将意味着一个新的宇宙诞生了吗？如果是，那么，超新星爆意味着新的宇宙诞生了吗？一般黑洞虽不如“太古原子”那么“黑”，依照现代广义相对论之逻辑，当其“黑”到一定程度也可能会发生爆炸.那么，一般黑洞的爆炸意味着新的宇宙诞生了吗？

我们无法继续设想下去，那会越发地荒谬.

“宇宙奇点”，或宇宙大爆炸之前的“太古原子”，可谓最大的黑洞.如果Mersini-Houghton[147-148]关于“黑洞不存在”的理论或结论成立，那么，大爆炸宇宙论或将无法成立.其实，Mersini-Houghton的理论，正如BP-14所述，与现代广义相对论之黑洞理论一样，是基于现代广义相对论和量子引力论的.因此，Mersini-Houghton对黑洞理论的质疑，无关黑洞理论或大爆炸宇宙论是否正确；只意味着：现代广义相对论，逻辑上，缺乏一致性和自洽性！

实际上，根据GOR理论，无论爱因斯坦广义相对论或现代广义相对论，只是光学观测之局部理论，以其为基础的大爆炸宇宙论难以成立.

此即物理学疑难之BP-15.

11.2 主流学术界的观点

现代广义相对论之大爆炸宇宙论代表着主流物理学界对宇宙大爆炸和宇宙演化所持的观点或认识.

主流物理学界认为：宇宙诞生之前，时空和物质蜷缩至一个奇点，所谓“引力奇点”或“宇宙奇点”，时空曲率无穷大(时空无限弯曲)，时间停滞，空间归零；物质密度无限大，温度无限高.大约138亿年前的某一刻，宇宙在奇点爆炸，时间开始流淌，空间开始膨胀，直至演化成为如今的宇宙.

此即大爆炸宇宙论.

大爆炸宇宙论之基本前提有2项.

第一，普适原理：物理学定律具有普遍适用性；

第二，宇宙学原理：大尺度上，宇宙是均匀的和各向同性的.

大爆炸宇宙论之理论基础涉及：

第一，爱因斯坦广义相对论；

第二，量子引力论.

支持大爆炸宇宙论的主要观测证据包括：

第一，宇宙红移——哈勃定律及其宇宙膨胀学说；

第二，CMB——宇宙微波背景辐射；

第三，轻元素或原生元素的丰度值.

宇宙大爆炸论之简史如下.

量子引力时代(0～10-44s)：虚时空大爆炸，温度∞.

普朗克时代(10-44～10-36s)：5.4×10-44s开始超统一相变，实时空(真空场)形成，物质粒子产生(轻子和夸克不可分)，相变温度1032K.

大统一时代(10-36～10-32s)：10-36s开始大统一相变，暴胀，正反物质非对称，夸克与轻子分离，相变温度1028K.

夸克- 轻子时代(10-32～10-6s)：10-12s开始电弱统一相变，相变温度1016K.

强子- 轻子时代(10-6～1 s)：夸克禁闭，10-6s强子产生，温度1012K；10-4s开始轻子及其反粒子占主导地位，温度1011K.

辐射时代和核合成时代(1 s～2×105a：正负电子湮灭，1 s开始进入辐射时代，4 s～30 min氦核形成，温度1010K；光子退耦，2×105a开始氢原子形成，温度4 000 K.

星系时代(2×105～109a)：原始星系和星系形成.

恒星时代(109～5×109a)：恒星产生，重元素形成，行星出现，分子形成.

现在时代(5×109～1.5×1010a)：人类观测到宇宙膨胀和3K宇宙背景辐射，并依据爱因斯坦广义相对论和粒子物理学建立宇宙模型.

现代广义相对论之大爆炸宇宙论中的宇宙模型，宇宙的年龄甚至可精确到(137.99±0.21)亿a.真地难为了大爆炸宇宙学家：他们居然能构思或制造出如此富于想象力的宇宙模型.

无论如何，主流物理学界倾向于甚至可以说广泛地接受大爆炸宇宙论.宇宙大爆炸已经成为人类似曾亲眼目睹或见证过的客观真实的宇宙演化史.

11.3 OR和GOR观点

似是而非是现代广义相对论的显著特征，从引力红移和引力偏折到水星近日点旋进，从引力波预测到LIGO之引力波探测，从宇宙红移到哈勃定律和宇宙膨胀学说，从黑洞理论到大爆炸宇宙论，无不体现出这一特征.这种似是而非的根源在于，爱因斯坦广义相对论，其所描述的是光学观测中呈现的自然之现象，而非自然之本质.因而，以爱因斯坦广义相对论为基础的现代广义相对论及其大爆炸宇宙论，同样显得似是而非.

观测相对论揭示了时空和物质运动的本质；基于OR和GOR理论有望解析大爆炸宇宙论之真伪.

11.3.1 大爆炸宇宙论之理论基础问题

大爆炸宇宙论，与黑洞理论一样，是现代广义相对论的产物.而现代广义相对论，包括量子引力论，则主要建立在爱因斯坦广义相对论之基础上.

然而，大爆炸宇宙学家并未认识到爱因斯坦广义相对论是一个局部理论，乃光学观测模型，仅当其观测代理OA(η)为光学观测代理OA(c)时有效.大爆炸宇宙学家并未正确地认识和理解爱因斯坦相对论，包括狭义相对论和广义相对论；并未意识到，一切相对论性，本质上，皆观测效应或表观现象.

大爆炸宇宙论中，爱因斯坦相对论之相对论性效应，诸如：时空弯曲、时间膨胀、空间伸缩、时空换位、质能变换，以及源于不确定性原理的量子能量扰动，成为其不可或缺的元素.宇宙大爆炸，从虚构的“虚时空”开始，其中，时间和空间无意义：时间是停滞的，空间是虚无的；之后，便是虚构的量子能量扰动，引发宇宙大爆炸，时空暴胀.

OR和GOR理论阐明：爱因斯坦相对论中的相对论性效应，并非客观真实的物理现实.客观真实的物理世界中，时间和空间相互独立，时间不会膨胀，空间不会伸缩，更不会弯曲；质量是守恒的，能量也是守恒的.正如BP-07所述，海森堡不确定性原理中的不确定性，本质上，也是一种观测效应，并不产生所谓的量子扰动或量子“涨落”.

既然时空不会弯曲，那么，宇宙便不会蜷缩至所谓的“引力奇点”或“大爆炸奇点”：空间不会为零，时间不会停滞.既然没有海森堡的量子“涨落”，那么，即使物质堆积在一起，无论整个的或局部的宇宙物质堆积在一起，也未必会爆炸.即使整个宇宙的物质堆积在一起，密度和温度极高，最终，大爆炸，也并不意味着诞生了一个新的宇宙或时间有了新的开始.那只是天体演化进程中某个时间点上的某次事件而已；那只是宇宙演化史的一个组成部分而已.

如此，基于爱因斯坦广义相对论的现代广义相对论和量子引力论乃至其大爆炸宇宙论，在客观真实的时空中，只能是一座空中楼阁.

归根结蒂，大爆炸宇宙论主要以爱因斯坦广义相对论为其理论基础，并且，主要引用其中的广义相对论性或引力相对论性.既然相对论性并非客观真实的物理现实，宇宙大爆炸便失去了爱因斯坦广义相对论这一理论基础，大爆炸宇宙论还能成立吗？

宇宙学家需要重新审视大爆炸宇宙论的理论基础；基于观测相对论，包括OR理论和GOR理论，重新审视爱因斯坦相对论，特别是爱因斯坦广义相对论，重建宇宙学之理论基础，重塑宇宙演化模型.

11.3.2 哈勃定律：宇宙红移与宇宙膨胀

支持大爆炸宇宙论的所谓观测证据，如宇宙红移(cosmological redshift)、宇宙微波背景辐射(cosmic microwave background)、轻元素丰度(light element abundance)、原始气体云(primordial gas clouds)，以及银河系演化和分布(galactic evolution and distribution)等，原本存在无限多种可能的解释，未必是宇宙专为大爆炸准备的证据或素材.

在大爆炸宇宙论列举的观测证据中，最重要和最直接的，自然是宇宙红移；特别地，当其被哈勃定律及其宇宙膨胀学说诠释之后，成为现代广义相对论之大爆炸宇宙论的根基和支柱.

天文观测表明，地球观测者观测到的星光光谱呈现红移现象，并且，距离地球越远的星系，其光谱红移越显著.或者说，宇宙星光之光谱红移量Z与星系随动距离D成正比；光学代理OA(c)之下，成立：

(11.1)

式中：Z为光之宇宙红移量；fe和fo分别为光之发射频率和观测频率；λe和λo分别为光之发射波长和观测波长；RED为正比系数；而D则为星星或星系之随动距离(comoving distance).

哈勃猜想，宇宙红移类似多普勒效应，乃星系相对于地球退行所致.设某星系之退行速度(resession velocity)为vr，则依Fizeau-Doppler公式，成立：

(11.2)

于是，哈勃定律[149]诞生了：

vr=H0D(vr=cZ;H0=cRED)

(11.3)

哈勃定律：根据式(11.3)，宇宙之中，所有星系相对于地球正在快速地退行，而且，距离地球越远的星系，其退行的速度越快.

哈勃膨胀学说：依据哈勃定律、哈勃推论，宇宙正在膨胀，犹如一次大爆炸后所呈现出的情景.

哈勃距离：依据哈勃定律，一定存在某个距离DH，在这个距离上，星系的退行速度vr达到光速c；因而，地球上的观测者无法观测到这些星系.

自然地，哈勃距离DH可由哈勃定律计算：

(11.4)

主流物理学界认为，哈勃定律及其宇宙膨胀学说是一个重大发现，奠定了现代宇宙学的基础，成为大爆炸宇宙论不可或缺的重要的组成部分.

然而，宇宙未必真地遵循哈勃定律.

11.3.3 光行距离与光行定律

宇宙红移并不意味着宇宙膨胀.

就光之宇宙红移而言，原本可以有各种解释.或许，受到Lemaitre之“太古原子”爆炸说(其中基于爱因斯坦广义相对论预言了宇宙膨胀)的“启发”，哈勃构思了哈勃定律及其宇宙膨胀学说.

实际上，基于GOR理论在第9章中对光之引力红移的定义和演绎，光谱红移，无论光之引力红移还是光之宇宙红移，从波的角度看，是光之频率衰减效应，此乃现象；从粒子的角度看，是光子之动能衰减效应，遵循能量守恒原理，此乃本质.

天文学家对宇宙红移的观测，属于光学观测，自然地，观测代理即光学代理OA(c) ，其中，光子动能K=hf(此即普朗克方程：E=hf).如此，基于光之动能衰减定义的宇宙红移ZED=ΔK/K与基于光之频率衰减定义的宇宙红移ZD=Δf/f等价：

(11.5)

式中：光之宇宙红移量Z=ZED代表光子动能的衰减；Ke和Ko分别为光子发射动能和观测动能.

于是，哈勃定律演化为“光行定律”：

(11.6)

式中：ZED代表光子动能的红移(衰减)；RED为光子动能红移(衰减)系数(即哈勃常数H0除以真空光速c).

光行定律：根据式(11.6)，宇宙星系辐射的光或光子在宇宙中旅行，光或光子之动能K会逐渐红移或衰减，其动能之相对红移或衰减量ZED=ΔK/K与星系随动距离D成正比，即ZED=REDD，星系与地球之随动距离D越大，其动能之相对红移或衰减量ZED越大.

光行定律的合理性是显而易见的：一粒子弹出膛之后，其动能必然会逐渐地衰减，最终，因动能耗尽而停止运动；星系辐射的光或光子，理论上，其运动与子弹的运动并无二致.宇宙并非自由时空，并非真正的“真空”；光或光子在宇宙中旅行，如同子弹在大气中飞行，同样需要消耗能量.

波，比如光波和声波，无论其在真空中或大气中或水中，总能保持其特定的速度，因而，在同一介质中，不同频率的光波或不同频率的声波，皆具有相同的速度.可以设想，波具有某种保持其特定速度的机制：当其动能衰减时，波会以降低其频率的方式维持其原有的速度；同样地，当其动能增长时，波会以提高其频率的方式保持其原有的速度.

如此，光或光子在宇宙中遨游，其动能渐渐红移或衰减；当其能量衰减到一定程度之前，依然能保持其真空光速c，继续在宇宙中运动.

然而，与一切物体或物质粒子一样，光或光子的能量会越来越低，直至无法继续通过降低频率维持其原有的速度；于是，速度逐渐下降.最终，光或光子能量耗尽，停止运动，结束其长距离的旅行.

自然地，对于光或光子，对应其有限的能量，应该存在一个有限的时间和空间为其旅行上限.我们将光或光子所能飞行的上限距离称为“光行距离”.

光行距离：依据光行定律，一定存在某个距离上限DL，超越这个距离的星系，其辐射的光或光子，由于能量的限制，无法到达地球，因而，地球上的观测者无法观测到这些星系.

光或光子之动能的相对红移(衰减)量ZED=1代表着光或光子动能Ke耗尽，此时，对应的星系随动距离D即光或光子之宇宙旅行距离之上限DL.

根据光行定律(式(11.6))：

DL=(RED)-1=
c/H0≈4.255×103Mpc(ZED=1)

(11.7)

其中，依据国际标准化组织(ISO)提供的数据进行计算，光行距离DL大约为139亿光年.

一粒子弹，其飞行距离不超过1 000 m，而飞行时间不超过2 s.一粒光子在宇宙中遨游，其飞行时间可达139亿年，而飞行距离可达139亿光年.

有趣的是，光行距离DL正是哈勃距离DH.

DL和DH有一个共同点：在这个距离上，星系辐射的光或光子，是地球上的观测者无法观测到的.

然而，特别值得注意，光行距离DL和哈勃距离DH具有完全不同的意义：光行距离DL是光子飞行距离的上限；而哈勃距离DH则以为，距离地球DH的星系，其相对于地球的退行速度vr是光速c.

根据哈勃定律和哈勃距离，D>DH时，星系退行速度岂不超越光速吗？如果是，那么，岂不有悖于爱因斯坦之“光速不变性原理”吗？

实际上，宇宙不存在所谓的“哈勃距离”DH——没有什么星系能相对于地球以光速运动；然而，光行距离DL是必须的——没有什么物质粒子可以不耗费任何能量在宇宙中永无休止地运动.

光行定律及其光行距离DL告诉我们：所谓的“宇宙膨胀”，只能是一种臆想，并非客观真实的物理现实；星系光谱之宇宙红移，并非“宇宙膨胀”效应，而是光或光子遨游宇宙之过程中，其能量损耗的表现，乃光或光子之动能的红移(衰减)效应.

光或光子在宇宙中遨游，其动能红移或衰减是必然的，不是推测；而星系退行乃至宇宙膨胀则只是一种推测，一种猜想，甚至，一种臆想.

失去了哈勃定律，失去了宇宙膨胀这一根基或支柱，大爆炸宇宙论还能成立吗？

12 伽利略- 牛顿理论与爱因斯坦理论的统一

观测相对论，包括OR理论和GOR理论，乃一般观测代理OA(η)之理论体系，概括统一了伽利略- 牛顿理论和爱因斯坦相对论.

伽利略- 牛顿理论和爱因斯坦相对论，皆观测相对论之局部理论，分属不同观测代理：伽利略理论和牛顿力学是理想代理OA∞的产物；而爱因斯坦相对论则是光学代理OA(c)的产物.OA(η)为理想代理OA∞时，观测相对论严格地约化为伽利略理论和牛顿力学；OA(η)为光学代理OA(c)时，观测相对论严格地约化为爱因斯坦相对论.

物理学局部理论的概括或部分理论的统一，不只是旧理论机械的或形式上的再现和复制，而是人类认识客观世界的进步乃至飞跃，是人类物理学理论体系之逻辑上追根溯源的一大步.将牛顿力学和爱因斯坦相对论2个伟大的理论体系统一于同一公理体系和同一理论体系，其寓意无疑是重大的.

同一物理世界，同一逻辑体系.

物理学，仅当其因果链条始于最基本的逻辑前提时，方能知其然并知其所以然，概括局部理论，将分立的理论统一起来.正如霍金[13]所言：“那时，我们就会知道上帝到底是怎么想的.”

现在，该是人类重塑其自然观的时候了.

观测相对论，包括OR理论和GOR理论，令我们认识到，伽利略- 牛顿理论乃正确理论，是客观世界之真实写照；爱因斯坦相对乃近似理论，是自然世界透过光呈现给我们的光学映像.

对话列表之表4、5乃观测相对论与爱因斯坦相对论和伽利略- 牛顿理论的类比和对话列表，归纳总结了OR理论和GOR理论以及爱因斯坦相对论和伽利略- 牛顿理论的基本关系式.类比一般观测代理OA(η)和光学代理OA(c)以及理想代理OA∞之关系式可以发现，观测相对论，既与爱因斯坦相对论具有严格的“同构一致性”对应关系，又与伽利略- 牛顿理论具有严格的“同构一致性”对应关系.

表4 OR理论与爱因斯坦狭义相对论和伽利略- 牛顿理论的对话

表5 GOR理论与爱因斯坦广义相对论和牛顿万有引力论的对话

续表5

表4显示：当η→c时，OR理论之一切关系式皆严格地约化为爱因斯坦狭义相对论之关系式；而η→∞时，OR理论之一切关系式则严格地约化为伽利略- 牛顿理论之关系式.这种不同理论体系之间严格的对应关系表明：OR理论，既与爱因斯坦狭义相对论逻辑上一致，又与伽利略- 牛顿理论逻辑上一致；同时，这种严格的对应关系印证了OR理论逻辑上的自洽性和理论上的正确性.

表5显示：当η→c时，GOR理论之一切关系式皆严格地约化为爱因斯坦广义相对论之关系式；而η→∞时，GOR理论之一切关系式则严格地约化为牛顿万有引力论之关系式.这种不同理论体系之间严格的对应关系表明：GOR理论，既与爱因斯坦广义相对论逻辑上一致，又与牛顿理万有引力论逻辑上一致；同时，这种严格的对应关系印证了GOR理论逻辑上的自洽性和理论上的正确性.

表4、5之类比和对话，有助于我们更好地理解观测相对论与爱因斯坦相对论以及伽利略- 牛顿理论之逻辑上的一致性，更好地理解观测相对论之逻辑上的合理性和自洽性，乃至其理论上的正确性，同时，有助于我们基于新的和更广阔的视角重新认识和理解爱因斯坦相对论，重新认识和理解伽利略的学说和牛顿的经典力学.

13 结束语

观测相对论，包括OR理论和GOR理论，不是为了挑战爱因斯坦相对论而“制造”的.OR和GOR理论是理论上的一次“发现”，某种意义上，是个“意外”.然而，归根结底，OR和GOR理论是逻辑的产物，是实证和思辨的产物，是科学的产物.

霍金认为：人类的物理学被分割成了许多的局部理论；而物理学的终极目标是将它们统一起来.无论伽利略- 牛顿力学还是爱因斯坦相对论，都只是霍金言下的局部理论.OR和GOR理论概括并统一了伽利略- 牛顿力学和爱因斯坦相对论，是伽利略- 牛顿力学和爱因斯坦相对论的发展.

一种新的理论，能将2种旧的理论或局部理论统一起来，其意义，想必大家是理解的.再次借用霍金[13]在其《时间简史》中所说的话：“如果我们发现一个完整的理论，那将是人类理性的终极胜利，因为，那时我们就会知道上帝到底是怎么想的.”

尽管，或者，正因为，物理学和物理学家并不十分理解光速为什么不变和时空为什么弯曲，主流物理学界视爱因斯坦相对论为圣经，容不得不同的思想和不同的见解.美国互联网电子预印本文库raXiv，其初衷是促进科学思想的自由传播，却拒绝收录OR和GOR文稿.幸好，有《北京工业大学学报》和Archive Freedom电子预印本文库viXra，OR[1,3]和GOR[16]能呈现在学术期刊和互联网上与读者见面.

OR和GOR理论未必十分严谨.然而，观测相对论之整个理论体系，包括OR理论和GOR理论，逻辑上是自洽的，既与爱因斯坦相对论逻辑上一致，又与伽利略- 牛顿理论逻辑上一致.观测相对论，既是逻辑和理论的产物，同时具有实证依据，而非臆想.笔者相信，观测相对论乃科学真理，经得起思辨，经得起实证，经得起批判，经得起时间和历史的检验.OR和GOR理论，远非终极理论，欢迎批判.然而，笔者恳请读者和物理学家，特别是主流物理学界之权威人士，为了物理学的进步和发展，少一丝不屑和苛责，多一分宽容和鼓励.如若大家能基于完善而不是扼杀观测相对论的学术态度和科学精神批判OR理论和GOR理论，笔者将倍感欣慰.观测相对论，乃一般观测代理OA(h)之理论体系，概括统一了伽利略- 牛顿理论和爱因斯坦相对论.

伽利略- 牛顿理论和爱因斯坦相对论，皆观测相对论之局部理论，分属不同观测代理：伽利略理论和牛顿力学是理想代理OA∞的产物；而爱因斯坦相对论则是光学代理OA(c) 的产物.OA(η) 为理想代理OA∞时，观测相对论严格地约化为伽利略理论和牛顿力学；OA(η) 为光学代理时OA(c) 时，观测相对论严格地约化为爱因斯坦相对论.

同一物理世界，同一逻辑体系.

现在，该是人类重塑其自然观的时候了.

致谢

特别感谢《北京工业大学学报》编辑部及其全体工作人员，特别感谢《北京工业大学学报》宋国恺主任、吕小红执行主编、严辉副主编为发表GOR理论所做出的努力；特别感谢严辉教授、蒋毅坚教授、阮平南教授、翟天瑞教授、宋国恺教授参与对本文形式和内容的审核；最后，特别感谢Archive Freedom电子预印本文库viXra收录OR和GOR文稿.

广义观测相对论：时空在爱因斯坦广义相对论中为什么弯曲？(下篇)——GOR理论与科学预言

7 GOR理论与行星轨道之旋进

7.1 天体运行图像的演化

7.2 牛顿之行星运动方程

7.3 爱因斯坦之行星运动方程

7.4 GOR行星运动方程

7.5 GOR理论与行星轨道的旋进

7.6 天体运行论的统一

8 GOR理论与光之引力偏折

8.1 关于光之引力偏折

8.2 牛顿万有引力论与光之引力偏折

8.3 爱因斯坦广义相对论与光之引力偏折

8.4 GOR理论与光之引力偏折

8.5 光之引力偏折：现象与本质

9 GOR理论与光之引力红移

9.1 关于光之引力红移

9.2 爱因斯坦广义相对论与光之引力红移

9.3 牛顿万有引力论与光之引力红移

9.4 GOR理论与光之引力红移

10 GOR理论与引力波

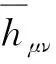
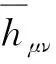
10.1 爱因斯坦之波方程：引力波预言

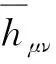
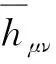
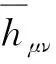
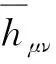
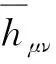
10.2 引力波探测：LIGO工程

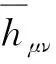
10.3 GOR理论之波方程：信息波方程

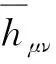
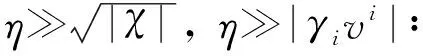
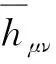
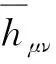
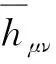
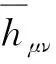
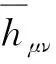
10.4 重新诠释LIGO之引力波

11 GOR理论与宇宙大爆炸

11.1 问题陈述

11.2 主流学术界的观点

11.3 OR和GOR观点

12 伽利略- 牛顿理论与爱因斯坦理论的统一

13 结束语

广义观测相对论：时空在爱因斯坦广义相对论中为什么弯曲？(下篇)
——GOR理论与科学预言