基于振幅加权的拖缆与海底地震资料联合波形反演方法

杨华臣， 张建中,2*， 吴志强

1 海底科学与探测技术教育部重点实验室， 中国海洋大学海洋地球科学学院， 青岛 266100 2 青岛海洋科学与技术国家实验室， 海洋矿产资源评价与探测技术功能实验室， 青岛 266237 3 自然资源部海洋环境地质重点实验室， 青岛海洋地质研究所， 青岛 266071

0 引言

南黄海位于中国大陆和朝鲜半岛之间，是我国近海唯一没有实现油气突破的盆地(吴志强等，2019).一个主要原因是新近系沉积层直接覆盖在中-古生代海相地层之上(张海啟等，2009)，形成了反射系数高达0.5的强反射界面(吴志强等，2015；赵维娜等，2019)，严重阻碍了地震波向下传播和深部反射波向上传播.而且，海相碳酸盐岩地层之间的速度和密度差异小，难以形成能量较强的反射波(吴志强，2009；杨艳秋等，2015；Zhang et al.，2019).这些因素导致南黄海地震资料的中深部地层反射波能量极弱，加大了该地区中深部海相地层地震勘探的难度.

全波形反演方法充分利用地震波的运动学和动力学信息反演地下介质的速度(蒋梦凡等，2021；尚旭佳等，2021)，是目前速度建模精度和分辨率最高的方法之一(Virieux and Operto，2009)，在常规的海洋拖缆地震勘探中已经取得了很多成功的应用案例(Warner et al.，2013；Wang et al.，2016，2021).然而，由于拖缆水听器性能的限制，拖缆地震资料缺乏低频信号(Hondori et al.，2015)，当初始速度模型严重偏离真实模型时，全波形反演方法往往收敛于局部极小值，导致反演失败(Virieux and Operto，2009).海底地震资料(OBN/OBS)含有丰富的低频地震信号，利用这些低频成分，全波形反演方法可以构建低波数背景速度场，降低了对初始速度模型精度的要求(Kamei and Pratt，2010；Plessix et al.，2013).但是，OBN/OBS的空间分布远比拖缆中的水听器稀疏，限制了全波形反演速度模型的分辨率.

拖缆与海底地震资料在频率成分和空间采样密度上具有优势互补性.联合使用这两种资料，可以充分发挥海底地震资料低频成分丰富而拖缆中水听器空间分布密集的优势，提高全波形反演的效果.因此，我们提出了拖缆与OBS资料联合全波形反演方法(Yang and Zhang，2019)，利用Marmousi2模型的合成资料，验证了该方法的优越性.但是，该方法没有考虑不同界面反射波振幅的差异.特别是对于南黄海地震资料，该方法能正确反演浅部沉积层的速度，而对中深部海相地层的反演效果较差.

在提高深部地层速度反演效果方面，Zhang等(2012)使用反传波场的能量对全波形反演目标函数的梯度进行加权处理.当初始速度模型较为光滑时，计算的加权能量不够准确，降低了目标函数的收敛速度.为此，张凯等(2015)使用反射波地震资料利用反偏移方法计算加权能量并对梯度进行加权处理.管建博等(2021)采用拟Hessian算子对梯度进行加权处理，从而增强模型深部的照明.上述方法在一定程度上改善了对深部地层的反演效果.但是，当深部地层展布复杂，地震覆盖次数少、照明强度较弱时，该类方法难以正确补偿深部地层的梯度，从而降低反演收敛速度，甚至使得反演收敛于局部极值.而且，反偏移和拟Hessian算子的计算量较大.

在我们的拖缆与OBS资料联合全波形反演方法(Yang and Zhang，2019)的基础上，本文提出了一种基于振幅加权的拖缆与海底地震资料联合波形反演方法.该方法利用反射波振幅的方差进行加权处理，平衡波形反演中不同深度地层的反射波强度，改善了反演的整个速度模型，尤其是对深部地层的效果得到极大提高.此外，联合使用拖缆和海底地震资料进行全波形反演，克服了一种资料的缺陷，实现这两种资料的优势互补.基于南黄海地震和钻井资料(吴志强等，2012，2014，2019)，建立了南黄海中部隆起的一条速度模型剖面.然后，用该模型的合成地震记录对本文方法进行了测试和分析.

1 方法原理

1.1 目标函数

我们原提出的拖缆与OBS资料联合全波形反演的目标函数为(Yang and Zhang，2019)：

(1)

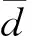
(2)

其中，n表示积分次数，τ表示积分区间，c1和c2分别表示第s炮r道地震记录积分前、后的最大值，它们的作用是使积分前后地震记录振幅的量级一致.

式(1)所示的目标函数使用了三种地震资料，分别是拖缆地震资料、OBS资料和积分后的拖缆地震资料.对拖缆地震资料进行积分可以获得其包含的低频成分，补充稀疏OBS资料低频成分的照明不足.OBS资料和积分后的拖缆地震资料含有丰富的低频数据.在反演初期，利用这些低频地震数据可以有效地构建反演速度模型的背景场.在反演后期，充分利用拖缆地震资料的高频成分，可以逐步提高反演速度模型的分辨率和精度.

在式(1)所示的目标函数中，权重系数仅与地震资料的种类有关，而与反射波振幅无关.当不同双程走时的反射波振幅差异极大时，该目标函数主要体现了对强振幅反射波的拟合情况.对于南黄海地震记录，浅部沉积层和新近系与中-古生代海相地层间界面的反射波振幅大，而其下方中-古生代海相地层对应的反射波振幅非常小.采用该目标函数，可以正确反演浅部沉积层的速度，而难以有效反演深部中-古生代地层的速度.

为了提高对强反射界面之下中-古生代地层速度的反演效果，增加深部地层反射波数据在全波形反演目标函数中的权重，本文提出一种新的目标函数：

(3)

其中，w1、w2和w3分别表示拖缆地震记录、OBN记录和积分后的拖缆地震记录对应的振幅加权系数.根据第1次迭代得到的地震记录残差，计算这三个振幅加权系数，表达式为：

(4)

其中，Δd表示第1次迭代模型计算的与观测的地震记录之间的残差，σ表示地震记录残差Δd的标准差，ε表示阻尼系数，用于防止σ接近0时不稳定现象的发生.标准差σ采用式(5)计算：

(5)

其中，wt表示进行方差估计的时窗长度，M表示时窗内地震记录残差Δd的均值.

相比于式(1)，式(3)增加了3个振幅加权系数.该系数仅与第1次迭代的地震记录残差有关，而与反演速度模型无关.故可以将该系数视为与反演速度模型无关的独立变量.因此，式(3)和式(1)所示目标函数的最小化方法类似，仅需要利用式(4)对地震记录残差额外进行振幅加权.相比于正演模拟，振幅加权需要的计算时间可以忽略不计.

1.2 最优化反演

采用共轭梯度法求取式(3)所示目标函数的极小解(Scales，1987；Hu et al.，2011).当前迭代的共轭梯度可以表示为当前迭代的梯度和前一次迭代的共轭梯度的线性组合(Mora，1987；Tarantola，1987)：

(6)

(7)

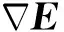
求得共轭梯度，即搜索方向后，采用式(8)对当前迭代的速度模型进行更新：

vk+1(x)=vk(x)+λkdk(x)，

(8)

其中，vk+1表示更新后的速度，λk表示迭代更新的步长.步长采用线性搜索方法进行计算(Hager and Zhang，2005).

1.3 梯度计算

式(3)所示目标函数对速度的梯度可以表示为：

(9)

其中，g1、g2和g3分别表示目标函数中各项对速度的梯度.α1、α2和α3分别表示g1、g2和g3对应的权重，与原方法中权重的计算方法相同(Yang and Zhang，2019)，用于实现对三种地震资料对应梯度进行归一化处理，从而消除三种地震资料间量纲和覆盖次数等差异对反演的影响.式(9)表明当拖缆资料缺乏低频数据时，可以通过OBN资料和积分后拖缆地震记录的低频数据对低波数背景速度场进行反演.在反演迭代后期，可以通过拖缆资料的高频成分反演模型的高波数细节信息.因此，联合使用拖缆和OBN资料可以实现两者优势互补.

式(9)中梯度的具体计算公式为(Yang and Zhang，2019)：

(10)

(11)

(12)

其中，ωr和ωo分别表示拖缆和OBN资料的角频率，pf(x，ωr)和pf(x，ωo)分别表示拖缆和OBN资料频率域震源正传波场，pb(x，ωr)和pb(x，ωo)分别表示拖缆和OBN资料频率域检波点反传波场，pf(x，t)和pb(x，t)分别表示积分后拖缆地震记录时间域震源正传波场和检波点反传波场，符号Re表示取复数的实部，上标*表示复数的共轭.频率域地震波场通过对时间域地震波场进行傅里叶变换得到(Xu and McMechan，2014；Yang and Zhang，2019).

不同于无振幅加权波形反演方法(式(1))，本文方法在计算检波点反传波场时使用的不是预测的和观测的地震记录的残差或其积分，而是进行振幅加权后的地震记录残差或其积分.其中，拖缆资料、OBN资料和积分后拖缆资料对应的反传震源分别为：

sb(s,r,t)=w1(s,r,t)[dcal(s,r,t)-dobs(s,r,t)]，

(13)

sb(s,o,t)=w2(s,o,t)[dcal(s,o,t)-dobs(s,o,t)]，

(14)

(15)

1.4 波场计算

本文采用下列常密度声波方程合成式(1)、(3)中的预测地震记录(梁文全等，2013)：

(16)

其中，v表示地震波在地下介质中的传播速度，x表示空间坐标，xs表示震源的空间坐标，t表示时间，pf表示震源正传波场，sf表示震源函数.

2 模型测试与分析

2.1 资料合成

根据南黄海中部隆起地震剖面解释结果和地层物性资料(吴志强和陆凯，2011；吴志强等，2014)，建立了如图1a所示的理论速度模型(模型两侧覆盖次数较少，故仅显示了用于与反演结果对比的模型中间部分).模型大小为25 km×6.25 km.模型顶部为海水层，其厚度为50 m，速度为1.5 km·s-1.海水层下方是厚度约为600 m的第四系和新近系沉积层，其速度从顶部的1.55 km·s-1随深度增加到2.2 km·s-1.新近系沉积层下方是中-古生代海相地层，速度介于3.7～6.2 km·s-1，平均速度约为5 km·s-1.相比于第四系和新近系沉积层，中-古生代海相地层的速度结构复杂，在横向与纵向上变化较大.值得注意的是，新近系沉积层与其下方的中-古生代海相地层之间速度差异很大，在深度约为650 m处存在明显的强速度差界面，该界面的反射系数可达0.5左右.

图1 速度模型(a) 理论速度模型，圆点和三角形分别代表图3中第52炮炮点和第40个OBN的位置； (b) 初始速度模型； (c) 拖缆资料无振幅加权波形反演模型； (d) OBN资料无振幅加权波形反演模型； (e) 拖缆资料有振幅加权波形反演模型； (f) OBN资料有振幅加权波形反演模型.Fig.1 Velocity models(a) Theoretical velocity model；The dot and triangle indicate the locations of the 52th shot and 40th OBN as shown in Fig.3, respectively; (b) Starting velocity model for FWI tests； (c) Velocity model inverted by FWI of the towed-streamer seismic data without amplitude weighting； (d) Velocity model inverted by FWI of the OBN data without amplitude weighting； (e) Velocity model inverted by FWI of the towed-streamer seismic data with amplitude weighting； (f) Velocity model inverted by FWI of the OBN data with amplitude weighting.

在合成拖缆多道地震资料时，将拖缆的排列长度设置为7.5 km，道间距25 m，共300道.拖缆位于震源后方，并随着震源同步移动.拖缆中的水听器与震源之间的最小偏移距为25 m，最大偏移距为7.5 km.在合成OBN资料时，将63个OBN以400 m的间距均匀布设在海底(Z=50 m).震源以200 m的间距从模型左侧X=7.5 km处开始激发直到模型的最右侧.拖缆中的所有水听器和OBN均同时记录地震波场.

采用边长25 m的正方形网格离散速度模型、2 ms的时间采样率和4 s的时间采样长度.使用时间二阶、空间十二阶精度的有限差分方法模拟地震波场(Alford et al.，1974；Liu and Sen，2009).采用PML边界条件压制模型边界处的反射波场(王维红等，2013).采用主频为10 Hz的雷克子波作为震源.

为了模拟实际观测拖缆地震记录中缺乏低频成分的特点，对合成的拖缆地震记录进行5 Hz的高通滤波.高通滤波器如图2a所示.图3a是5 Hz高通滤波后震源位于海面X=17.7 km处(图1a中圆点所示位置)的拖缆资料第52炮共炮集记录.可以看出，在1～2 s的时间范围内存在一个强能量的反射波同相轴.该同相轴即为新近系沉积层与中-古生代海相地层间强反射界面的反射波同相轴.在该强反射波同相轴下方，仅能识别出个别振幅较弱的同相轴.这表明新近系和中-古生代地层间的强速度差界面严重阻碍了地震波的向下传播，导致强速度差界面之下地层的反射波能量微弱.

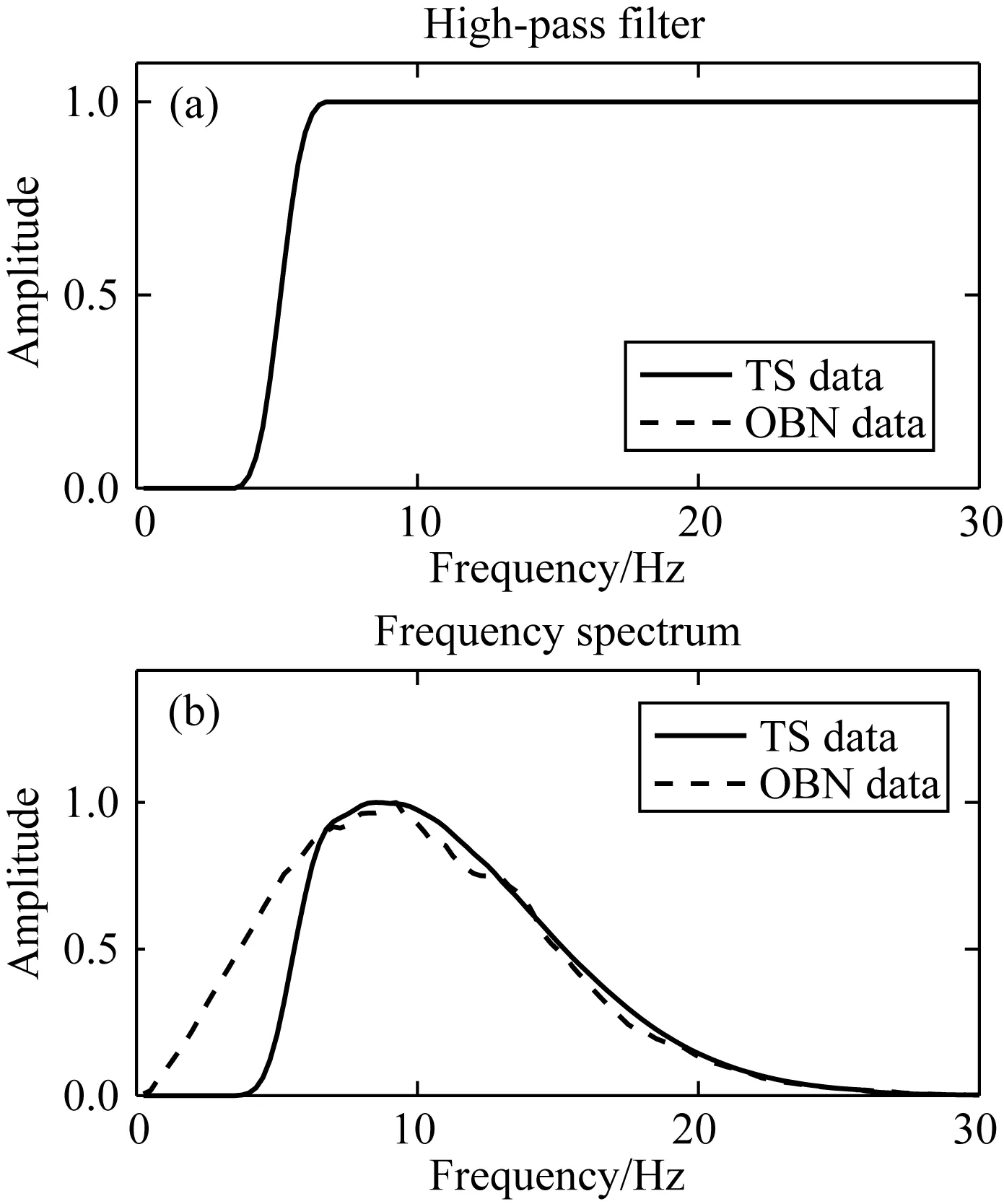
图2 高通滤波器(a)与合成地震记录频谱(b)(b)中实线和虚线分别表示拖缆和OBN记录的频谱.Fig.2 High-pass filter (a) and frequency spectrum of synthetic seismic data (b) Solid and dashed lines in (b) indicate the frequency spectrum of Towed-Streamer (TS) and OBN data, respectively.

图3e是震源位于海底15.625 km处(图1a中三角形所示位置)的第40个OBN共接收点道集记录.与拖缆合成地震记录类似(图3a)，在1～2 s的时间范围内存在能量较强的反射波同相轴，而其余时间范围内的反射波同相轴能量弱.不同的是，拖缆地震记录缺乏低频成分而OBN记录中含有丰富的低频成分，如图2b所示.

图3 地震记录(a)—(d) 拖缆资料第52炮共炮域地震记录(震源位于图1a中圆点处)； (e)—(h) 第40个OBN共接收点域地震记录(OBN位于图1a中三角形处)； (a)和(e) 合成地震记录； (b)和(f) 第1次迭代初始模型的合成地震记录； (c)和(g) 第1次迭代无振幅加权时的地震记录残差； (d)和(h) 第1次迭代有振幅加权的地震记录残差，wt=1 s，ε=0.01.Fig.3 Seismic data(a)—(d) Towed-streamer seismic data of the 52nd common shot gather with the shot located at the dot in Fig.1 a； (e)—(h) OBN data of the 40th common receiver gather with the receiver located at the triangle in Fig.1 a； (a) and (e) Synthetic seismic data；(b) and (f) Predicted seismic data after the first iteration； (c) and (g) Difference between the synthetic and predicted seismic data without amplitude weighting； (d) and (h) Difference between the synthetic and predicted seismic data with amplitude weighting using a 1 s weighting window and a damping factor of 0.01.

为了更清楚地显示新近系沉积层与中-古生代海相地层间强反射界面对地震波能量的屏蔽作用，采用合成的拖缆资料进行逆时偏移成像，获得的逆时偏移成像剖面如图4所示，逆时偏移采用图5c所示与理论模型非常接近的速度模型.可以看出，在深度约为650 m处的同相轴振幅非常大，而其下方同相轴振幅非常小，体现了强反射界面对地震波的阻滞作用.

图4 拖缆资料逆时偏移成像剖面Fig.4 Reverse time migration images of the towed-streamer seismic data

2.2 单一资料反演

先用无振幅加权的全波形反演方法分别对合成的拖缆和OBN资料进行了反演.图1b是理论速度模型平滑后的结果，将其作为全波形反演的初始速度模型.对于拖缆资料，使用4个较高的频率成分进行反演，频率分别是6 Hz、7.2 Hz、8.64 Hz和10.37 Hz.每个频率成分均迭代15次，共迭代60次.图1c是反演速度模型.对比图1b、c可以看出，大约650 m深度以上的沉积层速度得到了较好地反演，而在该深度以下，反演速度与理论速度值(图1a)相差较远.

对于OBN资料，采用2 Hz、2.8 Hz、3.92 Hz和5.49 Hz这4个频率较低的成分进行反演，同样地，每个频率成分迭代15次.图1d是反演速度模型.可以看出，模型浅部沉积层的速度(Z<650 m)得到了较好地反演，与理论速度值(图1a)非常接近.中深部中-古生代地层的反演结果(Z>650 m)远远优于拖缆资料的反演结果(图1c).这主要是由于OBN资料含有更容易穿透强反射界面的低频成分，低频地震成分更有利于确定速度模型的低波数变化.然而，整体上，OBN资料反演速度模型与理论模型的差异仍然较大.

为了测试地震记录振幅加权对全波形反演速度模型的影响，用有振幅加权的波形反演方法分别对合成的拖缆和OBN资料进行了反演.式(4)中的阻尼系数ε设置为0.01，式(5)中的振幅加权时窗wt设置为1 s.图3b、f分别是用第1次迭代初始模型预测的拖缆地震资料第52炮共炮集记录和第40个OBN共接收点集记录.图3c、g分别是无振幅加权时第1次迭代预测的与合成的拖缆与OBN记录的残差.图3d、h分别是有振幅加权时第1次迭代预测的与合成的拖缆与OBN记录的残差.可以看出，在未进行振幅加权时，1～2 s范围内的同相轴的振幅非常大，而其余范围内同相轴的振幅非常小.进行振幅加权后，浅、中和深部反射波同相轴的振幅相当，中深部反射波同相轴得到了明显地增强.

图1e、f是用振幅加权波形反演方法分别对拖缆和OBN资料的反演速度模型.可以看出，对地震记录进行振幅加权可以使中深部地层速度的反演效果得到较大提高，但与理论模型仍有较大差距，尤其是仅使用拖缆地震资料时.上述测试结果表明，对于类似南黄海的地层速度结构，仅使用单一的拖缆资料或OBN资料难以获得令人满意的波形反演结果.

2.3 拖缆与OBN资料联合反演

2.3.1 振幅加权对反演模型的影响

采用有无振幅加权波形反演方法分别对合成的拖缆和OBN资料进行联合反演.使用的拖缆和OBN资料的频率成分与2.2节单一资料反演的相同.反演分为4个频率段，每段分别使用拖缆和OBN资料的一个频率成分.同时，每段的积分时窗(式(2)中的τ)分别设置为20 ms、16 ms、12 ms和8 ms，积分次数(式(2)中的n)均设置为200.每段迭代15次，共迭代60次.

图5a是无振幅加权波形反演方法联合使用拖缆地震资料、OBN资料和积分后的拖缆地震资料的反演速度模型.相比于使用拖缆或OBN资料的反演速度模型(图1c、d)，联合反演速度模型更接近理论速度模型，但中深部地层的反演速度与理论值仍然相差较远.

图5 反演速度模型(a) 无振幅加权波形反演方法反演速度模型； (b)—(d) 本文方法wt=1 s，ε分别为0.1、0.01和0.00001时的反演速度模型.Fig.5 Inverted velocity models(a) Velocity model obtained using the FWI without amplitude weighting； (b)—(d) Velocity models obtained using the proposed FWI with a 1 s weighting window and damping factors of 0.1, 0.01 and 0.00001, respectively.

采用本文的有振幅加权波形反演方法时，将阻尼系数(式(4)中的ε)设置为0.1，振幅加权时窗(式(5)中的wt)设置为1 s.图5b是迭代60次后的反演速度模型.与无振幅加权波形反演模型(图5a)相比，该模型更接近理论速度模型，尤其是中深部地层.图6b、c分别是有无振幅加权波形反演速度模型的相对误差.相比于初始速度模型的相对误差(图6a)，无振幅加权波形反演模型的浅部地层(Z<650 m)的相对误差明显较小，而深部地层的相对误差仍然较大；有振幅加权波形反演的浅部和深度地层的相对误差均较小.这表明有振幅加权波形反演方法对南黄海地震地质模型具有更好地反演效果.

图6 速度模型的相对误差(a) 初始速度模型； (b) 无振幅加权波形反演方法反演速度模型； (c)—(d) 本文方法wt=1 s，ε分别为0.01和0.00001时反演速度模型.Fig.6 Relative errors of velocity models(a) Starting model； (b) Velocity model obtained using the FWI without amplitude weighting； (c)—(d) Velocity models obtained using the proposed method with a 1 s weighting window and damping factors of 0.01 and 0.00001, respectively.

图7a、b分别是无、有振幅加权波形反演在第1次迭代的梯度.可以看出，后者在整个模型空间均存在较大的梯度值，而前者在浅部梯度值较大，而在中深部的梯度值非常小.这说明有振幅加权的方法计算的梯度更有利于对深部地层的修正，进一步反映了有振幅加权方法的优势.

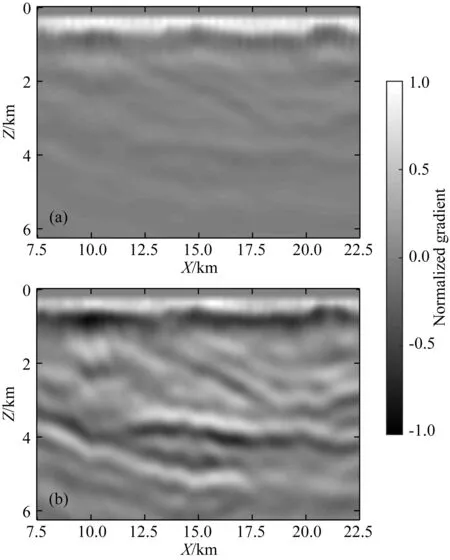
图7 第1次迭代的梯度(a) 无振幅加权波形反演方法； (b) 本文方法.Fig.7 Velocity gradients of the first iteration(a) FWI without amplitude weighting； (b) The proposed method.

2.3.2 阻尼系数对反演模型的影响

图5b、c、d是振幅加权时窗为1 s、阻尼系数分别为0.1、0.01和0.00001时本文方法的反演模型.可以看出，振幅加权时窗相同时，随着阻尼系数的减小，反演模型中的噪声逐渐变得严重，如图6所示.这主要是由于阻尼系数过小时，正演模拟数值扰动增强，从而在反演过程中引入噪声，降低反演模型质量.图8中细实线、虚线、粗实线和点线分别表示无振幅加权波形反演方法和阻尼系数分别为0.1、0.01和0.00001时本文方法反演速度模型的均方根误差随迭代次数的变化曲线.可以看出，对于不同的阻尼系数，本文方法反演速度模型的均方根误差均小于无振幅加权波形反演方法的反演结果.当阻尼系数为0.01时，本文方法反演速度模型的均方根误差最小.这表明阻尼系数与正演模拟数值扰动的量级相当时本文方法反演效果最好，而过大或者过小的阻尼系数都不利于获得最佳的反演速度模型.光滑初始模型模拟记录中直达波后的波形即为数值扰动波形，其最大振幅反映了数值扰动的量级.

图8 反演速度模型均方根误差随迭代次数的变化曲线Fig.8 RMSE curves of inverted velocity models

2.3.3 时窗长度对反演模型的影响

为了测试振幅加权时窗wt对本文方法反演速度模型的影响，将阻尼系数ε设置为0.01，时窗长度分别设置为0.1 s、0.2 s和0.5 s.0.1 s等于地震资料的主周期(主频的倒数).采用与2.2节相同的频率成分、积分次数、积分时窗和迭代次数等参数，反演速度模型分别如图9a—c所示.图9a所示速度模型与理论模型相差较远，尤其是中深部地层.这表明振幅加权时窗为地震记录的主频周期(主频的倒数)时，采用过小的时窗进行振幅加权会严重破坏反射波波形，难以获得正确的反演结果.当振幅加权时窗为0.2 s和0.5 s，大于或等于主频周期的2倍及以上时，反演模型相差较小，均非常接近理论速度模型.

图9 本文方法反演速度模型(a)—(c) ε=0.01，wt分别为0.1 s、0.2 s和0.5 s时的反演速度模型.Fig.9 Velocity models obtained using the proposed method(a)—(c) ε is 0.01 and wt is 0.1 s, 0.2 s and 0.5 s, respectively.

图10是上述3个试验反演速度模型的均方根误差随迭代次数的变化曲线.实线表示振幅加权时窗为0.1 s时反演模型的均方根误差，其余曲线表示另外2个试验反演速度模型的均方根误差.可以看出，当振幅加权时窗过小时，反演模型的均方根误差非常大.当振幅加权时窗长度为0.2 s和0.5 s时，不同试验反演速度模型的均方根误差均非常接近，且随着迭代次数的增加而逐渐下降.这表明当振幅加权时窗大于或等于两倍主频周期时，本文方法具有较好的稳定性，且能获得高精度的速度模型.

图10 反演速度模型的均方根误差Fig.10 RMSE curves of inverted velocity models

3 结论

南黄海特殊的地质结构，使在观测面接收的中-古生代海相地层的反射波能量极弱.这些弱反射波数据在一般全波形反演目标函数中的比重较小，难以获得满意的中-古生代海相地层速度模型.本文提出了一种新的拖缆与海底地震资料联合全波形反演方法.该方法通过对地震记录进行振幅加权，从而提高中-古生代海相地层反射波在目标函数中的权重，实现对自浅至深所有地层速度的有效反演.理论模型试验表明，该方法充分发挥了拖缆资料、拖缆资料积分和海底地震资料的优势互补作用，显著提高了中深部的中-古生代海相地层速度反演精度，是南黄海中深部速度建模的有效方法.

振幅加权时窗和阻尼系数是地震记录振幅加权的两个重要参数.振幅加权时窗应介于两倍至五倍地震记录主频周期之间，这时反演模型精度高，且受振幅加权时窗变化的影响较小.阻尼系数的大小应与光滑模型正演模拟数值扰动的最大振幅相当，取得过大或过小都会影响反演模型的精度.

由于缺乏南黄海同一测线的拖缆和OBN实际资料，本文仅使用理论模型合成资料进行实验和分析.对于实测资料还存在多次波和噪声等问题，需要进一步研究.