基于GNSS的再分析资料对流层延迟精度评估

上官明， 程旭， 潘雄， 党萌， 吴露振， 谢自春

1 中国地质大学(武汉)地球物理与空间信息学院，地球内部多尺度成像湖北省重点实验室， 武汉 430074 2 中国地质大学(武汉)地理与信息工程学院， 武汉 430078 3 武汉纺织大学计算机与人工智能学院, 武汉 430200

0 引言

对流层延迟(ZTD)指卫星的电磁波信号在传播过程中穿过中性大气层(50 km以下未被电离部分)所产生的信号延迟，其延迟量从天顶方向到低仰角方向在2～20 m左右，对定位精度影响较大，在利用全球导航卫星系统(GNSS, Global Navigation Satellite System)进行定位过程中，对流层延迟是主要的误差源之一.而由于信号传播路径上的气象参数难以确定，一般通过天顶方向延迟结合映射函数对信号路径上的延迟进行计算.因此，很多学者针对天顶对流层延迟建立模型并对模型精度进行了相应研究.Hopfield(1969)及Saastamoinen(1972)提出的Hopfield和Saastamoinen(SAAS)模型为目前常用的气象数据经验模型，且SAAS因较高的精度常被用于计算ZTD.除此之外还有基于气象数据的经验模型如GPT2w、UNB3m模型(Leandro et al.,2006; Böhm et al.,2015),以及全球对流层延迟经验模型GZTD(姚宜斌等，2013)、GZTD-6h(姚宜斌等，2015)，使用了基于ECMWF再分析资料建立的GGOS Atmosphere资料，该模型相对传统模型精度有了一定提高，ITG(Yao et al.,2015)利用了ERA-Interim建立了对流层延迟格网模型，相比于利用NCAR资料取得一定优化，GGZTD(黄良珂等，2021)利用MERRA2分析了纬度与ZTD的关系，并建立了高精度的ZTD滑动窗口模型，GridZWD(Yao et al.,2018)使用ERA-Interim建立了高精度的全球ZWD格网模型,相对传统的GPT2w、SAAS等模型都有了提升，但因顾及全球性，在某些特定区域的精度优势不明显.Ding等(2016)、 Ding和Hu(2019) 提出了利用神经网络建立基于SAAS的俄罗斯区域ZTD模型，该模型在俄罗斯区域内比传统SAAS模型精度提升12.4%.马下平等(2020)以探空站为基准分析了SAAS、GZTD、UBN3m、GPT2w四种模型，得出该四种模型中GPT2w的精度最优.王群等(2021)通过ERA5和探空数据建立了江苏区域的加权平均温度模型，以探空为真值时双因子模型相比利用探空数据建立的模型精度最大提高10.52%，验证了ERA5及探空在江苏区域建立加权温度模型的可行性.Chen和Liu(2016) 系统分析了大多数的对流层干湿延迟模型，比较了18种ZHD模型和9种ZWD模型精度，得出ZHD模型精度最大可达毫米级，其中ECMWF的ZHD模型与中国地区探空资料吻合度最好，但ZWD模型精度只能达到厘米级.丁茂华(2020)比较了常见的几种湿延迟模型并利用神经网络建立了ZWD模型和加权平均温度模型，相比传统的SAAS等模型精度有了提升，但由于神经网络模型的建立机制相对复杂，训练过程繁琐，使用不便.而再分析资料含有多种气象参数，为对流层的研究提供了极大便利，在这些模型的建立与评估过程中，再分析资料经常被用到，且其用途远不止于此.

尤其是在无实测气象数据的测站，无法直接计算PWV等重要参数时，可利用再分析数据进行测站处的气象参数获取，并最终得到PWV.如Zhang等(2019a，b)发现ERA5的参数相对ERA-Interim反演PWV的潜力很大，由ERA5气象参数直接计算得到的PWV与真值非常接近，都在4 mm以内甚至更高.王帅民(2021)利用ERA5建立了全球对流层延迟及PWV的模型，与真值均方根误差也在4 mm以内.赵静旸等(2014)评估了ERA-Interim在中国区域计算PWV的精度，得出其结果与实测数据接近.王群(2020)基于ERA5数据所建的加权平均温度模型进行PWV解算，结果有了一定提升.周李丹和张红星(2018)利用再分析资料提供的高精度水汽参数提出了一种新的划分垂直方向层析网格的方法，相比传统方法精度提升了12%和17%.常亮和何秀凤(2010)结合再分析资料针对附近无气象传感器GPS站点进行了PWV估计，得出较高精度的PWV，后续可用于降雨预报.

再分析资料与PPP的融合技术也在逐渐发展.精密单点定位技术(precise point positioning，PPP)是在RTK技术发展之后兴起的.相比相对定位的方式，其具有灵活性高、成本低，工作方式简单等各种优势.PPP主要是利用载波相位观测值以及高精度的轨道和钟差等产品解算出高精度的位置，需要一定时间才能收敛得到固定解(刘经南和叶世榕，2002)，其定位精度随着轨道产品钟差产品的提高而在不断提升，在很多行业如精密授时、海洋测绘等都有着越来越多的应用(Zumberge et al.，1997; 张小红等，2006).张朝怡等(2021)对ERA-Interim应用于定位中的效果作了分析并得出加入ERA-Interim后三个方向定位结果都得到提升，尤其在U方向提升近0.5 m.

可见，再分析资料在对流层建模、导航定位及气象中的应用非常广泛，其包含风速、地表温度、蒸发量、可降水量等多种参数，随着可同化的数据越来越多以及同化方法的改进，精度和分辨率也越来越高，进一步拓展了运用领域.再分析资料的精度一定程度上影响了其适用性，因此有必要对其精度进行分析.已有多名学者分析了欧洲中期天气预报中心(ECMWF)的ERA5、ERA-Interim计算对流层延迟的精度(徐康等，2020；张永林和蔡昌盛，2020).但目前针对中国2021年发布的CRA40及美国NASA在2015年发布的最新一代再分析产品MERRA2的评估相对较少，或者只针对某些区域进行了评估，且没有对其应用在精密单点定位的精度进行验证.谢劭峰等(2021)比较了ERA5、MERRA2计算的加权平均温度在中国区域的精度，刘梦杰等(2021)分析了CRA40和ERA5的气压、气温、加权平均温度及ZTD等参数在中国区域的适用性，得出CRA40计算的温度和加权平均温度相对ERA5较好，但气压及计算的ZTD精度相对ERA5较差.

本文选取了全球125个IGS站和180个探空站，利用三种再分析产品(ERA5、 MERRA2、CRA40)计算站点处的天顶对流层延迟(ZTD、 ZWD、 ZHD)，进行了精度评估，并分析其在精密单点定位中的适用性.所得的结果可为导航定位提供便利，为ZTD等气象参数建模所需数据的选取提供参考，服务于大气降水等天气变化的研究.

1 对流层延迟计算

1.1 数据来源

(1) ERA5

第五代再分析资料ERA5由欧洲中尺度预报中心(ECMWF, the European Center for Medium-Range Weather Forecasts)发布(https:∥cds.climate.copernicus.eu/cdsapp#!/search?text=ERA5&type=dataset,最近访问时间：2022.3.20)，其时间分辨率相对ERA-Interim有了很大提升.本实验选取的是空间分辨率为0.25°×0.25°的逐小时、气压层为37层的产品，参数选取温度、比湿度和位势高，从地面到1 hPa.

(2) CRA40

中国气象局2021年发布的我国第一代大气再分析资料产品CRA40(http:∥www.nmic.cn/dataService/cdcindex/datacode/NAFP_CRA40_FTM_6HOR/show_value/normal.html,最近访问时间：2022.3.20 )，本实验选取空间分辨率为0.5°×0.5°时间分辨率为6 h的产品进行分析.参数选取同ERA5，但其比湿度只覆盖了1000～100 hPa.

(3) MERRA2

MERRA2是由NASA发布的再分析资料(https:∥disc.gsfc.nasa.gov/datasets/M2I6NPANA_5.12.4/summary?keywords=MERRA2, 最近访问时间：2022.3.20)，其气压层数据达到42层，从0.1～1000 hPa，本实验选取的产品空间分辨率为0.625°×0.5°，时间分辨率为6 h，参数选取同ERA5.

针对MERRA2的近地表的气压层的湿度、温度参数缺失和CRA40的比湿度在100 hPa以上高度数据缺失的问题，本文使用GPT2w对其进行补偿.

(4)探空站和IGS站

本文选取的探空站点数据来源于怀俄明网站(http:∥weather.uwyo.edu/upperair/sounding. html, 最近访问时间：2022.3.20).该数据以文本形式提供，用户可通过代码进行下载使用.其参数包含了湿度、温度、位势高、气压以及可降水量等，相对齐全.其站点全球覆盖，从1973年开始陆续建立.本文在所有站点选取了含2020年数据且缺失天数较少的(缺失天数在6天以内).IGS选取原则也是如此，参考值采用IGS提供5 min的ZTD产品，其精度可达4 mm(Byun and Bar-Sever,2009)，数据通过CDDIS网站下载(https:∥cddis.nasa.gov/archive/gnss/products/troposphere/zpd/2020/,最近访问时间：2022.3.20).

1.2 ZTD计算方法

通常用于计算ZTD的模型有SAAS模型和积分模型，积分的精度高于SAAS模型，但需要较多的基础气象数据.本文综合使用以上两种模型：一部分为再分析资料和探空能够达到的最大高度以下，该部分采用积分；另一部分为再分析资料顶层以上部分，该部分采用SAAS计算.积分计算公式如下 (陈钦明等，2009；Chao,1997)：

(1)

式(1)—(3)分别为计算对流层总延迟、干延迟、湿延迟的积分公式，其中h为位势高度，N为折射率，其计算式如下：

(4)

(5)

(6)

(4)—(6)式分别为计算总折射率、干湿折射率的公式.其中，k1,k2,k3分别为77.604, 64.79和 375463 K2/hPa，p为大气压、e为水汽压、t为温度.而e又可通过以下公式计算：

e=6.1121(1.0007+3.4610-6p)g(rh,t)，

(7)

(8)

e=sp×p/0.622，

(9)

其中rh为相对湿度，sp为比湿度.(7)—(8)为利用相对湿度计算水汽压公式，(9)为利用比湿度计算水汽压的公式.SAAS模型(Saastamoinen, 1972)计算公式如下：

(10)

f(α,H)=1-0.00266×cos(2α)-2.8×10-7H，

(11)

其中α为纬度值，H为大地高.

由于再分析数据是格网数据，所以采用距离加权插值法将其进行空间插值到站点上进行计算分析(陈钦明等，2009；Chao,1997).在进行插值时，因为IGS采用的是大地高，而再分析资料的高度为位势高，所以需要将站点高度转为位势高，而正高和位势高近似，所以可将大地高转为正高代替位势高,然后以此高度为基准对周围四个格网点数据进行对流层延迟计算，最后使用(12)、(13)插值公式将临近四个格网点的值插值到站点处：

(12)

w(x,y)=x2×y2(9-6x-6y+4xy)，

(13)

x和y代表站点到格网经纬边界的距离比.

本文进行PPP解算时ZTD的值分别使用了SAAS-ZTD，再分析资料-ZTD，和参数估计值(EST-ZTD).再分析资料-ZTD将再分析资料计算得出的ZTD值作为PPP解算时的对流层延迟值.解算模型采用无电离层组合模型，该模型的待估参数含接收机坐标增量(3个)、接收机钟差改正(1个)、天顶对流层延迟(1个)、无电离层组合载波相位模糊度(X个)，待估参数总数量为5+X，观测卫星数为X，高度截止角为10°，对流层映射函数为Global Mapping Function-GMF，轨道文件钟差文件及观测值等由IGS提供.

2 实验结果

2.1 再分析资料空间分辨率的影响

本实验选取两种分辨率0.625°×0.5°, 1.25°×1°的再分析资料验证其对ZTD计算结果的影响.理论上应采取统一分辨率使实验效果最佳，但由于MERRA2的最高分辨率为0.625°×0.5°，无法与ERA5和CRA40的分辨率保持一致，所以本研究对ERA5的0.25°×0.25°分辨率进行重采样(即对高分辨率格网点数据按指定间隔进行采样，形成低分辨率格网点数据)为0.5°×0.5°和1.25°×1°，分别与MERRA2的 0.625°×0.5°和重采样的1.25°×1°计算ZTD的结果进行对比.评价指标分别为平均误差(BIAS)、平均相对误差(MRE)、均方根误差(RMS)、相对误差均方根误差(RMSREL%)，结果如表1所示.

由表1可以看出，该两种分辨率的变化对对流层延迟计算精度的影响非常小，ERA5高分辨率的RMS相对低分辨率提升0.2 mm，而MERRA2提高了0.01 mm，相对均方根误差仅分别提高了0.01%，几乎可以忽略不计.所以，本研究的后续部分统一采用CRA40(0.5°×0.5°),和MERRA2(0.625°×0.5°)以及ERA5(0.5°×0.5°)进行分析评估.

表1 不同分辨率的再分析产品计算的ZTD精度评估(参考值采用CDDIS中心提供的ZPD)Table 1 ZTD accuracy evaluation of reanalysis product calculations at different resolutions

2.2 基于GNSS的再分析资料的ZTD评估

(1) 整体精度评估

针对三种再分析资料计算的ZTD进行精度分析，由表2评估结果可看出ERA5和CRA40的平均绝对偏差比较接近，相比MERRA2分别提升了3.7和3.3 mm，而CRA40平均相对误差最小，为0.16%，ERA5和MERRA2平均相对误差分别为0.21%和0.35%, ERA5-ZTD、 MERRA2-ZTD和CRA40-ZTD的RMS分别为12.3，16.9和15.4 mm,而RMSREL(相对偏差的均方根)分别为0.53%，0.72%和0.67%.由表2的RMS计算结果看出整体精度ERA5优于其他两者，相对CRA40、MERRA2分别提高3.1和4.6 mm.

表2 三种再分析资料计算ZTD的评估结果(参考值采用CDDIS中心提供的ZPD)Table 2 Three types of reanalysis data to calculate the evaluation results of ZTD

表2也包含三者(ERA5/MERRA2/CRA40)的极值情况，分别为最大最小绝对偏差和最大最小均方根误差.其中，ERA5的极值都是最小的，最大偏差为19.5 mm，最小偏差为12.4 mm,最大均方根误差为23.4 mm，最小均方根误差为5.5 mm,而CRA40的极值是最大的，尤其是最小偏差和最大均方根误差.因此，本文从纬度和季节角度分别对三者精度进行了进一步分析.

(2) 不同纬度精度评估

图1为所有IGS站的RMS分布情况，ERA5-ZTD有91个站点在8～14 mm范围内， 而MERRA2-ZTD的RMS集中在14～20 mm之间(85个)，CRA40-ZTD的RMS主要在10～16 mm处(77个)，但CRA40-ZTDRMS值大于22 mm的站点比MERRA2多7个.

图1 ERA5/MERRA2/CRA40在IGS站点计算ZTD的RMS概率分布.纵坐标为概率(%)，即该RMS值范围内站点数除总站点数Fig.1 ERA5/MERRA2/CRA40 computes the RMS probability distribution of ZTD at the IGS site. The ordinate is the probability (%), that is the number of stations in the range of the RMS value divided by the total number of stations

图2显示了三者的RMS分布图，由图2(e、f、h)可以看出CRA40在高纬度地区的RMS比MERRA2要小，但随着纬度的降低CRA40的RMS大于MERRA2.图2(g、h、i)分别显示了三者之间的互差， CRA40和MERRA2相对ERA5在绝大多数站点都是偏大的.

图2 (a，b，c) 分别为 ERA5/MERRA2/CRA40在IGS站计算的ZTD的BIAS的全球分布； (d，e，f) 分别为ERA5/MERRA2/CRA40在IGS站计算的ZTD的RMS全球分布； (g) CRA40/ERA5-ZTD的 RMS差值分布； (h) CRA40/MERRA2-ZTD的 RMS差值分布； (i) MERRA2-ZTD/ERA5-ZTD的 RMS差值分布Fig.2 (a，b，c) are the global distribution of the absolute deviation of ZTD calculated by ERA5/MERRA2/CRA40 at the IGS station； (d，e，f) are the ZTD calculated by ERA5/MERRA2/CRA40 at the IGS station, respectively； (g) is the RMS difference distribution of CRA40/ERA5-ZTD； (h) is the RMS difference distribution of CRA40-MERRA2-ZTD；(i) is the RMS difference distribution of MERRA2/ERA5-ZTD

为进一步分析三者计算的ZTD精度跟纬度之间的关系，将125个站点分成六个区域，考虑到站点的数量分布，将纬度分为90°N—50°N (35个)，50°N—30°N (49个)，30°N—0°(11个), 0°—30°S (13个), 30°S—50°S (11个), 50°S—90°S (6个).

对比三种再分析资料可发现随着纬度的升高，RMS的整体平均值都在降低(表3).在赤道附近站点的BIAS呈现负偏差.而由表格横向比较，在90°N—30°N和30°S—90°S之间，CRA40-ZTD的RMS都比MERRA2要小1～2 mm左右，但到了30°N—30°S之间，CRA40的整体RMS值相对MERRA2反而大了2 mm左右.与上文所述的高纬度地区，CRA40的精度优于MERRA2的结果一致，反映了CRA40计算ZTD的不稳定性.总体而言，CRA40相比MERRA2计算ZTD的精度随着纬度的降低而变差.即高纬度地区，CRA40的精度相对高，而低纬度地区MERRA2精度比CRA40高.而ERA5的精度在几乎所有纬度都比两者精度高.

表3 ERA5/MERRA2/CRA40在IGS站计算ZTD的BIAS、RMS的纬度变化Table 3 Latitude changes of BIAS and RMS of ZTD calculated by ERA5/MERRA2/CRA40 at IGS stations

(3)不同季节的精度评估

考虑到大多数学者对ECMWF分析过季节性变化，本文就ERA5分析其计算的ZTD的季节性变化，并对比MERRA2/CRA40所得ZTD结果.

基于所选的125个IGS站点，分析了由再分析资料计算ZTD的季节性变化，结果如表4所示，ERA5的BIAS/RMS在一年中的变化相对较平缓，BIAS变化在0.5 mm内，RMS变化在2.6 mm内，且呈现夏秋季BIAS/RMS较高，春冬季较低的特点，而MERRA2和CRA40的BIAS/RMS在一年内的变化较大，MERRA2的BIAS年内差可达3.2 mm，RMS可达5.2 mm，CRA40的BIAS的变化可达3.3 mm，RMS可达5.4 mm.

表4 再分析资料-ZTD的季节性变化和年平均精度Table 4 Seasonal variation and annual average precision

2.3 基于探空的再分析资料的对流层延迟评估

由于IGS只提供了ZTD参考值，所以为了进一步比较三种再分析资料的相对精度情况，本文选取了全球180个探空站并使用三种再分析资料计算站点ZWD/ZHD值，并对比了再分析资料在IGS站计算结果与在探空站计算结果的相关性差异.ZTD结果如表5所示，CRA40-和ERA5-ZTD的BIAS接近，分别为8.5和8.3 mm, MRE为0.37%和0.36%,而MERRA2-ZTD与CRA40/ERA5-ZTD相比精度稍差，其BIAS和MRE分别为12.2 mm和0.53%.另一方面ERA5、MERRA2、CRA40的ZTD-RMS分别为13.2,18.7,14.9 mm,RMSREL为0.65%，0.86%，0.73%.整体上还是ERA5计算ZTD的精度最优.而针对ZHD/ZWD的计算结果表明(表5)，三者与探空站计算ZHD的精度差别不大，ERA5/MERRA2/CRA40的ZHD-RMS分别为8.2,8.5,8.2 mm,而ZWD-RMS为9.3,14.6,11.6 mm.即主要是ZWD之间的差异较大，其差异最大为5.4 mm，而ZHD最大差异为0.3 mm，也即比湿度的相对精度差异较大，结合2.2节IGS站的CRA40计算结果和MERRA2计算结果随纬度的降低而精度逐渐降低的特点可知是由ZWD评估精度变差导致.图3、4分别展示了三者计算ZWD的全球分布情况.分别对比三者的ZHD/ZWD的绝对均方根误差和相对均方根误差可看出ZHD的变化不明显，而ZWD的变化相对明显.然而由于南半球使用的站点数量少，对北半球的探空站进行了统计，90°N—50°N、50°N—30°N、30°N—0°分别有48、97、25个，表6结果与IGS站点一致，即高纬度ZTD精度优于低纬度，且探空的ZTD的精度与IGS基本一致，除在30°N—0°范围内CRA40与探空-ZTD的RMS相较于IGS-ZTD的RMS小近6 cm.

表5 探空站点计算ZTD/ZWD/ZHD的精度统计(参考值采用怀俄明提供的探空数据)Table 5 Accuracy statistics of ZTD/ZWD/ZHD calculated at sounding sites

图3 由再分析资料计算探空站的ZHD/ZWD的RMS分布(a，b，c) 分别为ERA5/MERRA2/CRA40计算ZHD的RMS站点分布(mm)；(d，e，f) 分别为ERA5/MERRA2/CRA40计算ZWD的RMS站点分布(mm).Fig.3 RMS distribution of ZHD/ZWD calculated from reanalysis data(a, b, c) Calculated RMS site distribution of ZHD for ERA5/MERRA2/CRA40 respectively (mm); (d, e, f) Calculated RMS site distribution of ZWD for ERA5/MERRA2/CRA40 respectively (mm).

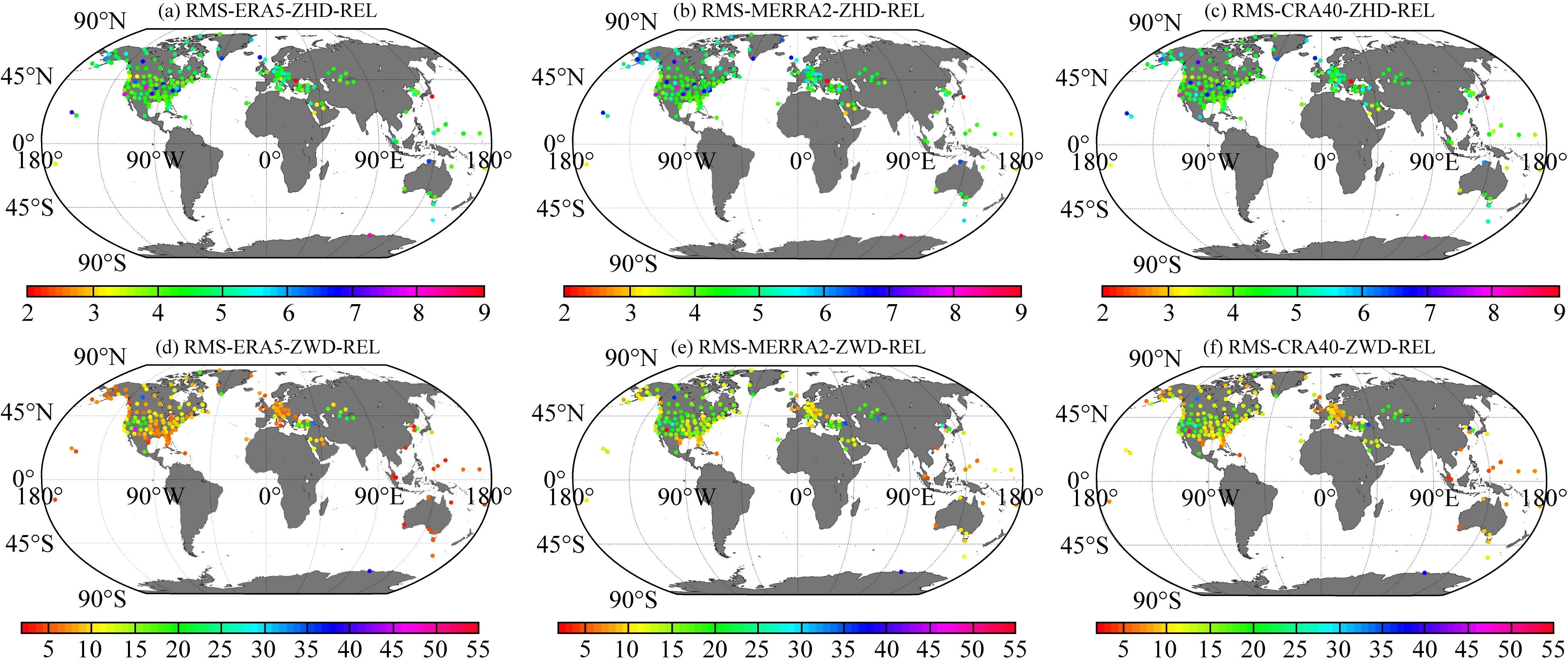
图4 由再分析资料计算探空站的ZHD/ZWD的RMSREL(a, b, c) 分别为ERA5/MERRA2/CRA40计算ZHD的RMSREL站点分布(%); (d, e, f) 分别为ERA5/MERRA2/CRA40计算ZWD的RMSREL站点分布(%).Fig.4 Calculated RMS_REL of ZHD/ZWD of sounding station from reanalysis data (a, b, c) The distribution of RMS_REL of ZHD calculated for ERA5/MERRA2/CRA40 respectively (%); (d, e, f) Calculated RMS_REL site distribution of ZWD for ERA5/MERRA2/CRA40, respectively (%).

由表2看出ERA5、MERRA2、CRA40在IGS计算ZTD的相关性系数分别为0.973、 0.960、 0.951，表5看出探空计算ZTD的相关性系数分别为0.977、0.962、0.968，由此可知再分析资料与探空站相关性强于IGS站.

2.4 精密单点定位验证

在前文所述基础上，分析引入三种再分析资料计算的ZTD对PPP定位结果的影响.在PPP解算过程中，引入再分析资料-ZTD作为已知值固定，选取JFNG(30.5156°N,114.4910°E)2020年的1、92、183、275及每天前后各一天的数据进行实验, 0表示2019年的最后一天.

由图5看出，当PPP解算过程中以传统SAAS模型为固定值时，其收敛时间最长，而将对流层湿延迟作参数进行估计(EST)时的收敛时间相对SAAS模型平均提升了72%，引入再分析资料后，ERA5/MERRA2/CRA40相对SAAS模型分别提升了66%、65%、63%.

图5 不同对流层模型精密单点定位的收敛时间(柱体从左到右依次对应图例)Fig.5 Convergence time of precise point positioning for different tropospheric models

表6 ERA5/MERRA2/CRA40在探空站计算ZTD/ZHD/ZWD的BIAS、RMS的纬度变化Table 6 Latitude changes of BIAS and RMS of ZTD calculated by ERA5/MERRA2/CRA40 at Radiosonde stations

图6和表7表明三个方向的偏差和均方根误差中SAAS模型的精度最低，在N方向EST、ERA5、MERRA2和CRA40的偏差值(BIAS)相对SAAS分别提高了75%、71%、63%、60%，RMS值分别提升62%、59%、56%、47%；在E方向偏差提升了74%、67%、67%、64%，RMS值提升了54%、51%、47%、41%；在U方向上偏差提升80%、71%、65%、61%，RMS值提升82%、81%、78%、75%.

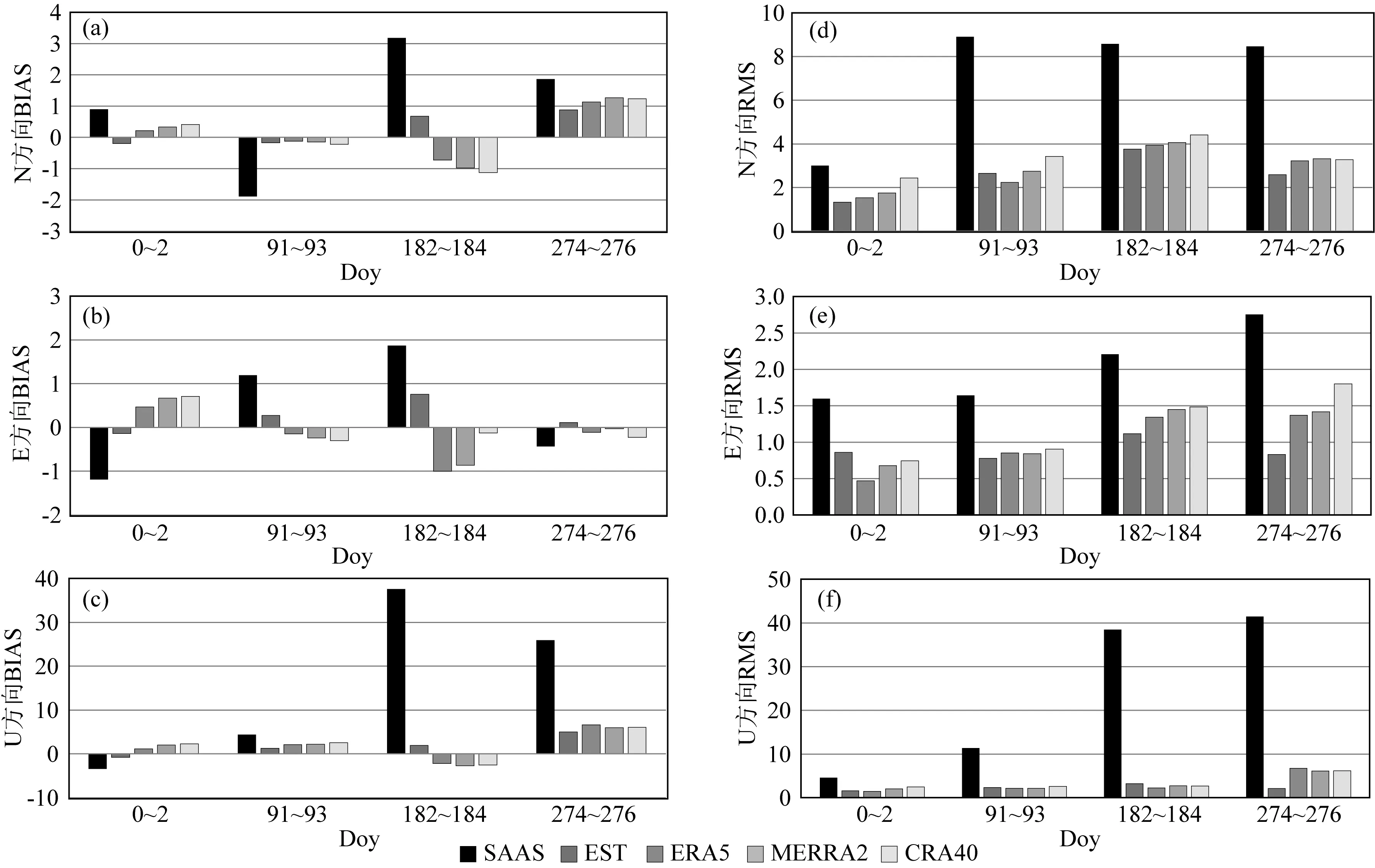
图6 不同对流层模型精密单点定位的结果比较Fig.6 Comparison of the results of precise point positioning for different tropospheric models

表7 定位结果的偏差和中误差Table 7 RMS and bias of localization results

可知，加入再分析资料后的PPP解算相对传统的方式(SAAS)有了很大提升，其在N、E方向上精度与收敛时间与EST相近，在U方向上与EST有一定差异，主要是由于再分析资料计算ZTD的精度差异导致.

3 总结

本文以IGS提供的ZTD值和由探空站数据解算的ZTD/ZHD/ZWD值为真值，对三种再分析资料(ERA5、MERRA2、CRA40)进行了精度分析，并验证其在PPP中的适用性，得出以下结论：

(1) 以IGS站为真值时，三者中ERA5的精度最优，CRA40和MERRA2次之.考虑纬度因素时，三者都随着纬度的降低，精度逐渐降低，进一步区分纬度区间后，发现CRA40在中高纬度地区即南北纬30°以上比MERRA2优，但在南北纬度30°之间时，MERRA2的精度相对CRA40较优.且三者都表现出与季节的相关性，在夏秋季的RMS值大于春冬季.

(2) 以探空为参考值时，分析了ZHD和ZWD的精度.发现三者的ZHD精度相当，RMS值差值最大为0.3 mm，BIAS值最大相差0.5 mm.而ZWD的RMS最大相差5.4 mm，BIAS最大相差3.5 mm.整体而言ERA5的精度最高，变化最稳定，其次是CRA40和MERRA2.

(3) 使用三种再分析资料计算的对流层延迟作为辅助进行PPP解算，在收敛时间上相对于SAAS模型都有提升，且在定位精度上相对于SAAS在三个方向(N、E、U)上的RMS都有一定的优化.其中，ERA5提升精度最高.由此可知，再分析资料的对流层延迟对PPP定位结果有较好提升效果.