载瘤动脉双向流固耦合动力学数值模拟分析

王得辰， 张俊婷， 樊佳伟

(太原科技大学 应用科学学院， 山西 太原 030024)

0 引 言

动脉瘤是由于动脉壁的病变或损伤而出现的动脉壁局限性或弥漫性扩张或膨出， 这类疾病有着较高的发病率及死亡率。 研究表明， 动脉瘤的生长、 破裂与动脉血流特征有关[1]。 相关研究表明[2-12]， 血流动力学因素的异常改变是动脉瘤破裂的重要因素之一， 在相同的动力学模型下， 血流动力学不仅与动脉瘤的形状、 大小、 位置、 动脉瘤颈口大小等有关， 也与载瘤动脉的直径、 瘤壁厚、 弯曲度及弹性模量等有关。 人体内的血管外部被组织液所包围， 这些液体会对血管外壁产生外压力， 最终可能会导致实验模拟计算的数值小于实际值[6]。 因此， 本文对载瘤动脉的弯曲度、 动脉瘤高等与动脉血流动力学特征的关系进行有限元数值模拟和探讨， 旨在发现线弹性条件下影响动脉瘤破裂的血流动力学因素， 为临床提供参考。

1 动脉载瘤模型的建立

1.1 双向流固耦合力学模型

血液在血管中流动的流动方程可用Navier-Stokes方程[13]来描述。

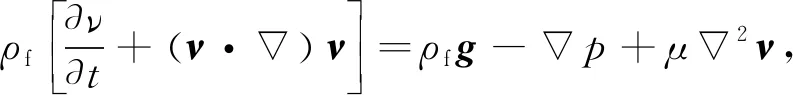
(1)

式中：ρf为血液密度；t为时间；ν为速度矢量；g为重力加速度矢量；p为压力；μ为黏性参数。

动脉瘤组织控制方程为

ρsas=·σs,

(2)

式中：ρs为动脉管壁密度；as为管壁质点加速度；σs为血管及血管瘤的应力张量。

血液在血管中流动还要满足连续性方程， 对于不可压缩流体可表示为

·ν=0.

(3)

在流固耦合交界面上， 变量的传递方程[14]应满足

ds=df,

(4)

τs·ns=τf·nf,

(5)

μs=μf,

(6)

式中：ds为固体的位移；df为流体的位移；τs为血管及血管瘤的剪切力矢量；τf为血液的应力张量；ns为固体边界法向量；nf为流体边界法向量；μs为固体摩擦系数；μf为液体摩擦系数。

1.2 模型的建立及部分属性

图1 为不同弯曲度下的载瘤动脉模型网格图。 根据磁共振血管线(MRA)影像及文献[15]， 设载瘤动脉长度为100 mm， 瘤的位置在50 mm 处， 其外半径为8 mm， 壁厚与血管壁厚相同； 血管外半径设为4 mm， 壁厚为1 mm。 血液密度为1 060 kg/m3， 动力粘度为0.003 5 Pa·s。 运用SolidWorks三维建模软件生成图1 所示模型。 采用网格尺寸为0.8 mm的固定值网格划分方法进行网格划分。

(a) 弯曲度α=150°

1.3 边界条件的设置

流体的流动状态有层流和紊流， 雷诺数Re是判断流体流动状态属于层流还是紊流的依据， 其公式[16]为

Re=(ρfvD)/μ,

式中：ρf为血液密度；v是血液速度；D，μ分别为血管直径和血液动力粘度。 根据文献[17]， 动脉内血流速度约为0.1 m/s～0.95 m/s， 雷诺数约为500～700。 流体为层流状态时雷诺数小于2 000， 当雷诺数介于2 000～4 000之间为过渡状态， 当雷诺数大于4 000时为紊流状态， 所以， 血液在动脉瘤中的流动状态为层流状态。

文献[18]表明， 当血管直径>0.5 mm时， 用牛顿流体代替非牛顿流体的误差不会超过2%。 本文所设定的载瘤动脉模型直径为8 mm， 因此， 视血液为牛顿流体。

动脉瘤壁及血管壁视为线弹性材料， 弹性模量为5 MPa[19]， 泊松比为0.45[14]， 载瘤动脉的入口和出口设为固定支撑[20]。

入口速度边界条件如图2 所示[21]， 出口设置为压力出口， 压力为正常血压13 330 Pa。

图2 入口速度边界条件[21]

2 数值模拟结果分析

2.1 不同弯曲度下动脉瘤数值模型对比分析

图3 为不同弯曲度的载瘤动脉在不同时刻的速度流线图。 由图3 可以看出， 在1个心动周期内， 动脉瘤内血液呈螺旋状流动状态。 在近1/4心动周期时刻动脉瘤内血流量相对较少； 在近1/3心动周期内， 均可发现在动脉瘤底部出现了1处较紊乱的流动， 这可能是由于1/3周期内载瘤动脉血流量增大， 且血流速度减小造成的； 在整个心动周期的最后时刻， 动脉内血液流动趋于稳定。与其他时刻相比， 由于血管弯曲， 其内壁底部的血液流速明显高于内侧的流速。 载瘤动脉弯曲程度较大时， 血液撞向血管内壁时， 返回的血液穿过弯曲部位的内侧， 导致内侧血流速度较大。 血液从入口处沿着动脉血管的内壁流动， 经过动脉瘤时速度变慢且沿着动脉瘤壁进入动脉瘤内部。 当血液再由动脉瘤内部进入血管时， 速度加快， 在动脉瘤内部形成涡流。 对比图3(a)、 图3(b)和图3(c)可以看出， 图3(c)在动脉瘤腔的速度差比图3(a)和图3(b)变化大， 更容易形成涡流且血液流动较为紊乱， 从而增大了动脉瘤破裂的风险。

图3 单个心动周期内不同弯曲度载瘤动脉在不同时刻的速度流线图

图4 为不同弯曲度载瘤动脉在不同时刻的Mises等效应力云图。 由图4 可以看出， 在近1/4心动周期时刻， 由于进入动脉瘤腔内的血流速度较大， 对动脉瘤壁的冲击也较大， 应力也随之达到最大。 在半个心动周期， 随着血流量的增多和血流速度的减小， 最大应力减小， 最小应力增大。 在整个心动周期内动脉瘤两侧的应力比其他部位的大。 另外， 比较图4(a)、 图4(b)和图4(c)可以看出， 最大应力的位置都出现在动脉瘤与血管连接处的前后两端， 弯曲度较大的载瘤动脉的动脉瘤腔内的应力分布比弯曲度较小的载瘤动脉的动脉瘤腔内的应力分布更不均匀。

图4 单个心动周期内不同弯曲度的载瘤动脉在不同时刻的应力分布

图5 为不同弯曲度载瘤动脉在不同时刻的变形云图。 在1个心动周期内， 动脉瘤的变形先增大后减小， 这是由于血管弯曲会改变血液的流动状态， 血液的流动反过来作用于血管壁[8]而造成的。 比较图5(a)、 图5(b)和图5(c)可知， 随着弯曲度的增加， 动脉瘤的变形程度增大， 更容易发生形变； 当弯曲度减小时， 动脉瘤瘤体的变形与瘤颈处的变形之比逐渐增大， 即在动脉瘤顶部更易发生形变。 因此， 弯曲度较大的载瘤动脉上的动脉瘤发生破裂的风险较大。 此外， 结合图2 和图5 还可知， 血液速度在0.2 s左右时达到最大， 但动脉瘤的最大形变却在0.26 s左右出现， 这是因为血液流动的动能转变为使血管变形的弹性势能， 从而导致此种现象的出现。

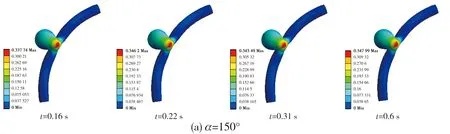
图5 单个心动周期内不同弯曲度载瘤动脉在不同时刻的变形分布

图6 为载瘤动脉在不同弯曲度下Mises等效应力和瘤内压力随时间的变化图。 由图6(a) 可以看出， 当弯曲度较小时， 载瘤动脉最大应力在达到某最大值后呈稳定状态且在1/4周期时刻， 压力和应力都达到了最大值， 之后随着时间推移， 压力和应力都有所减少且变化相对平稳； 当弯曲度较大时， 其上最大应力和动脉瘤内压力呈周期性波动， 变化更加频繁， 反复的应力变化将导致动脉瘤承受应力的能力大幅下降， 更容易在最大应力点处破裂。 由图6(b) 可以看出， 在1/4周期时刻， 载瘤动脉弯曲度越大时， 动脉瘤的压力越大， 越容易破裂。

(a) 应力随时间的变化

2.2 不同瘤体高度数值模拟分析

由文献[22-25]可知， 瘤体高度/血管管径比值(SR)与动脉瘤破裂存在明显的相关性， 且其大小可较好预测动脉瘤破裂的可能性。 同时， SR值容易测量和获得， 分析较简单， 故本研究选择了血管管径相同， 瘤高h分别为11 mm， 12 mm和14 mm的动脉瘤模型。 3个动脉瘤的SR值分别为1.25, 1.5, 1.75。

图7 为单心动周期不同瘤高载瘤动脉在t=1 s时的速度流线图。 由图7 可以看出， 血液在3种瘤高的动脉瘤内都呈螺旋状流动。 对比图7(a)、 图7(b)和图7(c)可知， 随着瘤高增加， 动脉瘤处的血流速度差增大， 血液流动也更加紊乱， 越容易形成涡流， 从而更容易导致动脉瘤的破裂。

图7 单个心动周期不同瘤高载瘤动脉在t=1 s时的速度流线图

图8 为单个心动周期在t=1 s时不同瘤高载瘤动脉的Mises等效应力云图。 由图8 可以看出， 不同瘤高的载瘤动脉的最大应力位置都出现在动脉瘤与血管连接处的前后两端。 对比图8(a)、 图8(b) 和图8(c)可知， 动脉瘤内的Mises等效应力随着动脉瘤瘤高的增大而减小， 且最大应力值与最小应力值的差值也越来越小。 由此说明， 随着瘤高的增加， 载瘤动脉中的应力分布变得更加均匀。

图8 单个心动周期内不同瘤高的载瘤动脉在t=1 s时的Mises等效应力云图

图9 为单个心动周期在t=1 s时不同瘤高载瘤动脉的变形云图。 由图9 可以看出， 不同瘤高的载瘤动脉最大变形位置均在动脉瘤底部， 且动脉变形均集中在动脉瘤底部附近， 从底部沿着动脉瘤向上， 变形越来越小， 动脉瘤两侧变形最小。 另外， 比较图9(a)、 图9(b)和图9(c)还可以发现， 随着动脉瘤瘤高的增大， 动脉瘤腔内的压力变大， 变形增大。

图9 单个心动周期(t=1 s)不同瘤高的变形云图

图10 为不同瘤高时 Mises等效应力和瘤内压力随时间的变化图。 由图10(a)可以看出， 随着瘤高的增加， 动脉瘤腔内最大应力也随之降低， 动脉瘤腔内的应力分布更加均匀。 由图10(b)可以看出， 3种情况的动脉瘤瘤内压力都在1/4周期时刻达到了最大； 管径相同的情况下， 动脉瘤高度越高所承受的管壁压力越大， 越易引起动脉瘤的破裂。

(a) 应力随时间的变化

3 结 论

本文建立了不同弯曲度的载瘤动脉双向流固耦合数值模型以及不同瘤高的动脉瘤模型， 应用流固耦合分析方法研究了线弹性载瘤血管与不可压缩黏性血液的相互作用对动脉瘤血流特性参数及瘤体受力变形的影响， 分析了动脉瘤中血液流动的流场变化以及动脉壁、 瘤壁的变形和应力， 根据分析得出了动脉瘤内的血流特性， 可为动脉瘤破裂预测提供更有效的依据。 主要研究结论有：

1) 不同弯曲度的载瘤动脉， 在 1/4 周期时刻动脉瘤内的血流量较小， 变形达到最大； 在近1/3周期时刻动脉瘤底部出现较为紊乱的血流； 在整个心动周期的最后时刻(t=0.6 s)血流相对稳定；

2) 随着弯曲度的增加， 动脉瘤内应力梯度增大， 变形程度也增大， 更容易发生形变； 弯曲度较小时， 动脉瘤内血液流动相对紊乱， 但其内部的应力分布较为均匀；

3) 随着瘤高的增高， 动脉瘤下半部的应力增大， 同时动脉瘤的变形也增大； 在单个心动周期， 随着时间变化， 瘤壁应力变得平缓， 但动脉瘤内的血液流动较紊乱。

本文对临床胸主动载瘤动脉危险部位的预测有一定帮助， 可以为临床诊治提供依据。 但由于临床所见的动脉瘤不一定是标准的球体以及软件本身计算所存在的偏差， 所以会导致实际分析的结果发生变化， 今后的研究将进一步完善载瘤动脉模型。