考虑能量回收的露天矿新能源卡车路径规划

顾清华 刘绒绒 李学现 高 松

(1.西安建筑科技大学资源工程学院,陕西 西安 710055;2.西安市智慧工业感知计算与决策重点实验室,陕西 西安 710055;3.西安建筑科技大学管理学院,陕西 西安 710055)

在油耗法规加严、环保要求提高、常规车限行以及新能源相关技术的进步、成本下降、市场接受度的提升等情况下,新能源化成为卡车发展的未来趋势。近年来新能源卡车在露天矿开采运输中得到了很大的发展。第一届中国国际智能网联与新能源卡车大会提出,新能源卡车可优先应用于矿区、港口两大场景。因为,这两个场景下的卡车运输多为中低速运行,长时间低速行驶更容易增大油耗[1],而新能源卡车在减速、制动、滑行等状态下可以进行能量回收,继而大幅降低运营成本。但是新能源卡车在矿区的应用还存在一些不足,如里程焦虑等问题,都制约着新能源卡车在矿区的发展。在现有电池技术上,利用露天矿作业面的高差,进行合理的路径规划减少里程焦虑成为了一个新的发展方向。

露天矿路径问题长期以来始终都是露天采矿技术研究和领域中的一个热点问题,目前国内外学者对该问题的研究主要集中于以下2 类。

第一类,对矿山初始运输道路的开拓定线。ADENSO-DIAZ 等[2]从露天煤矿运输系统布置过程中的波动变化入手,提出了一种用于自动更新静态道路网络基有向图的新方法,实现煤炭运输路线的优化;朱明海[3]基于成本理论提出了道路价值模型,利用遗传算法对矿山道路进行智能三维选线;Choi 等[4]开发了一种新的基于栅格的GIS 模型,对影响道路规划的因素赋以不一样的权重来生成平均不利分数网格,以最小化成本为目标确定最优路径;之后Choi 和Nieto[5]在铺设和未铺设临时道路的工作区域,考虑沿线地形起伏和曲线对路径规划的影响,改进了最小成本路径算法;刘光伟等[6]采用时变运输功作为运营成本的评价指标,基于采场内运输系统的时空演化特性提出了全新的道路选线及线路更新判别算法。

第二类,对既有运输道路利用群智能算法寻优。Chen Y 等[7]创建带权无向图,对传统Dijkstra 算法进行改进,以运距为评价指标来求解最优路径;孙臣良等[8-9]考虑道路等级、高差等影响因素扩大粒子群搜索范围的改进粒子群求解露天矿最短路径;柴森霖等[10]基于改进遗传算法提出了动态路径规划,以此来描述露天矿路网的随机波动性,并求解运输功最小化的路网优化模型;Sun B 等[11]通过路径与障碍物的距离,划分不同的速度段,考虑到安全行驶,规划出更加符合实际情况的路径;顾清华等[12]基于IAS 算法,以油耗成本和碳排放成本最小化为目标,建立了运输优化模型;Liu C 等[13]实现了路径长度和行驶安全之间的平衡;顾青等[14]设计的能耗预估代价函数,求解了能耗最小为目标的最优路径。

在上述研究成果中,国内外学者对露天矿的路径规划已经逐渐由基于距离为目标转换为以成本或者能耗为目标求解最优路径。目前,新能源卡车的路径优化主要是以电池电量为约束的路径规划,以及最优的充电路径规划[15-17]。新能源卡车的能量回收分为两大类:制动、滑行能量回收。通过踩制动踏板实现能量回收就是制动能量回收,仅依靠丢油门实现能量回收则叫做滑行能量回收[18-19]。然而,在露天矿作业环境下,由于不同的路径有不同的坡度,因此相同长度的路径也可能有着不一样的能耗。同时,在卡车的实际运输过程中存在路程较长的时候需要中途充电的情况。为减少里程焦虑,基于能量优化进行露天矿新能源卡车的路径规划是十分有必要的[20]。对于露天矿这种特殊的作业环境,为了更精细化地反映卡车的实际运输状态,通过真实的路网平面图对露天矿路网进行建模。综合考虑卡车行驶速度、车载质量、路段坡度、道路等级这4 个因素,计算势能、行程阻力能量损耗、电机损耗以及再生制动能量回收。针对里程焦虑问题,考虑卡车初始SOC、能量消耗、能量回收等因素,建立以最小化电池能耗为目标的露天矿最优路径规划模型,并利用IA∗算法进行求解。最后以山西省某露天矿为实例,证明能量优化模型的有效性。

1 问题模型

新能源卡车行驶过程中,制动状态下会进行能量回收,将势能转化为电能存储进电池里进行重复利用,而不是被摩擦阻力消耗掉[21]。本文假设卡车只在起点启动,终点和滑坡等状态时发生制动,路途中将不考虑紧急制动和再启动造成的能量消耗和能量回收。由于露天矿的道路复杂,道路质量参差不齐,因此卡车在运输过程中能耗和能量回收也不稳定[19]。为解决这些问题,首先根据露天矿的道路信息建立运输道路路网模型,然后考虑能量回收和利用建立能量优化模型,最后利用IA∗算法求解最小能耗为目标的能量优化模型。

1.1 模型假设

为了建立更加精确的问题模型,做出如下假设[22-23]:①卡车在相同等级的道路上具有相同的平均行驶速度;② 每一路段之间的坡度由首尾两点之间的高差确定;③装载点的车辆可以向不同的卸载点运送矿石;④ 暂时不考虑温度和驾驶员风格对耗电量的影响;⑤ 默认卡车在电量小于规定值时不再运行开始充电;⑥ 新能源卡车为同一型号,且载重量一致;⑦ 路途中将不考虑紧急制动和再启动造成的能量消耗和能量回收。

1.2 能量优化模型

建立的露天矿新能源卡车运输能量优化模型如下:

式中,AE为总能耗,J;Ac(ij)、Ag(ij)、At(ij)与Am(ij)分别为在路段(i,j)上势能、行程阻力、电机损耗和再生制动回收的能量消耗,J;Lij为路段(i,j)上的实际运输距离,m。

车辆沿路径Mn(m1,m2,…,mn)行驶的总能耗为

式中,mi表示节点i;n为路径数量。

1.2.1 势能

当车辆在路段(i,j)上行驶时,一部分电能会转换为势能消耗掉,记为

式中,G为新能源卡车的有效荷载,kg;θ为行驶过程中与水平地面的夹角。

1.2.2 行程阻力能量损耗

在驾驶电动汽车的过程中,车辆会受到路面的摩擦阻力、坡度阻力、空气阻力、轴承之间的摩擦等,通过力学分析,可以得到以下方程:

式中,F为电动汽车的牵引力;Ff为摩擦力;m为卡车质量;a为加速度。

摩擦力Ff主要包括空气阻力Fa、坡度阻力Fp、滚动阻力Fr和轴承之间的摩擦力Ft。

式中,ρ为空气密度,kg/m3;CD为空气阻力系数;Af为卡车的迎风面积,m2;νij为车辆在路段(i,j)上的平均速度,km/h;μ为坡度阻力系数;ff为滚动阻力常数;g为重力加速度;b为轴承阻尼系数;Rr为车辆轴承中径,m。

因此,新能源卡车实际行驶路段Lij的行程阻力能耗为

1.2.3 电机损耗

新能源卡车在运输过程中,除了势能以及行程阻力的能量损耗,还有辅助电源、电机等的损耗。具体主要是指电机内部的铁损、铜损与线损。可以描述如下:

式中,I和r分别为电枢的电流和电阻。该力是由电机转矩产生的,可以简化为电枢常数、磁通量和电流的乘积[17]:

式中,Fb为再生制动力;T为转矩;ka是电枢的常数;φd为磁通量;Rt为车辆轮胎半径,m。

根据以上分析,得到电机功耗表达式:

1.2.4 再生制动能量回收

在制动过程中,电动汽车通过再生制动系统回收部分电能,从而有效延长续驶里程。再生制动功率可描述如下:

式中,ϑ为电机的功率[24]。当Lij是下坡路段时,则势能会转换为电能存储起来,因此得到的能量为

1.3 考虑充电桩的能量优化方法

根据1.2 节所提出来的能量优化模型,利用IA∗算法求解,从起始节点到终止节点找到最小能耗的一条路径,从而实现能量优化。但是由于里程焦虑的问题,新能源卡车不能保证每次电池的SOC 能满足里程消耗。因此,为了减少里程焦虑问题,应该合理考虑充电桩的位置。

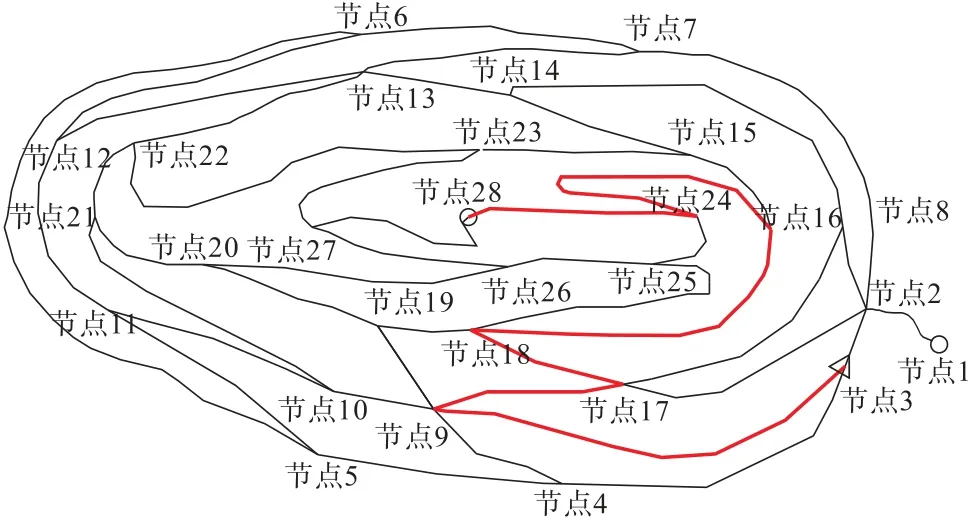
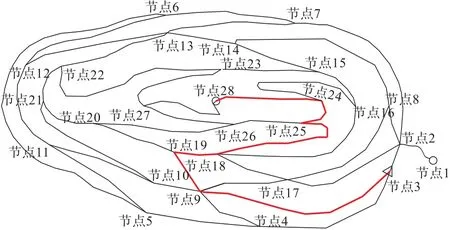
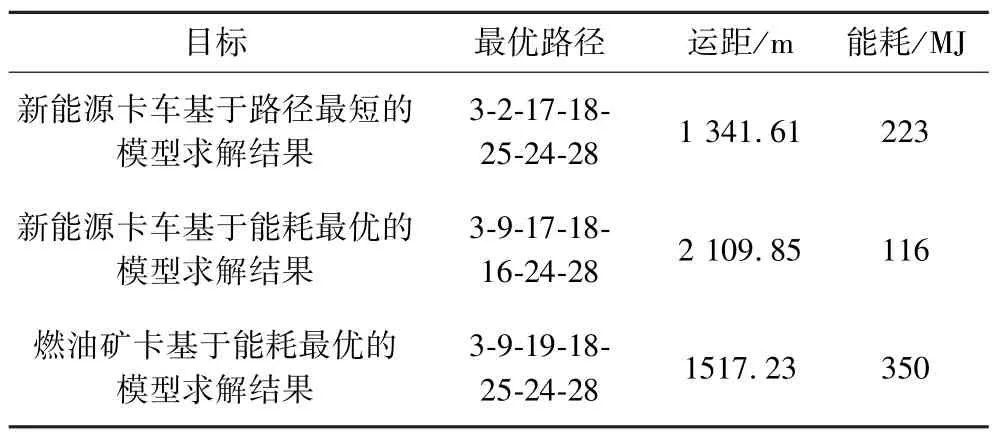
当车辆出发前,记录卡车当前SOC,记为S。利用IA∗算法计算从起始点到终止节点的最小能耗,记为Emin。比较S和Emin:①S>Emin,卡车按照计算Emin的路径行驶;②S

由于第二种情况下,当前电量不能支撑车辆走完全程,此时考虑充电桩的位置,记录充电桩位置为节点Ci。基于IA∗算法计算起始节点到充电桩Ci的i条路径的能耗,充电完成后,计算充电桩Ci到终止节点的i条路径的能耗。此时整段路程分为两部分,第一部分是从起始节点到充电桩,第二部分是充电桩到终止节点,整段路程的能耗为第一部分和第二部分的组合值。依次分别计算充电桩{C1,C2,...,Ci}为节点时的能量消耗,选择最小能耗组合值时的充电桩作为充电节点。具体流程如下:

图1 考虑充电桩位置的最优路径方法流程Fig.1 Flow chart of optimal path method considering charging pile position

2 算 法

考虑了露天矿的特殊性,提出了一种基于能量优化求解路径规划的IA∗算法,该算法利用基于角度的搜索策略,提高算法的搜索速度。

2.1 搜索区域确定

将搜索区域露天矿地形图简化为2 维数组[5]。将露天矿各个节点放在正方形格子里,将格子分为可行和不可行。格子的中心称之为节点,计算各相关节点之间的行驶代价。从起点开始检查相邻节点,然后向四周扩展,直至找到目标。

2.2 搜索策略

2.2.1 代价估计值的计算

利用代价估计函数f(n)来评估节点之间的行驶代价:

式中,g(n)为起始节点到状态节点的实际代价;h(n)为状态节点到终止节点的预估代价。得到最优路径的关键是状态节点的选择,也就是h(n)的选取,用p(n)来表示状态节点到目标节点的距离,有以下3种情况:①如果h(n)p(n),搜索节点少,搜索范围小,效率高但容易陷入局部最优,不能保证一定找到最优路径。

A∗算法中,有2 个储存数据信息的列表,分别为开放列表和封闭列表,被考虑的节点放入开放列表,不被考虑的节点放入封闭列表。对于每一个节点都有一个代价估计值f(n),利用代价估计值,从起始节点一直遍历到终止节点,从而找到最优路径。

2.2.2 基于角度搜索策略

传统的A∗算法在寻找后续节点时,选择了相邻8 个节点进行搜索。为了提高搜索速度,提出了一种基于角度的双向搜索策略,将节点用网格表示,搜索过程如图2、图3 所示。

图2 A∗算法传统的搜索方式 Fig.2 The traditional search mode of A∗algorithm

图3 改进A∗算法的搜索方式Fig.3 Improved search mode of A∗ algorithm

(1)确定起始节点和终止节点。

(2)利用起始节点和终止节点的位置坐标信息,将起始节点相邻的节点分为4 个区域。

(3)此时对搜索区域进行筛选,将传统的8 个节点的搜索范围改进为位于区域1、区域2、区域3 的节点放入开放列表,朝着终止节点方向进行搜索。

(4)同理,将终止节点基于角度划分的区域,向起始节点方向进行搜索。

如上图所示,传统的A∗算法将起始节点的8 个相邻节点,分别计算起始节点到状态节点的g(n)值和状态节点到终止节点的h(n)值。利用角度策略改进的搜索方式,主要创新点是基于目标方向的角度信息将搜索区域分为4 个区域,选择区域1、区域2、区域3 这3 个靠近目标节点的方向进行节点搜索,利用双向搜索策略和搜索区域筛选的结合,提高搜索速度。

2.3 搜索流程

开始搜索之前,所有的节点存在3 种状态,状态1 在开放列表里,状态2 在封闭列表里,状态3 既不在开放列表里,也不再封闭列表里。搜索步骤如下:

(1)从起始节点开始,搜索靠近目标节点的方向的相邻节点,此时将起始节点和可到达的相邻节点都记为状态1,放入开放列表。

(2)此时上一个节点就为下一个节点的父代节点,计算父代到各个子代节点的代价估计值,用来选取下一个父代节点。

(3)出现新的父代节点,就将上一个父代节点由状态1 变为状态2。状态2 中的节点是不再进行检查的节点集。

(4)重复上述步骤,直到找到最优路径。

3 仿真分析

采用仿真实验来验证模型合理性和有效性。图4为露天矿路网平面图,其中每个节点代表一个路口,节点间的连线代表路段。图5 为所提取出来的路线图,可以看出每个节点还具有一定的海拔高度。在路网中总共有28 个节点,包括2 个充电站,标记为Ci。起点标注为Δ,终点为○,仿真参数如表1 所示。采用2 个仿真实验来验证能量优化模型的合理性和有效性。

表1 仿真参数Table 1 Simulation parameters

图4 露天矿路网平面图Fig.4 Plan of open-pit mine road network

图5 露天矿路线提取图Fig.5 Extraction map of open-pit mine route

3.1 仿真实验1

首先,为了验证能量优化模型的有效性,对新能源卡车和燃油卡车有效荷载状态下从起始节点到终止节点分别以能耗最小和路径最短为目标进行最优路径规划。在本实验中,设置起始节点为节点3,终止节点为节点28。利用IA∗算法,分别对基于最短运输距离和最小运输能耗的2 个模型求解,求解结果如表2 所示,求解结果可视化如图6、图7、图8、图9所示。

图6 新能源卡车基于最短路径的路径规划Fig.6 Path planning of new energy truck based on shortest path

图7 新能源卡车基于能耗最少的路径规划Fig.7 Path planning of new energy truck based on the least energy consumption

图8 燃油卡车基于能耗最少的路径规划Fig.8 Path planning of fuel truck based on the least energy consumption

图9 能量消耗可视化Fig.9 Visualization of energy consumption

表2 能量优化模型求解结果Table 2 Solution results of energy optimization model

将3 种模型的计算结果两两进行对比,对于新能源卡车基于最短运输距离的路径规划,路径长度为1 341.61 m,能耗为223 MJ。基于能量优化的路径规划,路径长度为2 109.85 m,能耗为116 MJ。由于露天矿新能源卡车的使用,我们的最终目标是能量优化,虽然路径3-2-17-18-25-24-28 运输距离更短,但是该路径的能量消耗却远远超过路径3-9-17-18-16-24-28。因此,在进行新能源卡车路径优化时,选择道路等级较好,坡长较长的运输路线,进行有效的能量回收,对能量优化更有利。

燃油矿卡基于能耗的路径规划,路径长度为2 109.85 m,能耗为350 MJ,是3 种模型里能量消耗最多的,主要原因是由于燃油卡车不能进行能量的回收利用,让制动产生的能量由摩擦发热浪费掉,而不是像新能源卡车一样储存在电池里,进行能量的回收利用。

3.2 仿真实验2

为减少运输过程中的里程焦虑问题,我们在运输过程中考虑充电桩的位置。在本研究中考虑该区域路网的2 个充电桩C1和C2。起始节点选择为节点2,新能源卡车初始SOC 满足到达任意一个充电桩的能耗。考虑能量消耗,利用IA∗算法对考虑里程焦虑问题的能量优化模型进行求解。结果如表3 所示。

表3 考虑充电桩位置的路径规划Table 3 Path planning considering charging pile location

根据模型求解结果,在考虑里程焦虑问题上,选择充电桩C2进行充电。从起始节点到充电桩C2的基于能耗的最优路径如图10 所示标为虚线,从充电桩C2到终止节点的基于能耗的最优路径如图10 所示标为粗实线,根据2.3 小节的考虑中途充电的能量消耗路径规划的选择方法,结果显示如图10 所示。实验验证,在实际情况中电池初始SOC 不足以支撑卡车运行全程时,考虑充电桩的位置进行基于能耗最小的路径规划是有意义的。

图10 考虑充电桩位置的能量最优路径规划Fig.10 The energy optimal path planning considering charging pile location

4 结论

本研究考虑了新能源卡车在运输过程中的势能消耗,行程阻力消耗,电机损耗和再生制动能量回收,建立了以能耗最小为目标的露天矿新能源卡车能量优化模型,并用IA∗算法对问题模型进行求解。主要结论如下:

(1)根据车辆运行时能耗情况,建立了能量优化模型,对IA∗算法改进,提出了一种考虑充电桩位置的新能源卡车运输路径规划方法。

(2)利用基于距离和基于能耗的能量优化模型求解最优路径,实验结果验证了距离最短不一定能耗最小,利用矿井作业高差进行能量回收是切实可行具有实际意义的。利用燃油卡车和新能源卡车就能耗最小求解问题模型,新能源卡车能量优化模型在露天矿运输过程中有着更少的能耗,证明新能源卡车在露天矿运输的应用中成为趋势。

(3)所提出的问题模型,可以用于充电站的选择,仿真实验表明能耗更小的路径并不一定运输距离也小,因此基于能耗建立的模型才更符合实际需要。在新能源卡车初始SOC 不足时,采用能量优化方法可以得到经过充电桩的最优路径,既能保证运输的完整性又能保证能耗最少,从而减少里程焦虑。