不同固定碳含量石墨矿石单轴压缩力学行为及损伤本构关系研究

李兴旺 叶海旺 雷 涛 李 宁 王其洲 王炯辉 赵明生

(1.武汉理工大学资源与环境工程学院,湖北 武汉 430070;2.矿物资源加工与环境湖北省重点实验室,湖北 武汉 430070;3.五矿勘查开发有限公司,北京 100044;4.保利新联爆破工程集团有限公司,贵州 贵阳 550002)

岩石是一种天然材料,由于赋存环境和成岩机理的差异,不同种类岩石材料的矿物组分和微细观结构特征具有显著差别。如何确定岩石力学性质参数与其矿物组分和微细观结构之间的定性、定量关系,对于深刻认识岩石力学性质变化规律和科学利用岩石材料具有重要意义[1]。

诸多学者就岩石矿物组成和细观结构与其力学特性之间的关系进行了大量研究[2-4],并指出岩石矿物组分及微细观结构特征是决定其物理力学性质的主要因素。通过对力学参数的定性和定量分析,左建平等[5]认为高强度矿物含量较低时对岩石整体力学性质的影响并不明显,只有含量超过某一阈值后才有较大影响;而软弱矿物含量的减少,则会导致玄武岩的宏观力学行为发生显著变化。陈江峰等[6]通过单轴压缩试验,研究了矿物组分对泥岩力学性质的影响,并发现随着石英含量增高,泥岩的单轴抗压强度和弹性模量均呈增大趋势;而随着黏土矿物含量的增加,其规律则相反。钟建华等[7]认为页岩中的鳞片状黏土矿物片理中存在的不规则碎屑颗粒和自生矿物,会降低软弱面的抗压和抗拉强度。孙彪等[8]在对页岩的脆性评价和影响因素分析中,认为随着方解石含量的增加,灰质泥岩杨氏模量减小,泊松比增加,脆性越来越弱。余坤等[9]也发现不同脆度的矿物在不同程度上控制着页岩的力学性质。Li Qian 等[10]在大量岩石样品矿物含量、矿物粒径、研磨性和硬度等测试结果的基础上,利用原始测试数据与反向传播人工神经网络(BP-ANN)建立预测函数,揭示了矿物含量和粒度对岩石研磨度和硬度的影响规律。

上述研究针对各类岩石矿物组成和细观结构对其力学性质的影响而展开,取得了很多有益的成果。但目前针对岩石矿物组分对其损伤本构关系影响的研究还少见报道,针对石墨矿石本构关系的研究更是鲜少涉及。石墨作为我国重要的战略性矿产资源,在国防、航天、新材料等领域占有重要地位。随着现代科学技术和工业的发展,石墨的应用领域正不断拓展,已逐渐成为高科技领域中新型复合材料的重要原料,在国民经济中具有举足轻重的作用[11]。因此,实施科学合理精细的石墨资源开发利用策略,关乎国家传统工业和战略性新兴产业可持续发展大局。由于石墨矿石特殊的成岩环境和沉积过程形成了其独特的矿物组成规律和微观结构特征,不同固定碳含量的石墨矿石在岩石力学性质、工业价值以及开发利用难易程度等方面均有较大差异。因此,研究不同固定碳含量石墨矿石的力学性质及其损伤本构关系,一方面能为石墨资源精细化开采方案的设计与实施提供理论支撑,另一方面也是对岩石矿物组分与其损伤本构关系内在关联的有益探索,兼具重要的理论意义与实际价值。

既然岩石矿物组分对其力学性质的影响可认为是不同强度矿物含量变化和矿物嵌布特征差异共同作用的结果。那么,是否可以将这种影响在岩石损伤本构关系的研究中加以考虑,以建立能反映岩石矿物组分影响的损伤本构模型呢? 鉴于上述原因,本文以不同固定碳含量石墨矿石为研究对象,综合运用石墨化学分析方法、单轴压缩试验和岩石统计损伤理论,研究不同固定碳含量石墨矿石力学性质差异,并试图建立考虑固定碳含量影响的石墨矿石单轴压缩荷载作用下的损伤本构模型。

1 石墨矿石固定碳含量测定与细观结构特征

固定碳含量是评价石墨矿石品质好坏的重要指标,固定碳含量越高,石墨鳞片尺寸越大、数量越多,其经济价值也越高[12]。本文的试验矿样取自黑龙江萝北云山石墨矿,取样岩石主要为石墨片岩。矿石中的固定碳含量主要集中于3%～20%之间,脉石矿物由30%～50%石英,30%～45%长石,5%～10%云母和少量金属硫化物等组成,矿石中石墨呈晶质鳞片状,片径一般为0.1～1.3 mm,最大可达2 mm。不同固定碳含量石墨矿石矿物种类基本相同,随着固定碳含量增加,石墨矿石逐渐由灰白色向灰黑色转变,其相应伴生矿物含量也逐渐减少。

图1 为试验所取矿石原样,从每块矿石原样上随机钻取小块样,破碎研磨成粉后混合均匀,测定其固定碳含量。固定碳含量的测定参照《JC/T 2572—2020 石墨矿固定碳含量测定方法》进行[13]。固定碳含量的测定由黑龙江萝北云山石墨矿石墨化学分析试验室完成,具体实施过程如图2 所示。固定碳含量用质量分数ω(CGD)表示,按式(1)～ 式(3)[13]计算。

图1 石墨矿石原样Fig.1 Raw graphite ore

图2 石墨矿石ω(CGD)测定流程Fig.2 Determination process of ω(CGD)

式中,ω(CGD)为固定碳含量;ω(V)为挥发分含量;ω(A)为灰分含量;ms为试料质量;m1、m4为空坩埚质量;m2、m3为残渣加坩埚质量。式中质量单位均为g;m1、m2由第一次灼烧后测得,m3、m4由第二次灼烧后测得。

图3 为石墨矿石偏光显微镜观测图,从图中可看出,石墨主要为鳞片状,和云母平行连生,局部有穿插关系,嵌布于脉石矿物颗粒之间。文献[7]指出,页岩中的鳞片状黏土矿物片理中存在不规则的碎屑颗粒和自生矿物,会降低软弱面的抗压和抗拉强度。类似地,石墨鳞片这种特殊结构,嵌布于石英、长石等矿物颗粒间,会形成细观尺度上的弱面结构,从而使石墨矿石力学强度发生弱化。此外,随着石墨矿石ω(CGD)的变化,其伴生矿物含量随之变化,而长石、石英等矿物,其强度一般高于石墨,所以,坚硬矿物含量和软弱矿物含量的变化,也会使石墨矿石的力学性能发生变化。

图3 石墨矿石偏光显微镜观测图Fig.3 Polarizing microscope view of graphite ore

2 石墨矿石单轴压缩试验及结果分析

2.1 试验概况

确定矿石原样的ω(CGD)之后,参照岩石物理力学性质试验规程[14]中关于岩石单轴抗压强度试验的建议,将矿块加工成ϕ50 mm×100 mm 的标准试样。为尽量减小试验离散性的影响,每种ω(CGD)的石墨矿石试样取自同一块矿石原样,挑选波速差别较小,孔洞、节理、缺口和裂纹等岩石缺陷不发育的试样开展单轴压缩试验。本次试验选用ω(CGD)为1.57%、5.19%、10.79%、12.65%和19.50%的5 组试样开展单轴压缩试验,每组准备5 个试样开展平行试验,选择其中离散性较小的3 个试样分析试验结果。试验所用的部分试样如图4 所示。

图4 石墨矿石试样Fig.4 Graphite ore samples

采用TAJW-2000 微机控制电液伺服岩石试验机作为试验加载系统进行单轴压缩试验。试验加载系统主要由压力负荷系统、油压系统、数据采集与控制系统等组成。试验机轴向最大试验力为2 000 kN,有效测力范围为20～ 2 000 kN,测力分辨率为1/500 000,示值相对误差≤±1%。控制系统采用进口原装德国DOLI 全数字伺服控制器,该控制系统控制精度高、可靠性能强,可以实现试验力、变形和位移等多种方式的加载。本次试验采用变形控制方式进行加载,设置加载速率为0.02 mm/s,加载至试样破坏停止加载。试验加载系统如图5 所示。

图5 TAJW-2000 岩石力学试验机Fig.5 TAJW-2000 rock mechanics testing machine

2.2 试验结果分析

2.2.1 力学特性分析

通过单轴压缩试验,得到不同ω(CGD)石墨矿石的基本力学参数,如表1 所示。表1 中,σf为单轴抗压强度,εf为峰值应变,二者均由试样应力应变曲线峰值点处取得;E为弹性模量,取值为0.5σf附近近似直线段的斜率。采用曲线拟合方法,得到试样单轴抗压强度、弹性模量和峰值应变随ω(CGD)的变化规律,如图6 所示。

表1 单轴压缩力学参数Table 1 Mechanical parameters of uniaxial compression

综合对比石墨矿石单轴抗压强度、弹性模量和峰值应变与ω(CGD)的拟合关系,可以发现,石墨矿石的力学参数与ω(CGD)存在显著相关性(相关性系数R2均大于0.96)。但从拟合关系来看,石墨矿石强度参数和变形参数随ω(CGD)的变化趋势有所差异。

从σf随ω(CGD)的变化规律图6 (a)来看,σf随ω(CGD)增加以愈渐平缓的趋势逐渐降低,总体上呈负指数型函数降低趋势,这说明ω(CGD)的增加降低了石墨矿石抵抗外界荷载的能力,但降低的程度会随ω(CGD)的增加而逐渐减弱,可见ω(CGD)的增加对石墨矿石力学强度的弱化存在限度。结合上文对石墨矿石细观结构的分析结果可知,ω(CGD)含量的增加诱发了石墨矿石内部矿物组分及细观结构的改变:一方面,石墨矿石内部坚硬矿物和软弱矿物含量因ω(CGD)的增加而此消彼长;另一方面,由石墨鳞片形成的细观尺度上的弱面结构,会因ω(CGD)的增加而出现尺寸和数量上的扩增。因此,在二者共同影响下,σf随ω(CGD)增加而逐渐降低。

图6 试样力学参数随ω(CGD)变化规律Fig.6 Variation of mechanical parameters of samples with ω(CGD)

从E随ω(CGD)的变化规律图6 (b)来看,E随ω(CGD)增加总体上呈线性降低趋势,这说明ω(CGD)的增加降低了石墨矿石的抗变形能力。其中,ω(CGD)为1.57%时,E值在90.69～98.37 GPa 之间,接近于石英的弹性模量[15-16];ω(CGD)为5.19%时,E值在68.74～72.34 GPa 之间,接近于长石的弹性模量[15-16]。而随着ω(CGD)继续增加,E值持续降低,ω(CGD)为19.50%时,石墨矿石的E值已远低于石英和长石的弹性模量。这说明,石英、长石等矿物,其抗变形能力远大于石墨矿物,随ω(CGD)增加,抗变形能力较强的矿物含量逐渐降低,而抗变形能力较弱的矿物含量则逐渐增高。而且,结合文献[5]中的结论可知,和坚硬矿物含量变化相比,软弱矿物含量变化对岩石整体力学性能的影响更大。因此,E随ω(CGD)增加逐渐降低。

从εf随ω(CGD)的变化规律图6 (c)来看,εf随ω(CGD)增加逐渐增大,且增大速率逐渐提高,总体上呈指数型函数递增趋势。εf一般是对试样达到峰值应力时的极限变形程度的反映,是表述岩石弹塑性性质的客观指标之一。由εf和ω(CGD)的拟合关系可知,ω(CGD)越高,εf越大,即试样达到峰值应力时,发生的变形更大,这说明高ω(CGD)的石墨矿石,有较为明显的塑性特征。

结合σf和E随ω(CGD)的变化规律来看,虽然随着ω(CGD)的增加,石墨矿石抵抗外界荷载和抗变形能力均逐渐减小,但由于ω(CGD)增加时,石墨矿石的变形能力也逐渐增强,且其变形能力增强的速率更快。因此,当外界荷载一定时,ω(CGD)较高的石墨矿石具有较强的塑性特征,能发生更大的变形,一定程度上延缓了石墨矿石的整体失稳破坏,从而使其强度随ω(CGD)增加而弱化的趋势有所减缓。

2.2.2 变形破坏特征分析

图7 给出了不同ω(CGD)石墨矿石试样典型的破坏特征图。结合试验室现象对其破坏特征进行分析,从破坏模式来看,C1.57%试样主要发生张拉破坏,试样破坏后的宏观裂纹较多。其中主裂纹由试样端部近似成直线向试样另一端部扩展,而试样端部则在轴向荷载作用下,产生杂乱的次生裂纹,主裂纹与次生裂纹聚合贯通,形成“Y”型破坏裂纹,导致试样整体失稳破坏,试样破坏时产生类似岩石崩坏的较大声响,并伴有碎块崩落。C5.19%试样主要发生拉剪混合破坏,破坏裂纹由试样端部沿2 条路径拓展,在临近试样另一端部时发生聚合,形成“V”型破坏裂纹,使试样发生整体破坏;试样破坏时伴有端部碎屑脱落,产生的声响次于C1.57%试样。C10.79%、C12.65%和C19.50%三种试样,均以剪切破坏为主,破坏裂纹由试样端部成一定角度向试样另一端部拓展、贯通,造成试样的整体性破坏。其中C10.79%和C12.65%两种试样,裂纹贯穿过程中会出现极少量的次生裂纹,但这些次生裂纹持续扩展的能力较差,并不能改变主裂纹的拓展路径,所以试样最终破坏时形成的破坏面较为单一和连续,对C19.50%试样来说,这一特征更为明显。三种试样破坏时均伴随低沉声响,破坏后的试样相对完整,说明其整体偏塑性破坏。ω(CGD)越高,试样塑性破坏越明显,这一现象与不同ω(CGD)石墨矿石试样力学特性呈现出的规律是一致的。

图7 试样破坏特征图Fig.7 Failure characteristic diagram of samples

进一步分析得到,ω(CGD)较低时,试样在外界荷载作用下,端部较为软弱的部位容易发生应力集中现象,导致试样端部出现细小、杂乱的裂纹,但此时试样岩石骨架并未失去承载能力。当主裂纹拓展贯通完成时,试样发生整体失稳破坏,而试样端部细小、杂乱的裂纹则因失去了岩石骨架的支撑和约束而快速发生崩坏和碎块脱落现象。ω(CGD)较高时,在外界荷载作用下,试样内部微裂纹开始孕育和拓展,由于高ω(CGD)试样内部石墨鳞片尺寸较大、数量也较多,容易形成较为连续的弱面结构,诱导裂纹拓展和贯通。因此,高ω(CGD)石墨矿石试样发生破坏时,主要沿着较为单一和连续的破坏面整体开裂,而较少出现局部崩坏和碎块脱落现象。

3 石墨矿石静态损伤本构关系

3.1 损伤变量的定义

根据上述分析,石墨矿石力学强度的弱化与石墨矿石ω(CGD)的增加存在显著相关性,而且由石墨鳞片形成的岩石内部弱面结构在加载之前就已经存在。因此,可将其视作岩石内部的初始损伤的一部分,并在建立其损伤本构关系时加以考虑。

根据文献[17]的研究成果,结合宏观唯象统计损伤力学理论可知,材料内部的劣化程度可用岩石的宏观力学性能响应表征。此处选用弹性模量度量石墨矿石的初始损伤,定义石墨矿石的初始损伤变量:

式中,EC为不同ω(CGD)石墨矿石的弹性模量;E0为ω(CGD)为0 时岩石的弹性模量。

同时,由于岩石材料内部还存在着大量诸如微孔洞、微裂纹等随机分布的原生缺陷,这些缺陷的存在使得构成岩石的微元在形状和强度上存在着很大差异[18]。受到外界荷载时,岩石微元将表现出不同的响应特性。假定岩石微元强度服从Weibull 分布,其概率密度函数可表示为

式中,P(x)为分布函数;x为分布变量;m、F0为分布参数。

岩石受到外界荷载时的损伤变量记为DS,DS与微元破坏的概率密度之间存在如下关系:

假定岩石微元的初始损伤为0,破坏时损伤为1,岩石微元破坏时的强度分布变量为F,则有:

对于不同ω(CGD)的石墨矿石来说,受荷过程中由ω(CGD)变化带来的损伤和受荷损伤相互影响,总损伤效应可等效为2 种损伤状态的耦合,记为DT,则有:

3.2 本构模型的建立

根据J.Lemaitre 应变等价性假说[19],可建立单轴压缩条件下岩石损伤的本构关系如下:

式中,σ为名义应力;EC为弹性模量;ε为应变;F是微元体强度分布变量,F可以是应力,也可以是应变,采用不同的破坏准则,其取值也会不同[20]。根据应变破坏准则[18],采用应变作为分布变量,则式(10)可表示为

式(11)即为不同ω(CGD)石墨矿石单轴压缩荷载作用下的损伤本构模型,其中EC、m和F03 个参数的表达式可通过试验数据确定。

3.3 参数求解

石墨矿石单轴压缩应力应变曲线峰值点处满足如下关系:

式中,εf为峰值应变;σf为峰值应力。

即:

进一步可得:

将表1 的试验数据代入式(15)和式(16),可计算得到参数m和F0的值,如表2 所示。

表2 分布参数计算结果Table 2 Distribution parameter calculation results

采用曲线拟合方法,得到EC、m、F0与ω(CGD)的关系,分别如图6(b)、图8 和图9 所示,拟合关系如式(17)～ 式(19)所示。

图8 参数m 随固定碳含量ω(CGD)变化规律Fig.8 Variation law of paramenter m with fixed carbon content ω(CGD)

图9 参数F0 随固定碳含量ω(CGD)变化规律Fig.9 Variation law of paramenter F0 with fixed carbon content ω(CGD)

将式(17)～式(19)代入式(11),得到不同固定碳含量石墨矿石单轴压缩荷载作用下的损伤本构模型,如式(20)所示。

式(20)即为考虑ω(CGD)影响的石墨矿石静态损伤本构模型,该模型只需知道具体的ω(CGD),便可计算出单轴压缩荷载作用下石墨矿石基本力学参数指标的具体数值。

3.4 模型验证

由式(20) 所给的损伤本构模型,得到不同ω(CGD)石墨矿石应力应变曲线。将理论曲线与试验曲线进行对比,如图10 所示。由图10 可看出,理论曲线与试验曲线吻合较好,理论曲线能较好地反映石墨矿石单轴抗压强度、弹性模量和峰值应变随ω(CGD)的变化规律,验证了模型的有效性与合理性。

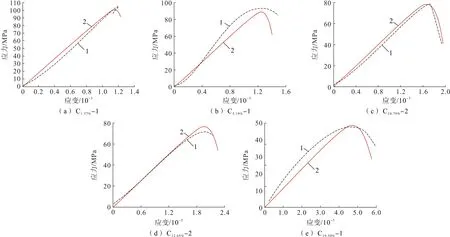
图10 理论曲线与试验曲线对比Fig.10 Comparison of theoretical curves and experimental curves

4 结论

(1) 固定碳含量增加导致石墨矿石内部硬质矿物和软弱矿物含量此消彼长,伴随石墨鳞片尺寸增大和数量扩增,石墨矿石力学强度随固定碳含量增加而弱化。

(2) 随固定碳含量增加,石墨矿石单轴抗压强度呈负指数型函数降低趋势、弹性模量呈线性函数降低趋势、峰值应变呈指数性函数递增趋势。

(3) 固定碳含量对石墨矿石单轴压缩荷载作用下的破坏模式有所影响,随固定碳含量增加,石墨矿石试样破坏模式由张拉破坏过渡到拉剪混合破坏,最后向剪切破坏转变。

(4) 引入与固定碳含量相关的损伤因子,建立反映固定碳含量影响的石墨矿石静态损伤本构模型,通过与试验曲线对比,验证了模型的有效性与合理性。