多场耦合条件下充填料浆管输壁面滑移特性

甘德清 薛振林 闫泽鹏 张友志 刘志义

(1.华北理工大学矿业工程学院,河北 唐山 063200;2.河北省矿业开发与安全技术重点实验室,河北 唐山 063009)

充填采矿法可以有效地控制地压、减少废料,达到建设绿色、安全矿山的目的[1]。近年来充填釆矿法在矿山的应用比重不断增加,其工艺技术也得到了迅猛发展,出现了水砂充填、分级尾砂充填、高浓度全尾砂充填和膏体充填等多种工艺手段[2]。与其他充填工艺相比,以采用高浓度全尾砂浆进行充填具有成本低、易于实现机械化的优点[3],管道输送是高浓度全尾砂充填工艺的关键环节,是确保系统稳定、高效运行的前提[4]。

高浓度全尾砂料浆是一种典型的非牛顿体[5],其在管道输送过程中会发生表观滑移现象,即由于高分子的迁移使得管壁附近料浆浓度变化,形成一层浓度较低(正滑移)或较高(负滑移)的滑移层,使得管壁附近料浆发生相对运动[6]。吴爱祥等[7]建立了考虑壁面滑移效应的膏体管道输送阻力模型,通过自制的倾斜管道试验装置,得到了膏体的流变学参数。Chen 等[8]通过流动实验结合穆尼分析法得出,不锈钢内壁的表面粗糙度最小时,聚合物的滑移速度达到最大。Hatzikiriakos S G 等[9]发现,当料浆的浓度较低时,固体颗粒不能有效地填充壁面附近区域,会形成一层几乎无颗粒的滑移层。Aral B K 等[10]通过试验证明,在给定剪切应力值的情况下,试验浆体温度为90 ℃时的滑移速度比25 ℃大2 个数量级。受到测量手段和试验装置的限制,对于管道输送过程中滑移现象的测量仅停留在理论上的计算和流量压力等变量的测量,不能直接地观察到管内的流动状况,粗略的测量值很难作为论证依据[11],传统两相流浆体与高浓度料浆结构流的输送差异性无法体现[12],如何精准地描述高浓度料浆在管道中的运移形态和变化规律是管道输送中存在的重大难题[13]。

随着计算机技术的发展,数值模拟成为研究流体流动的重要手段。谢翠丽等[14]采用了CFD 技术进行了“固壁静止”三壁滑移的数值模拟,表明壁面滑移速度对流场会产生一定影响。唐俊等[15]建立了关于熔体的壁面滑移模型,得出壁面滑移可以有效地减小其动阻力。刘赵淼等[16]采用CFD 分析微米级油膜缝隙流动情况下壁面滑移的规律,得出温度对壁面滑移具有促进的作用。Zhu L 等[17]通过格子Boltzmann 方法模拟微尺度通道内流体的滑移现象,揭示了该微尺度通道内的表观滑移机理,得出有效的滑动速度约为9%的主流区速度。Alfeus Sunarso[18]通过数值模拟的手段对宏观和微观收缩通道中聚合物流动的滑移行为进行研究,发现滑移效应的变化取决于浆体的流变性质,同时还依赖于通道的尺寸。上述模拟研究大多集中在单一物理场内进行,与实际输送过程中的复杂情况存在偏差,且直接针对滑移速度的研究较少。

基于前述分析,本研究建立考虑温度场、水化反应化学场及料浆管流流场的多场耦合滑移流动模型,通过Comsol 软件进行模拟计算,分析初始温度、料浆浓度及管径对滑移速度的影响规律,揭示高浓度料浆管道输送过程中的滑移机理,为料浆管道输送理论的完善提供基础依据。

1 数学模型

1.1 考虑滑移效应的基本流动方程

本次试验研究对象为高浓度充填料浆,其在管内发生的滑移属于表观滑移的范畴,壁面边界会形成一层粘度极低的薄层,使得管内流量较无滑移时增加,此时滑移流动的基本方程[20]为

式中,4ν/R为总流剪切速率;4νslip/R为滑移剪切速率;右边最后一项为主流区剪切速率。

1.2 水化方程

为了描述管道输送过程中水泥水化反应的程度,引入了式(2)来表示水泥水化反应与时间的二维映射关系。

式中,α(t)为t时刻水泥水化反应的程度;ωTr为料浆温度为Tr时的时间参数;ωS为水泥水化程度;参数α(f)为水泥水化的最终程度;λ为水与水泥的比值。最终水泥水化程度α(f)表示的为水泥水化反应的量与总水泥量的比值,所以α(f)的值不能超过1。计算得出,当λ为6.258 时,α(f)等于1。当λ<6.258 时,该等式在数学上是有效的,并且可以计算出相应的α(f)值;当λ>6.258 时,等式无效,在这种情况下α(f)的值被认为是1。

1.3 热传递方程

高浓度料浆在管道输送过程中的水化反应热、热量传递之间的耦合关系,可以通过comsol 软件的内置数学模型来表述:

式中,(ρC)eq是充填料浆等效的体积热容量;ρw为充填料浆的密度;Cw为常压下充填料浆的热容;keq为充填料浆的热传导系数;uw为充填料浆的速度场;Q为热源项(水泥水化放热)。

水泥水化的产热率Qc(t)可以通过以下表达式来计算:

式中,Hc为水泥水化产生的热量;Tr为参考温度;Tc是料浆的温度;ωTc和ωTr为水泥水化在相应温度的时间参数;ETc为表观活化能,当Tc高于或等于20 ℃时,其为恒定值(33 500 J/mol);Tc低于20 ℃时,其值随Tc变化,可采用式(5)计算。

1.4 控制方程

在流体力学中,主要的流动参变量有:流体压力p、密度ρ、温度T和流速u、ν、w。对于不可压缩流体,comsol 软件中控制流动传热的基本方程主要有能量守恒、动量方程、质量方程和状态方程[21]。

Navier-Stokes 动量守恒方程(忽略外部体积力):

传热(能量守恒)方程(在傅里叶导热定律与能 量守恒定律的基础上添加剪切应力得到):

质量守恒方程:

状态方程:

2 数值模型可靠性验证

为了对本次实验设计多场耦合模型的有效性进行检验,本节内容引用刘晓辉[22]等的实验结果,其研究重点为在壁面滑移作用下管内的输送阻力。根据他们数据记录管段的尺寸,设计几何模型为内径150 mm、长26 m 的圆柱形直管。为了减少计算时间几何模型基于二维轴对称空间维度进行构建(通过对某一切面流场的计算进而反演整个管道中的流动状态),几何模型如图1 所示,阴影部分为实际计算区域。

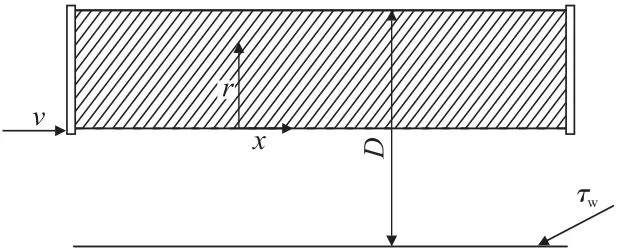
图1 几何模型示意Fig.1 Schematic diagram of geometric model

2.1 结果合理性分析

数值模拟计算必须收敛才能得到有效的运算结果[23]。采用Comsol 进行计算时生成收敛曲线,如图2 所示。图中“步长倒数”指的是单位时间内求解器的计算次数,其与计算时发生的误差呈正相关。当某时段计算不奇异时,瞬态求解器会增加在该时段内计算的次数,也就是减小计算步长(增大步长倒数)。图2 表明模型在前期计算过程中步长倒数增大运算频率升高,但是随着运算的持续进行,曲线总体上呈减小的趋势,计算过程中的不奇异次数在逐渐地减小。经过60～80 次时间步的迭代后最终都趋于稳定,该曲线证明了本次模拟运算得出的结果是合理有效的。

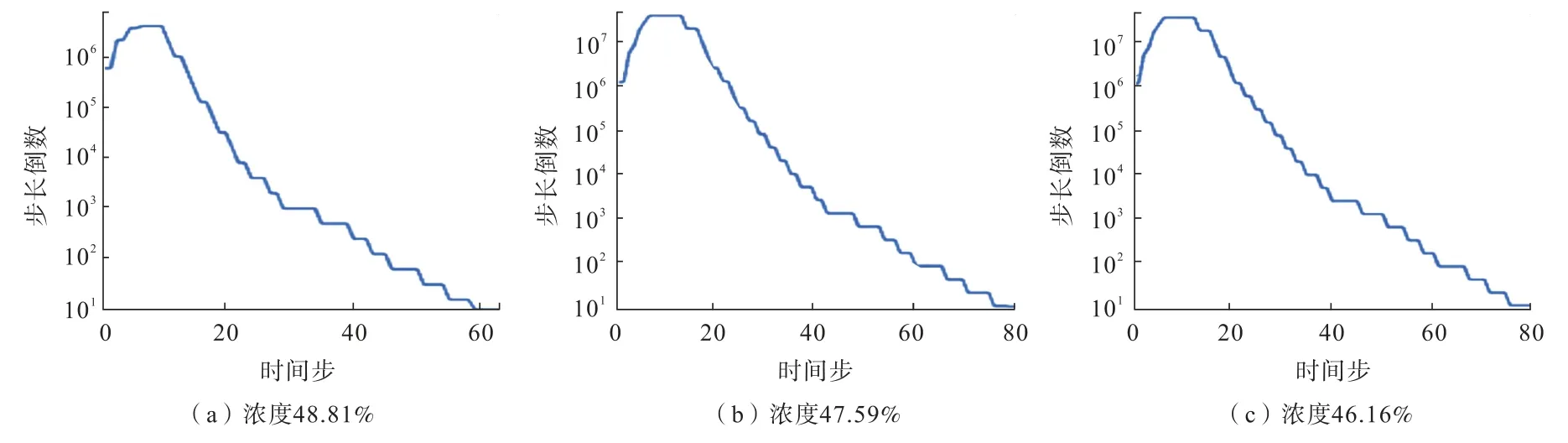
图2 瞬态求解器收敛图Fig.2 Transient solver convergence graph

2.2 模型有效性分析

根据相关文献中的参数进行模拟实验,参数如表1 所示。将数值模拟的结果与刘晓辉[22]的实测结果进行比较,见图3。

表1 模型验证参数Table 1 Model verification parameters

图3 表明数值模拟结果与实测数据误差在10%以内,由于实测数据是考虑壁面滑移效应管道的输送阻力,说明多场耦合数值模型是可靠的,利用该模型分析得出的壁面滑移速度变化规律是合理的。

图3 模型计算结果Fig.3 Model calculation result

3 壁面滑移速度规律分析

为了对壁面滑移的规律进行针对性的分析,减少其他因素对研究结果的影响,几何模型设定为4 m 长的圆柱形管,通过数值模拟来分析初始温度、管径及浓度对壁面滑移速度的影响规律,试验方案见表2。

表2 数值模拟参数Table 1 Numerical simulation parameters

3.1 壁面滑移速度的提取

图4 为考虑壁面滑移效应的管内速度分布情况。由图4(a)可以看出,当料浆以1.5 m/s 的速度进入管道后,受到壁面剪切的作用,使得中部塞流区面积减小但是颜色逐渐加深,产生了较大的速度梯度,当经过一段时间的输送后管内料浆的流动状态趋于稳定;图4(b)为沿管道走向均匀分布的6 条管道径向速度分布图,可以明显地看出管道内料浆塞流区域减小其对应的速度不断增大,最大速度达到1.82 m/s,模型边界处浆体流动速度不为0,其值在0.22 m/s左右。

图4 管道内流速分布Fig.4 Flow velocity distribution in pipeline

由于高浓度料浆在流动过程中在管壁处形成的滑移流动层厚度极薄(一般小于10 μm)。为了对滑移层速度进行针对性分析,作一维曲线图,以“定义截线”的方法选取几何模型表层沿管道走向的速度数据见图5。

由图5 可以看出,高浓度料浆原来的初始速度为1.5 m/s 进入管道后急速下降为0.217 m/s 此时输送距离为0.22 m,随后滑移速度稳定在0.19～0.22 m/s,我们称这个转折点为管内输送结构开始稳定的“触变平衡点”。本次对壁面滑移速度的研究主要是选取“触变平衡点”后方区域(见图5),通过数据查询手段得到其平均值,以表征在该条件下的壁面滑移速度(νslip)。

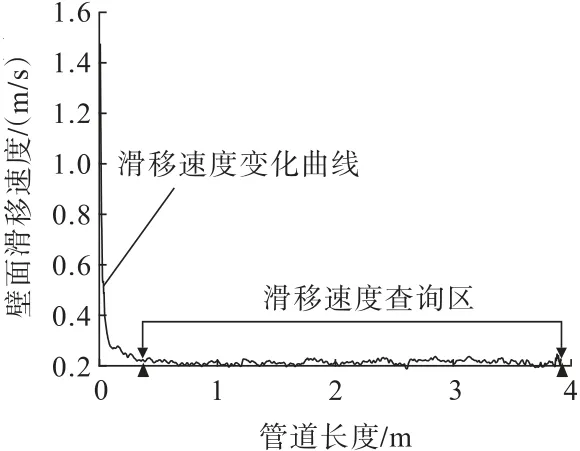
图5 管道壁面附近浆体流动速度Fig.5 Slurry flow velocity near the wall of the pipe

3.2 温度对滑移速度的影响规律

图6(a)为温度对壁面滑移速度的影响规律,不同温度条件下,均产生了明显的滑移速度。温度对滑移速度产生了较大的影响,随着温度的增大,壁面滑移速度呈增长的趋势,且增长速率越来越小。图6(b)为受水化反应和摩擦生热(通过添加边界热源实现)影响时,管道2 m 处浆体温度的增量。20 ℃时壁面附近的温度增量为0.11 ℃,随着初始温度的增大,极大地促进水泥水化反应,增加了水化放热量,初始温度70 ℃时,温度增量达到最大值0.32 ℃。

图6 温度对壁面滑移速度的影响Fig.6 Effect of temperature on wall slip speed

高浓度料浆中的颗粒在管道输送过程中受到多种作用力的影响,“范德华力”是影响颗粒间黏附强度的主要因素,其属于近程力且对颗粒的接触后行为起主导作用。由于“范德华力”的作用,高浓度料浆中存在着大量的“絮网”结构,温度升高会加剧料浆内部颗粒的布朗运动,使得颗粒挣脱“范德华力”的束缚,破坏“絮网”结构,并促使其向黏性较低的“液网”结构转化[24]。温度越高,浆体的水化反应越充分,水化放热量越大,同时受到摩擦生热的影响,导致70℃时壁面附近浆体的温度增量达到最大值,结合前述分析得出,此时壁面附近浆体黏度与温度呈反比例关系,70 ℃时滑移层黏度与主流区黏度的差值最大,此时滑移速度达到最大值。同时浆体内部的“絮网”数目是一定的,“絮网”向“液网”间的转换并不是无限制的,当超过一定温度时其转换效率降低,滑移速度的增长率减小。

3.3 管径对滑移速度的影响规律

图7 为管径对滑移速度的影响规律。由图7(a)可以看出,滑移速度(νslip)在管径为60 mm 时达到最大值0.213 m/s,此后随着管径的增大,νslip开始缓慢地下降。当管径增大到180 mm 时,发现壁面附近的速度曲线断断续续,如图7(b)所示,说明此时管道内部不存在完整的滑移过程,认为其不存在滑移速度(νslip=0);管径为200 mm 时,现象相同。

图7 管道内径对滑移速度的影响Fig.7 Influence of inner diameter of pipe on slip speed

管径变化时引起管道两端输送阻力(Δp)的变化,壁面剪切作用力与Δp及管径存在如下关系:

式中,Δp为管道输送阻力,Pa;L为监测管段长度,m;R为管道半径,m。将模拟实验所测得数据,代入式(12)中,发现随着管径的增大,剪切应力呈反比例函数的趋势下降,如图8 所示。

图8 管道内径与剪切作用力的关系Fig.8 Relationship between inner diameter of pipe and shearing force

管径的改变引起管道内部浆体所受剪切作用力的变化,导致料浆内部颗粒发生迁移,从而使得边界层性质发生改变,影响壁面滑移速度。在实验过程中,发现存在临界剪切应力值,当浆体所受剪切作用力超过临界剪切应力时才会出现滑移现象,且随着剪切作用力的持续增加,呈增大的趋势。管道内尾砂颗粒受力情况如图9 所示。

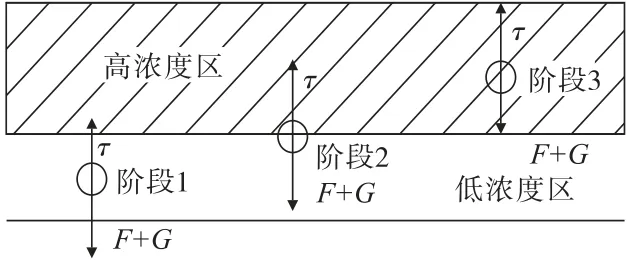
图9 浆体内部尾砂颗粒受力情况Fig.9 The force of the tail sand particles inside the slurry

将尾砂颗粒的受力情况分为3 个阶段:阶段1(τ﹤F+G)、阶段2(τ=F+G,临界值),对应管径为180～200 mm 时的模拟条件,此过程内尾砂颗粒所受剪切作用力较小,不能够克服其受到的阻力向中部高浓度区域迁移,壁面附近浆体与主流区浆体密度相差很小,可能会在局部区域产生滑移速度,但是不存在完整的滑移过程;阶段3(τ>F+G),对应管径为60～170 mm 时的模拟条件,此时壁面剪切作用力大于其所受阻力,颗粒迁移运动距离、边界层浓度远小于主流区,出现明显的滑移现象,且νslip与边界层厚度及剪切应力呈正相关。

3.4 料浆浓度对滑移速度的影响规律

浓度是影响高浓度料浆流变特性的关键性因素,本节内容通过改变料浆初始速度来获得不同浓度情况下料浆滑移速度的变化规律。为了方便分析我们将所测得的Δp通过式(12)转化为剪切作用力,作表观滑移速度随剪切作用力变化的曲线,发现其与陈良勇等[25](管流法)与曹琪等[26](PIV 技术)所得壁面滑移速度的规律具有高度的一致性,如图10 所示。

由图10 可以看出,浆浓度为70%时,νslip数值最大、曲线较为平缓,料浆所受剪切作用力达到44 Pa出现壁面滑移现象,νslip为0.206 m/s;当τ值为83 Pa 时,νslip达到最大0.257 m/s。料浆浓度为65%时,料浆所受剪切作用力达到38 Pa 出现壁面滑移现象,νslip为0.135 m/s;当τ值达到82 Pa 时,νslip达到最大0.233 m/s。料浆浓度为60%时,τ值达到35 Pa出现滑移现象,νslip为0.085 m/s,νslip与剪切作用力成正相关,但曲线斜率大于上述2 条曲线;当τ值为80 Pa 时,νslip达到最大值0.214 m/s。

图10 浆体浓度对壁面滑移速度的影响Fig.10 Effect of slurry concentration on wall slip velocity

经分析,料浆浓度较高时,发生滑移的动力来源主要是“动态壁面损耗效应”[27],即滑移层的形成主要由剪切力引导的尾砂颗粒的迁移运动所控制。颗粒在迁移的过程中还受到渗透压及自身重力的影响,浆体浓度越高,渗透压越大,浆体发生壁面滑移所需的临界剪切作用力越大;随着壁面剪切应力的持续增加,滑移层厚度变大,壁面滑移速度呈增长的趋势。由于浆体浓度较高时固体颗粒所受到的剪切作用力较大,因此当其达到临界剪切作用力后,浓度较高的浆体所形成的滑移层较厚,壁面滑移速度较大。

4 结论

本文对温度场、水化反应化学场及料浆管流流场耦合作用下高浓度料浆的壁面滑移行为进行了研究,并得到了料浆浓度、温度及管径对壁面滑移速度的影响规律,主要结论如下:

(1)壁面滑移速度随温度的增加而增大。温度升高会加剧料浆内部颗粒的布朗运动,使得部分尾砂颗粒挣脱“范德华力”的束缚,促使“絮网”结构向着“液网”结构转换,浆体黏度变小,滑移速度增大。

(2)管径增大时,壁面滑移速度缓慢减小。管径增大,浆体所受剪切作用力减小,颗粒迁移运动减缓,滑移速度降低;管径增大至180 mm 时,剪切作用力小于临界值,管内不存在完整的滑移过程。

(3)浓度增大,浆体发生滑移运动时所需的临界剪切应力增大。料浆浓度较高时,发生滑移的动力来源主要是“动态壁面损耗效应”,固体颗粒需要克服渗透压及自身重力的作用发生迁移运动,而渗透压主要与浆体浓度有关,且与浆体浓度呈正相关,因此浓度增加时,固体颗粒需要克服的阻力增大。