基于决策树的地下工程透水事故发生风险定量评估

刘建坡 徐孝男 武 峰 李烽田 王永昕

(深部金属矿山安全开采教育部重点实验室,辽宁 沈阳 110819)

随着经济持续高速发展,我国地下工程(矿山、地下隧道工程、水电工程等)建设速度居于世界前列,其工程类型众多且建设深度和规模不断增大。在这种背景下,地下工程水文地质特征愈加复杂,透水事故频发,例如,2019 年5 月17 日黑河翠宏山铁多金属矿发生特大突水事故,采空区塌陷引起地表滨河水库大量水携泥沙溃入井下,致使43 人被困8 人失踪;2019 年12 月14 日四川宜宾杉木树煤矿发生重大透水事故,越界开采导致相邻煤矿老空区积水瞬间冲破边界煤柱涌入矿井,5 名作业人员当场死亡;2021 年7 月15 日珠海石景山隧道右洞施工工程中发生特大突水事故,瞬时最大涌水量达到7 200 m3/h,水流带出淤泥堆积数米,造成14 人死亡。各类透水灾害造成了严重的人员伤亡和重大经济损失,严重制约地下工程的安全建设作业。开展透水灾害发生风险定量评估研究,对于透水灾害救灾决策制定具有重要意义。

针对地下工程透水事故的致灾因素及风险预测评估,国内外专家学者展开了大量研究。Bukowski[1]考虑了水压、涌水悬浮物含量、围岩和矿柱稳定性以及井筒历史突水情况几个因素,提出了一种突水灾害发生风险评估系统。李利平等[2]开发了包含不良地质、超前地质监测信息等8 个风险评价因素的软件系统用于突水灾害发生风险实时评价。李术才等[3]通过收集岩溶隧道典型突水突泥事故案例,分析相关致灾因素,建立了突水突泥风险评价指标体系并对齐岳山隧道突水突泥风险进行了评估工作。陈歌等[4]引入微震监测技术开展矿井水害防治和预测预报研究并系统分析了突水灾害煤岩体微震活动性前兆规律。李文平等[5]针对煤矿底板奥灰水害问题,收集了大量突水案例数据,建立了地下突水灾害风险评估方法,并将突水风险分为安全、中等安全、潜在风险和高风险4 个等级。殷颖等[6]统计收集了160 个隧道突水突泥灾害案例,总结工程地质、自然环境和人为诱发因素对突水突泥灾害发生频率的影响程度,分析并总结各因素对突水突泥的影响规律。邱梅等[7]对梁庄煤矿13 号煤层下伏奥灰含水层的突水风险性进行了预测评估。王迎超等[8]以鸡公岭隧道和峡口隧道2 个典型深埋岩溶隧道为背景,选取了地形地貌、层间裂隙等7 个指标用于突水风险预测评估。在以上研究中,采取的评估方法主要有基于风险指标判据的综合评价方法和基于机器学习的综合评价方法两类。其中,基于风险指标判据的综合评价方法包括模糊综合评价[8-9]、云模型[10-11]、属性数学理论[12-13]、层次分析法[14-15]、D-S 证据理论[16]等;基于机器学习的综合评价方法主要包括贝叶斯网络[17]、神经网络[18-19]、随机森林[20]、支持向量机[21]、万有引力法[22]等。决策树是一种基于“信息增益”的方式对样本进行分类的机器学习方法,因其模型简单直观且可解释性较好,得到了广泛应用。

以上研究中多以瞬时最大涌水量等指标定义灾害风险等级,而累计涌水量对于救灾决策也具有重要指导作用。因此,在透水灾害风险等级确定时,综合考虑瞬时最大涌水量和累计涌水量,可为救灾决策提供更为全面的指导。本文通过系统分析国内外107组典型地下工程透水事故案例,建立了透水事故发生风险评估数据库,基于瞬时最大涌水量和事故累计涌水量2 个指标,采用k均值聚类算法划分了案例库样本的灾害等级。在此基础上,选取水文条件、地层岩性和过程监测信息3 个方面共6 个指标,基于决策树方法建立了透水事故发生风险评估模型,为地下工程透水事故救灾决策提供理论和技术支撑。

1 透水灾害等级划分及评估方法

建立透水风险评估模型,首先需要进行统一标准的灾害等级划分。本文采用k均值聚类算法确定透水事故的灾害等级,并以此为基础,基于决策树方法建立透水事故发生风险评估模型。

1.1 k 均值聚类

k均值聚类是常用的基于样本划分的聚类算法,其基本思想是事先指定类别数k,采用迭代的方式不断更新聚类中心和划分并通过损失函数的最小化选取最优的划分。本文在应用该方法过程中,对于透水灾害案例数据集X的n个样本数据,每个样本由m个属性(例如:人员伤亡与经济损失、透水过程监测信息等)的特征向量组成,即X={x1,x2,…,xn}。

当透水灾害等级为k级时,可以将n个样本划分为k个子集C,C={C1,C2,…,Ck},采用k均值聚类方法的计算步骤如下:

(4)迭代优化。k均值算法使用误差平方和准则函数来评价聚类性能,最终聚类结果的误差平方和E的计算公式如下:

为求最小化平方误差,通常采用迭代的方法:重复步骤(2)和步骤(3),迭代t轮后若数据集X中各个样本所对应的灾害等级与第(t-1)轮迭代结果相同,则停止迭代,令:

式中,C(t)为第t次迭代得到的聚类结果。

1.2 决策树方法

决策树广泛应用于各种分类与回归问题。一般情况下,一棵决策树包含一个根结点、若干个内部结点和若干个叶结点,其中:根结点包含样本全集,叶结点对应于决策结果,其他每个结点则对应于一个属性测试,每个结点包含的样本集合根据属性测试的结果被划分到子结点中,根结点到叶结点的最长路径的长度称为树的深度。因此,该方法核心思想即通过逐层选择最优划分属性,将不同样本划分到相应类别中,最终生成一棵稳定性好、泛化能力强的决策树。

假设给定包含n个样本、共有k个灾害等级类别的透水灾害案例数据集S,每个样本由u个属性的特征向量组成,即S={(x1,y1),(x2,y2),…,(xn,yn)}。其中,X=(x1,x2,…,xn)为输入实例样本,yi∈{1,2,…,k}为灾害等级类别标记(i=1,2,…,n)。

决策树模型生成的计算步骤如下:

(1)计算数据集的信息熵。假定灾害数据集S中第i类灾害等级样本所占的比例为pi(i=1,2,…,k),则S的信息熵定义为

式中,Entropy(S)代表灾害数据集S的信息熵,单位为bit。

(2)计算每个属性对数据集的信息条件熵。对于S中某一属性A(例如水压、离子浓度等),属性A对S的信息条件熵计算式如下:

式中,Entropy(S|A)代表属性A对数据集S的信息条件熵,表示在A给定的条件下对S进行分类的不确定性;Sj代表某一特定灾害等级的样本集合;分别代表集合Sj和集合S的样本个数;Entropy(Sj)代表数据集Sj的信息熵,j=1,2,…,k。

(3)计算信息增益。

式中,Gain(S,A)代表属性A对数据集S的信息增益,表示属性A对数据集S进行分类的不确定性减少的程度。通常,采用最大信息增益的属性作为最优划分属性。

2 透水灾害等级划分及评估指标选取

2.1 透水灾害案例库及等级划分

本文统计了国内外91 个地下工程共107 起透水事故案例,通过分析灾害发生原因、类型及致灾因素,建立起了透水灾害案例样本数据库,其中金属矿、隧道工程、煤矿透水案例数量分别为16、39 和52,占比分别为15%、36.4%和48.5%。

本研究选取瞬时最大涌水量和累计涌水量2 个指标,依据传统透水灾害等级划分标准(特大型、大型、中型和小型4 级[14])确定聚类数目k=4,根据式(1)～式(4),得到4 个包含不同样本数的样本集合(类别1、类别2、类别3 和类别4)。为了更直观地看出每个类别实际代表的等级,以实际灾害等级为依据,对聚类结果进行了统计分析(图1、表1)。从图中可以看出,类别1、类别2、类别3 和类别4 分别包含18、25、38 和26 个样本数据,分别占比16.8%、23.4%、35.5%和24.3%。其中,类别1 包含14 个小型(占比77.8%)、3 个中型和1 个大型透水样本;类别2 中包含18 个中型(占比72.0%)、4 个小型和3个大型透水样本;类别3 中包含31 个大型(占比81.6%)、5 个特大型和2 个中型透水样本;类别4 中包含22 个特大型(占比84.6%)、3 个大型和1 个中型透水样本。根据聚类结果的4 个样本集合所含不同灾害等级样本的数目情况可以判断,类别1、类别2、类别3 和类别4 分别与小型、中型、大型和特大型灾害等级相对应。

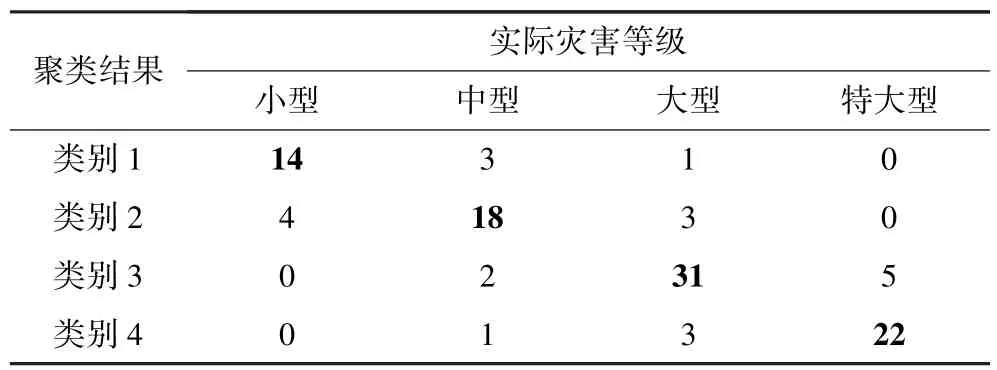
表1 样本聚类结果与实际灾害等级对比Table 1 Comparison between sample clustering results and actual water inrush level

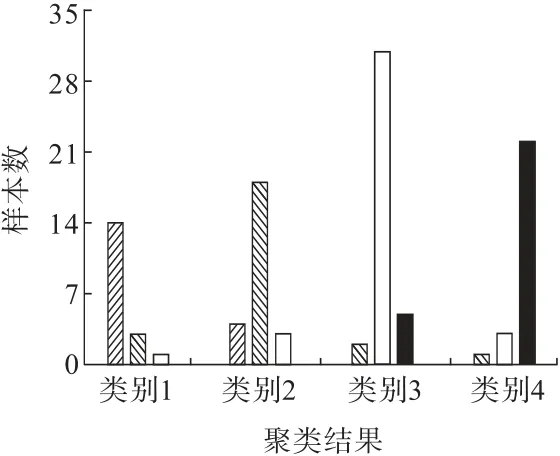
图1 聚类结果统计描述Fig.1 Statistical description of clustering results

2.2 透水事故发生风险评估指标

综合考虑透水样本指标数据的完整性以及指标与透水灾害等级相关性2 个条件,最终选取水文地质条件、岩性因素和透水过程指标三方面指标。其中水文地质条件包括水文条件加权值、地下水位高程差和工程埋深3 个指标;岩性因素为围岩饱和单轴抗压强度;透水过程指标包括涌水量平均增长速率和累积涌水量2 个指标,具体如下:

(1)水文条件加权值x1是主要含水层富水性(按钻孔单位涌水量)、水源补给能力(按负地形面积占比)、地下水连通性三者的加权值,可以综合反映该研究区域的水文情况,其中区域富水性分级标准见规程[23],文献[24]给出了水源补给能力和地下水连通性的分级评分标准。

(2)地下水位高程差x2表示地下水位面与基准面(巷道或隧道底板)的高程,是影响瞬时突水强度的重要因素之一[15]。

(3)随着工程埋深x3增大,地下水迳流活动、含水层水力联系等显现出逐渐增强的趋势[25],在这种情况下发生透水事故往往更容易造成较严重的后果。

(4)围岩岩石饱和单轴抗压强度x4可以在一定程度上反映巷(隧)道围岩的力学性质,是影响透水是否发生的一个重要因素[26]。

(5)典型突水灾害的涌水量时程曲线可分为两种类型(图2):第一种突水发生过程常伴随着涌水点数目增多、涌水通道扩张等现象,存在较为明显的灾变期,例如底板灰岩含水层承压突水、顶板砂岩裂隙突水等;第二种突水发生过程通常无显著前兆,往往是采掘过程不慎导通储水构造(老空区、岩溶溶腔等)造成的瞬时突水,若无其他层位的地下水补给,则表现为静储量疏干型。本研究中将两类突水灾害涌水量时程曲线划分为灾前稳定阶段、灾变阶段和成灾阶段3 个阶段,其中第二种突水类型没有进行灾变阶段的划分。图2 中,Qn、Qan、Qs和Qm分别代表稳定涌水量、异常涌水量、突增涌水量和初次最大涌水量,t1、t2和t3表示达到相应涌水量所对应的时间,涌水量平均增长速率x5可以通过图中公式求得,累积涌水量x6为相应时间区间下的面积S1和S2。

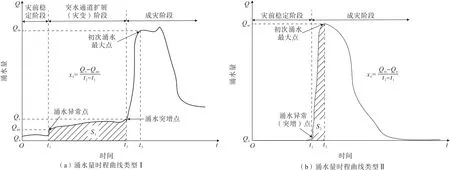
图2 两类突水灾害典型涌水量时程曲线示意Fig.2 Schematic of typical water inflow time-history curves of two types of water inrush hazard

指标的可靠性是影响透水事故发生风险评估准确性的重要因素。因此,在透水风险评估指标确定的基础上,统计不同灾害等级下样本各指标的平均值,并进行了归一化处理(图3)。从图3 可以看出,水文条件加权值、水位高程差、埋深、涌水量平均增长速率和累积涌水量5 个指标与灾害等级呈正相关,而岩石饱和单轴抗压强度与灾害等级呈负相关关系,这表明本研究中选取的指标均与透水灾害等级存在较强的相关性,可用于透水事故发生风险评估模型的建立。

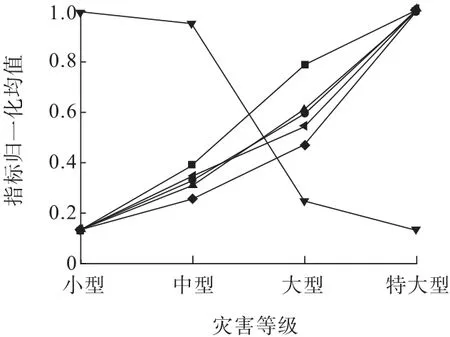
图3 指标归一化均值与灾害等级的关系Fig.3 The relationship between the normalized mean of the indicators and the water inrush level

3 透水事故发生风险评估

本研究将107 组透水事故样本按照样本数比7 ∶1 ∶2 划分为训练集、验证集和测试集(表2),即:75个样本作训练集建立决策树模型,11 个样本作验证集对生成的决策树进行剪枝优化,21 个样本作测试集对最终生成的剪枝决策树进行模型评估。表2 中,x1～x6代表各指标属性,y为灾害等级,其数值0、1、2、3 分别对应小型、中型、大型和特大型透水灾害等级。

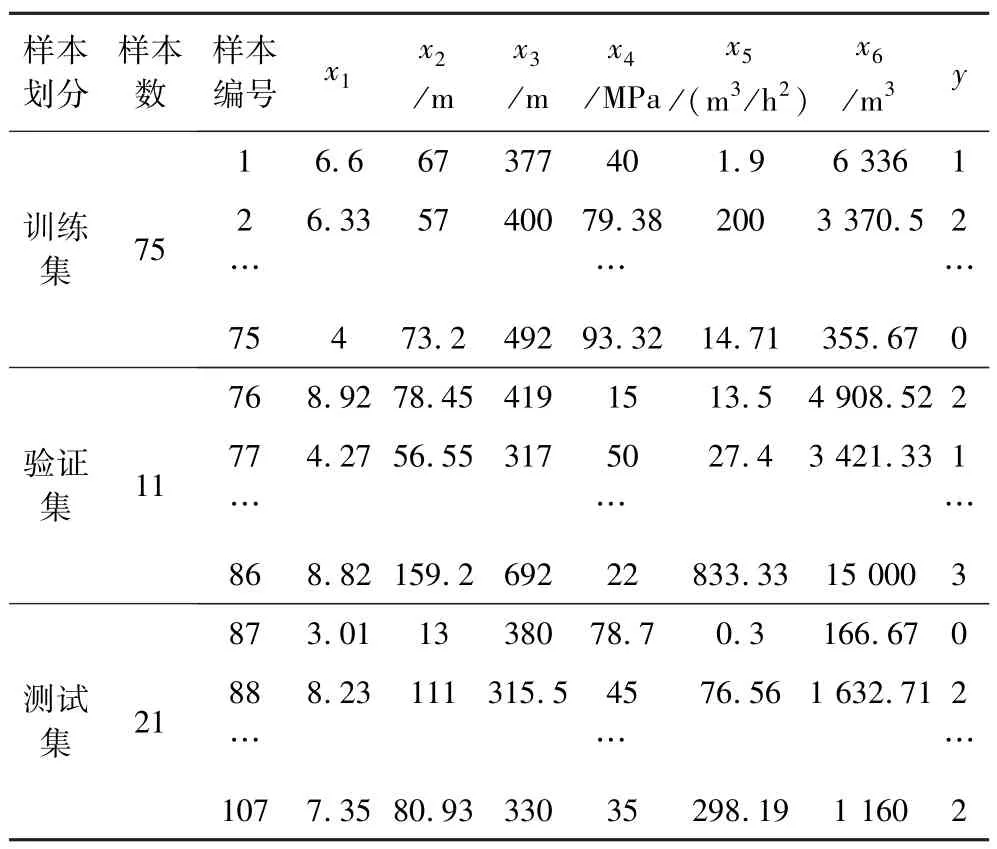
表2 透水灾害样本数据集的划分Table 2 The division of the water inrush sample data set

3.1 透水事故发生风险评估决策树模型

透水事故发生风险评估决策树模型的建立过程如下:首先,根据式(5)～式(7),可以获得训练集(视为树深度为0 的根结点)的信息熵值1.979,并依据信息熵值计算得到最优划分属性x1和划分结点值6.28;之后,以最优划分属性x1的值与划分结点值6.28 的相对大小为依据将训练集样本划分为2 个子集,共同构成树深度为2 的内部结点;再后,重复以上过程,计算2 个子集的最优划分属性和划分结点值,进而进一步分裂这2 个子集,直至决策树模型建立完成。在本研究中,训练集的决策树模型树深度为6(表3)。随着树深度的增加,内部结点的数目成倍递增,每个内部结点所含样本数逐层递减,样本划分越精细。若某一内部结点所含样本均为同一灾害等级,即该内部结点为叶结点,则停止继续划分,可直接给出该路径下的风险等级。

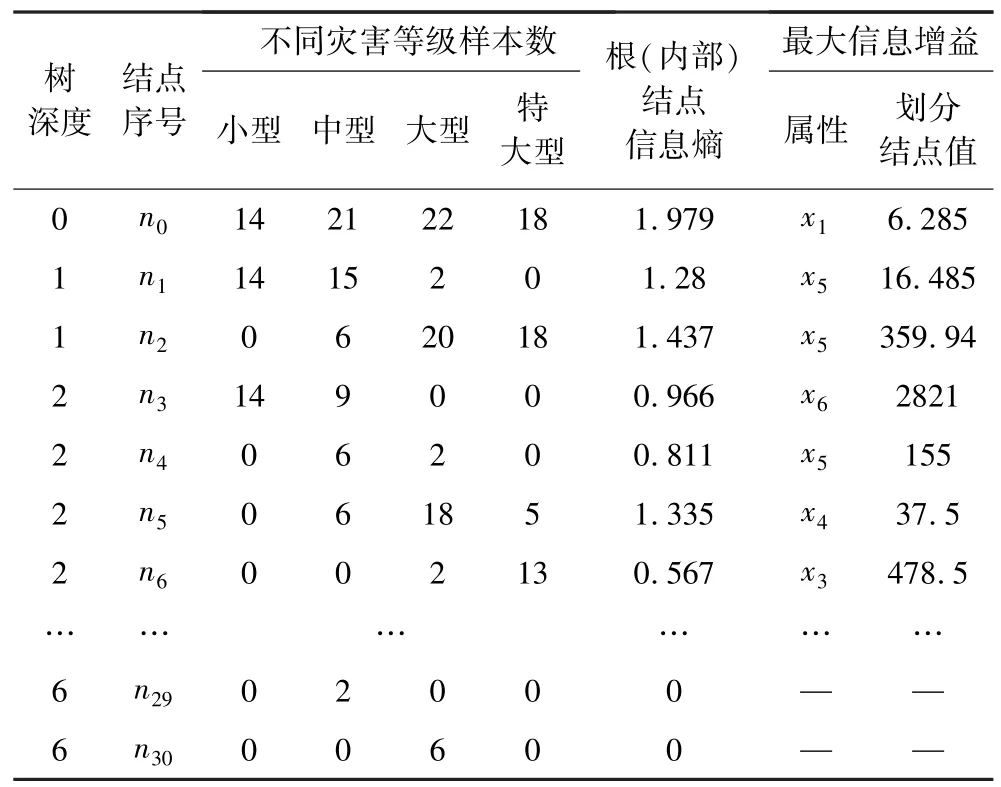
表3 决策树划分依据Table 3 Decision tree division basis

在上述决策树模型建立基础上,采用验证集样本进行了验证,准确率仅为63.6%,表明该模型泛化能力较差,不能满足透水事故发生风险评估的需要。造成该问题的主要原因是在模型建立过程中出现过拟合,图4 中训练集样本拟合精度随着最大叶结点数目的增多而增加(当最大叶结点为17 时,评估准确率达100%),但是验证集样本的评估准确率却在最大叶结点超过9 之后出现显著降低的现象。为解决该问题,本研究中采用剪枝方式对决策树模型进行了处理,避免出现过拟合现象。在决策树方法中,剪枝是防止生成的树过拟合、提高模型评估准确率的主要手段,其基本策略有“预剪枝”和“后剪枝”2 种:前者是在决策树生成过程中对结点属性进行划分时作判断,后者是生成决策树后自下而上地对非叶结点进行判断。后剪枝决策树往往比预剪枝决策树保留更多分支,避免过拟合的同时降低欠拟合风险。因此,本研究采用后剪枝策略,并以模型泛化性能是否提升作为剪枝标准,对模型进行了优化处理。以图5 中树深度为5 的结点n28为例,该结点包含8 个透水样本(6 个大型和2 个中型),尝试对其剪枝(替换为叶结点)并标记为“大型”灾害等级之后的验证集样本预测准确率并未提升(仍为63.6%),故仍保留此内部结点(保留n29和n30)。对于包含15 个透水样本(12 个大型和3 个特大型)的结点n11,尝试对其剪枝(替换为叶结点)并标记为“大型”灾害等级之后的验证集样本预测准确率显著提升(从63.6%提升至81.8%),故对其进行剪枝处理(剪掉n19,n20,n25和n26)。基于以上剪枝策略,建立了透水发生风险评估剪枝决策树模型。通过针对验证集样本进行评估,准确率提高至90.9%。

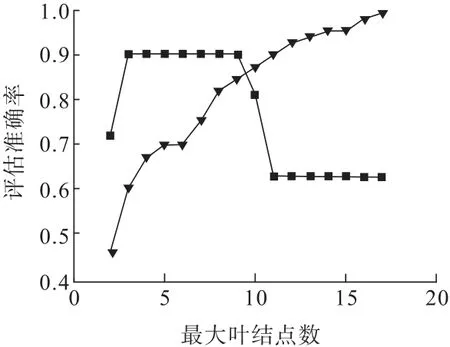
图4 最大叶结点数检验曲线Fig.4 Test curve for maximum number of leaf nodes

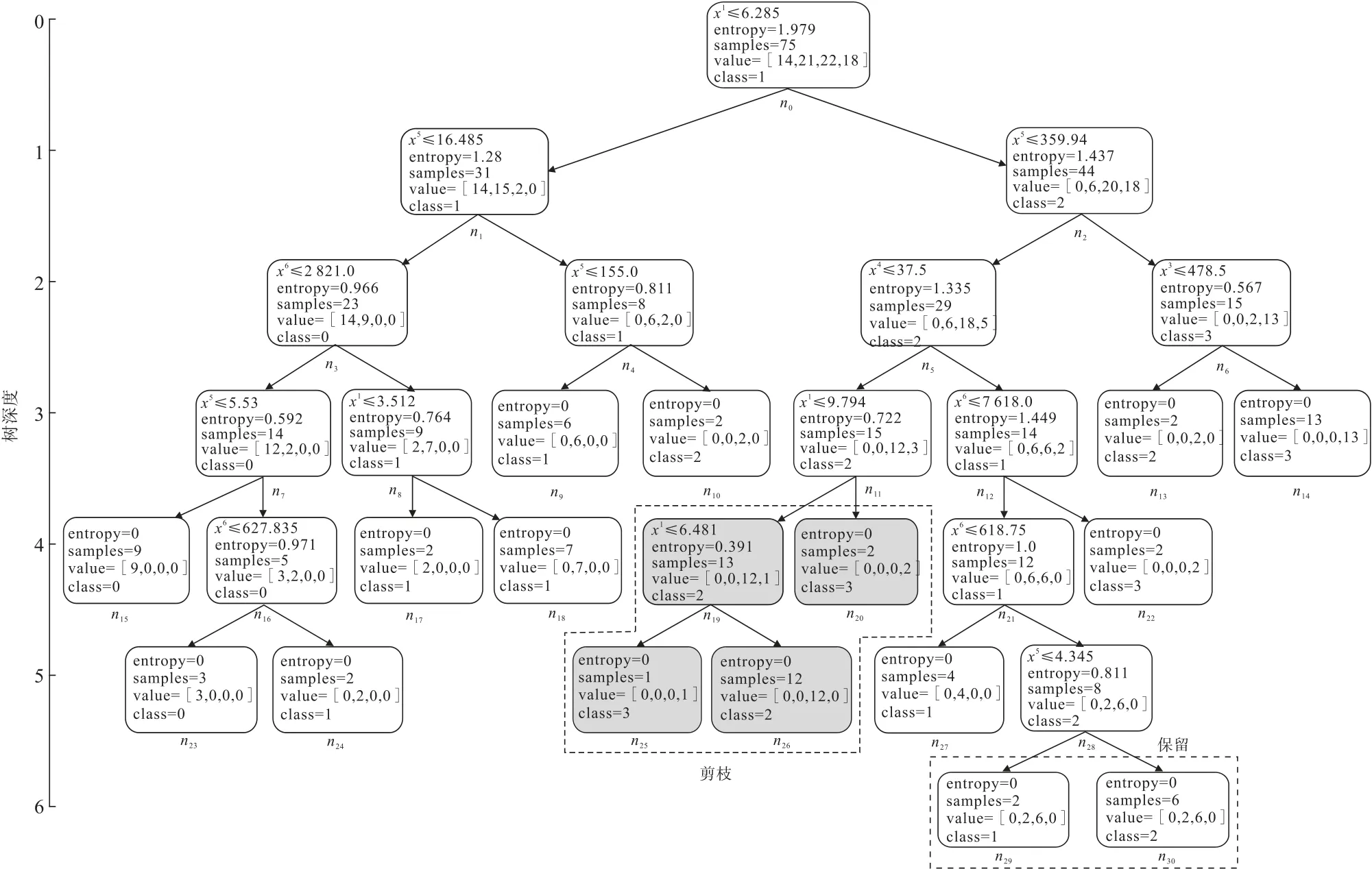
图5 决策树模型的剪枝处理过程Fig.5 The pruning process of decision tree

3.2 模型准确率检验

为了检验透水发生风险评估模型的评估性能,采用测试集样本对初始决策树模型和剪枝决策树模型进行检验评估,检验结果如表4 所示。

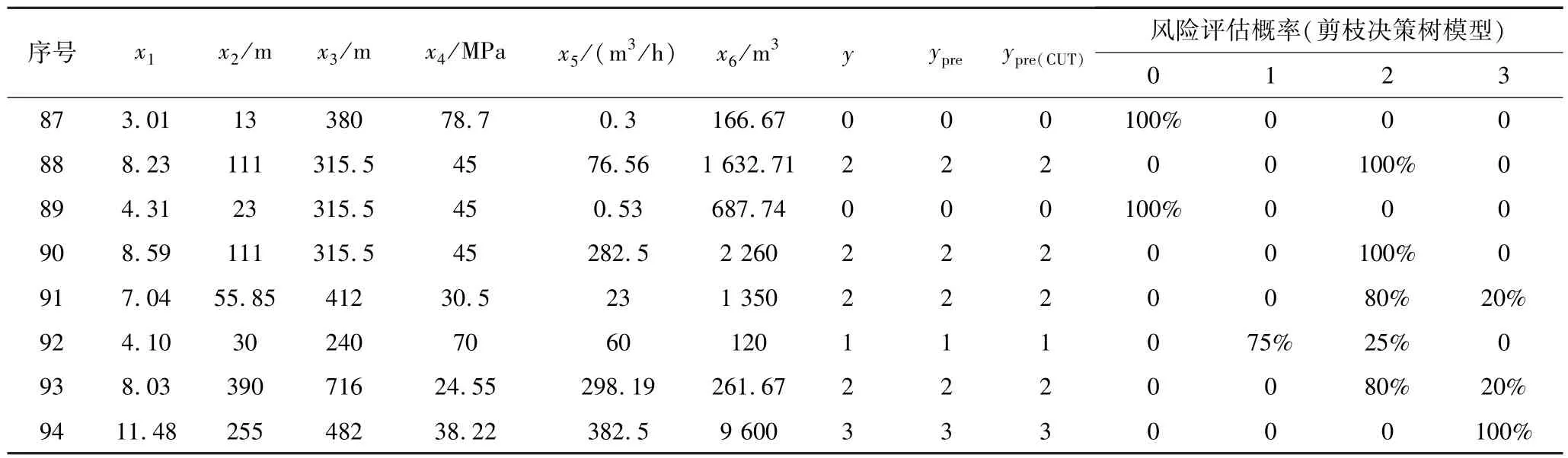
表4 测试集样本数据透水事故发生风险等级检验结果Table 4 Assessment results of water inrush risk level of test set sample data

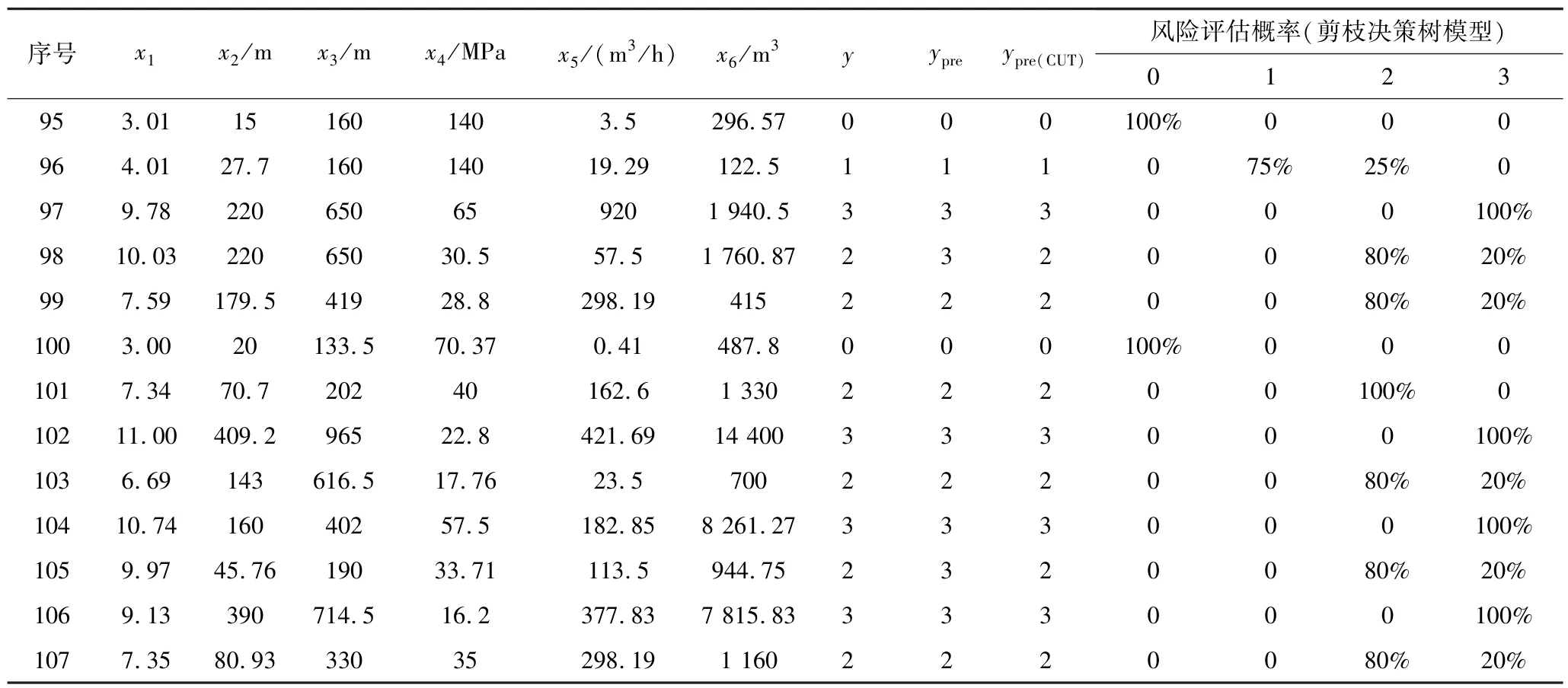
续表4

从表4 可以看出,初始决策树模型评估准确率为90.5%,剪枝决策树模型避免了原模型产生的2 个样本评估偏差,表明剪枝可以有效防止模型过拟合,进而提升评估准确率(从90.5%提升至100%)。在此基础上,进一步采用剪枝决策树模型对107 组透水样本进行了评估(表5),准确率达95.3%,表明剪枝决策树模型具有较强的适用性。

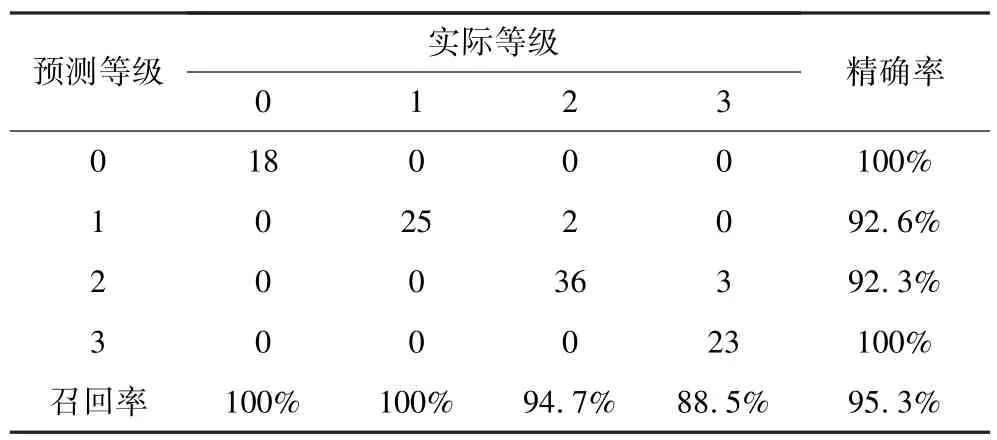
表5 透水事故发生风险评估决策树模型混淆矩阵Table 5 Confusion matrix of decision tree for risk assessment of water inrush hazard

4 结论

本研究以国内外透水事故案例为基础,基于k均值聚类算法确定了事故灾害等级,采用决策树方法建立了透水事故发生风险评估模型,结论如下:

(1)以瞬时最大涌水量和累计涌水量指标,基于k均值聚类算法所划分的107 个透水事故样本灾害等级与其实际灾害等级匹配度较好。

(2)透水事故发生风险评估指标与事故等级具有较好的相关性,其中水文条件加权值、地下水位高程差、埋深、涌水量平均增长速率和累积涌水量与灾害等级呈正相关,岩石饱和单轴抗压强度与灾害等级呈负相关。

(3)剪枝能够有效提高透水事故发生风险评估决策树模型的泛化性能。相对于初始决策树模型,剪枝决策模型对于验证集和测试集样本的评估准确率分别从63.6%和90.5%提高到90.9%和100%,全部样本的综合评估准确率为95.3%,表明该模型具有较好的适用性,能为地下工程透水灾害的救灾决策提供较好的理论和技术支撑。