GNSS高采样率路径增量地图匹配方法

王浩岩，刘远刚，李少华，梁 博，何宗宜,2

1.长江大学地球科学学院，湖北 武汉 430100；2.武汉大学资源与环境科学学院, 湖北 武汉 430079

空间轨迹数据代表了各种运动物体的移动性[1]，且在实时路径规划、路网更新、出行规律发现等诸多领域起着至关重要的作用。由于不同移动设备均存在定位误差，且道路经过地图综合过程已经由真实世界中的面状要素转化为抽象平面下的线状要素，轨迹与其实际所处道路之间存在偏差。因此，在处理和分析轨迹数据之前，应进行地图匹配，使得轨迹被正确的定位在道路之上。在城市应用场景中，全球定位系统技术的进步和大数据处理技术的发展使得城市地区的定位数据以很短的时间间隔获取，如1 s或5 s[2]。如何在兼顾效率及正确率的情况下，满足高采样率轨迹与复杂城市道路网络的匹配成为一项挑战。

地图匹配可在处理实时GNSS数据的在线模式下进行，也可在拥有综合GNSS轨迹信息的离线模式下进行[3]。根据执行匹配操作时所考虑轨迹范围的不同，现有的地图匹配算法又可以分为3类：局部算法、增量算法及全局算法[3]。局部地图匹配算法一次只考虑轨迹上的单个GNSS点，不考虑当前轨迹点与前后点之间的关系。这类方法往往直接基于轨迹点与路段之间的几何关系(如欧氏距离)来判断点所在的路段[4-5]，具有高效和易于实现的优点，但由于忽略了轨迹点之间的时间和空间关系，使得此类算法对空间道路网络数据的创建方式非常敏感[6]，实际应用中极易出现匹配错误的情况。增量地图匹配算法通过考虑相邻点，将拓扑[7-8]、运动状态[9]及转移概率[10-11]等信息引入地图匹配过程，从而提高算法的性能。文献[12]综合考虑影响地图匹配的几何约束与拓扑约束，提出了一种路网拓扑约束下的增量型地图匹配算法，以应对GNSS低频性质带来的匹配不稳定性和复杂城市路网带来的计算复杂性。文献[13]以道路拓扑结构为基础，提出了一种基于道路追踪的矢量道路匹配算法，根据不同道路拓扑结构的变化，进入不同的匹配状态，进行实时匹配修正。文献[14]针对拓扑匹配方法对于起始匹配位置的依赖性，综合利用速度、距离和航向约束改进起始匹配路段和起始位置的判定，以起始位置为基础、速度与时间信息为约束，确定匹配点。文献[15]基于“分治”思想，通过将轨迹点分为相交轨迹点和非相交轨迹点将道路交点与道路区别处理，取得了较好的匹配效果。另外，一些基于动态权重的方法也成为最近的研究热点，这类方法综合考虑多种信息来评估候选集中每条道路的匹配可能[12]。文献[16]提出了一种基于动态权重的地图匹配算法，它的动态权重根据位置精度、速度以及与先前轨迹点的行驶距离计算。文献[17]利用速度、方位差、垂直距离和空间相关性作为轨迹点匹配的影响因素，根据D-S理论(Dempster-Shafer evidence theory)动态估计每个因素的权重。但在增量匹配算法中，先前点的不正确匹配结果可能会累积并影响后续点的匹配[14]。全局地图匹配算法基于相似性度量将整个轨迹映射到道路网络中的路径，由于轨迹上的GNSS点是分批考虑的，所以不会产生增量方法的误差传播问题。因此这类算法对采样率不太敏感，保证在不同采样率下均有较高匹配精度，但同时也导致了高采样率情形下的低效率问题。早期的全局匹配算法基于几何的思路进行相似性度量，其中Hausdorff距离与Fréchet距离为两个较为经典的相似性度量指标，但由于它们的计算公式中都包含最大化算子，使得基于这两种方法的相似性度量均存在对异常值敏感的问题[18]。为了解决这一问题，更多的因子被引入到匹配过程，文献[19]提出了一种时空匹配方法(ST matching method)，该方法将道路网络的空间几何和拓扑结构以及轨迹的时间、速度约束作为匹配特征来搜索匹配的子路径，然后利用候选图来确定全局最优匹配路径。文献[20]使用由几何似然、拓扑似然和时间似然组成的3部分似然函数，从候选集中获得最佳匹配。文献[21]提出保留在轨迹中的弯曲度可用于搜索最相似的匹配路径，并在复杂路段的匹配中取得较好效果。另外，一些先进的算法也被应用于全局匹配，如隐马尔科夫模型(HMM)[22-27]、粒子滤波器[28]、模糊逻辑模型[29-30]和条件随机场[31]等，其中隐马尔科夫模型由于其对噪声不敏感，匹配精度较稳定等特性被广泛应用于各类地图匹配场景中，在满足齐次马尔科夫假设和独立观测假设的条件下，该算法将每个采样点的候选路段作为整条轨迹中的一个隐状态,通过计算发射概率与相邻状态之间的转移概率,获取全局可能性最高的路径。

根据上述各类算法的特点，在面向高采样率与复杂城市路网应用场景时，基于增量的匹配思路被更为广泛的应用，但已有的相关算法在处理高采样率轨迹时，仍存在以下两个问题：①算法匹配时间不仅与轨迹点数量有关，也与车辆行驶路段的复杂程度密切相关，更高的采样率及道路复杂度带来了更为耗时的计算过程；②在路口点等复杂路段处，由于移动物体通常以低速进行移动，使得轨迹点间距离相对于其他区域更小，从而也容易导致错误匹配。针对以上两个问题，本文主要关注在离线场景中算法性能的优化，提出一种基于路径增量的地图匹配方法，能够在提高计算效率的同时较好地处理复杂路段处的轨迹匹配问题，为解决相关问题提供有益思路。

1 基本概念与总体思路

1.1 道路匹配基本概念

轨迹T为移动设备所采集的位置点的集合，可以表示为T={pi|i=1,2,…,N}。路网为真实道路系统的数字表达，可以通过有向图G(V,E)来描述，其中V为顶点的集合{vj|j=1,2,…,M}，E为边的集合{ek|k=1,2,…,O}，顶点vj相关联边的数目称为顶点vj的度，记作d(vj)。对于任意顶点vj，若d(vj)=1，称vj为单连通点；若d(vj)=2，称vj为过渡点；若d(vj)≥3，称vj为路口点。将G(V,E)中的边称为路段，路径P为一系列相连的路段的集合，表示为P={e0,e1,…,ej}。候选轨迹点为落在顶点vj邻近区域内的轨迹点集，记作I(vj)，下文将候选轨迹点简称为候选点。候选路段集为与轨迹点pi的误差分布范围相交路段的集合，表示为C(pi)。道路子网G′(V′,E′)为经过过滤处理后，用于进行地图匹配的路网，即G′⊆G，满足V′⊆V,E′⊆E。

本文定义增量为两个相邻路口点之间的路径，则可将地图匹配抽象为根据轨迹T及路网G(V,E)，构建道路子网G′(V′,E′)，进行增量计算并最终确定物体实际运动路径的过程。

1.2 匹配算法总体设计

本文算法旨在解决高采样率轨迹在复杂路网中的地图匹配问题，提高匹配效率以及优化复杂路段处的匹配是本文算法的重点。算法可大致分为两个部分：复杂道路网络的组合过滤和针对道路子网的增量匹配过程，具体流程如图1所示。在组合过滤部分，通过对路网G(V,E)的逐步过滤获得道路子网G′(V′,E′)，首先采用距离约束过滤获取候选路段集，然后基于道路连通性与方向一致性约束过滤无连通路段以及方向偏差较大路段，最后基于首尾路段识别结果，剪除单点连通路段，从而对复杂路网进行简化，以减少后续增量过程中错误匹配的可能性以及不必要的耗时。在增量匹配部分，首先确定物体运动的起始路段，然后进行逐步增量计算以确定轨迹的匹配路径；每一个增量计算过程均以路口点为起点(初次计算起点为起始路段的单连通点)，确定后续匹配路段，当匹配路段连接顶点为过渡点时则记录当前路段，继续确定下一路段，当匹配路段连接的顶点为路口点时，则进入下一个增量计算过程，直到出现单连通点(此时为终止路段)，匹配过程结束；在路口点处进行增量前进方向判断的过程中，采用综合Hausdorff距离及弯曲度特征的相似度评价方案进行路口点处候选点及连接路段的匹配，以减弱平行同向路段对匹配结果的影响，提高轨迹匹配精度。

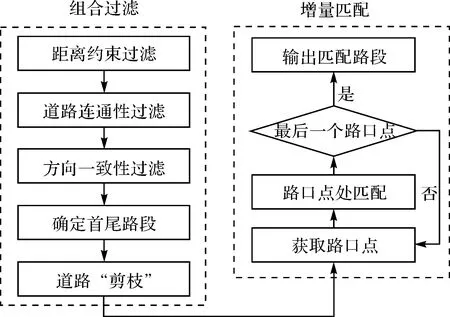
图1 算法流程

2 复杂道路网络的组合过滤

在复杂的城市道路网络中进行地图匹配，难点在于对交叉路口以及平行道路的匹配。该区域的轨迹往往存在多个距离相近且形态相似的候选路段，容易导致错误匹配。因此，仅根据单个轨迹点是难以准确匹配的，需要将相近的轨迹点结合起来，形成运动对象的空间上下文信息。在采样率较高的情况下，通过相近的轨迹点可计算出对象在当前时段内的方向、速度等运动状态，再结合附近路网的相关特征，一些无关路段可被剔除。理论上考虑的轨迹点越多匹配准确性越高，但计算成本也越高。因此，本文将相邻两个轨迹点的上下文信息与其附近道路的连通性、方向等特征结合，对候选路段进行过滤，剔除大量无关路段。图2为道路网过滤结果的示意，其中原路网经过距离、连通性、方向等一系列条件过滤和“剪枝”后得到与轨迹点比较匹配的候选“道路子网”。

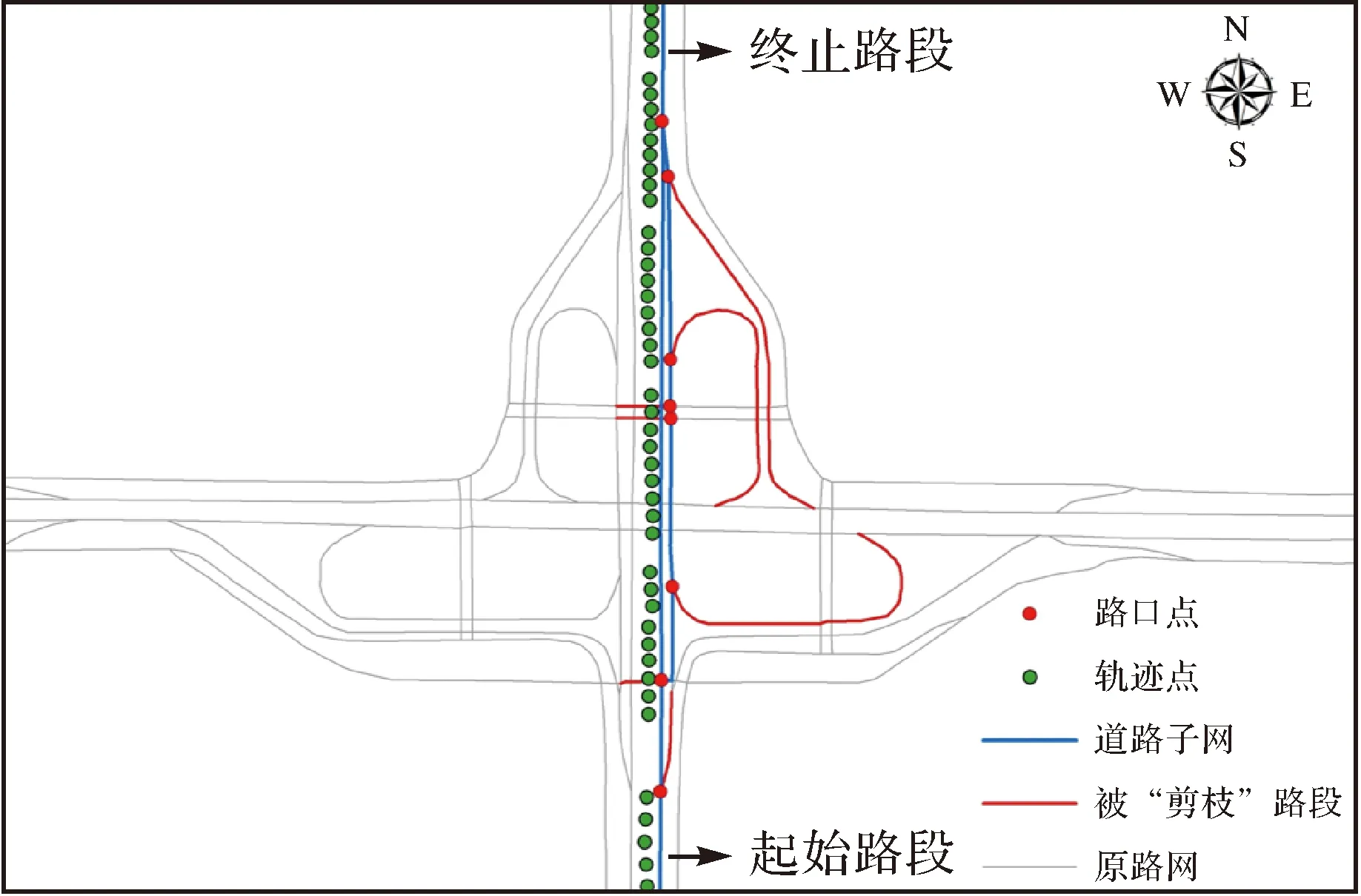
图2 过滤结果示例

2.1 距离约束过滤

地图匹配的关键假设是GNSS定位存在误差，且误差是在一定的范围内[12]。将误差范围作为距离约束可以对路网进行初步过滤，构建初始候选路段集，合适的误差范围对于提高算法的精度及效率有着重要的意义。本文采用误差圆构建缓冲区，刻画轨迹点误差范围。已有研究表明，轨迹点的误差与速度存在相关性，当运动物体速度变大时，定位误差会在一定程度上减小[6]。可见，各轨迹点的误差半径并非固定，需要设置一个合理范围。若半径设置过小，会导致正确的路段被排除在外，反之，当半径设置过大时，会增加匹配的计算量。因此，本文候选路段集通过一种动态调整的缓冲区选取，即以轨迹点为圆心初始半径rp0构建缓冲区，若候选路段集为空，则将半径扩大一个固定的步长rpstep，如此循环，直到候选路段集中至少包含一条路段为止。

2.2 道路连通性过滤

在以往的研究中，对于高采样率轨迹一般指采样间隔在30 s以内的轨迹[32]，但运动对象的速度并不一致，当运动对象的速度较大时，轨迹间的距离也会变大，在低采样率轨迹匹配中出现的“跳弧”现象也同样会在高采样率轨迹中出现。为避免因这一问题所带来的歧义，本文将高采样率轨迹定义为候选路段能够满足拓扑连通性的轨迹，基于这一定义即可对候选路段进行道路连通性的过滤。

根据城市道路通行规则将路段分为两类：单向(通行)路段与双向(通行)路段。在城市路网中，单向路段往往在复杂的交叉路口以及平行道路中大量出现，这类路段在地图匹配过程中更容易出现匹配错误。道路连通性反映的是前后路段之间的连通关系，根据前后连接路段类型的不同，可以进一步将其连接关系分为单向路段与单向路段的连接，单向路段与双向路段的连接以及双向路段与双向路段的连接。针对上述连接关系的特征，本文主要考虑了两方面的连通性约束。

(1)拓扑连通性约束：基于缓冲区选择的候选路段中，存在大量在几何上相交但实际不具备连通性的路段，拓扑连通性约束是剔除这类路段的主要工具。其定义为对于轨迹中的任一点pi，其候选路段集C(pi)中存在路段ei与候选路段集C(pi+1)中某一路段ej端点相连或重叠。不满足这一约束的路段将被剔除。

(2)方向连通性约束：如图3(a)所示，对于单向通行路径，其中的路段可抽象为一组有向线段，如果这组线段方向一致，则满足方向连通性约束。其定义为对于轨迹中任一点pi，候选路段集C(pi)中存在路段ei与候选路段集C(pi+1)中某一路段ej相连或重叠，且当ei与ej相连时，应同时满足两路段方向在连接处首尾相接。图3(b)中反映了两类满足拓扑连通性而不具备方向连通性的情况，这样的路段应该被过滤。由于双向路段没有方向限制，故仅需要考虑单向路段相互连接时的方向连通性约束。

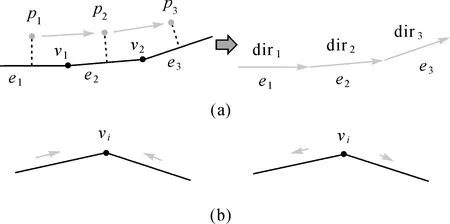
图3 方向连通性

2.3 方向一致性过滤

在运动过程中轨迹方向与其实际行驶道路的方向应该是一致的，基于这一特性可以将候选路段中方向与轨迹方向有较大差别的路段剔除。方向一致性过滤应用于单向路段与双向路段的连接以及单向路段与单向路段的连接，在单向路段与双向路段的连接情况下，以单向路段方向作为连接路段方向。方向一致性过滤需要经过长度比过滤与方位角过滤两个步骤。

(1)长度比过滤：如图4(a)所示，p1、p2为两个连续的轨迹点，P1、P2与P3为3条包含候选路段的路径，且这3条路径均可作为p1，p2的匹配路径，p1、p2在其对应候选路段上的投影即为该轨迹点的实际位置，对于高采样率的轨迹，它们的分布与实际所在的路段通常呈近似平行的关系。基于这一认识，在进行轨迹方向与路段方向对比前，通过连续轨迹点之间的距离与其在候选路段上投影点之间距离的长度比剔除横向路段，同时避免轨迹顺序与对应候选路段顺序不一致的情况。根据试验这一比值设为0.8时，能达到较好的剔除效果。在图4(a)中，轨迹点向P3投影后的长度Len3远小于轨迹点之间的距离，从而可以将路径P3剔除。

(2)方位角过滤：如图4(b)所示，在完成长度比过滤后，剩下的即为两条方向相反的路径，通过计算轨迹与轨迹在路径上投影点之间的向量方位角之差可以剔除方向相反的路径，其中向量的方位角为正北方向沿顺时针旋转至当前向量所经过的水平角度，计算公式为

(1)

式中，α为当前向量的方位角；(x1,y1)、(x2,y2)分别为向量的首尾点坐标。

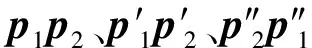
图4 方向一致性过滤

2.4 单点连通路段“剪枝”

在完成上述过滤步骤后，满足连通性和方向一致性的路段被保留了下来。在这些剩余的路段构成的子网中，除了首尾路段之外，若还存在其他路段的顶点度数为1，则可将它们“剪枝”，因为这类单点连通路段不可能作为最终匹配路径上的中间路段。图2中经过连通性、方向一致性约束过滤后的路网中仍存在单点连通路段，即被“剪枝”路段(红色)，它们会增加后续地图匹配的运算量，需要剔除。算法中，基于这一规则依次遍历各个路段，分别计算各路段起点与终点的度数，删除除首尾路段之外的其他单点连通路段即可。其中确定首尾路段的方法作为本文增量匹配算法的关键问题在3.2.2节中详细介绍。

3 基于路径的增量匹配算法

3.1 相似度评价

在基于几何特征的匹配方法中，一般采用距离、角度等几何特征进行轨迹点的匹配。采用Hausdorff距离作为距离因子，可以有效降低相似平行路段带来的误差。当匹配的路网较为复杂时，仅仅依赖距离和角度因子容易出现错误匹配，而弯曲度作为一种内在的几何特征，在采集的GNSS轨迹中被很好地保留，且轨迹与其行驶路段的弯曲度特征高度一致，从而可以用于进一步提升匹配精度。本文采用基于Hausdorff距离和弯曲度的相似度评价方法。

3.1.1 距离因子

在路口点的匹配中，需要将连续的轨迹点匹配到路口点相关的前后两个路段上，距离评价因子为上述两组点之间的距离的映射。Hausdorff距离是描述两组点之间相似程度的一种量度，本文采用Hausdorff距离计算轨迹点与轨迹在匹配路段上的投影点之间的距离。其定义[18]为：假设有两组集合A={a1,a2,…,ap},B={b1,b2,…,bq}，这两组点之间的Hausdorff距离为

H(A,B)=max(h(A,B),h(B,A))

(2)

式中，h(A,B)=max min‖a-b‖，(a∈A,b∈B)；h(B,A)=max min‖b-a‖，(a∈A,b∈B)；‖*‖为点集A与点集B之间的距离范数。

3.1.2 弯曲度因子

弯曲度因子用于描述路口点处候选点与待匹配路段的几何形态特征。在光滑曲线中采用曲率描述某点处的弯曲程度，其定义为γ(s)是二维平面上一条以弧长为参数的光滑曲线，在曲线上存在点M与点N，其中点M对应弧长为s，在点M处切向量的倾角为α，点N对应弧长为s+Δs，在点N处的切向量的倾角为α+Δα，则曲线γ(s)在点M处的曲率为

(3)

式中，Δα为M、N两点间切线的转角，其值域为(-π,π]；Δs为M、N两点间弧长的变化。

在一段弧长上总的曲率变化可以通过曲率的积分表示，在上述以弧长为参数的光滑曲线γ(s)上，M、N之间的曲率积分可以表示为

(4)

式中，K(M,N)为点M、N之间的曲率积分；k为弧段上某点处的曲率，即M、N两点之间的曲率积分描述了从点M出发沿γ(s)移动到点N所转过的角度。

但在地图匹配问题中，轨迹及道路均被离散化为点的序列，本文参考文献[21]中对于离散点序列曲率积分的计算方法，采用离散化后点序列中前后相邻的两个点形成的向量来近似表示该位置的切向量。假设平滑曲线γ被离散化为点序列[a1,a2,…,an]，则离散化后曲线的曲率积分为

(5)

式中，在计算各点曲率时，以正北方向作为基准，采用方位角代替原公式中的倾角，式(1)为方位角的计算方式。

3.1.3 相似度计算

路口点处的相似度为上述两个因子的综合，表达式为

(6)

式中，Hdif为轨迹与对应路径之间的Hausdorff距离的差值的绝对值；Kdif为轨迹与对应道路的曲率积分差的绝对值，相似度的值域为(0,1]，值越大时则当前路径与轨迹越为相似。

3.2 增量匹配

3.2.1 增量匹配过程

在现实世界中，物体沿道路的运动通常为沿路线移动并在路口处判断前进方向的过程，当确定了某一段路径的首尾点后，它们之间的路径往往是唯一的，所以物体移动的过程可以被抽象为沿运动方向的增量计算。在传统的增量匹配方法中，通常是将轨迹点或者轨迹片段作为增量，但未能充分重视因道路的复杂性导致的错误匹配，同时在处理高采样率轨迹时也带来了更高的时间成本。基于路口点的增量匹配方法在前文过滤器的基础上将两个相邻路口点之间的路径作为增量，将轨迹与路段的匹配问题转化为路口点处的方向选择问题。

算法通过道路子网的顶点类型来控制匹配的过程，在确定初始路段后，进入增量计算过程，当路段终点为单连通点时，此时为终止路段，匹配过程结束；当路段终点为过渡点时，此时路段的选择是唯一的；当路段终点为路口点时，此时为下一增量的起点，进行路口点匹配。算法1为增量匹配过程的伪代码。

算法1：增量匹配过程

输入：轨迹Trcak，道路子网G′

输出：匹配路径P

调用算法2，确定起始路段startSection

P.append(startSection)

获取起始路段终点estart.lastPoint

vjudge←estart.lastPoint #初始化当前判断点

ejudge←estart#初始化当前判断路段

while True:

获取与当前判断点连接的路段列表E

if len(E)=1: #当E中路段数量为1时

break

else if len(E)=2: #当E中路段数量为2时

从vjudge的连接路段列表中剔除ejudge，剩下的即为后向路段ebackward

P.append(ebackward)

ejudge←ebackward

vjudge←ebackward.lastPoint

else if len(E)>=3: #当E中路段数量大于或等于3时

调用算法3，完成路口点的匹配操作，获取ebackward

P.append(ebackward)

ejudge←ebackward

vjudge←ebackward.lastPoint

3.2.2 首尾路段的确定

增量算法中起始位置匹配误差会随着道路的延续而传递累计[14]。所以，首尾点路段的识别对本文匹配算法的成败至关重要，同时也决定了哪些单连通路段可以被提前“剪枝”。本文参考“前瞻”[33]思想进行首尾路段的确定，算法2为起始路段的确定方法，对于终止路段的确定，以终止轨迹点作为起点进行逆向判断即可。需要注意的是当候选路段所对应的路口点相同时，根据该路口点处路段匹配结果即可确定起止路段；当候选路段所对应的路口点不同时，则分别针对不同路口点处进行路段匹配，然后选取与轨迹相似度更高的路段作为起止路段。如图5所示，e1、e2为起始轨迹点p1的候选路段，图5(a)中e1、e2对应于同一路口点v1，在v1处执行匹配，可以确定e1为起始路段；图5(b)中e1、e2分别对应于路口点v1、v2，此时分别进行匹配并比较相似度即可确定起始路段。

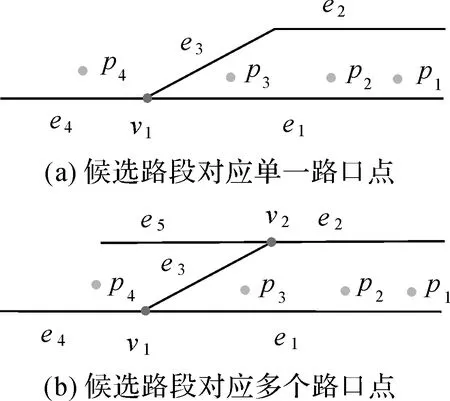
图5 首尾路段的选择

算法2：起始路段的确定

输入：轨迹Trcak，“剪枝”前路网filterRoads

输出：起始路段startSection

i←0

startSection←filterRoads[0] #初始化起始路段

while True:

获取候选路段集C(Trcak[i])

if len(C(Trcak[i]))=0: #当候选路段集中路段数量为0时

i←i+1

else if len(C(Trcak[i]))=1: #当候选路段集中路段数量为1时

startSection←C(Trcak[i])[0]

break

else if len(C(Trcak[i]))≥2: #当候选路段集中路段数量大于或等于2时

根据式(7)计算与候选路段连接的路口点处的相似度

确定最优起始路段esimmax

startSection←esimmax

break

3.2.3 路口点处的匹配

路口点处的匹配用于确定增量匹配的方向，算法3描述了匹配过程。首先基于路口点与搜索半径构建候选点集I，然后获取候选点与其在对应路段上的投影点，计算轨迹与路段的相似度，最终通过对比相似度确定增量匹配方向。图6描述了路口点v1的匹配过程，如图6(a)所示，e1为上一增量已经匹配的路段，v1为下一个增量匹配的起点，此时需要确定后续增量的匹配方向，即从路径e1→e2和e1→e3中确定与轨迹匹配的路径，图6(b)、(c)分别刻画了两种不同路径的匹配过程，通过计算轨迹与其投影点两组点集之间的相似度可以较容易地确定e3为后续的匹配路段。其中，候选点集I应同时包含已通过及未通过路口点的轨迹点，否则以步长rcstep逐步增加搜索半径rc的长度，直到条件满足。

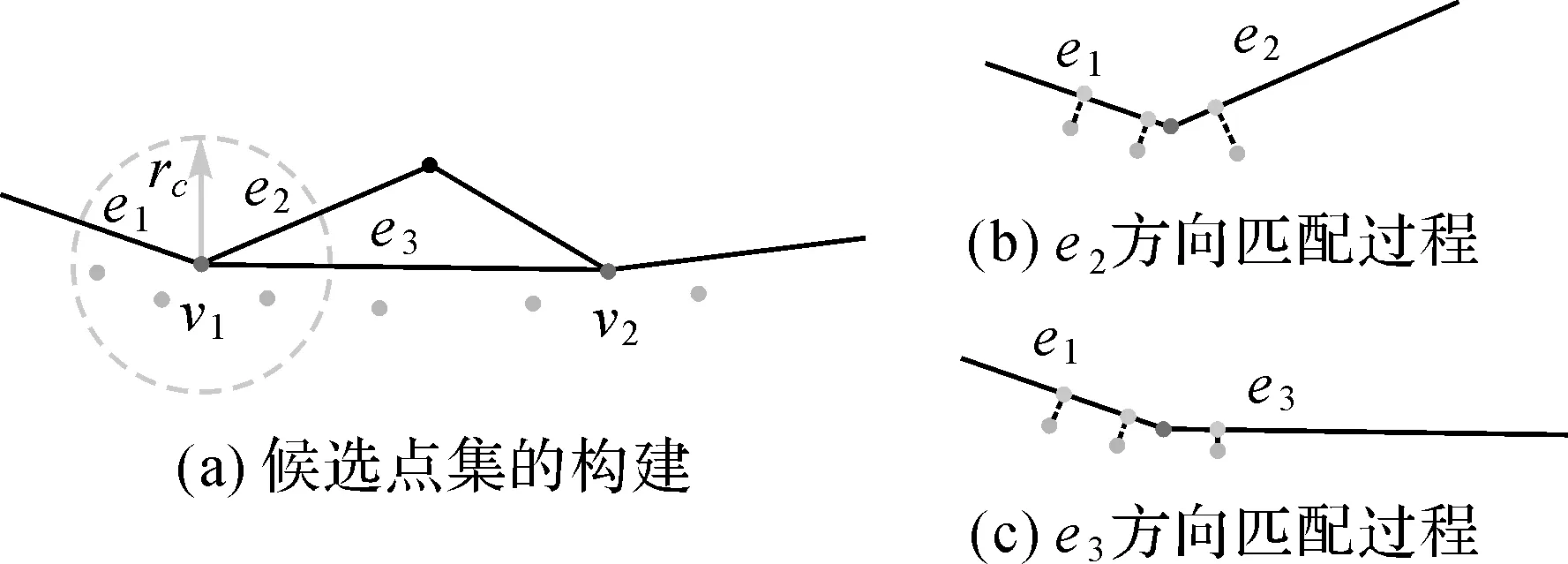
图6 路口点处匹配过程

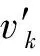
图7 候选点位置判断

算法3：路口点处匹配

输入：轨迹Trcak，当前判断点vjudge，当前判断路段ejudge，与vjudge连接的路段列表E

输出：匹配路段ematch

获取vjudge的候选点集I#此时vjudge为路口点

根据是否通过vjudge将I中的轨迹点分为Ipassed及Ifailed两部分

foreinE:

ife.equals(ejudge):

pass

else:

Iproject←[] #初始化投影点集

计算Ifailed中轨迹点在ejudge上的投影点，并添加至Iproject

Iproject.append(vjudge)

计算Ipassed中轨迹点在e上的投影点，并添加至Iproject

计算I与Iproject之间的相似度

获取相似度最高的路段esimmax

ematch←esimmax

4 试验与讨论

4.1 试验数据预处理

为验证算法的有效性，本文从微软亚洲研究院提供的GeoLife 1.3公开数据集中选取了部分出租车轨迹进行试验，轨迹采样间隔为1 s。路网数据为北京市的道路交通网络，选取轨迹所经过路段中包含大量平行路段、复杂交叉路口等特殊路段，测试轨迹如图8所示，相关信息见表1。

图8 测试轨迹

表1 测试轨迹信息表

在进行匹配工作前，需要对轨迹数据进行预处理，基于移动速度剔除轨迹中可能存在的异常轨迹点，异常轨迹点可分为两类：①轨迹移动速度远低于正常行驶速度或停滞的点；②由于定位误差造成的偏离正常轨迹范围的点。这两类异常点均表现为速度上的异常，可通过速度阈值剔除，试验中剔除了速度小于1 m/s或速度大于35 m/s的异常点。

试验主机环境为AMD Ryzen 5 3600 6-Core Processor CPU @3.60 GHz、16.0 GB RAM、WIN10 x64；采用的编程环境为Python 3.6。

4.2 试验结果及对比分析

为更好地验证算法的效果，将本文算法与曲率积分约束的地图匹配算法(以下简称为“曲率积分算法”)[21]及HMM算法[22]进行对比。主要从匹配结果的精度及效率角度对算法进行测试。为评价算法匹配精度，本文借鉴文献[34]中评价方法，将评价指标设为：路径不匹配分数(route mismatch fraction，RMF)，准确率(Precision)，召回率(Recall)，具体定义如式(7)—式(9)所示

(7)

(8)

(9)

式中，L+为算法计算结果中与真实路径相比错误增加的长度；L-为算法计算结果中与真实路径相比错误减少的长度；Lmatched为算法计算结果中正确匹配路径的总长度；Linferred为算法计算结果的总长度；Lreal为真实路径的总长度。

考虑试验数据集中的GNSS定位误差和道路宽度，将候选路段缓冲区半径rp和候选点缓冲区半径rc的初始长度均设为30 m，对应的步长设为5 m。同时,为比较相关算法在不同采样频率下的匹配性能,本文逐步提高采样间隔至10 s，按照文献内的描述实现了相应算法，并利用上述指标进行对比试验。

匹配结果指标统计如图9中所示，在测试数据集中当采样间隔为1 s时，本文算法的准确率达97.70%，召回率达97.10%，RMF为5.23%，相对于其他两类算法均有较大提升，表明在高采样率下本文算法能够保证较高的匹配正确率。其原因主要包括两个方面：①算法过滤器滤去了绝大部分错误路段，大大降低了错误匹配的可能性；图10为采样间隔为1 s时各数据集的匹配结果，其中红色线条为本文算法匹配结果，绿色线条为曲率积分算法匹配结果，蓝色算法为HMM算法匹配结果，灰色线条为北京市路网；可以看出HMM算法在匹配中出现了大量将轨迹匹配至方向相反路段的情况，而本文算法匹配前已过滤掉了反方向路段。②基于本文增量算法的匹配过程保证了路口点间路径的唯一性，减弱了平行路段对匹配结果可能带来的不利影响；如图10(b)所示，曲率积分算法出现了两条平行路段均被选择的情况，其原因在于该方法是基于点对选择匹配路段的，当轨迹采样率较高时，同向平行的两个路段可能在不同点对中被选择，从而导致错误匹配，而本文算法则避免了对于平行路段的错误选择。同时，算法在利用多层互通进行行驶方向变化的复杂场景的匹配中也表现出了较好的效果，其结果如图10(d)所示。但随着采样间隔的提高，路口点匹配中候选点的数量将逐渐减少，使得算法准确率及召回率逐渐降低，且在采样间隔为10 s左右时已无明显的优势，说明本文算法对采样率变化较为敏感。但由于算法获取路径的唯一性，RMF仍然明显优于其他算法。

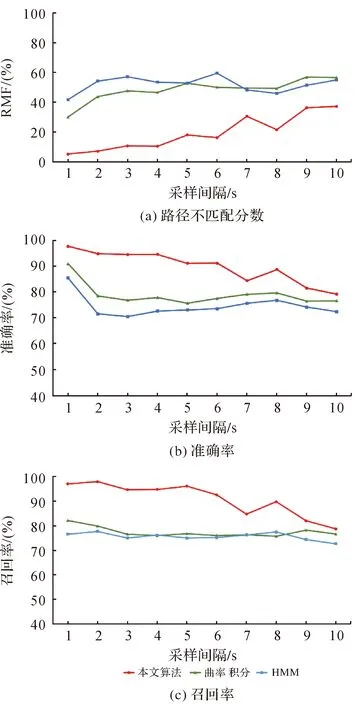
图9 地图匹配精度评价指标

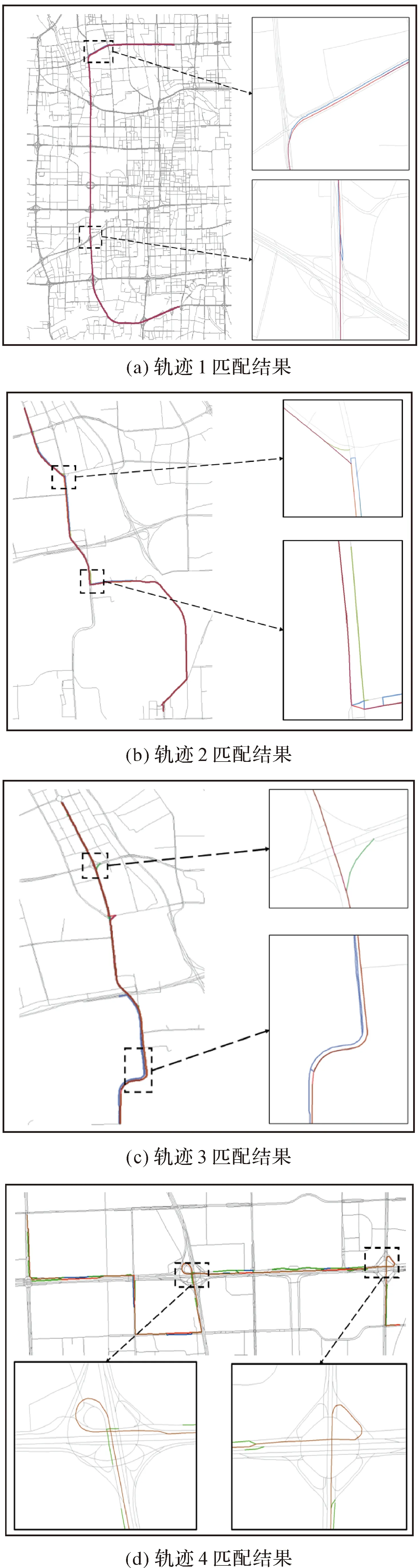
图10 轨迹匹配结果

另外，对各类算法效率进行统计，结果如图11所示。采样间隔越短，本文算法的效率优势越明显。其原因在于两种对比算法中匹配单元的调用次数与轨迹点的数量密切相关，而匹配单元的频繁调用无疑会导致更高的时间成本。而本文算法通过以路径为增量，使得计算单元的调用次数仅与路网中路口点个数相关，而路网经过组合过滤后，复杂度大大降低，从而实现了效率的进一步提高。图12为采样间隔为1 s时各算法中匹配单元的调用次数，当轨迹采样间隔较短时，轨迹点数量远大于需要匹配的路口点的数量，所以本文算法匹配单元的调用次数远远低于其他两类算法，从而使得算法效率得到明显提升。随着采样间隔的增加，轨迹点数量逐渐减少，但路口点的个数不变，故本算法效率优势将会逐渐消失，最终与全局匹配算法的效率接近。

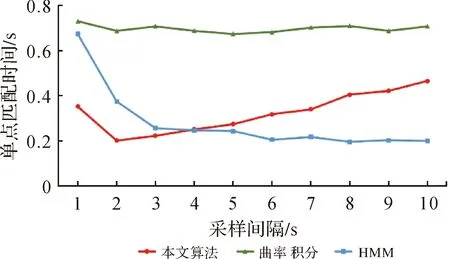
图11 算法效率

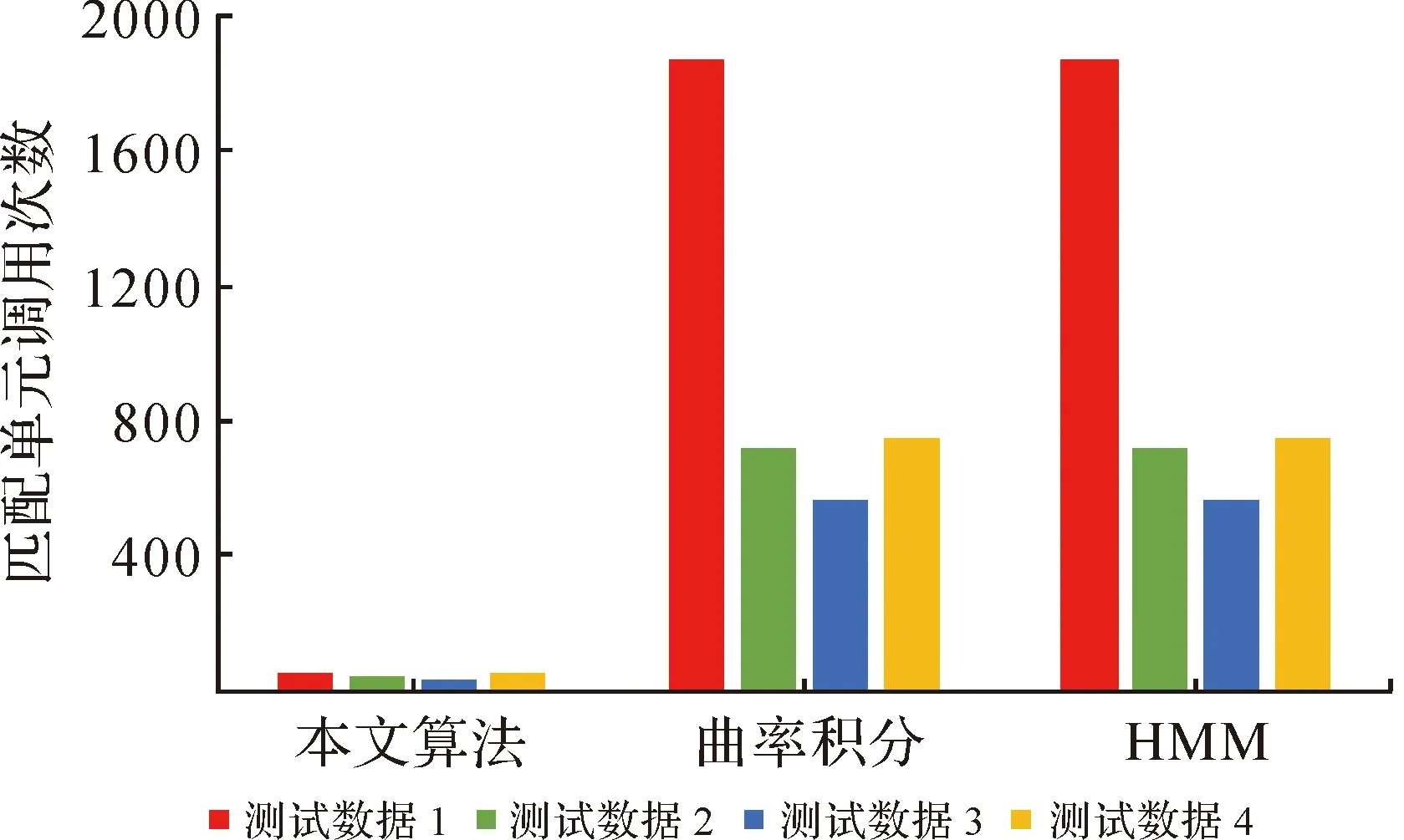
图12 匹配单元调用次数

5 结 论

本文提出了一种高采样率轨迹数据在复杂城市路网中的增量匹配方法，提高匹配效率的同时兼顾了对于复杂路段的处理。算法通过对路网的组合过滤消除了无连通路段及反向路段对匹配过程的影响，并采用路径增量替代传统增量匹配方法中的轨迹增量，使得匹配结果更加符合真实的车辆行驶路线。在路口点处采用曲率积分与Hausdorff距离的组合代替传统匹配算法中的几何度量以提高起始路段以及路口点处的匹配精度。通过试验验证了本文算法的有效性，较好地解决了高采样率数据在复杂路网匹配中准确率与效率之间的矛盾。

本文匹配算法的核心在于以路口点匹配为基础的路径增量过程，算法对于采样率的变化较为敏感，当采样率较低时，路口点处将有可能出现没有轨迹点的情况，从而导致基于路口点的匹配失效。后续研究将进一步探讨以路径为增量的匹配思路处理低采样率轨迹数据的可行性，增强算法对于不同采样率数据的普适性。