地理加权回归建模结果不确定性度量与约束方法
刘 宁,邹 滨,张鸿辉
1.中南大学地球科学与信息物理学院,湖南 长沙 410083; 2.广东国地规划科技股份有限公司,广东 广州 510075; 3.湖南师范大学资源与环境科学学院,湖南 长沙 410012
地理加权回归(geographically weighted regression,GWR)是通过假设回归点仅与空间一定范围观测点有关而建立起的一种局部加权最小二乘模型[1]。建模过程中,首先基于修正赤池信息量准则或留一交叉验证准则搜索空间带宽[2-3],确定影响回归点的临近观测点;然后构建距离衰减权重函数对临近观测点定权后,通过局部加权最小二乘估算回归点系数值与预测值[1]。该模型在探索自然地理及社会人文现象的空间分布、空间非平稳性及空间尺度转换等多个领域有着广泛的应用。文献[4]采用GWR模型估算了全国PM2.5浓度空间分布。文献[5]基于GWR模型揭示了上海房价的空间分异特征及其显著影响因素。文献[6]通过GWR模型将遥感MODIS降水量产品从990 m分辨率提升至90 m精细尺度。
然而受空间样本稀疏与局部共线性等因素影响,GWR建模结果不确定性往往呈现空间异质性[7]。文献[8]在住宅地价估算的修正研究中发现,回归样本点密度降低时,GWR模型估算精度不可避免随之下降。文献[9—11]发现,当局部区域两个或多个自变量存在共线性问题时,GWR模型回归预测结果常出现奇异值,回归系数符号甚至偏离预期。
针对上述问题,文献[12]尝试将主成分分析(principle component analysis,PCA)方法引入GWR建模过程,即预先用PCA方法对GWR自变量进行降维转换,通过仅保留自变量主要信息的方式弱化其相关性达到解决局部共线性问题的目的,但转换后的自变量常失去原有物理含义。同时也有学者通过对自变量单独构建空间带宽[13-14]、引入岭回归思路[15]减弱局部共线性影响,或引入条件数[16]、方差膨胀系数[17]等多个指标甄别共线性问题,但这些方法与指标仍都无法表征由样本稀疏造成的GWR模型估算精度衰减。
对此,本文拟在依据协方差传播定律构建后验标准差评估指标基础上[18-19],提出一种地理加权回归建模结果不确定性度量与约束方法,并基于卫星遥感估算地表PM2.5浓度实例与传统条件数约束方法开展对比,验证该方法的可靠性。
1 后验标准差约束下的GWR模型
1.1 GWR模型原理
空间位置为(μi,vi)的GWR局部回归模型[1]为
(1)
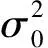
由式(1)可知,系数βj(μi,vi)与β0(μi,vi)为空间位置的函数。位置(μi,vi)的回归系数列向量β(μi,vi)=[β0(μi,vi);β1(μi,vi);…;βm(μi,vi)]由局部最小加权二乘估计
(2)
式中,y=[y1y2…yn]为n个点位下的观测列矢量;X为自变量矩阵为
(3)
式中,W(μi,vi)为点位(μi,vi)的对角权阵,其对角阵元素为[w1,iw2,i…wn,i],wk,i代表了k点位对i点位影响的权重值,权重由随距离衰减的核函数构造,常用核函数有Guassian与Bisquare等[1,20]
(4)
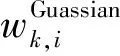
回归系数β(μi,vi)由式(2)估计得出后,点位(μi,vi)的GWR估计值为
(5)
式中,xi为自变量矩阵第i行向量。
1.2 后验标准差约束下GWR优化
设Ri=(XTW(μi,vi)X)-1XTW(μi,vi)、Si=xiRi,则式(2)与式(5)可重写为
(6)
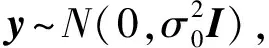
(7)

(8)

(9)
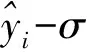

图1 GWR估算值在均值为标准差分别为σ1、σ2、σ3时的正态分布曲线
本文拟通过剔除后验标准差较大的GWR估算值提升GWR模型的总体精度。具体而言,①基于式(5)与式(7)计算每个样本点的十折交叉验证值[22]及其后验SD值;②设置SD阈值,剔除后验SD值大于阈值的样本点;③比较剩余样本的十折交叉验证值与观测值,评估十折交叉验证精度;④精度不满足要求则降低SD阈值重复②—④步,满足要求则以当前SD阈值约束GWR估算值。算法流程图如图2所示。

图2 后验标准差约束下的GWR模型建模流程
2 试验设计与结果分析
2.1 数据源与预处理
本文以2019年基于地理加权回归模型的中国区域近地表PM2.5浓度遥感制图试验进行验证。模型因变量为来自中国环境监测总站发布的1356个地面站点PM2.5小时浓度数据(http:∥www.cnemc.cn/)。模型自变量包括遥感气溶胶光学厚度(aerosol optical depth,AOD)、气象数据及增强型植被指数(enhanced vegetation index,EVI)。遥感AOD与EVI数据均为NASA Terra/Aqua MODIS传感器(https:∥ladsweb.modaps.eosdis.nasa.gov/)所反演的一天两次的1 km产品,其两次的过境时刻分别为当地时间10:30 a.m.与13:30 p.m.左右。ERA5气象数据来自第五代ECMWF大气再分析全球气候产品(https:∥cds.climate.copernicus.eu/),选取的气象变量分别为边界层高度、相对湿度、地表气压、2 m气温、经向风速、纬向风速。ERA5气象数据的空间分辨率为0.1°~0.25°,时间分辨率为1 h。
采用最邻近插值以及样条函数插值方法将EVI和气象等要素值降尺度至遥感AOD网格,再将EVI、气象、AOD等网格化自变量值与地面站点PM2.5浓度值进行时空匹配。剔除因云雨天气及积雪覆盖等导致的无效值后,共计生成236 206个样本数据。此外,为使GWR模型估算的回归系数不受不同变量之间量级差异的影响,在GWR建模前对所有自变量与因变量均基于z-score方法开展了标准化处理。表1为因变量地面站点PM2.5浓度数据与自变量AOD/EVI等数据的统计信息。在此基础上,本文在365 d Terra/Aqua过境时刻共建立了730个模型。通过建立的GWR模型,估算近地表PM2.5遥感制图结果及其不确定性,最后再将近地表PM2.5遥感制图结果反标准化为浓度值。
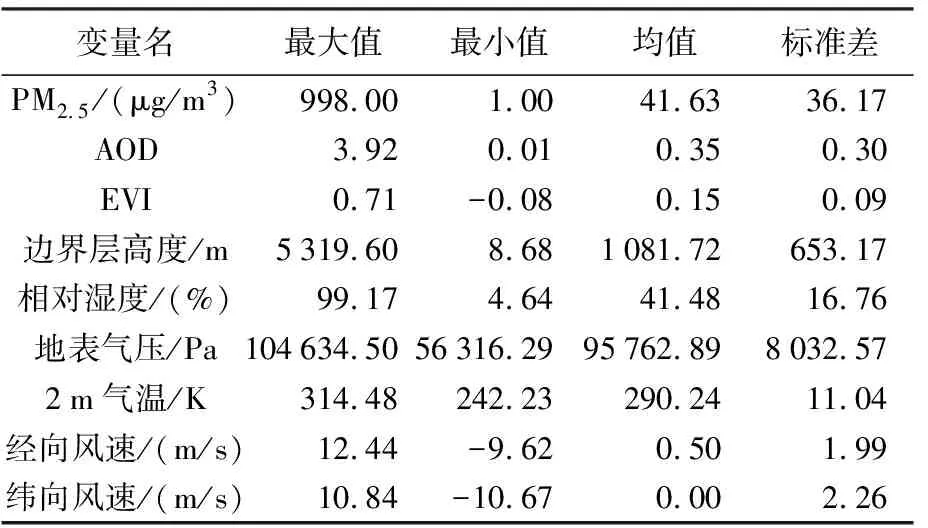
表1 近地表日均PM2.5浓度遥感制图样本数据统计信息
2.2 试验设计
为充分检验后验标准差约束下GWR模型的有效性,选择不同参数构建4类GWR模型,全面探究不确定性约束前后GWR模型精度表现。模型A,自适应类型带宽、Bisquare核函数及CV带宽择优指标;模型B,自适应类型带宽、Bisquare核函数及AICc带宽择优指标;模型C,固定类型带宽、Guassian核函数及CV带宽择优指标;模型D,固定类型带宽、Guassian核函数及AICc带宽择优指标。因条件数(condition number,CN)通常可用来诊断GWR估算结果的局部共线性问题[23],本文还进一步深入系统评估了GWR模型精度、奇异值甄别效果和回归系数正负比例随不同后验SD与CN阈值约束的敏感性。
GWR模型精度检验过程中,本文采用基于样本、站点及区域的3种十折交叉验证方法[24]。基于样本的交叉验证是指将本文中所有236 206个样本点的时空位置随机打乱分成十组,换言之,同一个PM2.5站点上的样本数据某些时刻可用于精度检验,某些时刻可用于建模。基于站点的交叉验证则是将1356个地面站点随机打乱分成十组,验证站点在所有时刻的样本全用于模型检验。基于区域的交叉验证是将省级行政区随机打乱分成十组,落在用于验证的省级行政区内所有站点在所有时刻的样本点均用于模型检验。模型精度检验指标采用拟合优度(coefficient of determination,R2)与均方根误差(root mean square error,RMSE)。
根据不确定性约束的敏感性分析结果,择优选择GWR模型与后验SD阈值实现地表PM2.5浓度制图,并对比不确定性约束前后制图结果,实证GWR建模结果不确定性度量与约束方法的有效性。
2.3 不确定性约束前GWR模型精度分析
图3中4类GWR模型带宽时间序列值对比可知,自适应型带宽优化结果对CV/AICc优化指标的选取并不敏感,模型A与模型B的带宽均值相近;但固定型带宽优化结果在不同优化指标的选取下相差较大,模型D的带宽均值明显低于模型C。与此同时,表2中不确定性约束前模型A与模型B的拟合、样本验证与站点验证精度明显优于模型C与模型D,说明采用自适应型带宽确保局部回归建模样本数量相同可有效提升GWR建模精度。但对于固定型带宽的模型C与模型D,因较低空间带宽易导致某些区域局部回归缺少充足建模样本,因此模型D预测结果常产生较多奇异值,使得总体拟合与验证精度严重偏低。不仅如此,表2中基于区域的交叉验证结果显示,4类GWR模型的区域验证R2与RMSE结果均不理想,表明未经不确定性约束的GWR模型预测结果可信度低。

图3 4类GWR模型带宽时间序列
2.4 不确定性约束下GWR模型的敏感性分析
2.4.1 模型精度稳定性分析
图4绘制了不同后验SD阈值约束下,GWR模型拟合及十折交叉验证的R2与RMSE结果,以及相应剔除率的变化情况。结果表明,4类GWR模型拟合、十折交叉验证RMSE随着后验SD阈值的降低而降低,后验SD约束可较好提升GWR模型精度。同时,除模型D外,其他3类GWR模型的拟合与十折交叉验证R2分别呈现出随后验SD阈值降低而下降和升高,且两者之间差异逐步变小的结果,一定程度上展现了后验SD约束在缓解GWR模型过拟合现象中的作用。相比较表2中约束前的拟合与验证结果,在后验SD阈值仅设为30 μg/m3时,4类GWR模型精度仍均有提高,且精度提升比例在模型D上尤为突出。模型D的拟合、样本验证、站点验证及区域验证结果分别仅在剔除0.56%、2.89%、2.96%及21.15%的样本后,RMSE提升比例分别可达92.99%、96.06%、97.10%及99.83%,说明未经后验SD约束的GWR预测结果中存在的少量奇异值严重影响了GWR模型总体精度。
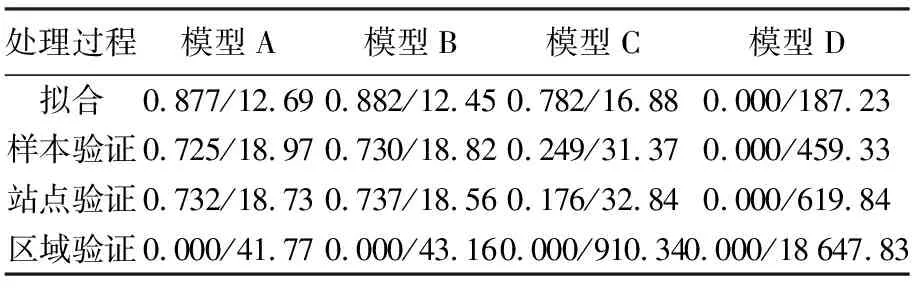
表2 后验SD与CN约束前各类GWR模型的拟合、样本验证、站点验证及区域验证的R2/RMSE
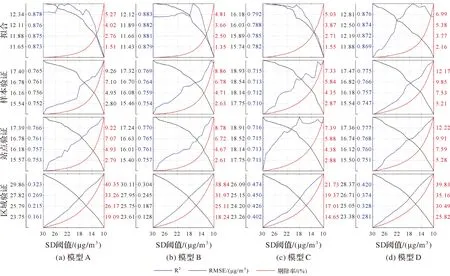
图4 不同后验标准差阈值约束下GWR模型拟合及十折交叉验证的R2、RMSE与剔除率统计
由图5中CN阈值约束结果可知,虽然GWR模型基于样本验证及站点验证的R2与RMSE结果随着CN阈值降低均分别呈现出上升及下降趋势,但拟合及基于区域验证的R2与RMSE结果却呈现相反的变化趋势。这一结果表明,传统CN阈值约束或许不是有效提升GWR模型精度的手段。此外因为过多样本剔除,即样本点偏少易导致R2与RMSE等指标计算不稳定。图5表明,当CN阈值由50降至5时,样本剔除率可由30%升至90%。
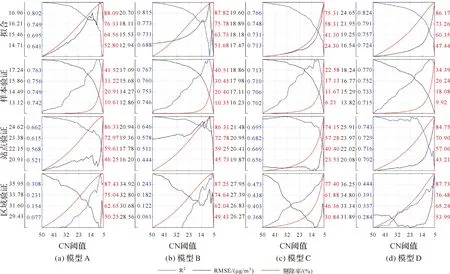
图5 不同条件数阈值约束下GWR模型拟合及十折交叉验证的RMSE与剔除率统计
2.4.2 奇异值甄别效果分析
图6与图7分别展示了采用自适应型带宽与固定型带宽的4类GWR模型拟合及交叉验证散点图,结果表明4类GWR模型的预测结果均存在奇异值,但采用自适应型带宽的GWR模型奇异值在量级与数量上均要小于采用固定型带宽的GWR模型。对于采用自适应型带宽的模型A与模型B,在地面站点PM2.5浓度较高时存在少量低估的GWR预测值,随着后验SD阈值从30 μg/m3降至10 μg/m3时,这些低估的预测值可被逐步剔除。对于采用固定型带宽的模型C与模型D,其GWR预测的奇异值却可达1500 μg/m3及-40 000 μg/m3,说明局部建模样本不充足是产生奇异值的主要原因。后验SD对甄别奇异值仍具有较好效果,当后验SD阈值降为10 μg/m3时奇异值均可被剔除。
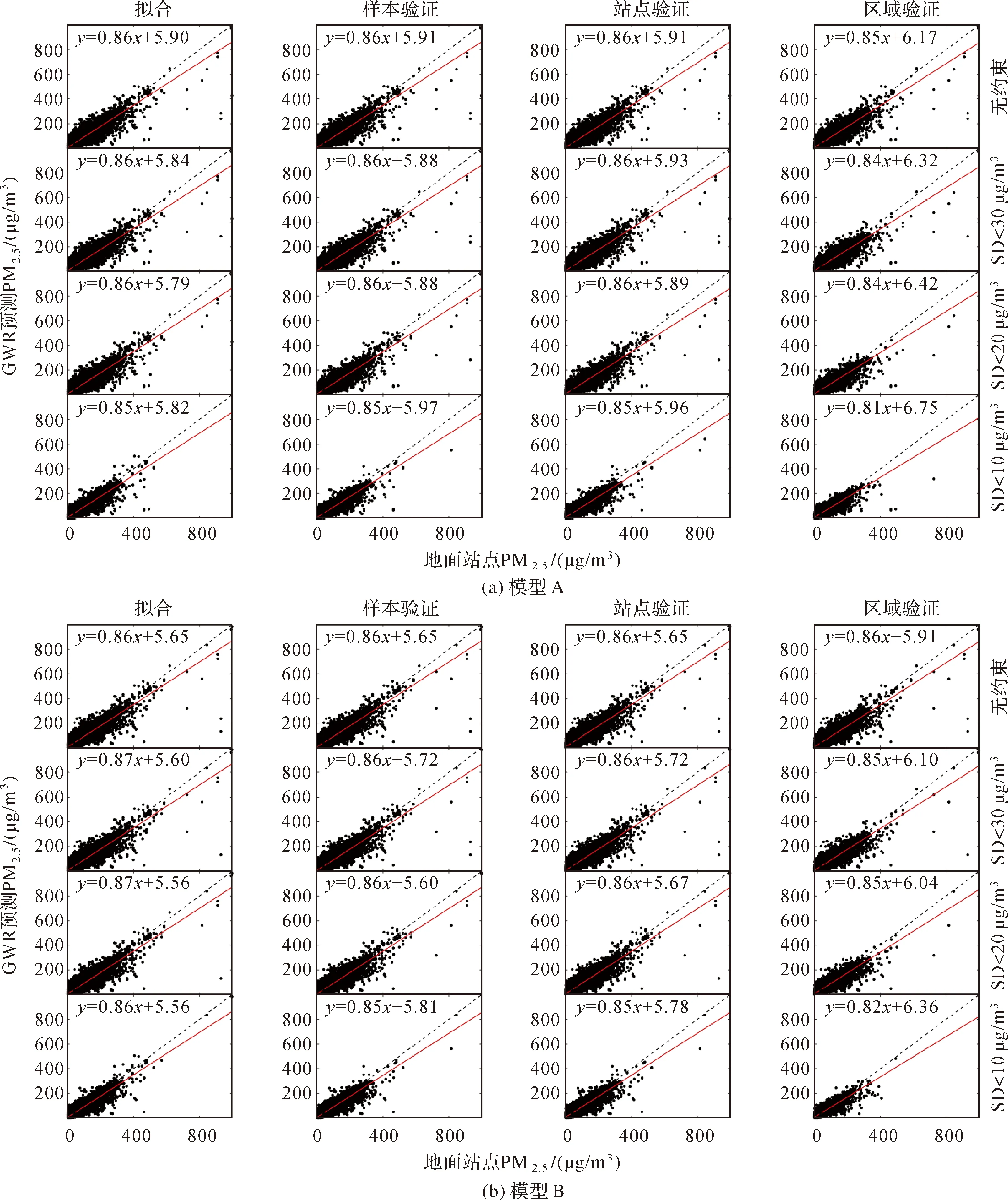
注:红实线为回归线,黑虚线为1∶1参考线。

注:红实线为回归线,黑虚线为1∶1参考线。
2.4.3 模型局部共线性优化
在地表PM2.5浓度建模制图过程中,由于建模变量在空间临近范围内常表现出较强的相似性,因此易发生局部共线性,进而导致GWR回归系数符号与实际情况存在偏离。图8显示了4类模型拟合结果在不同后验SD阈值/CN阈值约束下,符号为正的AOD回归系数与符号为负的EVI回归系数占总回归系数比例的变化趋势。由图8可知,随着后验SD阈值从30 μg/m3降至2 μg/m3时,4类GWR模型正符号的AOD回归系数比例提升范围分别为75.67%~82.11%、75.24%~78.60%、90.09%~94.12%与78.22%~85.34%,而负符号的EVI回归系数提升范围分别为62.51%~66.38%、62.44%~67.43%、71.99%~78.51%与62.73%~67.40%。与之类似,CN阈值约束结果同样呈现了相似规律,当CN阈值逐渐从100降低至10时,正符号的AOD回归系数比例与负符号的EVI回归系数比例也有所提升。这些改进结果更加符合PM2.5浓度地理要素作用机制,即在地表PM2.5浓度关联分析中,遥感AOD常呈现较强的正相关性[25],遥感EVI则因森林叶面可吸附并捕获PM2.5微粒常呈现负相关性[26]。综上可知,后验SD与CN约束均能缓解局部共线性带来的GWR建模过程中的系数符号偏离问题,但考虑图5中CN约束易导致过多样本被剔除,后验SD约束方案更加合理。
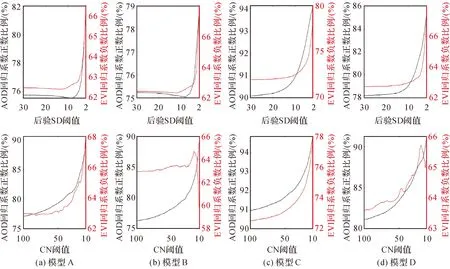
图8 不同后验SD阈值与CN阈值下,4类GWR模型拟合结果AOD系数正数比例趋势图与EVI系数负数比例趋势图
2.5 地表PM2.5浓度制图结果对比分析
在综合考虑4类GWR模型后验SD约束的建模效果基础上,本文设定后验SD阈值为10 μg/m3,基于模型B模拟生成了GWR模型约束前/后研究区地表PM2.5浓度。图9(a)、(b)分别为2019年2月6日与2019年9月25日Aqua卫星PM2.5浓度模拟制图结果。由图9可知,未经后验SD约束的PM2.5浓度GWR模拟估算结果中,监测站点稀疏的西藏地区部分区域PM2.5浓度均高于100 μg/m3,与西藏地区地势高且污染排放量极少的事实相违背;相比,后验SD约束后的PM2.5浓度则未出现这些奇异值。与此同时,图10也展示了后验SD约束前/后PM2.5浓度GWR模拟估算结果中负数比例的时间序列及其频数分布。图10表明,约束后不合理PM2.5浓度负值比例大幅度降低,负数比例频数分布由约束前多数天的5%~10%下降至了约束后的0%附近,春冬两季更为明显。此外,2019年站点PM2.5浓度年均值分布、后验SD约束后Terra/Aqua卫星PM2.5浓度GWR模拟估算的年均制图结果、及后验SD约束前后站点PM2.5浓度与GWR模拟估算制图结果偏差频数分布表明,后验SD约束后GWR模拟估算PM2.5浓度与地面站点PM2.5浓度偏差总体减小,污染分布空间特征识别基本一致,污染严重区域主要集中在华北平原、四川盆地及新疆塔克拉玛干沙漠区域。
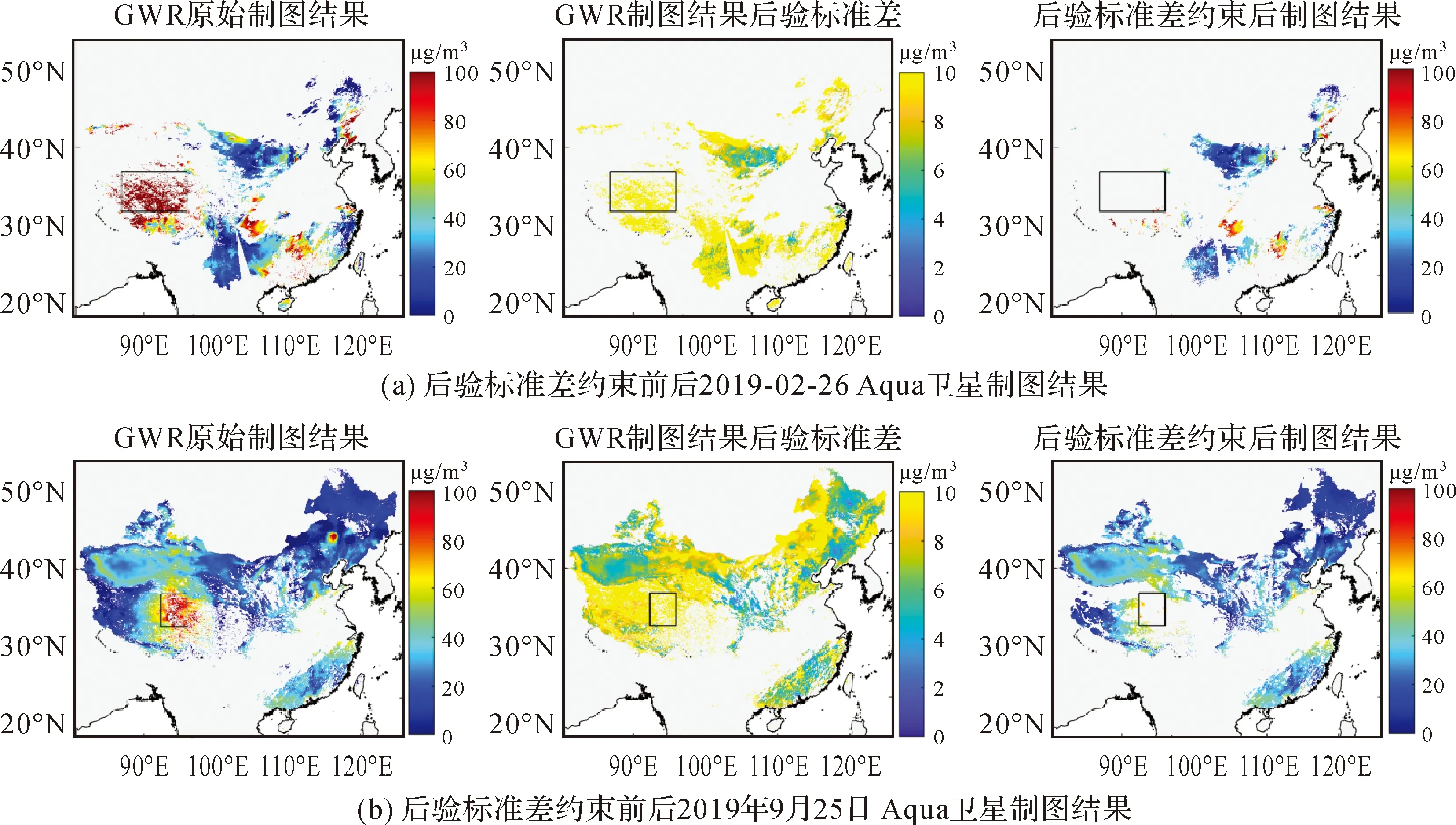
图9 2019年2月6日至2019年9月25日不确定约束前后地表PM2.5浓度制图结果

图10 不确定性约束前后地表PM2.5浓度制图结果中负数比例时间序列及其频数分布
3 总 结
针对样本空间稀疏程度及局部共线性等因素导致GWR模型精度呈现空间异质性的问题,本文提出了一种GWR建模结果不确定性度量与约束方法,并基于地表PM2.5浓度遥感制图案例对其进行了验证。结果表明,后验标准差约束下的GWR建模方法能有效甄别GWR模拟结果中的奇异值,提升模型的精度与模型模拟的可靠性。未来研究中,可进一步专注GWR建模中间过程,利用后验标准差约束GWR模型参数的训练(如空间带宽),直接获得更加稳健的GWR模拟估算结果。

