支持MEC的天地一体化网络下任务卸载和资源分配
李晓青 贺占权 周卫彤
1(航天恒星科技有限公司 北京 100095) 2(北京航空航天大学电子信息工程学院 北京 100191)
0 引 言
移动通信技术已经发展到第五代(5G),5G网络的主要工作频段为3 000~5 000 MHz,远远高于4G网络,这导致5G信号在信道中传播的衰减要更高。5G基站的覆盖半径仅为100~300 m左右,这为实现偏远地区用户以及海空中用户的组网覆盖提出了严重挑战[1]。近年来以小型化、低成本、低延迟和高吞吐量为特点的LEO卫星极大地促进了天地一体化网络(ISTN)的发展[2],ISTN已成为5G时代移动通信系统中一个必不可少的替代方案[3]。
考虑到5G时代偏远地区及海、空用户节点的组网需求,无法直接通过布置地面基站来完成全域覆盖,这使得ISTN朝着卫星可直连用户的方向发展;此外,用户设备(User Equipment, UE)侧流量急剧增长,而由于自身资源有限,UE在处理计算密集型和时间敏感型业务时能力不足的情况。为此,移动边缘计算(MEC)技术应运而生,相比于传统移动云计算(Mobile Cloud Computing,MCC)技术,MEC技术可以在更靠近UE侧配置,显著减少云端处理任务的时延。相比于传统蜂窝网络架构,ISTN架构的传播时延显著增加,天地链路变化频繁。随着服务的增多导致大量数据通过链路进行传输,大大增加了链路负载,给ISTN的网络架构设计带来严重挑战。使用MEC技术[4],将计算资源从云端分配至边缘服务器,能够极大地改善对用户的QoS,并且可以有效减少整个ISTN的流量。
在基于MEC的网络架构中,资源优化分配策略是研究热点。文献[5]考虑将多个独立用户的任务卸载到一个基站的蜂窝网络场景下,抽象为以时延和能量消耗最小化为目标的混合整数非线性优化(Mixed-Integer Nonlinear Programming, MINLP)问题,并设计了次优的算法来获得最优资源分配方案。文献[6]将拥有多个基站蜂窝网络划分为不同子区域,通过将多个独立计算任务卸载到MEC服务器或云端,对基站服务缓存和任务卸载进行联合决策以优化时延和能量消耗,基于Lyapunov优化和Gibbs采样对优化问题进行求解,提出一种次优的服务存储策略和任务卸载方案。文献[7]探讨ISTN场景下应用MEC技术来改善用户QoS的可行性,提出在近UE侧地面站和远端核心网地面网关布置MEC服务器,并提出一种协作计算卸载(Cooperative Computation Offloading, CCO)模型来实现天地一体化网络中多MEC服务器并行计算。文献[8]提出了一种在LEO卫星与近UE侧地面站布置MEC服务器的双边缘天地一体化网络,并提出基于双边缘ISTN中的协作分流方案,通过分析得出分流效率和能耗的性能。
上述文献普遍基于在拥有存储和计算能力的固定基站中配置MEC服务器,为UE缓存热点服务,并将用户的计算任务卸载至MEC服务器,将场景抽象成以服务缓存和任务卸载为决策,以最小化时延和能量消耗为目标的优化问题,并提出最优或次优的服务存储策略和任务分流方案。
本文考虑一种在LEO卫星上配置MEC服务器,直接与地面用户建立天地链路的ISTN架构,为地面基站无法覆盖到的区域提供MEC服务,大幅度提高偏远地区用户的QoS。基于串联排队理论得出ISTN场景的总时延成本,通过拉格朗日对偶理论和梯度下降法给出了ISTN网络的总传输时延成本的极小值,并基于模拟退火算法,提出任务卸载和资源分配联合调度方案,在多项式时间内给出近似全局最优的ISTN的时延成本。仿真结果表明本文算法相比于低复杂度启发式算法减少了20%的总时延成本,验证了ISTN下通过MEC技术保障地面用户QoS的可行性和有效性。
1 天地一体化网络模型
典型的ISTN包含地面网络与空间网络,具有规模庞大、支持的业务种类多、拓扑结构呈现立体多层次化和高动态变化的特点。
1.1 网络模型
本文考虑如图1所示的LEO卫星-UE双层天地一体化网络模型,将MEC服务器部署在LEO卫星上,为UE提供任务卸载服务。每个时隙内由MEC服务器决策是否为UE提供MEC服务以及LEO卫星为UE分配的带宽资源。
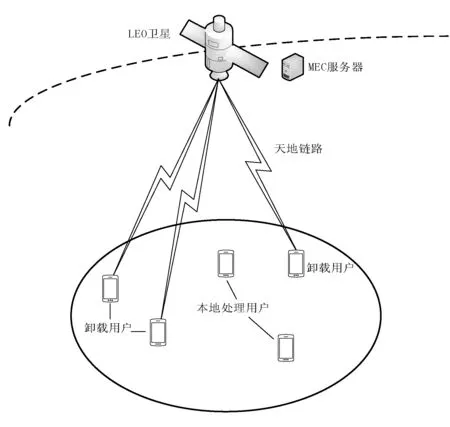
图1 ISTN架构
定义LEO卫星提供的通信能力为卫星提供的链路总带宽W(单位为Hz);提供的计算能力为MEC服务器中CPU的主频F(单位为Hz),MEC服务器的CPU可以处理用户卸载至LEO卫星的任务。
对于UE侧,定义UE集合为U={u1,u2,…,ui},UEui配置主频为fi的CPU以本地处理计算任务;ui产生的计算任务请求的CPU指令周期个数服从均值为ci(单位为CPU cycles)的负指数分布;计算任务的平均大小为di(单位为bits)。在时隙内ui上计算任务的产生是一个速率为λi的泊淞过程,在实际应用中,可以通过基于自回归模型等成熟的需求预测模型来估计时隙开始时的瞬时需求[10],使MEC服务器可以根据UE端设备的需求,为UE动态提供MEC服务。
传统的ISTN网络架构下进行任务卸载时,卫星通过用户链路、馈电链路为UE提供与远端核心网的链接,时延较长。本文设计的ISTN网络架构下,星上MEC服务器直接通过用户链路为用户提供MEC服务,无须通过馈电链路。在此架构上初步探究ISTN网络针对偏远地区用户及海空中用户的计算密集型任务的服务能力。
1.2 任务卸载和资源分配模型
假设每个UE的等效全向辐射功率(Equivalent Isotropically Radiated Power,EIRP)相同,LEO卫星采用正交频分复用(Frequency Division Multiple Access,FDMA)的接入方式,当不同用户共享频谱资源时不存在相互干扰。
MEC服务器进行任务卸载的决策有本地执行、完全卸载和部分卸载三种方案。本地执行即整个计算任务在UE本地完成;完全卸载即整个计算任务由MEC卸载和处理;为了简化分析,我们不考虑部分卸载的情况。则可定义一个二元决策变量ai={0,1}表示LEO卫星上的MEC服务器是否为UEui提供MEC服务。其中ai=1表示MEC服务器为ui提供MEC服务;ai=0表示ui在本地处理计算任务,则时隙内任务卸载决策是A={a1,a2,…,ai}。
整个LEO卫星可提供的总带宽为W,单位为bit/s,定义时隙内LEO卫星带宽资源分配决策B={b1,b2,…,bi},其中bi=[0,1],表示MEC服务器为ui分配的带宽占总带宽比例。因为本地计算的UE不占用频带资源,若ai=0,则bi=0,则用户链路通信速率Ri有:
Ri=biW
(1)
由于采用FDMA多址接入技术,所有UE分配的频谱资源不超过卫星的总通量,则ISTN的频带资源约束表示为:
(2)
1.3 时延模型
计算卸载的性能通常以时间延迟和能量消耗作为衡量指标。在ISTN场景下,我们主要关注MEC服务器在减小业务时延上的能力。ISTN下UE 产生的计算任务可以在本地执行或完全卸载,在本地执行时,时延成本是指在UE处执行本地计算所花费的时间,在完全卸载时,时延包括传输时延、传播时延、排队时延和计算时延。
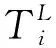
(3)
为了分析ISTN网络下计算任务完全卸载的时延成本,根据分组交换网络思想,可将整个网络建模成如图2所示的串联排队系统。
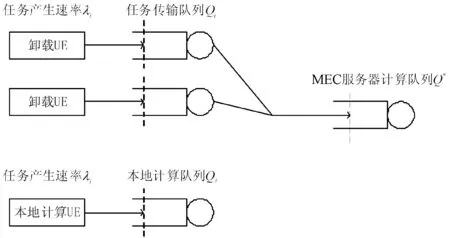
图2 串联排队系统
图2中队列集Q={Qi|∀ai≠0}是独立的M/D/1/FCFS队列,Qi表示卸载UE产生计算任务并上传LEO卫星的过程,Q是一个M/G/1/FCFS队列,表示MEC服务器处理计算任务的过程。队列Qi的服务时间ti为用户ui产生的计算任务的传输时延:
(4)
根据排队论的Pollaczek-Khinchin公式和Little定理任务有队列Qi的平均停留时间期望Ti为:
(5)
此时队列遵循稳态约束条件:
(6)
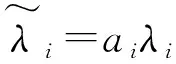
(7)
(8)
根据Pollaczek-Khinchin公式和Little定理有队列Q*的平均停留时间期望Ts为:
(9)
其中队列遵循稳态约束条件:
(10)
实际上,Pollaczek-Khinchin公式的稳态约束条件可理解为计算资源约束。由此,我们定义计算任务卸载至MEC服务器处理的时延成本为:
(11)
式中:Tsi(bi)是ui与LEO卫星的链路传输时延;Ts(A)是计算在LEO卫星上的平均停留时间;tc表示UE与LEO卫星之间的链路传播时延,由于我们忽略不同UE与LEO的距离变化,因此对于每个UE,tc是常数。
为了分析ISTN下用户QoS保障的问题,定义ISTN的总时延成本为:
(12)
其表示ISTN网络场景下MEC服务器减小UE时延成本的能力。
1.4 优化问题模型
优化问题的目标是制定任务卸载决策A和带宽资源分配决策B,以最大限度地减少总时延成本T(A,B)。优化问题P1的模型为:
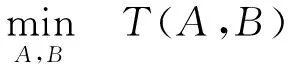
(13)
(14)
(15)
(16)
式(14)是计算任务上传队列稳定约束条件,代表LEO卫星在每个时隙内为UE分配的带宽应使计算任务上传队列稳定;式(15)是ISTN的带宽资源约束条件;式(16)是MEC服务器的M/G/1队列稳态约束,也可将其理解为MEC服务器的计算资源上限。
可以很容易地注意到,P1是一个MINLP问题,且优化函数非凸,这使得P1非常难以求解;另一方面,对于整数规划问题,通过穷举法得出最优的任务卸载决策A的时间复杂度为O(2N),这是一个指数级复杂度,并且对于每个卸载决策,都需要确定最佳的带宽分配。 由于算法的复杂性较高,在实际应用中是不可行的。
2 ISTN场景下任务卸载和资源配置方案
本文基于模拟退火算法和梯度下降法提出一种天地一体化网络任务卸载和资源分配(Satellite-Terrestrial Task Offloading and Resource Allocation,ST-TORA)方案。对于如何求解P1,首先考虑将A和B解耦,选定部分UE进行任务卸载,确定卸载决策向量A,将原问题松弛并根据拉格朗日法求解,得到带宽配置方案B和天地一体化网络总时延开销T(A,B)。然后基于模拟退火算法迭代更新决策变量A直到找到P1的局部最优解,将算法的时间复杂度降为多项式时间。
2.1 资源分配(RA)方案
当MEC服务器为多个UE提供MEC服务时,如何有效地将LEO卫星有限的带宽资源分配给卸载UE是本节要解决的问题。取ki=λidi/Φ,Ki=di/2Φ,队列Qi的平均服务时间为:
(17)
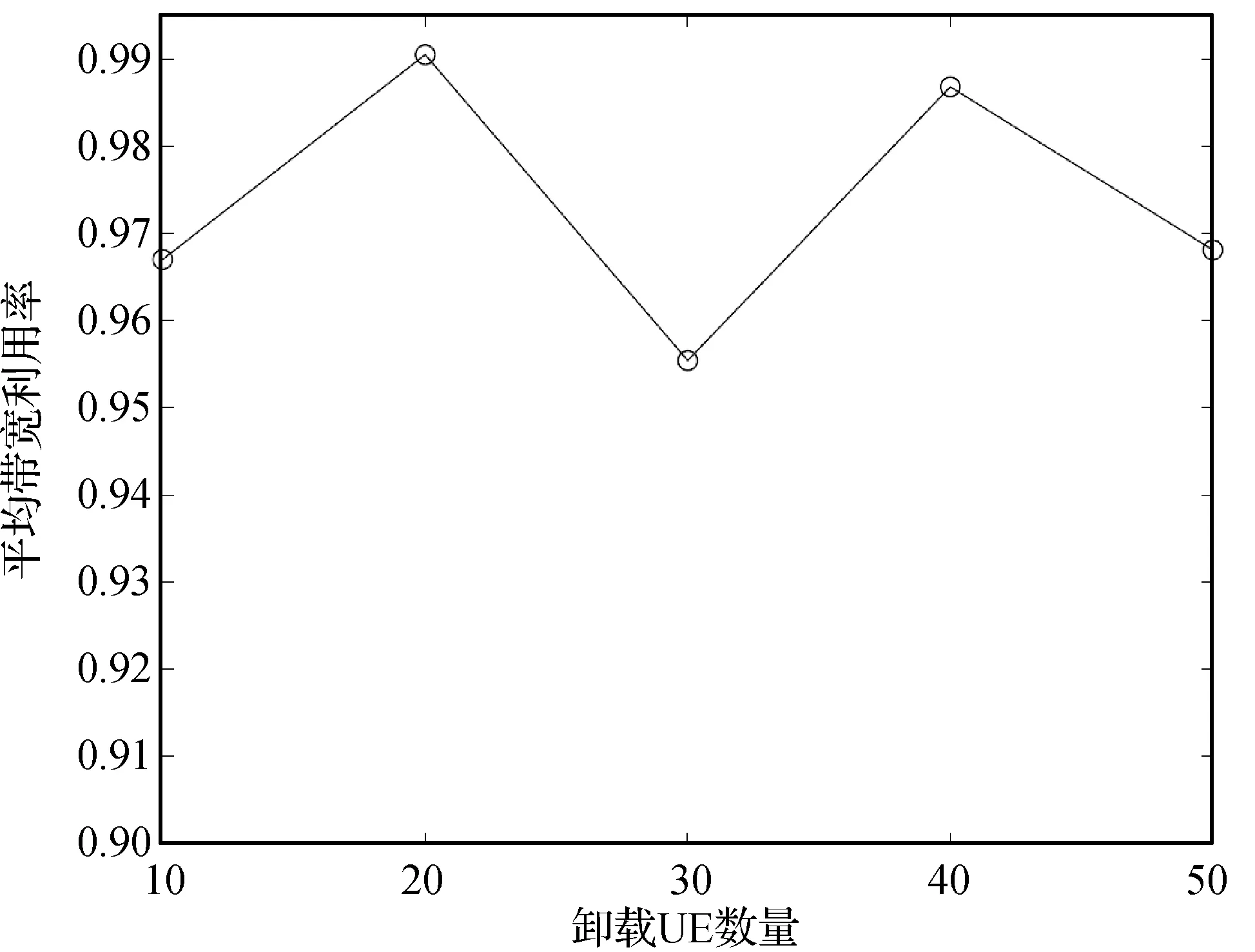
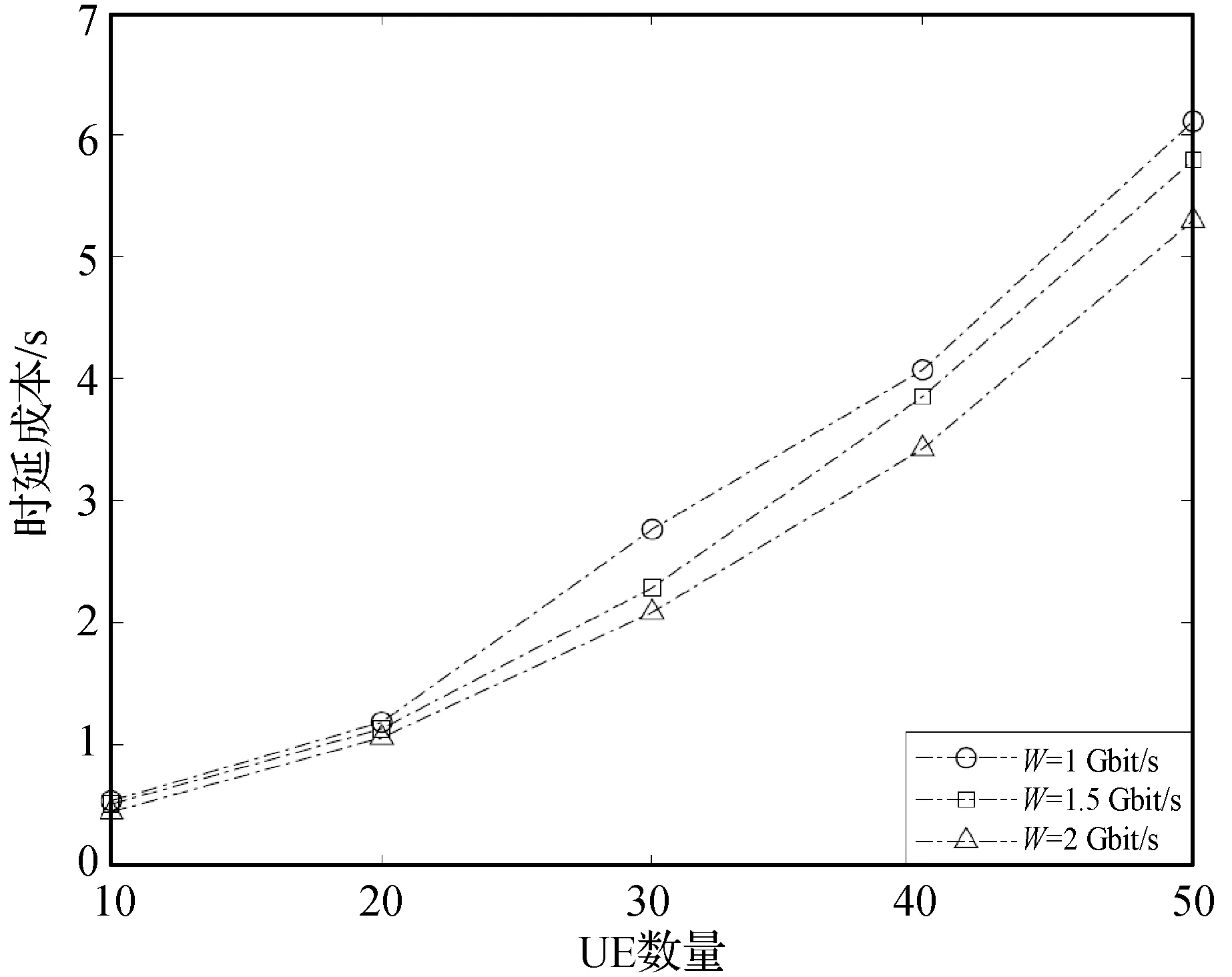
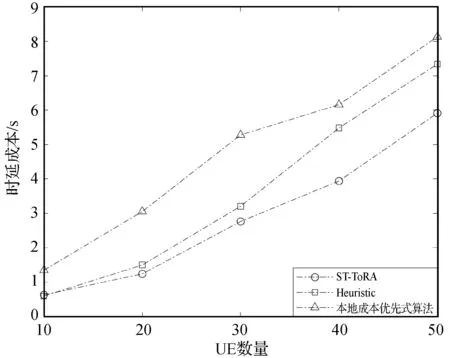
式中:ki代表了传输队列Qi稳定所需要分配最小带宽资源比例,当bi (18) s.t.bi>ki,∀bi≠0 (19) (20) 定理问题P2在满足约束条件下是一个凸优化问题。 证明式(19)的Hessian矩阵为: (21) 其中: (22) (23) 根据次梯度法得到拉格朗日乘子的迭代公式为: [εi(n)-m(bi-ki)]+ (24) (25) 式中:[x]+=max{0,x};n表示迭代次数;m表示迭代步长,应取足够小的正数。令: (26) 通过梯度下降法求解带宽分配的迭代公式为: (27) 当迭代步长小于最小迭代步长δ时迭代停止。因此当确定任务卸载决策A时,资源分配(Resource Allocation,RA)算法描述如算法1所示。 算法1RA 算法 输入:A,ki,Ki,I,W,F,tc。 输出:B,T。 初始化m,n,δ,,εi(0),μ(0),bi(0); n=n+1; endwhile 计算T(A,B); returnB,T 在任务卸载场景下,不同的UE业务有着不同的计算任务大小,RA算法可以为计算任务更大的UE分配更多的带宽资源,最小化网络场景下的传输时延成本。 任务卸载决策A的求解是一个整数规划问题,由穷举法寻找A的最优解的时间复杂度为O(2N),为指数级复杂度。可以预见,MEC服务器应优先为业务数据量更大、请求计算资源更多、计算资源更少的UE提供MEC服务,这意味着最优解附近的解也相对较优,适用于整数规划中的模拟退火算法。本文基于模拟退火算法,在多项式时间内寻找问题P1的近似全局最优值。 首先确定一个满足约束条件的初始任务卸载决策A,并通过RA算法得到B和T。之后对任务卸载决策向量A进行N*次如算法2所示的随机扰动得到Anew,通过RA算法得到Bnew和Tnew。其中N*为邻域解空间大小。 算法2disturb 算法 输入:A,I,W,F。 输出:Anew。 随机选取扰动UEi; chosen=rand; ifchosen≤0.6 ai=1; else ifchosen≤0.85 ||A中所有元素相等 随机选取与UEi卸载决策不同的UEj; ai=1-ai,aj=1-aj; else ai=0; returnAnew 令Δ=Tnew-T。若Δ<0则接受该结果;否则将有概率接受这个结果,概率计算公式为P=exp(Δ/τ),其中τ为当前温度,初始值设置为用户总数量。更新τnew=ατ,其中α为温度下降率。然后重新开始迭代,直到温度τ到达温度下界τmin,其中τmin设为一个足够小的正数。基于此,本文提出ST-TORA算法如算法3所示。 算法3ST-TORA 算法 输入:ci,di,λi,fi,I,W,F,tc。 输出:A,B,T。 [B,T]=RA(A,ki,Ki,I,W,F,tc); Whileτ>τmin fori=1:N*; Anew=disturb(A,W,F); [Bnew,Tnew]=RA(Anew,ki,Ki,I,W,F,tc); Δ=Tnew-T,P=exp(Δ/τ); ifΔ<0‖P>rand A=Anew; B=Bnew; T=Tnew; end if end for τ=ατ; end while returnA,B,T ST-TORA算法的时间复杂度取决于邻域解空间个数大小以及温度下降率,对于N位向量A,取N*=τ=N,ST-TORA算法的时间复杂度为O(NlogN)[12]。相比于穷举法,ST-TORA算法可在多项式时间内趋于全局最优。 在本节中,通过仿真对本文提出的ST-TORA算法进行验证,仿真结果表明了应用于天地一体化网络场景,在LEO卫星上部署MEC服务器,为UE提供边缘计算服务,以保障网络QoS的可行性及有效性。 考虑由单个LEO卫星和UE构成的天地一体化网络场景,通过在LEO卫星部署MEC服务器为UE提供边缘计算服务。其中每个UE的计算任务数据平均大小di,所需CPU转数ci,UE端CPU计算能力fi以及任务产生速率λi均随机生成,其中任务平均大小di与所需CPU转数ci呈线性相关。其中仿真平台配置为:Intel(R) Core(TM)i5- 4210H CPU @2.90 GHz;8 GB RAM;硬盘1 TB;Windows 10 Education 64位。在MATLAB 2020a环境下进行仿真,仿真参数如表1所示。 表1 ISTN场景仿真参数 3.2.1资源分配(RA)算法 图3所示为相同任务卸载决策下,本文基于梯度下降法设计的RA方案与带宽资源平均分配(Equal Bandwidth,EB)方案下,LEO卫星提供边缘计算的时延成本T与卸载用户数量的关系,其中LEO卫星总通量W为1 Gbit/s,MEC服务器的CPU主频F为10 GHz。 图3 卸载时延与卸载UE数量关系 可以看出,随着卸载UE数量的增多,RA算法按业务需求量分配带宽的优势更加明显。当任务卸载决策确定时,计算任务在MEC服务器的总停留时间的期望Ts(A)确定,RA算法可动态地为业务需求高的UE分配更高的带宽资源,避免带宽资源浪费并最小化总时延成本。 图4给出了LEO卫星总通量W为1 Gbit/s,MEC服务器的CPU主频F为10 GHz的场景下,RA算法的平均带宽利用率与卸载UE数量的关系。平均带宽利用率定义为五十次仿真下带宽分配向量B中各元素之和的平均值。 图4 平均带宽利用率与卸载UE数量关系 RA算法的性能由每次迭代的步长m以及拉格朗日乘子εi和μ的初值决定,若步长m过大则可能越过极值点,m过小则算法收敛时间过慢;而拉格朗日乘子会随着迭代次数的增加而逐渐收敛。由图4可以看出,在带宽利用率保持在0.95以上的同时,RA算法可以很好地逼近目标函数的极小值。 3.2.2ST-TORA算法 图5给出ST-TORA算法下3种总通量的LEO卫星进行任务卸载的时延成本与UE总数量的关系。MEC服务器的CPU主频F设置为10 GHz。 图5 不同总通量下时延成本与UE数量关系 可以看出天地一体化网络场景下时延成本与卫星的总通量直接相关,这是因为卫星总通量的增长直接减少计算任务的传输时延,大大保障UE端的QoS。随着UE数量的增长,每0.5 Gbit/s的通量增长可为UE侧减少100 ms的传输时延。随着卫星通信技术的不断进步,超低轨道高通量卫星提供的总通量可高达100 Gbit/s级,传输时延可缩短至μs级;而相同通量下,LEO卫星可提供的覆盖性远高于地面基站。 图6给出了ST-TORA算法下3种计算能力的MEC服务器进行任务卸载的UE卸载比例与UE总数量的关系。LEO卫星提供的总通量W设置为1 Gbit/s。 可以看出,卸载UE比例是MEC计算能力的一个递增函数。由于计算资源约束条件的存在,MEC服务器的CPU主频越高,计算任务在MEC服务器的总停留时间越短,MEC服务器可为更多的UE提供服务。当UE总数量较少时,天地一体化网络中LEO卫星可以提供足够的计算资源和带宽资源时,所有UE可以将计算任务上传至MEC服务器;随着UE数量的增多,由于MEC服务器的计算资源和LEO卫星提供的带宽资源有限,相同UE总数量下卸载UE个数会趋于一个稳定值。 图7 不同算法下时延成本与UE数量关系 表2 不同算法收敛时间对比 单位:s 由图7可以看出,由于为过多的UE提供了MEC计算服务,LEO卫星为每个用户分配的带宽资源只能勉强维持传输队列稳定,因此本地成本优先式算法的性能最差。随着UE数量的增多,相比于低复杂度的Heuristic 算法的时延成本,本文所提ST-TORA 算法的时延成本可降低约20%。两种算法同样基于启发式算法,但基于模拟退火思想的ST-TORA算法可以跳出局部最优解达到全局最优解。但由表2可以看出ST-TORA算法的收敛时间要高于Heuristic算法,这是因为模拟退火算法的时间复杂度受温度下降率以及温度下界的直接影响,在本文仿真场景参数下,为了保证算法在减小时延成本方面的优越性,ST-TORA算法的时间复杂度高于Heuristic算法。 本文研究支持MEC 的天地一体化网络场景下任务卸载和资源分配联合优化方案。首先建立了LEO卫星(边缘网络)-UE的双层ISTN模型;然后通过排队论与分组交换网络的思想对模型的时延成本进行考察,并最终将降低时延成本的过程抽象为一个MINLP问题,本文将其转为2个子问题进行求解:(1) 为最小化计算任务卸载至部署了MEC服务器的LEO卫星的传输时延成本,基于拉格朗日乘数法和梯度下降法,为每个UE分配最优的带宽资源。(2) 基于模拟退火算法,降低整数优化的时间复杂度,寻找到逼近最优的联合任务卸载和资源分配方案。仿真结果表明本文算法能够更好地满足天地一体化网络下的需求,有效降低其时延成本。下一步的工作考虑引入核心网-LEO-UE三层模型的缓存网络场景[14],进一步优化天地一体化网络下UE的QoS。2.2 任务卸载决策
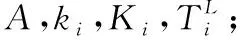
3 仿 真
3.1 仿真场景及参数设置

3.2 仿真结果及分析

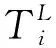

4 结 语

