基于MATLAB的重力式挡土墙可靠度计算程序开发及其应用
宋云连 付 宇 李 强,2
1(内蒙古工业大学内蒙古自治区土木工程结构与力学重点实验室 内蒙古 呼和浩特 010051) 2(郑州市市政工程总公司 河南 郑州 450001)
0 引 言
重力式挡土墙因其结构简单、施工简便、可就地取材等特点被广泛应用。当前的挡土墙稳定性分析和验算软件以安全系数法为主流,尽管该方法是一种相对有效的工程实用法,因其未考虑参数的不确定性,在实际工程中会出现安全系数的大小和工程结构的安全程度不匹配的现象[1]。为此,将以概率论为基础的可靠度理论引入到挡土墙稳定性分析,国内外已有一定的研究成果。杜永峰等[2]以一重力式挡土墙为例,采用JC法对挡土墙的两种主要失效模式进行计算,并用串联理论进行系统靠度分析。王海祥等[3]采用蒙特卡罗法对重力式挡土墙的抗倾覆和抗滑移稳定性进行分析计算并与定值分析法进行比较,得出某些挡土墙安全系数足够,而投入使用却发生破坏的结论。Low[4]采用一次二阶矩法在考虑挡土墙参数正态和非正态分布基础上对挡土墙的计算进行程序设计,并将其与Excel相结合使计算过程更加简化明了。Castillo等[5]将传统安全系数法与概率理论方法相结合计算出重力式挡土墙的失效概率,并对其进行敏感性分析和计算过程的优化设计。Sivakumar等[6]采用可靠度理论对影响悬臂式挡土墙稳定性的不确定参数随机模拟,确定了抗滑移、抗倾覆等可靠指标和失效概率的取值范围。
综上所述,以定值理论为基础的挡土墙分析软件已经不能满足实际工程需求;将可靠度引入挡土墙稳定性分析恰好可以弥补定值计算的缺陷,且该方法已经具备一定的理论支撑。此外,因挡土墙可靠度分析涉及复杂方程且运算量极大,需辅以计算机。查阅计算机软件类文献发现,MATLAB的高效算法及其完善的GUI窗口开发功能与该法的需求不谋而合[7-12]。因此,本文以蒙特卡罗法为基础,结合MATLAB的GUI功能,开发出一款面向对象的重力式挡土墙可靠度计算和敏感性分析的通用计算程序软件。该软件具备在重力式挡土墙尺寸、墙后边坡参数及墙后填土随机参数已知的条件下,可直接计算出重力式挡土墙抗倾覆和抗滑移的失效概率与可靠指标,并绘制随机变量参数的敏感性分析曲线图。此外,该软件也具备定值计算的功能,可以求解抗倾覆和抗滑移安全系数。
1 重力式挡土墙模型及其功能函数的建立
1.1 挡土墙通用计算模型建立
对挡土墙的稳定性进行分析计算的前提是建立挡墙通用模型,如图1所示。
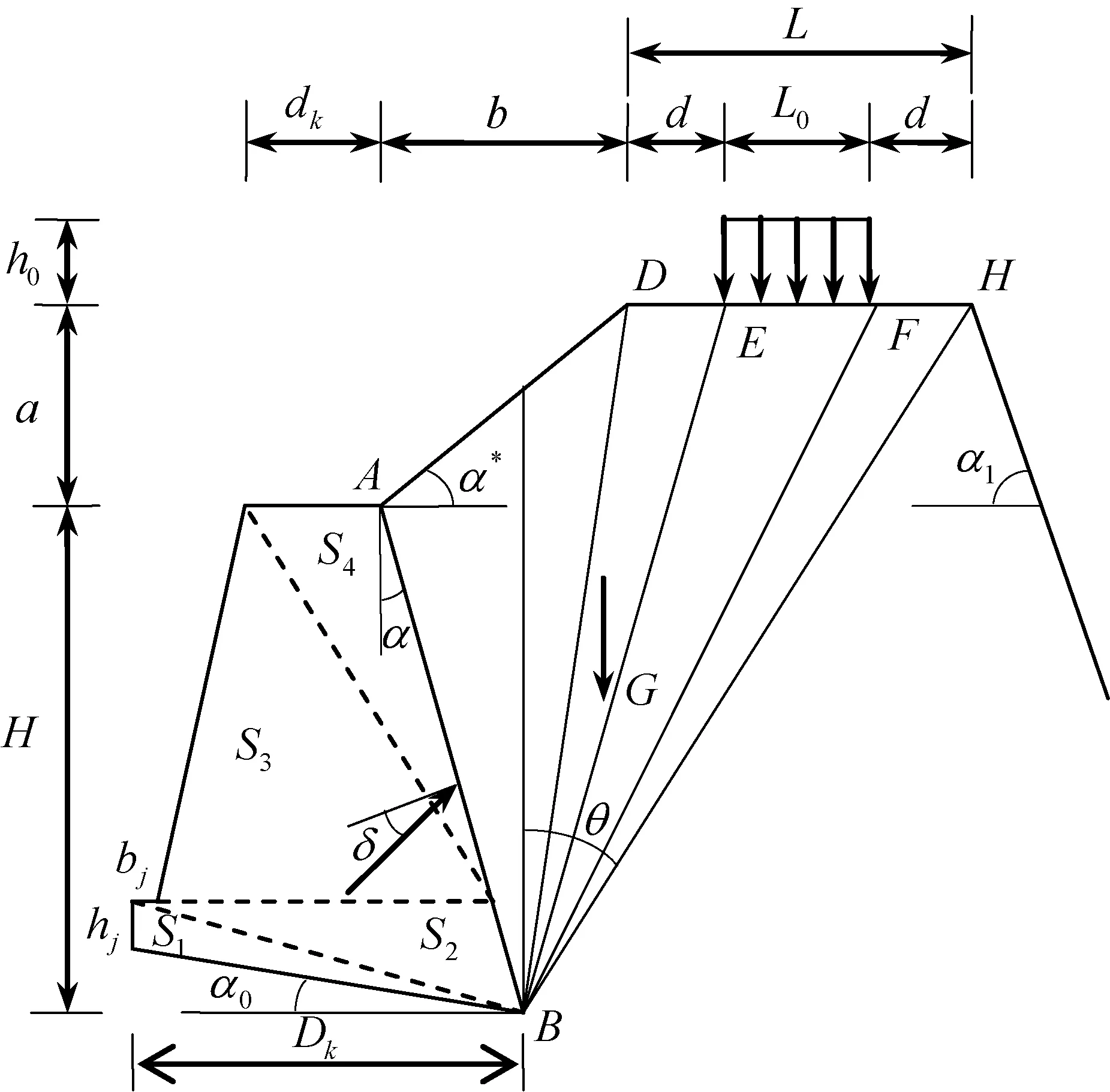
图1 重力式挡土墙通用模型
该模型的主要参数有:挡土墙自身尺寸参数(高度H、顶宽dk、底宽Dk、墙背倾角α、墙趾高度hj、墙趾宽度bj、墙底倾角a0);填料参数(填料容重γ、均值γmu、标准差γsig;填土内摩擦角均值φmu、标准差φsig;填土与墙背间内摩擦角δ、均值δmu、标准差δsig);墙后边坡参数(墙顶与路面高程差a、内边坡斜率α*、路肩宽b、行车道宽度L0、外边坡斜率α1)。
1.2 挡土墙自身截面面积及重心计算
为简化挡土墙截面面积及其重心力矩的公式推导,现将图1中的挡土墙分为固定的四个三角形模块,经过推导每一模块的面积计算公式如下:
S1=0.5×Dk×hj
(1)
S2=0.5×[(hj+Dk×tana0)×tana+Dk]×
(hj+Dk×tana0)
(2)
S3=0.5×[(hj+Dk×tana0)×tana+Dk-bj]×
(H-hj-Dk×tana0)
(3)
S4=0.5×dk(H-hj-Dk×tana0)
(4)
经推导各模块重心距离墙趾的距离为:
l1=Dk/3
(5)
l2=[(hj+Dk×tana0)×tana+2×Dk]/3
(6)
l3=[(hj+Dk×tana0)×tana+Dk+2×bj+
(H-hj-Dk×tana0)×tana]/3
(7)
l4=[(hj+Dk×tana0)×tana+2×
(H-hj-Dk×tana0)×tana+Dk+dk]/3
(8)
式中:墙背俯斜时α为负值,仰斜时α为正值。经计算可得重力式挡土墙的截面面积为:
S=S1+S2+S3+S4
(9)
其自重重心距墙趾的距离为:
l=(l1+l2+l3+l4)/2
(10)
1.3 最大主动土压力及其作用点计算
在程序设计过程中,挡土墙墙后主动土压力计算采用库仑土压力理论。假设墙后填土破裂面为直线型,取单位长度的挡土墙墙后破裂棱体,利用力多边形和正弦定理求得墙后主动土压力Ea的表达式如下[13]:
(11)
式中:Θ=a+δ+φ,α和δ角度的含义见图1;G=γS为破裂棱体单位长度上的自重。破裂棱体横断面的面积可以表示为:
S=A0tanθ-B0
(12)
式中:A0和B0是用来表示不同破裂棱体横断面的参数。由于破裂角θ交与位置不同时(如交于内边坡,路面上荷载内部、中部及外部),只有单位长破裂棱体自重G的表达式不同,当破裂棱体采用同一种土质修筑时,G的不同之处表现在破裂棱体横断面面积S的不同。利用软件计算S时,其破裂面的搜索范围为0到90度,搜索步长为0.01度。根据破裂面交于位置不同,各部位S中的主要参数及其作用点的计算公式如表1,各边界条件的判定则是依据图1中尺寸参数求出临界破裂角θ的正切值。
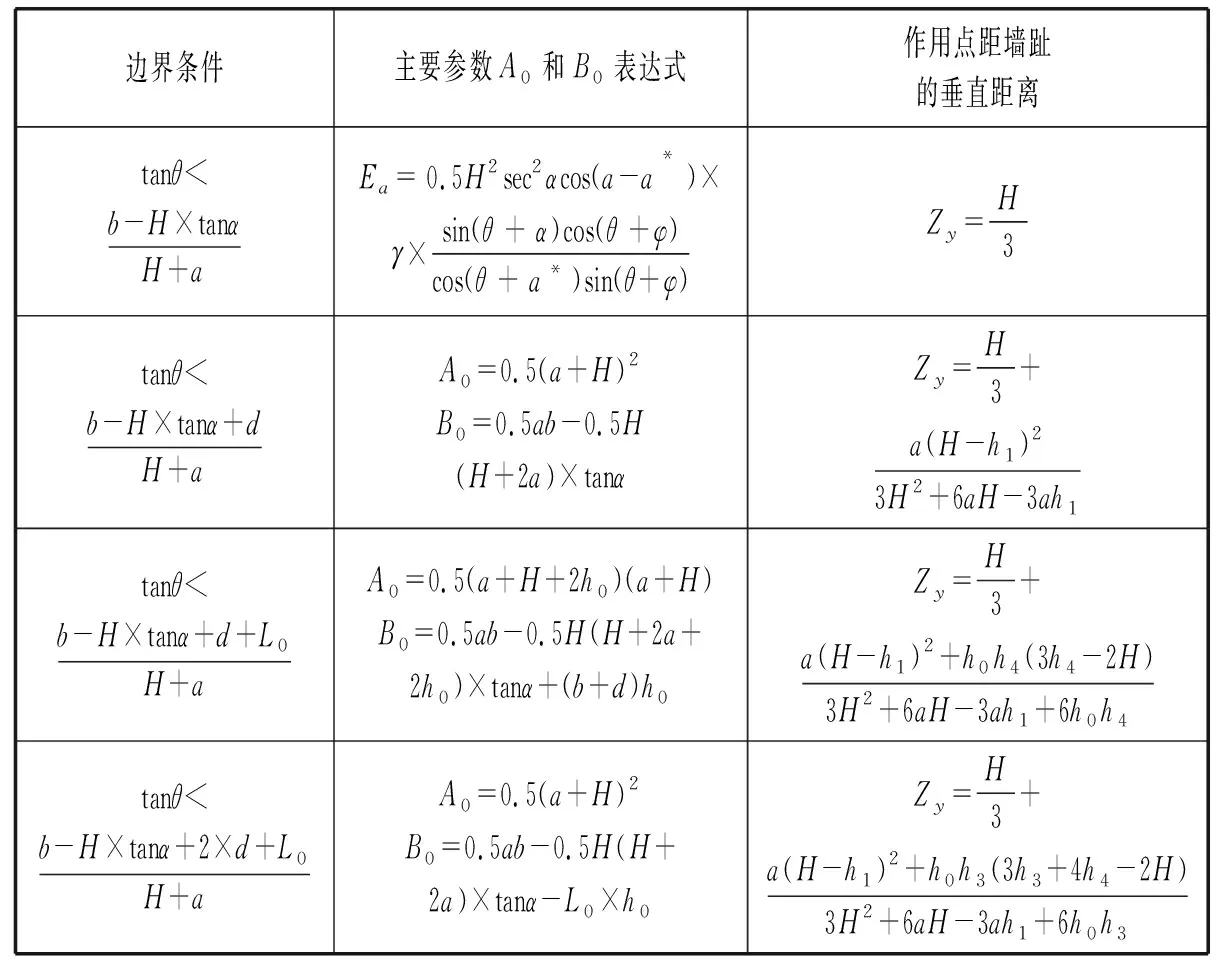
表1 不同边界条件对应主动土压力主要参数计算公式
表1中,h1=(b-a×tanθ)/(tanθ+tanα),h2=d/(tanθ+tanα),h3=L0/(tanθ+tanα),h4=H-h1-h2-h3。其中,Zy为各部位对应的垂直作用点距离,水平力矩Zx=Dk-Zy×tanα。
在计算出破裂面交于各部位的所有主动土压力后,通过语句Eamax=max(Ea)找到最大主动土压力及其对应破裂面,进而通过查找语句追溯Eamax对应的破裂角及相应的作用点力矩大小。
1.4 可靠度计算功能函数的建立
(1) 抗滑移稳定性功能函数。重力式挡土墙抗滑移稳定性设计要求基底摩阻力大于挡墙的滑动力。借助抗滑移安全系数定义,建立其抗滑功能函数表达式:
Z1=Mr-Ms=(Gy+Ex)μ-(Ey-Gx)=
(G×cosa0+Ea×sina0)μ-(Ea×cosa0-G×sina0)
(13)
式中:G为挡墙自重;Ea为最大主动土压力;Gy为垂直于基底的挡墙自重分力;μ为基底摩擦系数。
(2) 抗倾覆稳定性功能函数。借助挡土墙抗倾覆安全系数定义可建立重力式挡土墙抗倾覆功能函数为:
Z2=Fr-Fs=GZG+EyZx-ExZy=
GZG+Ea×cosa0×Zx-Ea×sina0×Zy
(14)
式中:Zx和Zy分别为最大主动土压力作用点距墙趾的横向和纵向力矩。
2 软件可视化界面设计及程序编写
2.1 用户界面设计
在MATLAB的命令行窗口输入guide即可启动GUIDE工具。在该环境下,运用Edit Text、Static Text、Push Button、Pop-up menu、Panel等控件设计出挡土墙计算的主界面窗口及各子界面窗口上的参数输入、模型图输出及条件选择等对话窗口[14]。各界面的菜单栏则采用Menu Editor控件设计,主界面布局见图2。
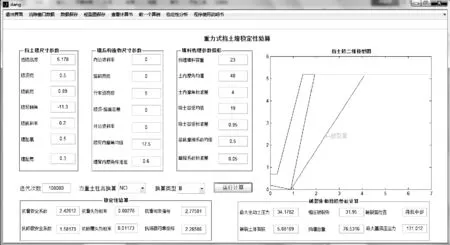
图2 主界面架构
图2中左上部分是已知信息输入界面;左下部分是结构可靠度和失效概论以及安全系数的计算结果输出界面;右上是供挡墙计算图形输出预留的界面;右下部分是挡土墙计算过程中的中间结果输出界面。本程序软件还可以根据需要对界面进行任意的预留或者输出界面设计。
主子界面之间的切换则采用MATLAB中的“set (gcf,′visible′,′on′) 子界面名称”语句来实现,而不同界面上数据的传递处理方法则是以两界面间所需所有变量转化为全局变量“Global 变量名”的形式实现的。
2.2 程序代码编写
在设计出界面对话窗口后,可运行GUI界面生成各个界面主程序框架,实现功能的代码即可嵌入在该框架下的主函数或者各控件的回调函数架构中。然后通过类似str2num(get(handles.编辑框编号,′string′))的get语句获取控件的输入信息。在读取所需参数后,按照重力式挡土墙可靠度计算流程进行相应的程序代码编辑。首先,由各随机参数的均值和标准差用normrnd(均值,标准差,M,N)语句生成M行N列服从正态分布的随机矩阵。然后依据表1中计算公式,依次编写出各边界条件下主动土压力Ea计算程序,最后通过以下搜索方法找到最大主动土压力:
j=0;
while (j j=j+1; if Eamax==Ea(j) break; end end w1=(j-1)/100+aaf % aaf为最大Ea对应破裂角 挡土墙二维模型图绘制方法是将挡墙模型主要转折点的二维坐标通过“plot([X,Y]”语句连接,随后通过“hold on”语句将所有关键点连线绘制到同一幅坐标图中。最后,运用类似“set(handles.fig1)”的set语句可将模型图以及运算结果输出到GUI界面的指定区域[15]。挡土墙结构抗滑和抗倾覆可靠度计算的具体程序流程设计框图如图3所示。 图3 程序计算框图 挡土墙界面设计和各界面所需所有程序编写完成后,界面上的输入参数、程序中间计算过程数据(主动土压力力矩、挡墙重心力矩、换算土柱高度等)和计算结果的保存可结合Excel表格实现。设计思路为:首先在计算机指定文件夹(如D:1
etaining)中建立一个Excel空表格(如retaining.xlsx),然后由:“xlswrite(′D:1
etaining
etaining.xlsx′,*,′Sheet1′,′I19′)”语句,将参数保存到该指定目录下retaining.xlsx文件中相应的工作表(Sheet1)中的预设位置(I19)。 界面上的曲线分析图与挡土墙模型图可采用以下语句存为JPG图片。 axes(handles.*); newfig=Fig. ; set(newfig,′visible′,′off′); set(newfig,′color′,′w′); newaxes=copyobj(handles.fig1,newfig); set(newaxes,′Units′,′default′,′Position′,′default′); [filename, pathname]=uiputfile({′*.jpg′, ′Fig.type(*.jpg)′},′储存图片′); if isequal(filename,0)||isequal(pathname,0) return end str=fullfile(pathname,filename); f=getframe(newfig); f=frame2im(f); imwrite(f,str); close(newfig) 若要查看详细的计算数据只需点击GUI界面菜单栏中的“查看计算书”按钮即可打开保存有计算过程及计算结果的Excel表格,该功能由MATLAB语句“winopen(′D:1
etaining
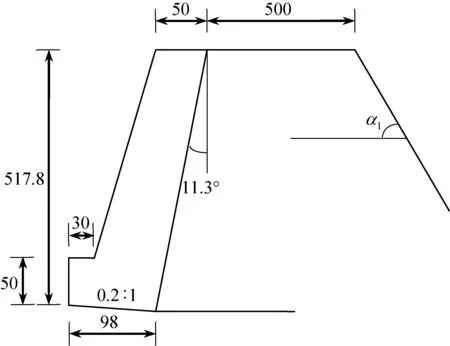
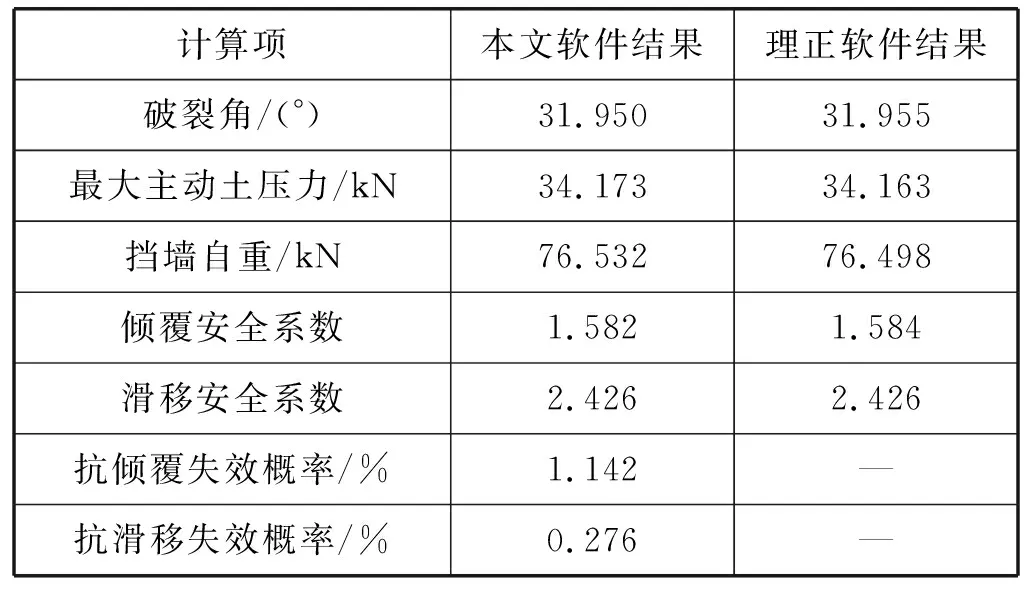
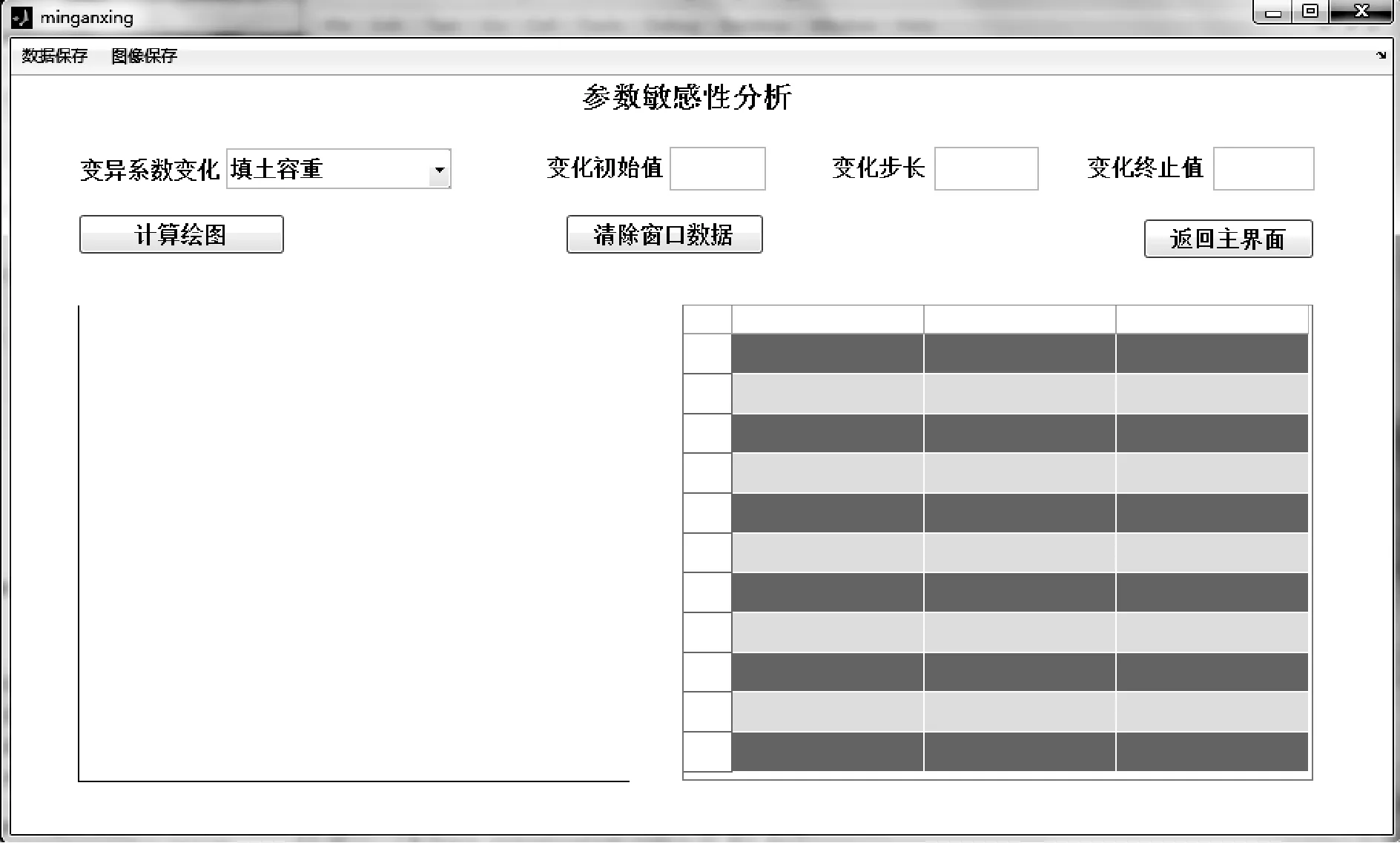
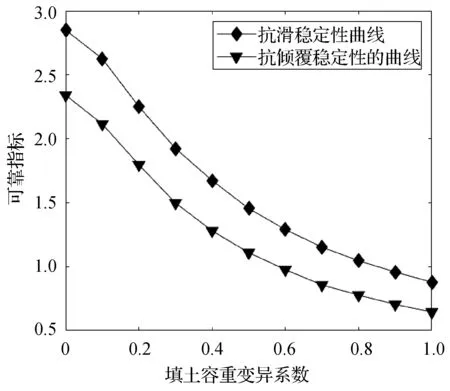
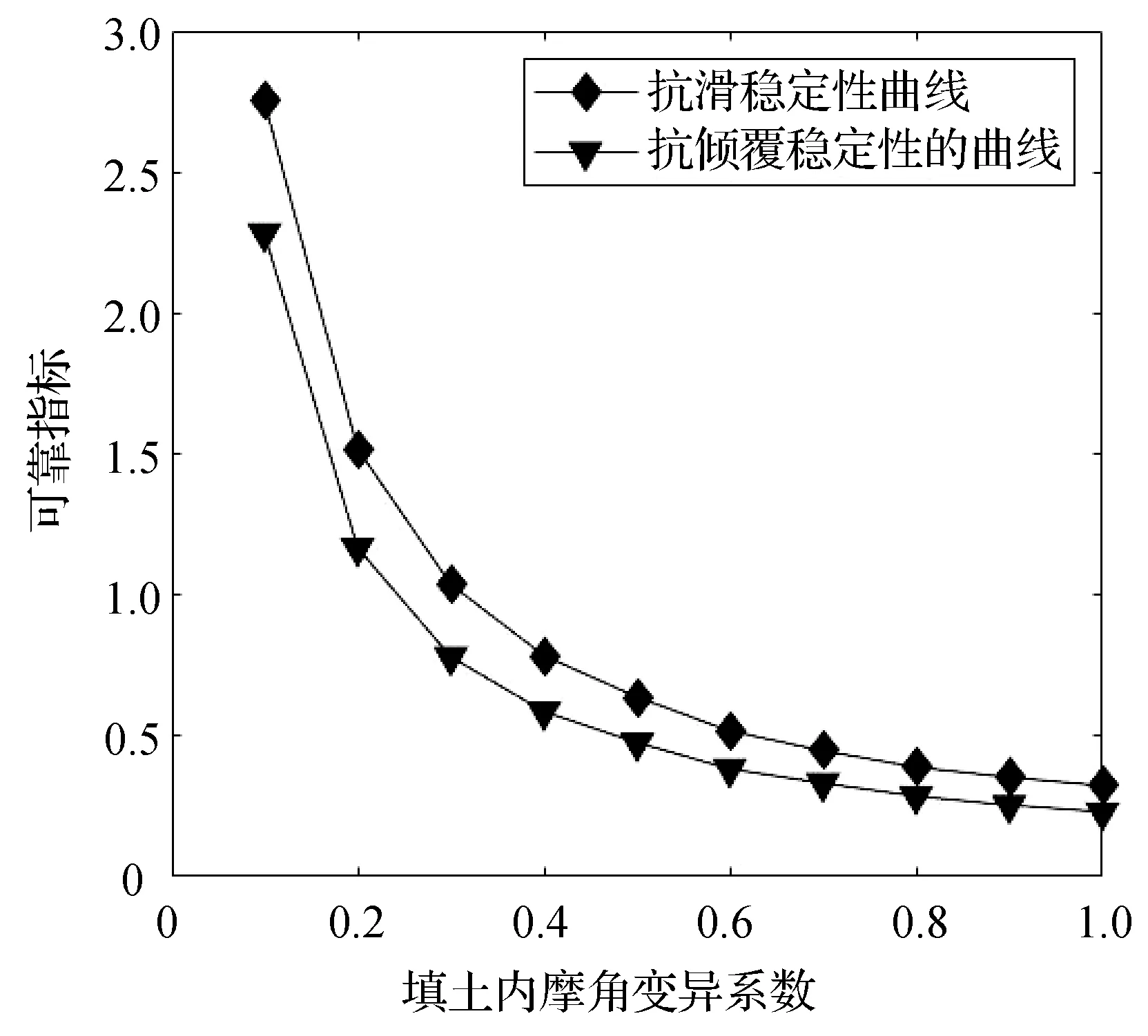
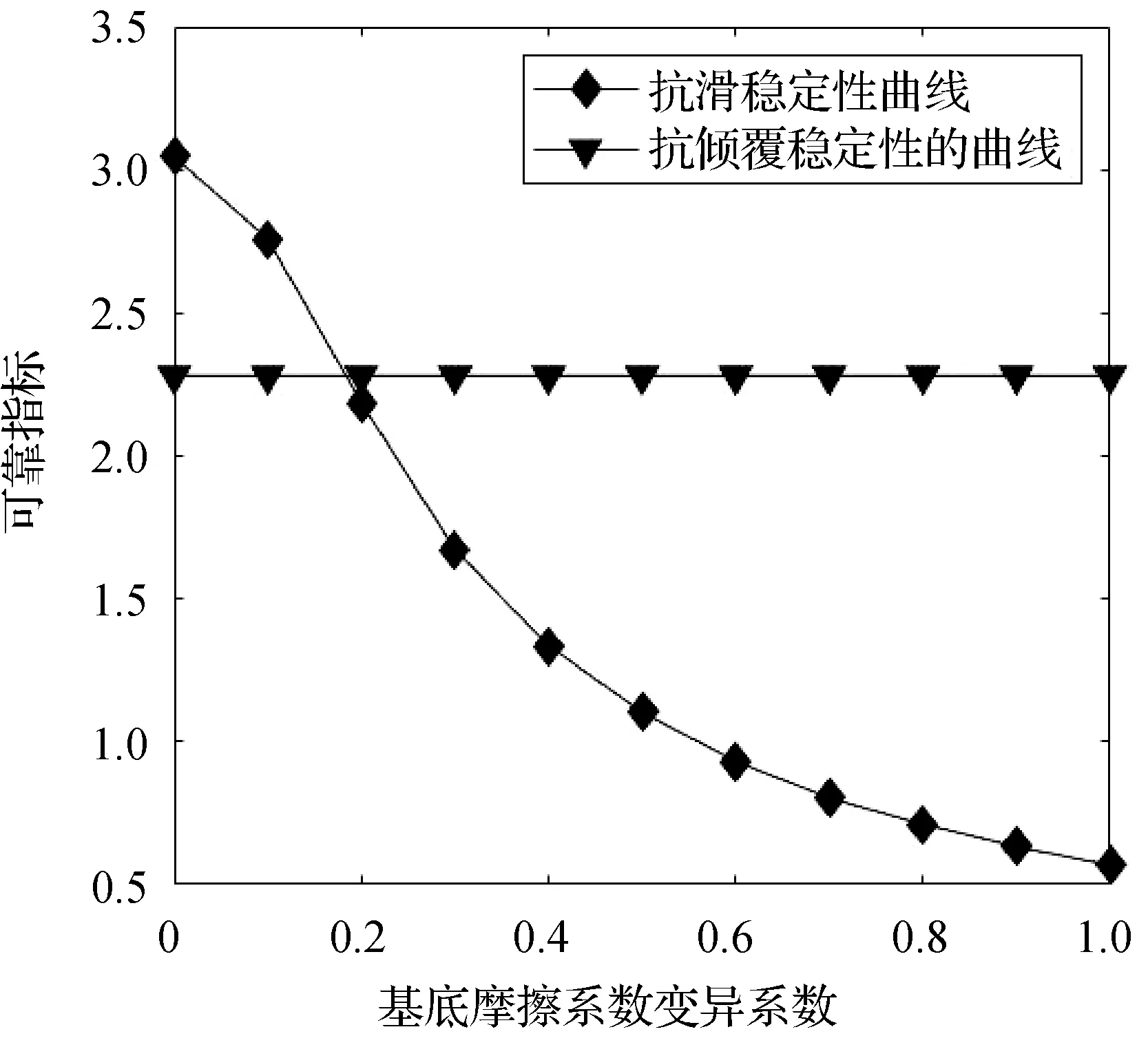
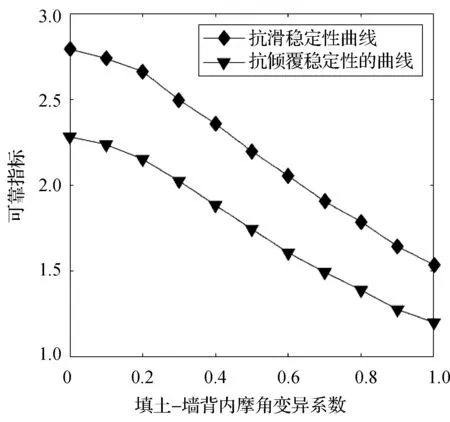
etaining.xlsx′)”实现。 使用MATLAB的Application Compiler工具箱可将GUI界面设计生成的主程序文件及关联文件编译成独立使用的安装包,安装后的.exe应用程序可以在不安装MATLAB的情况下启动主界面的计算窗口。该功能的实现是基于一套独立共享库——MATLAB Runtime来完成的。此外,主界面菜单栏(见图2)中的程序使用说明书以及输入框的提示信息可以为不熟悉该程序操作步骤的用户提供相应的帮助。 某重力式挡土墙如图4所示,挡墙各尺寸参数为:H=5.178 m,dk=0.5 m,Dk=0.98 m,hj=0.5 m,bj=0.3 m,L0=5 m,α=11.3°,墙底斜率为0.2。挡土墙填料容重23 kN/m3。 图4 重力式挡土墙计算简图 随机变量的各参数具体值见表2,假设表2中各参数均服从正态分布。 表2 各随机变量参数统计 在不计荷载的情况下,将已知参数输入计算界面,通过运行计算可得到对应的计算结果如图2所示。 为进一步验证计算程序的正确性与可行性,现将本文所开发的软件与工程上常用的理正挡墙软件就该算例的定值计算结果作对比分析,如表3所示。 表3 本文软件和已有软件计算结果对比 由表3可知,本文开发软件的定值计算结果与理正软件计算结果相仿。此外,本文软件还可以计算出结构在两种模式下的具体失效概率和可靠指标,为实际工程挡土墙结构的安全可靠性评价提供可靠理论依据。 通过点击稳定性分析按钮可以切换到对该算例的参数敏感性分析窗口,如图5所示。 图5 参数敏感性分析计算窗口 假设各参数均值不变,变异系数以设定步长变化,可得挡土墙抗倾覆与抗滑移可靠指标随各参数变异系数变化的曲线如图6-图9所示。 图6 可靠指标与容重变异系数关系 图7 可靠指标与填土内摩擦角变异系数关系 图8 可靠指标与基底摩擦系数变异系数关系 图9 可靠指标与填土和墙背间内摩角变异系数关系 在对四个主要影响因素进行敏感性分析后,由图6-图9可知:填土容重变异系数、基底摩擦系数变异系数、填土内摩擦角变异系数三者在0.4之前变化时对抗滑移稳定性的影响比较大,填土容重变异系数、填土内摩擦角变异系数两者在0.4之前变化时对抗倾覆稳定性的影响比较大,而填土与墙背间的内摩擦角变异系数则刚好相反。因此,在实际设计时,若相应参数变异系数低于0.4时,应准确统计其变异系数,方能更客观地分析结构的可靠度。 (1) 基于蒙特卡罗法,结合MATLAB软件矩阵算法、GUI界面设计等功能,开发一款重力式挡土墙结构可靠度计算及敏感性分析的计算机程序软件,弥补了重力式挡土墙结构传统定值分析法的不足,为进行挡墙结构可靠度计算提供了适用计算工具。 (2) 本文开发的程序可以计算不同类型(仰斜、俯斜、垂直、有无扩展墙趾、是否计算路面荷载)重力式挡土墙的结构可靠度。稳定性计算模块不仅可以计算挡土墙结构在两种失效模式下的失效概率和可靠指标,还可以计算出基于定值理论下抗滑移和抗倾覆安全系数。 (3) 本文软件开发生成了以计算过程和计算结果为主要内容的挡土墙结构可靠度计算书。查看计算书,可判断挡土墙设计是否符合规范要求。此外,软件将挡土墙模型图及分析曲线图也一并存储在相应的文件夹下,可供随时查看。 (4) 通过一个典型挡土墙算例的结构可靠度计算和敏感度分析,获得了随机参数取值及其变异系数范围对结构可靠性和安全性的影响规律,验证了本文开发程序软件的正确性和实用性。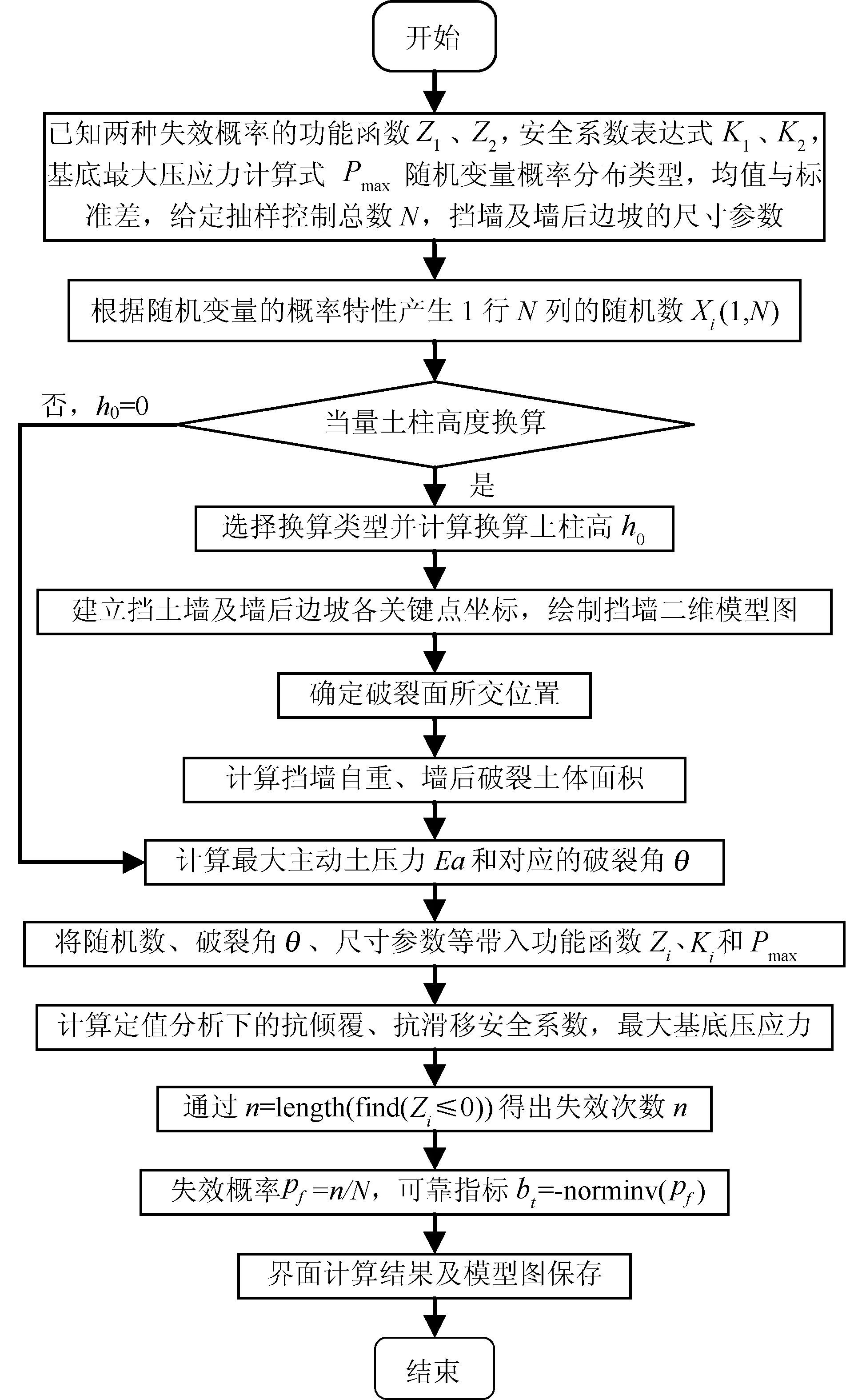
2.3 计算结果的保存与查看
2.4 应用程序构建及使用
3 程序可行性验证及敏感性分析
3.1 程序可行性验证

3.2 敏感性分析
4 结 语

