基于需求不确定性的分层网络设计研究

毛铭浩，邵荃*，于文斐

(1.南京航空航天大学民航学院，南京 211106；2.中国民航科学技术研究院，北京 100028)

随着民航业的发展，航空公司均构建起了自身的航空运输网络。而如何使得航空公司的运输网络满足其自身需求例如降低运输成本、提高运输效率，都需要对航空运输网络进行深入研究。随着航空运输网络研究的不断发展，也需要将真实世界的不确定性特点纳入研究范畴。

关于分层运输网络设计的研究，Yaman[1]提出了基于单分配模型的分层运输网络，枢纽与非枢纽之上，增加了一级中心枢纽，并考虑到服务质量，将交付时间限制纳入分层枢纽位置问题中，发现当施加时间限制时，网络总成本略有增加，中心枢纽和枢纽的数量较小时，交付时间限制的影响更强。Lin[2]研究了面向双业务的层次化轮辐网络集成设计问题，为每项业务整合了与另一业务互斥的二级航线网络，从而在满足服务时间和运营限制的情况下，将总运营成本降至最低。并设计了基于链接的隐式枚举算法，与传统的专用二级路由网络相比，该集成在每项的业务上大大降低了成本。Dukkanci等[3]提出了一个多层次的多模式枢纽网络结构，并在此网络基础上定义了一个具有服务时间限制的枢纽覆盖问题。分层网络由三层组成，其中一层是环状星形(ring-star-star, RSS)网络。每一层可能有不同类型的车辆。还开发了一种基于次梯度法的启发式求解算法，以在更合理的时间内求解问题。Khodemani-Yazdi等[4]提出了一个以枢纽设施为服务中心的双目标层次枢纽定位问题。枢纽设施分为中心设施和本地设施。设施的排队框架分别被认为是M/M/c和M/M/1。此外，关于移动时间和实体数的概率分布被假定为指数分布和泊松分布。采用一种新的博弈论变量邻域模糊杂草优化算法(game theory variable neighborhood fuzzy invasive weed optimization, GVIWO)对所建立的数学模型进行求解，算法效果优于遗传算法和模拟退火。Shang等[5]针对货物配送系统构建了层次化的多式联运轮辐配送网络，该网络涉及公路和航空两种运输方式，地面和机场两种枢纽类型，以及相应的3个层次，建立了一种基于可靠性的模糊规划模型，该模型描述了货物配送系统运行时间和处理时间的不确定性，并提出两阶段启发式算法求解。Esmizadeh 等[6]建立了多目标混合整数线性规划来建模具有互补操作的层次式枢纽网络上的冷链运输，中心枢纽在网络的第一级相互连接，并与较低级别枢纽的星形网络连接，扰动被建模为随机需求和多层次的时间窗，并提出了一种适合于大型网络竞争的遗传算法进行求解。Ghaffarinasab等[7]提出了p-hub 中心和p-hub最大覆盖问题在分层情况下的混合整数线性规划(mixed integer linear programming, MILP)模型，其中每个始末节点(origin/destination, O/D)对所对应的流量被划分为不同的层，每个层都有特定的服务水平需求，并开发了相应的Benders分解算法来求解大型实例。

关于中枢辐射网络的不确定性研究，2012年Alumur等[8]基于网络规划的长期性，以及模型输入数据的不准确性，将枢纽开设成本和O/D对流量的不确定性引入中枢辐射网络设计，分别针对单分配和多分配模型进行改进，分析了孤立的和组合的不同不确定性因素所导致的成本和网络结构的变化。Azizi等[9]提出了一个在随机需求和拥塞条件下设计轮轴辐射网络的模型，使固定成本、运输成本和拥堵成本之和最小化，枢纽被建模为空间分布的M/G/1队列，并且使用枢纽设施的预期队列长度来捕获拥塞，结果表明，如果在设计阶段就考虑到枢纽设施的拥塞，则可以通过总成本的小幅增加而大幅减少拥塞。Correia等[10]提出了一个多周期随机容量下的多分配枢纽选址问题的建模框架，将规划期划分为多个时间段，假设需求的不确定性，决策涉及枢纽的位置、其初始容量、现有枢纽的容量扩展以及出发地和目的地对之间的运输，目标是使总预期成本最小化，不确定性被有限的场景集和估计的概率表示。Hu等[11]提出了需求不确定条件下考虑枢纽容量均衡利用的单分配容量枢纽选址问题的随机模型，假设需求是独立的随机变量，具有已知的正态概率分布，建立了具有联合机会约束的随机规划模型，并将其转化为二阶混合整数规划模型，结果表明：只需小幅提高传统的运行成本，就可以大大降低枢纽容量的整体不平衡利用率。Rahmati等[12]针对需求不确定、稳定性水平受不确定性预算控制的无承载枢纽选址问题，提出了一种两阶段鲁棒优化方法，第一阶段确定枢纽设施的选址，第二阶段确定枢纽设施的分配，采用加速Benders分解算法求解该问题，计算实验表明，所提方法在迭代次数和计算时间方面都有较好的表现。Sener等[13]研究了松弛确定性运输成本和需求假设的多分配枢纽覆盖问题，使用L-Shaped算法，根据仿真数据生成并求解了几个测试实例，结果表明：与期望值法的期望相比，将轮毂覆盖问题建模为随机优化模型的效率提高了13.05%。

目前分层网络研究主要集中于地对分层运输网络理论建模，以及在基础模型上更多地纳入现实运输网络的特点。不确定性研究主要针对需求(O/D流量)、运输成本、枢纽开设成本等。然而，在以往研究中，考虑不确定性时总是在经典的单分配和多分配模型上进行改进，而缺少对新的航空运输网络类型进行不确定性分析。

为此，结合现有分层航空运输网络研究和不确定性理论，以文献[1]的确定型分层运输网络模型为主干，使用文献[8]将需求不确定性引入单分配和多分配中枢辐射网络模型时的思想，设置需求场景集合包含多种可能的需求场景，优化需求场景集合下网络运输成本的数学期望最小。以此为基础提出基于需求不确定性的分层运输网络设计模型，同时给出网络中O/D路由的求解方法。然后以某年中国的实际航空运输数据为例，针对需求确定型分层运输网络、期望需求表征不确定性的分层运输网络和不确定型分层运输网络，对比它们在4种需求情景下的运输成本表现情况，计算分析所提出的分层运输网络模型成本在需求不确定影响下的成本鲁棒性、最大运输距离和枢纽拥堵水平方面的表现。

1 基于需求不确定性的分层网络设计模型

1.1 问题描述

分层运输网络设计属于网络枢纽选址问题，在分层运输网络中，节点分为出发地/目的地(O/D)节点，枢纽节点，中央枢纽节点。边包括非枢纽与枢纽，枢纽与中央枢纽，中央枢纽之间的连接。分层运输网络设计问题即是给定n个离散的节点位置，两两节点对之间形成O/D对，O/D对之间有运输需求(流量)和单位流量运输成本。从n个节点中选出h个枢纽，从h个枢纽中选出h0个中央枢纽，然后将h-h0个枢纽分配给h0个中央枢纽，将n-h个枢纽分配给h个枢纽，实现总网络运输成本最小。

但由于航线网络规划的长期性，以及模型输入数据的不准确性，需要将需求(流量)的不确定性引入分层网络设计，以提高分层运输网络对抗不确定性扰动的能力，表现为在多种可能的需求情况下，所得出运输网络的运输成本与各需求场景最小运输成本的平均差值最小。

1.2 模型建立

以文献[1]的确定型分层网络运输模型为主干，使用文献[8]改进单分配和多分配中枢辐射网络模型的思路建立分层运输网络模型。

(1)模型假设如下。①中央枢纽间完全互联，单一连接；②非枢纽之间，枢纽之间不直接交互；③非枢纽-枢纽，枢纽-中央枢纽，中央枢纽之间的运行成本有折扣因子；④运输成本满足三角不等式。

(2)集合。设I为网络节点集合，H⊆I为可能的枢纽节点集合，C⊆H为可能的中央枢纽节点集合，S为不确定性需求(流量)场景集合。

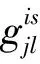
基于需求不确定性的分层运输网络数学模型如下。

(1)

(2)

zijl≤zjjl, ∀i∈I；j∈H{i}；l∈C

(3)

(4)

(5)

(6)

(7)

(8)

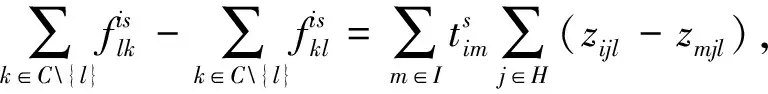
∀i∈I,l∈C,s∈S

(9)

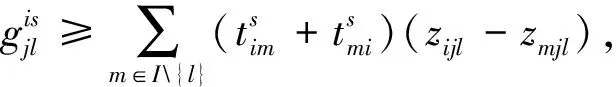
∀i∈I,j∈H,l∈C{j},s∈S

(10)

zljl=0, ∀j∈H,l∈C{j}

(11)

(12)

(13)

zijl∈{0,1}, ∀i∈I,j∈H,l∈C

(14)

(1)目标函数。式(1)求场景集合S下，网络总成本的数学期望，网络总成本包括非枢纽-枢纽、枢纽-中心枢纽、中心枢纽之间的运输成本。

(2)网络结构约束。式(2)约束表示对于∀i∈I，非枢纽节点只能分配给一个枢纽和一个中央枢纽。式(3)约束非枢纽节点的分配条件，i∈I分配给j∈H时，要求j为枢纽。式(4)约束枢纽的分配条件，j∈H分配给l∈C时，要求l为中央枢纽。式(5)表示中央枢纽至少被一个枢纽连接。式(6)表示枢纽至少被一个非枢纽连接。式(7)约束枢纽的数量为h。式(8)约束中央枢纽的数量为h0。

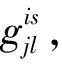
(4)变量特征约束。式(11)非必要，但可以减少计算时的变量数量、松弛问题。式(12)和式(13)是变量的非负约束，式(14)约束分配示性因子为0-1变量。

分配示性因子zijl只表征非枢纽-枢纽-中央枢纽的分配情况，分层运输网络模型的O/D路由求解方法为：已知分层运输网络的节点分配，设节点i的分配为(i,ji,li)，节点m的分配为(m,jm,lm)，括号内元素依次为非枢纽节点、枢纽、中央枢纽。①若ji=jm=j，必有li=lm=l，则O/D路由为i-j-m；②若ji≠jm，且li=lm=l，则O/D路由为i-ji-l-jm-m；③若ji≠jm，且li≠lm，则O/D路由为i-ji-lj-lm-jm-m。

2 实例计算及结果分析

2.1 计算数据及参数设置

使用文献[14]中2012年中国15个主要城市的航空运输数据进行计算，包括城市对的运输需求(O/D流)，城市对的运输成本。计算结果中城市的代表序号如表1所示。

表1 城市的代表序号

设置可能的枢纽节点集合、可能的中央枢纽节点集合与网络节点集合相同，即I=H=C。设置常量αH=0.9，αC=0.8，h=5，h0=2。

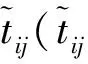
对3种分层网络设计方法进行计算比较：①方法一，需求确定，使用确定型分层网络模型进行计算；②方法二，需求不确定，先计算场景集合需求的数学期望以表征不确定性，然后使用确定型分层网络模型进行计算；③方法三，需求不确定，使用本文模型计算。

通过Lingo18.0求解3种网络设计方法的非枢纽-枢纽-中央枢纽分配情况，以及4种需求场景下的最佳网络运输成本，然后将3种网络设计方法的分配方式应用于4种需求场景。计算分析3种方法所得的分层运输网络在3个方面的特性。

(1)网络运输成本的鲁棒性。文献[8]将成本鲁棒性定义为所采取方案得到的成本与可能情景下最优成本之间差值的平均值。因此，采用每种方法在4种需求场景下的可得成本与最优成本之间差值的平均值代表每种方法的鲁棒性。

(2)最大运输距离。当航空器速度一定、不考虑机场内转运时间的情况下，航空运输距离可代表航空运输时间，航空运输作为一种服务产品，航空运输时间与服务质量相关。通过所提出的分层运输网络O/D路由求解方法，累加O/D流在分层运输网络中的各段运输距离，计算O/D城市对之间最大运输距离。

(3)拥堵水平。根据文献[15]，枢纽的拥堵水平可表示为

f(u)=aub

(15)

式(15)中：u为枢纽的流量；a、b为正的常量，且b≥1，当a=b=1，通过枢纽的流量就表示枢纽的拥堵水平。

通过所提出的分层运输网络O/D路由求解方法，计算O/D路由，确定汇入各枢纽的流量，然后设置a=b=1，用式(15)计算各枢纽的拥堵水平然后求平均，得出分层运输网络的平均枢纽拥堵水平。

2.2 计算分析

首先，计算3种方法的分层网络结构如表2所示。

表2 3种方法的分配结果

由表3可知，①中央枢纽的选择方面：3种方法所得的枢纽分配方案都将中央枢纽选在15个城市中相对靠中心位置的长沙、南京、郑州3个城市，这表明为便于协助周边区域的枢纽完成转运，中央枢

纽会分布于机场群中相对靠中心的位置；②枢纽的选择方面：由于未考虑政策、民航产业发展情况、机场中转能力等因素，实际的枢纽北京、上海、广州由于地理区位过于靠北、靠东、靠南，因此只作为第二级的枢纽而未能成为中央枢纽，这表明第二级枢纽承担非枢纽和中央枢纽的沟通，大多分布于机场群边缘区域的中心；③非枢纽的连接方面：仍有很多非枢纽节点直接连接中央枢纽，这表明若枢纽-中央枢纽、中央枢纽之间运输的折扣因子未能有效减少成本，则模型在分配非枢纽时，会使得非枢纽节点直接连接中央枢纽，通过减少转运次数和运输距离，从而降低运输成本。

然后，使用确定型枢纽网络模型计算4种场景的最小运输成本。根据所提出的OD路由计算方法，得到方法一、方法二和方法三的城市OD对路由，然后计算应用方法一、方法二和方法三时4种场景的运输成本，如表3所示。

由表3可知：①场景1的最小运输成本与使用方法一时相同，其原因为方法一是使用原数据计算得到的确定型分层网络结构方案，场景1的需求数据与原数据相同，计算结果相同；②场景2的最小运输成本与使用方法三时相同，场景3的最小运输成本与使用方法二时相同，其原因为虽然方法二和方法三都融入了不确定因素考量，但是算例中城市数量较少，能实现较小网络运输成本的分层网络结构较为有限，不同方法产生的网络结构形成重叠。若是选取被广泛运用于航线网络设计问题算例的包含美国25个城市的CAB数据库，则一般能避免此情况的发生。

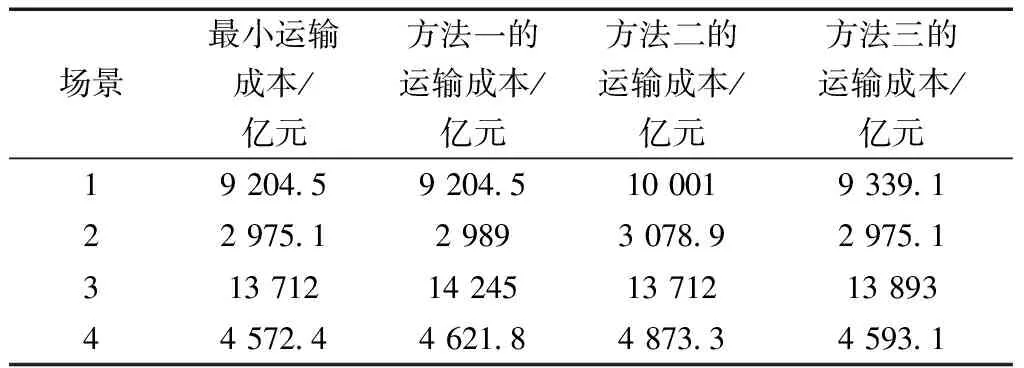
表3 4种场景在3种方法下的运输成本

计算4种场景的最小运输成本与3种方法下的运输成本差值如表4和图1所示。

结合表4和图1可得，方法三与4种场景最小运输成本的平均差值最小，方法二与4种场景最小运输成本的平均差值最大。这表明在面对可能发生的多种需求情景时，直接采用确定型分层网络运输模型或是直接使用可能需求情景的数学期望来带入计算并不能很好地处理需求不确定性对成本

图1 运输成本差值

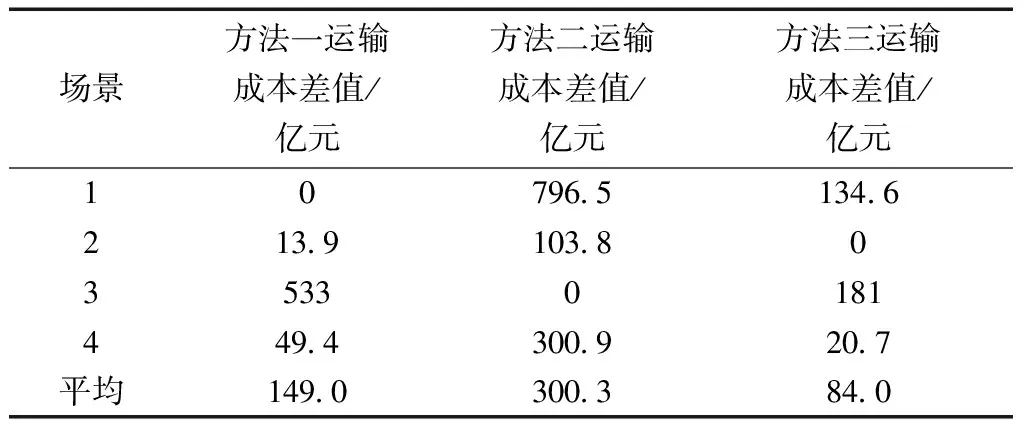
表4 运输成本差值

的影响。而本文提出的基于需求不确定性的分层网络鲁棒设计模型给出的方案在面对多种可能的需求情景下，与各场景最优运输成本的平均差值最小，具有较好的成本鲁棒性。

求解3种方法所得网络结构的O/D路由，累加O/D对之间在分层运输网络中的各段运输距离，计算3种方法所得的分层运输网络最大运输距离如图2所示。

在3种方法中，最大运输距离都出现在乌鲁木齐—沈阳的运输路径上。由图2可知，所提出的模型方法三的最大运输距离最长。因为目标函数是针对网络总运行成本，而且约束条件也未兼顾到运输距离/运输时间。未来的研究可在本文模型的基础上添加运输距离约束，或者将该问题设置为运输成本和运输距离最小的多目标优化问题，从而降低运输距离和运输时间。

图2 最大运输距离

计算O/D路由，确定汇入各枢纽的流量，计算各枢纽的拥堵水平然后求平均值，3种方法所得的分层运输网络中平均枢纽拥堵水平如图3所示。

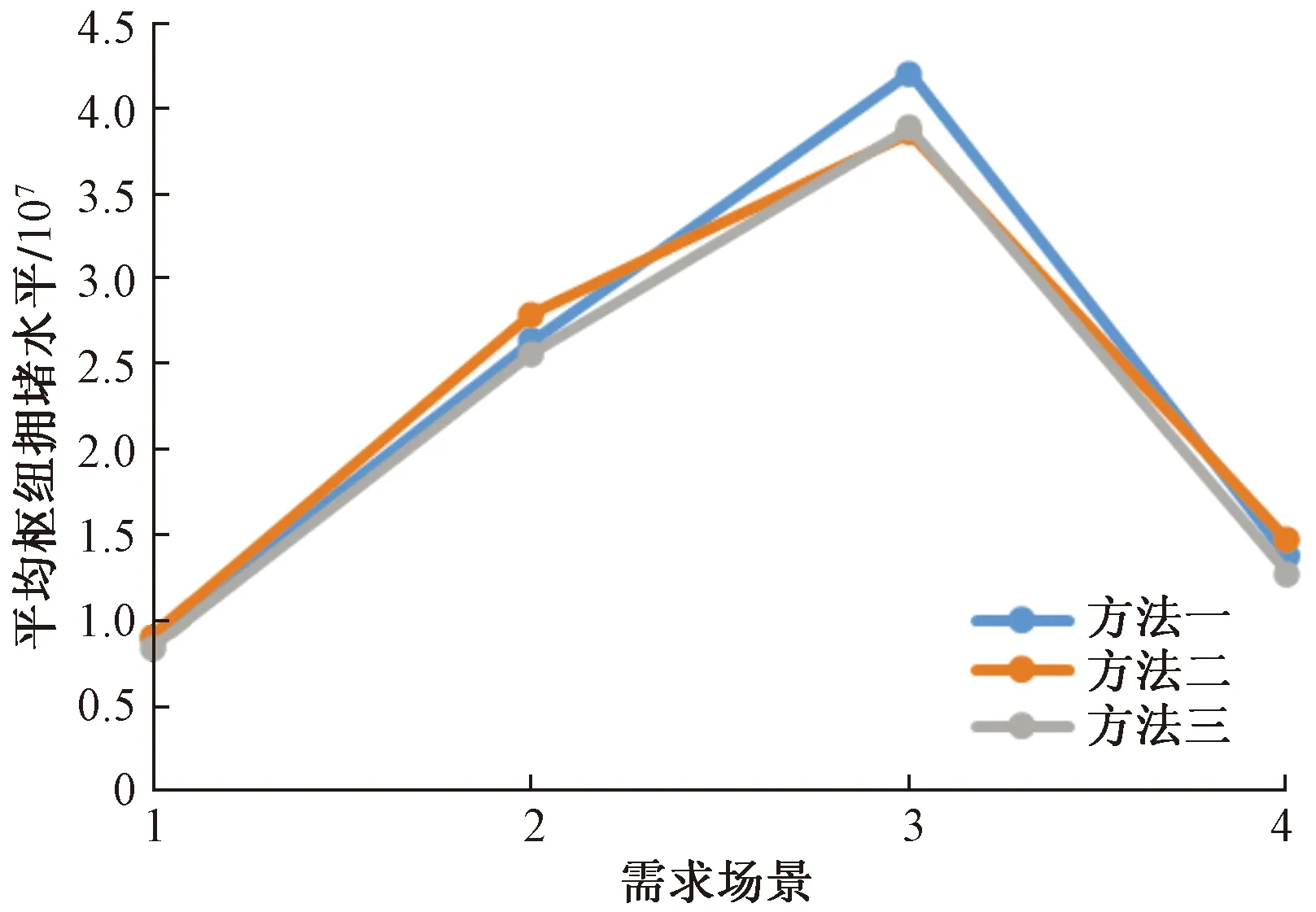
图3 平均枢纽拥堵水平

由图3可知，方法三的平均枢纽流量除场景3外总是小于方法一和方法二，表示方法三有着最低的平均枢纽拥堵水平。虽然本文目标函数的含义为求多种需求(流量)场景下的网络运行成本期望最小，并未专门针对平衡流量降低拥堵而进行的网络结构优化配置，但是从结构上对比3种方法所得的分层运输网络枢纽和非枢纽的分布特征可以发现，本文模型所得的网络结构中，各个枢纽、中央枢纽所连非枢纽节点的数量恰好相同，非枢纽节点在枢纽节点的末端分布较为平均，因此能够得到较低的平均枢纽拥堵水平。

3 结论

结合现有分层航空运输网络模型研究和不确定性理论，以确定型分层网络运输模型为主干，建立需求集合包含多种可能的需求场景，将优化目标设置为需求场景集合下运输成本期望最小。提出基于需求不确定性的分层网络设计模型，同时给出网络中O/D路由的求解方法。然后以某年中国城市的实际航空运输数据为例，针对需求确定型分层运输网络、需求期望表征不确定性的分层运输网络和不确定型分层运输网络，对比它们在均匀分布产生的需求情景集合下的运输成本表现情况，以衡量不同分层运输网络设计模型在需求不确定影响下的成本鲁棒性表现。计算结果表明，所提出的基于需求不确定性的分层运输网络鲁棒设计模型与各需求场景最小运输成本的平均差值最小，表明在面对多种可能的需求情景下仍能表现出较小的网络运输成本，具有较好的成本鲁棒性。研究工作可为航空运输企业在面对需求不确定环境下的运输网络设计方面提供参考。