飞机在牵引转弯工况下的运动轨迹仿真与分析

于鸿彬，赵嘉伟

(天津工业大学机械工程学院，天津 300387)

牵引安全是整个民航安全的重要环节，飞机牵引车是机场用于移动飞机的地面保障设备和救援设备，目前中国开通机场约260个，相关特种车辆65 000台[1]，中外机场每年都会发生多起飞机在地面牵引转弯过程中与其他飞机、设备或廊桥磕碰的事故，造成大量财产损失[2]。

相关飞机牵引的安全性研究较多，文献[3]建立了有杆飞机牵引系统的动力学模型，分析了路面凹凸、意外制动等工况下飞机前起落架及牵引杆的受力情况，进而对飞机牵引安全规范提出了建议。文献[4]通过建立飞机前起落架的有限元模型、粘贴应变片及全桥电路的优化布置为检测前起落架牵引力提供了新思路。文献[5]对高速牵引工况中前起落架结构的振动特性进行了模拟研究，为起落架的设计提供参考。文献[6]建立了轮毂电机驱动的飞机牵引系统非线性模型，利用准滑模控制实现飞机偏航稳定控制。文献[7-8]通过建立舰载机与牵引车的运动模型，分别利用RRT(rapidly-exploring random trees)算法和LOS(line of sight)算法对牵引车路径规划和轨迹跟踪进行了研究，为牵引车无人化和智能化提供了可能。目前，相关研究多集中于牵引过程中前起落架的力学特性研究和新型牵引车的稳定性控制及轨迹规划研究，忽略了对传统牵引系统在转弯工况中轨迹特性研究和牵引车自身结构参数对飞机轨迹的影响。由于飞机机身较长，机体较大，在牵引过程中很难及时掌握飞机相对于牵引车的轨迹动态，且传统牵引车成本低、适应性强、设备保有量大，在短时间内不会被新型牵引车淘汰，因此对传统飞机牵引系统的轨迹特性研究很有必要。

根据作业方式不同，牵引车主要分为有杆式飞机牵引车和无杆式飞机牵引车。无杆式飞机牵引车具有自重小，作业半径较小以及牵引效率高等优点，是牵引车未来发展的趋势[9-10]。因此，基于传统无杆式飞机牵引车建立了飞机牵引系统的运动学模型，通过迭代计算的方法模拟了飞机牵引系统在转弯工况下的轨迹和飞机前轮转角情况；同时由于不同厂家牵引车结构参数各异，在现有模型的基础上以轨迹偏差和飞机前轮转角为指标分析了牵引车不同结构参数对飞机转弯性能优劣的影响，为牵引车设计生产提供参考。

1 飞机牵引系统的运动学建模

假定飞机牵引系统在同一平面上低速运行，为便于对其运动性能进行研究，忽略轮胎侧偏、摩擦和地面坡度等因素，将牵引车与飞机主起落架左右车轮集中于牵引车与飞机中轴线上，形成牵引车和飞机的单轨模型[11]，如图1所示。假设AB、CD为两根不计质量的刚性杆，其中A点为牵引车前轴的中点，B点为牵引车后轴的中点，C点为飞机牵引车的抱轮机构，D点为飞机主起落架连线的中点，D点为受控点，其位置与运动方向受A、B点及飞机前轮转角决定。

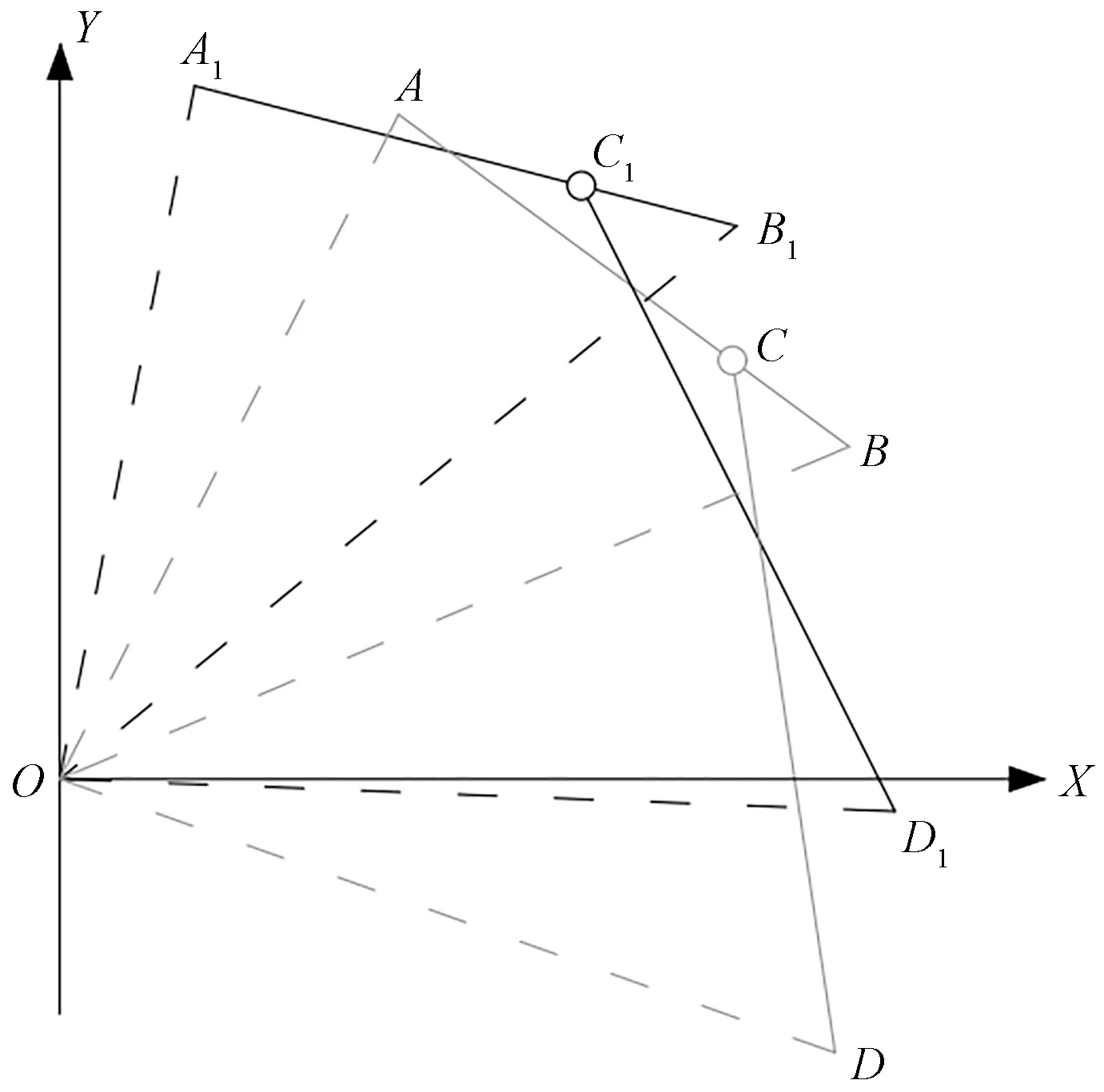
图1 飞机—牵引车运动学模型

采用PRT法(直角坐标-极坐标-切线法)对飞机牵引系统进行建模，以O点为原点建立直角坐标系，X轴为横轴，Y轴为纵轴，同时以O点为极点建立极坐标系，并规定OX为极轴。因此可以导出A点、B点、C点、D点的直角坐标和极径依次为(x1，y1)、(x2，y2)、(x3，y3)、(x4，y4)和OA(OA1)、OB(OB1)、OC(OC1)、OD(OD1)，A1点、B1点、C1点、D1点分别为A点、B点、C点、D点在下一时刻的位置，C点、D点随B点极径和极角的变化而变化。通过预设步长并迭代的方法，可依次得到各点在转弯工况下每一时刻的位置，迭代完成后即可求得飞机牵引系统在牵引转弯工况下的运动轨迹。

2 飞机牵引系统各点轨迹求解

2.1 B1点坐标表达式求解

根据图1中几何关系，当飞机牵引系统在极短时间内，由ABCD运动到A1B1C1D1位置状态时有

(1)

根据极限定义，有

(2)

即

(3)

式(3)为一阶线性微分方程的形式，可得其通解为

(4)

式(4)中：C为不定常数。

当步长趋于无穷小时，∠OBB1≈∠ABO,故视其为常量，为了方便计算并确定不定常数，式(4)可改写为

(5)

B1点坐标表达式为

(6)

2.2 A1点坐标表达式求解

A点为飞机牵引车前轴的中点，代表飞机牵引系统的前进方向，设A点在牵引系统转弯工况下的转弯半径为R，当A点沿圆周运动时，A点的极径为OA1=OA=R，根据几何关系，有

(7)

∠A1OX=∠A1OB1+∠B1OX

(8)

A1点坐标表达式为

(9)

当牵引系统从A1(0，R)出发，分别以90°和180°驶出弯道时，A1点的终点坐标分别为

(10)

(11)

式中：R为转弯半径。

2.3 C1点坐标表达式求解

根据几何关系，有

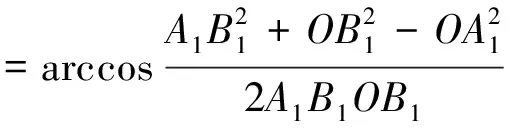
(12)

(13)

(14)

∠C1OX=∠B1OC1+∠B1OX

(15)

C1点坐标表达式为

(16)

2.4 D1点坐标表达式求解

根据几何关系，有

∠C1OD=∠C1OX+∠DOX

(17)

(18)

(19)

∠C1DC=∠CDO-∠C1DO

(20)

(21)

联立式(17)～式(21)可得

(22)

(23)

∠D1OX=∠DOX+∠D1OD

(24)

D1点坐标表达式为

(25)

(26)

式(26)中：∠C1D1O替代下一个步长[式(19)]中的∠C1DO。

2.5 飞机前轮转角的计算

在牵引过程中，飞机前轮转角大小及变化幅度影响着飞机在地面牵引过程中机身及起落架的稳定性与安全性，不同型号飞机在牵引转弯工况下前轮转角的最大值不同，在飞机牵引过程中应尽量减小前轮转角的大小及变化幅度[12]。如图2所示，α1为大地坐标系XOY与牵引车坐标系X1BY1的夹角，α2为大地坐标系XOY与飞机坐标系X2DY2的夹角，θ1为飞机与牵引车所夹锐角，同时也为飞机前轮转角。

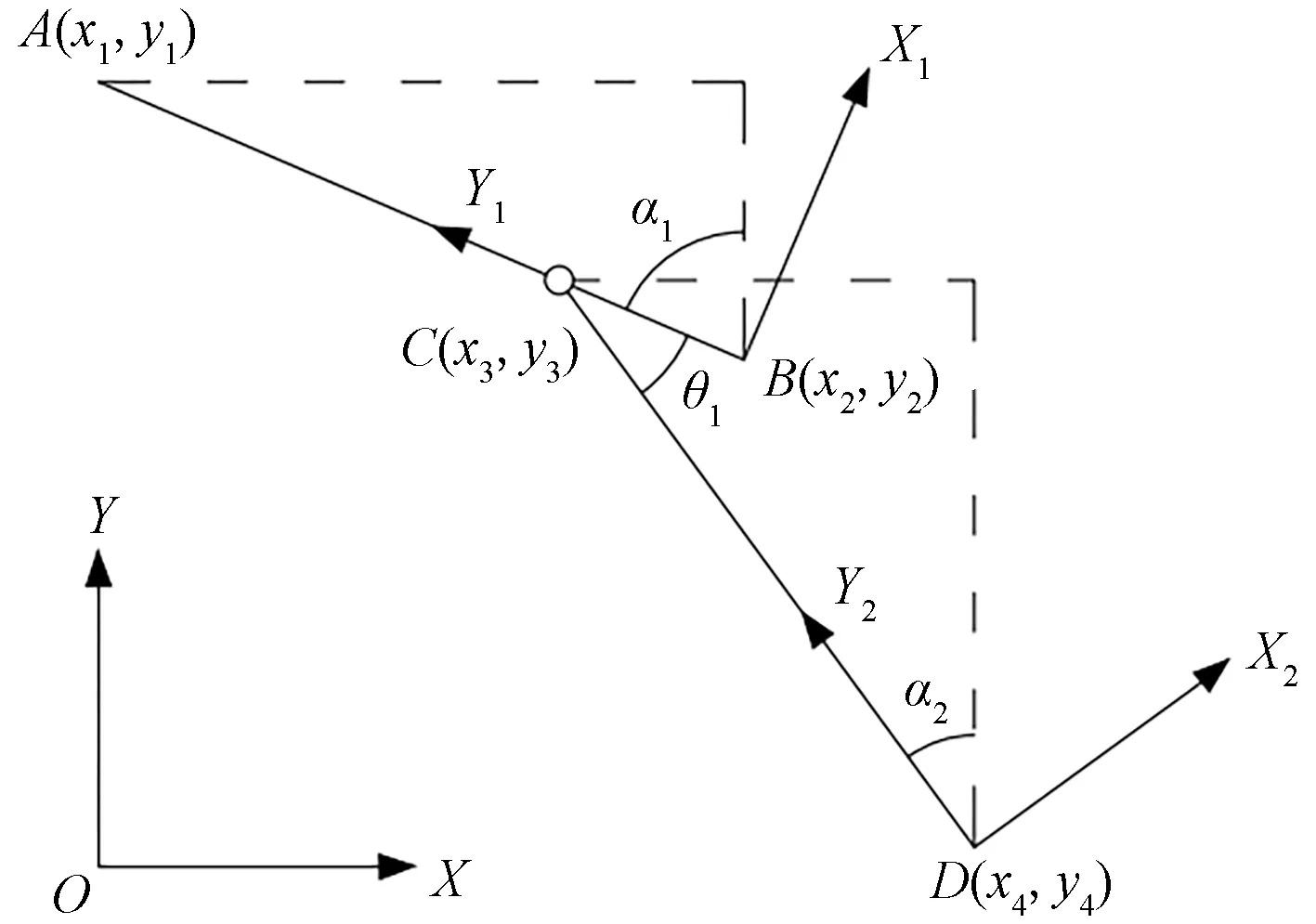
图2 飞机前轮转角计算分析图

根据几何关系，计算过程有

(27)

(28)

θ1=arcsin[sin(α1-α2)]

(29)

2.6 飞机牵引最小转弯半径的计算

飞机牵引系统与单个车辆或飞机的转弯过程不同，要研究飞机牵引系统在转弯工况中的运动轨迹特性并分析不同牵引车参数对飞机轨迹的影响，首先要计算飞机牵引系统的最小转弯半径[13],在最小转弯半径下进行对比分析。

图3为飞机在最小转弯半径下的运动简图。C点为飞机前轮，D点为飞机主起落架连线的中点，飞机在牵引转弯过程中，后轮作纯滚动，V1为C点速度方向，V2为D点速度方向。以波音737-800为例，飞机在地面牵引过程中前轮最大转角为78°，此时过C点作垂直于V1的垂线交主起落架连线的延长线于O1点，O1点即为飞机牵引系统的速度瞬心，同时也为牵引系统的旋转中心，O1C即为飞机牵引系统的最小转弯半径。

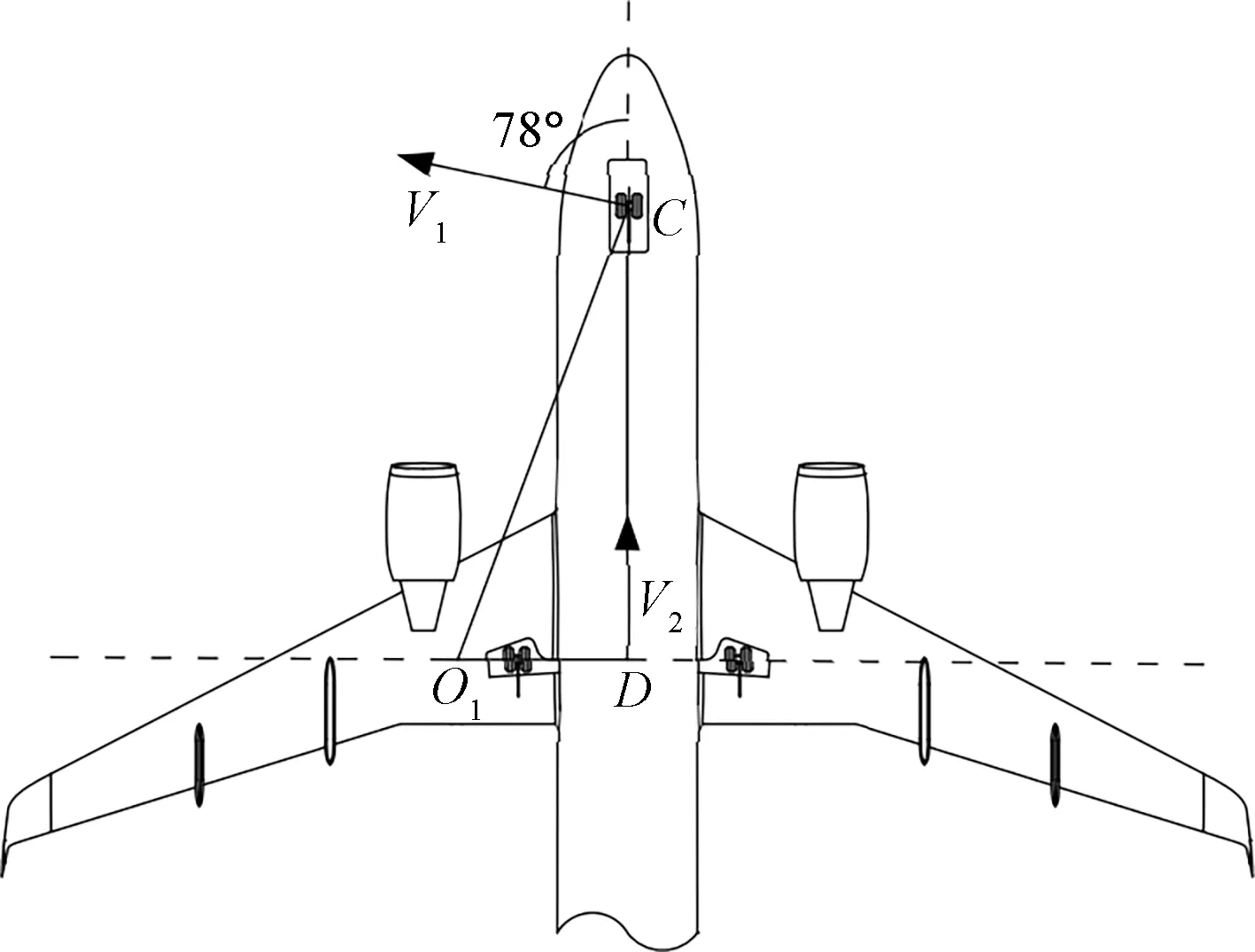
图3 飞机牵引系统最小转弯半径简图

根据几何关系，计算过程有

(30)

式(30)中：Rmin为最小转弯半径。

已知CD=15.6 m，得O1C≈15.95 m。

3 飞机轨迹建模与分析

3.1 不同路径下飞机牵引系统的弯道轨迹建模结果

初始研究对象的具体结构参数如表1所示。以波音737-800飞机和Goldhofer F396P牵引车作为初始研究对象进行建模[14]，以R=15.95 m为转弯半径，(15.95，0)为A点起点，在90°和180°两种常见的弯路工况下进行对比分析，得到飞机牵引系统在两种工况下的运动轨迹和飞机前轮转角变化情况，结果如图4所示。

图4 飞机牵引系统的运动轨迹和飞机前轮转角变化情况

表1 初始结构参数

在牵引转弯工况中，飞机与牵引车存在较大的轨迹偏差，从直道进入弯道过程中，B点、D点向内侧偏移，偏移量逐渐增大，飞机前轮转角的变化幅度较小；当牵引系统从弯道进入直道过程中，B点、D点向外侧偏移，偏移量逐渐减小，飞机前轮转角的变化幅度较大，同时在驶入和驶出弯道时，D点轨迹半径均小于A点的轨迹半径。

3.2 不同牵引车结构参数对飞机牵引转弯工况中的轨迹影响

3.2.1 牵引车轴距对飞机的影响

在牵引车原始结构参数的情况下增大和减小轴距进行对比分析。牵引车轴距AB的参数变化如表2所示，具体结果如图5所示。

表2 牵引车轴距变化参数

以90°圆周运动为例，如图5所示，牵引车轴距参数变化不会改变飞机牵引系统在转弯工况中的基本轨迹规律，当牵引车轴距增大时，B点、D点轨迹向弯道内侧偏移，轨迹半径减小，飞机前轮转角的变化幅度减小；当牵引车轴距减小时，B点、D点轨迹向弯道外侧偏移，轨迹半径增大，飞机前轮转角的变化幅度增大。通过以上轨迹及前轮转角的变化结果表明，选用大轴距牵引车牵引飞机转弯时，飞机的转弯半径较小，机身及起落架稳定性较高，但飞机对于牵引车的跟随性降低；选用小轴距牵引车牵引飞机转弯时，飞机的转弯半径较大，机身及起落架稳定性较差，但飞机对于牵引车的跟随性提高，及提高了牵引系统的通过性。

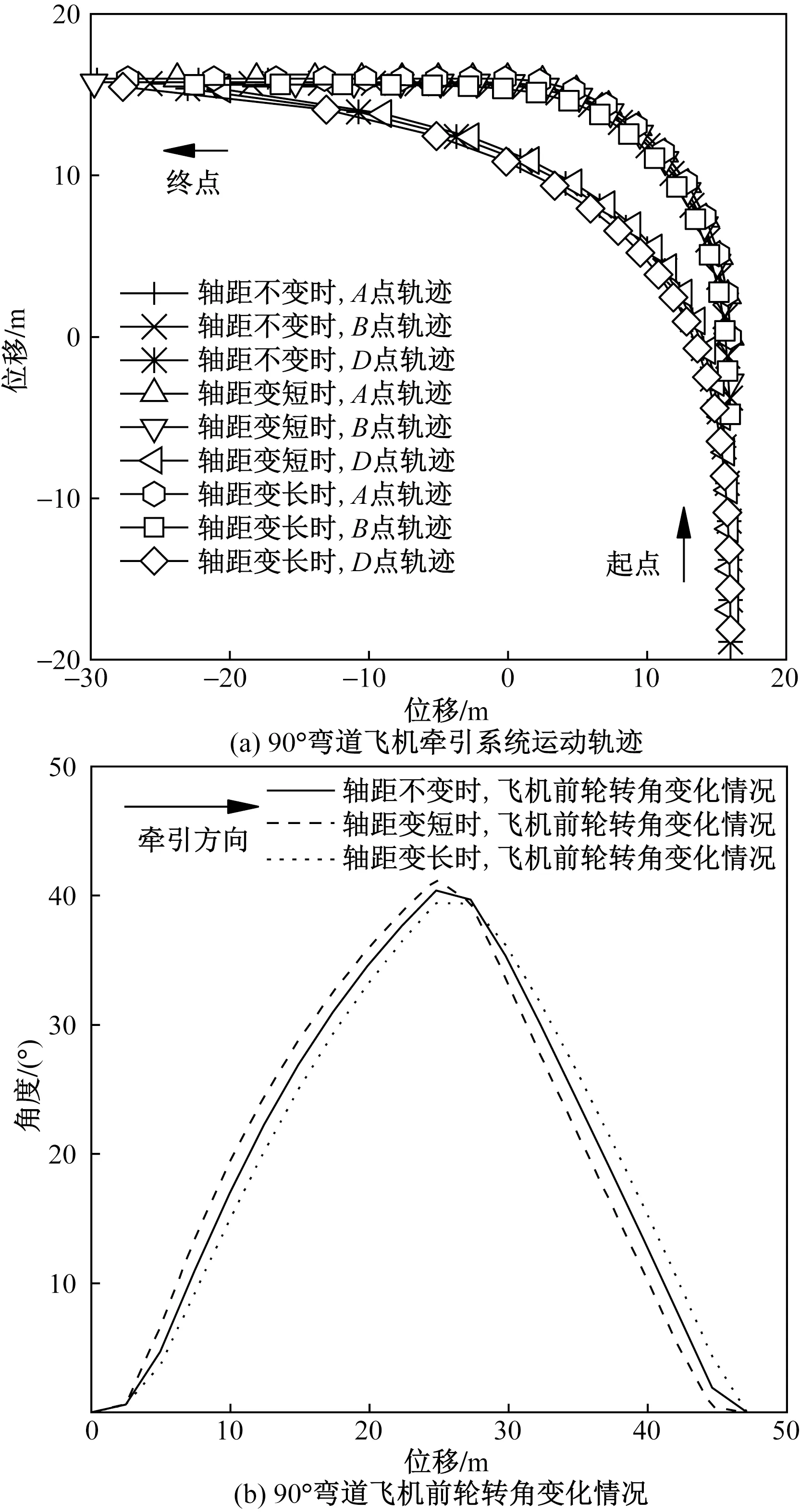
图5 轴距不同时飞机牵引系统运动轨迹和飞机前轮转角变化情况

3.2.2 牵引车抱轮机构位置对飞机的影响

在牵引车原始结构参数的情况下前移和后移抱轮机构位置进行对比分析。抱轮机构位置变化参数如表3所示，具体结果如图6所示。

表3 牵引车抱轮机构位置变化参数

图6 抱轮机构位置不同时飞机牵引系统运动轨迹和飞机前轮转角变化情况

以90°圆周运动为例，如图6所示，A点和B点在抱轮机构位置不同的情况下运动轨迹相同。当抱轮机构位置前移时，D点轨迹半径略微增大，飞机前轮转角变化幅度减小；当抱轮机构位置后移时，D点轨迹半径略微减小，飞机前轮转角变化幅度增大。通过以上运动轨迹及飞机前轮转角的变化结果表明，牵引车抱轮机构位置对于飞机在牵引转弯工况中的运动轨迹基本无影响。当抱轮机构位置距离牵引车后轴越短，机身及起落架的稳定性越低，反之，当抱轮机构位置距离牵引车后轴越长，机身及起落架在牵引转弯工况中的稳定性越高。

4 结论

合理简化了飞机—牵引车系统，采用PRT法构建了飞机牵引车系统在牵引转弯工况中的运动学模型，运用几何定理求解，得到其运动轨迹特性及前轮转角变化情况。得出如下结论。

(1)在牵引转弯工况中，飞机后轮与牵引车前后轮存在较大的轨迹偏差，在驶出弯道时，由于飞机前轮转角幅度增大，驾驶员应注意车速及周围环境以提高飞机牵引系统的安全性。

(2)牵引车轴距和抱轮机构位置对飞机运动轨迹及前轮转角变化情况会产生影响：在牵引工作中，较大轴距的牵引车在执行牵引工作时可提高机身及起落架的稳定性。较小轴距的牵引车在执行牵引工作时可提高飞机的过弯能力。抱轮机构位置对于飞机在转弯工况下的运动轨迹基本无影响，但抱轮机构相对于牵引车后轴距离较大时，可提高机身及起落架在牵引转弯工况中的稳定性。

(3)只在运动学角度对飞机牵引系统进行了研究，反映了一定运动规律，但忽略了一些因素，在后续研究中需要进一步深入讨论和验证。